2022年高考湖南卷力学计算题探析
2023-03-20湖北省监利市实验高级中学黄尚鹏
■湖北省监利市实验高级中学 黄尚鹏
2022年高考湖南卷第14题以拍篮球为情景,综合考查动能定理、变力做功、动量定理等主干知识,是一道典型的动量与能量结合的力学综合题。这道题(1)(2)问的难度不大,直接利用物理规律列式求解即可,(3)问需要利用递推法推导出数列的通项公式,运用数学知识求解物理问题。下面深入探究这道力学计算题的求解方法,供同学们参考。
一、对高考原题的分析与解答
题目:如图1甲所示,质量为m的篮球从离地H高度处由静止下落,与地面发生一次非弹性碰撞后反弹至离地h的最高处。设篮球在运动过程中所受空气阻力的大小是篮球所受重力的λ倍(λ为常数,且0<λ<且篮球每次与地面碰撞的碰后速率与碰前速率之比相同,重力加速度大小为g。
(1)求篮球与地面碰撞的碰后速率与碰前速率之比。
(2)若篮球反弹至离地h的最高处时,运动员对篮球施加一个向下的压力F,使得篮球与地面碰撞一次后恰好反弹至离地h的高度处,力F随高度y的变化如图1乙所示,其中h0已知,求F0的大小。
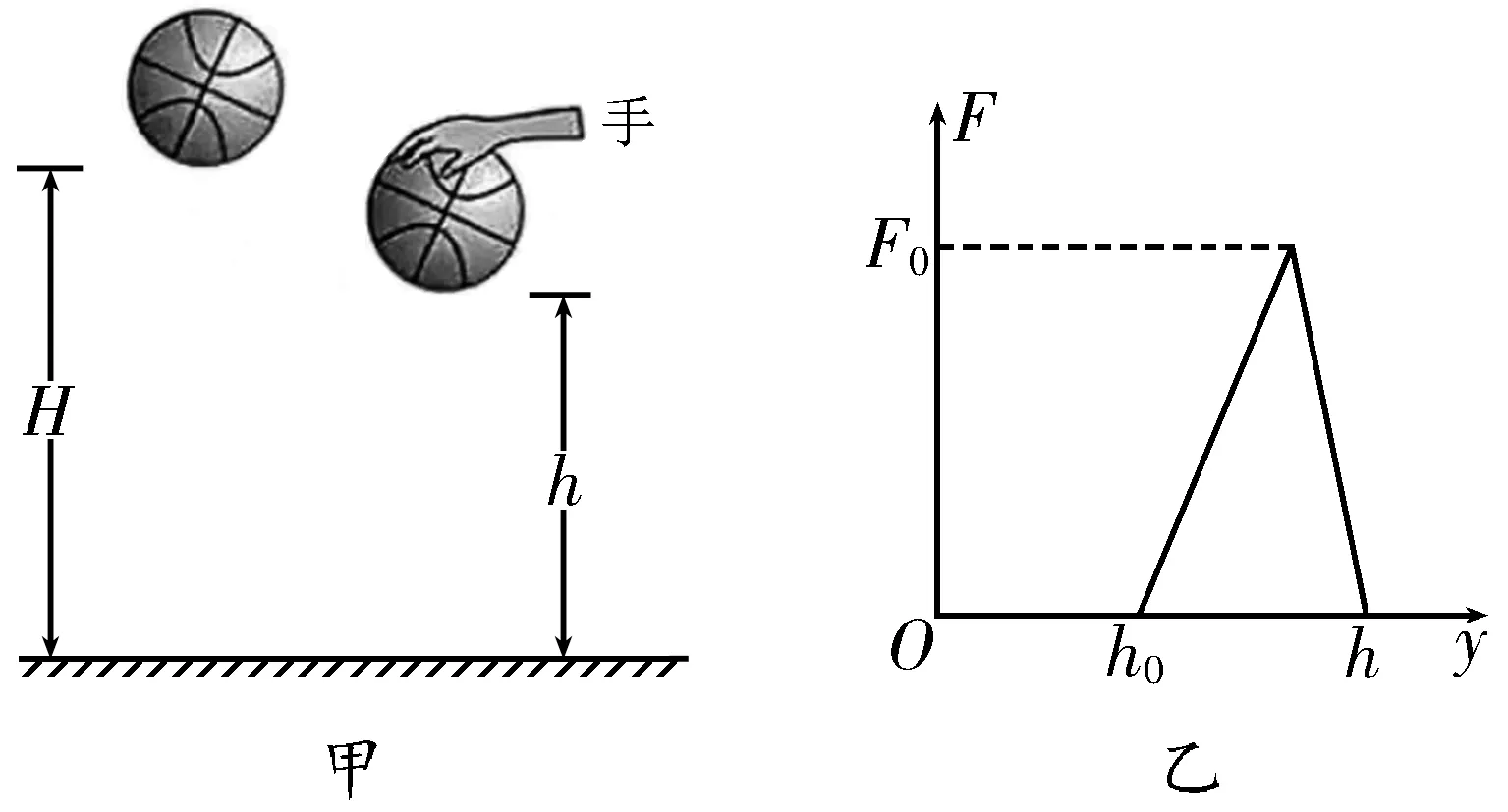
图1
(3)篮球从离地H高度处由静止下落后,每次反弹至最高点时,运动员拍击一次篮球(拍击时间极短),瞬间给其一个竖直向下、大小相等的冲量I,经过N次拍击后篮球恰好反弹至离地H高度处,求冲量I的大小。
解析:(1)篮球从离地H高度处由静止下落至地面的过程中,设篮球与地面碰撞的碰前速率为v前,根据动能定理得(mg-,解得篮球从与地面发生一次非弹性碰撞后到反弹至离地h的最高处的过程中,设篮球与地面碰撞的碰后速率为v后,根据动能定理得解得v后=因此篮球与地面碰撞的碰后速率与碰前速率之比
说明:由题意知篮球与地面发生的碰撞为非弹性碰撞,则解得,这与题目中给出的常数λ的范围一致。
(2)篮球反弹至离地h的最高处时,运动员对篮球施加一个向下的压力F,力F随高度y的变化图像与横轴围成的图形的面积表示变力F所做的功。篮球从离地h高度处下落至地面的过程中,设篮球与地面碰撞的碰前速率为v1,根据动能定理得(mg-λmg)h+篮球再次反弹至离地h高度处的过程中,设篮球与地面碰撞的碰后速率为v2,根据动能定理得- (mg+因为篮球每次与地面碰撞的碰后速率与碰前速率之比相同,即所以(mg-λmg)h+,解得F0=
(3)篮球从离地H高度处由静止下落后,每次反弹至最高点时,运动员拍击一次篮球,瞬间给其一个竖直向下、大小相等的冲量I,由于拍击时间极短,重力的冲量可以忽略不计,设击球瞬间篮球获得的速度为v0,选竖直向下为正方向,根据动量定理得I=mv0,即每次击球瞬间篮球获得的速度为定值。如图2所示,设篮球从离地H高度处由静止下落后,第一次反弹至最高点运动员拍击篮球后,下落过程中的下落高度记为h0=h,着地速率为v1,反弹速率为v1',反弹后上升的最大高度为h1;第二次反弹至最高点运动员拍击篮球后,下落过程中的下落高度为h1,着地速率为v2,反弹速率为v2',反弹后上升的最大高度为h2;…;第n次反弹至最高点运动员拍击篮球后,下落过程中的下落高度为hn-1,着地速率为vn,反弹速率为vn',反弹后上升的最大高度为hn。
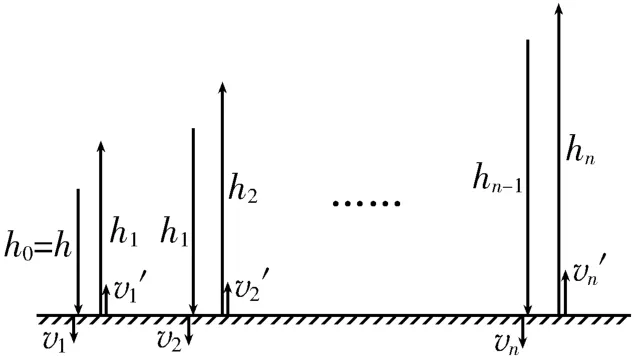
图2
第n次反弹至最高点运动员拍击篮球后,在篮球下落的过程中,根据动能定理得在篮球反弹后上升的过程中,根据动能定理得-(mg+篮球与地面碰撞的碰后速率与碰前速率之比解得hn=代入得令,则hn=phn-1+q(n≥1,h0=h),即数列{hn}为一阶线性递推数列。求数列{hn}的通项公式可以采用以下两种方法。
方法一:构造等比数列法。引入待定常数α,使hn-α=p(hn-1-α),则hn=phn-1+(1-p)α,对比递推公式hn=phn-1+q,再令(1 -p)α=q,解得故数列{hn-α}是以h0-α=h-α为首项,p为公比的等比数列。因此hn-α=pn(h0-α)=pn(h-α),即hn=pn(h-α)+α。
方法二:累加相消法。将递推公式hn=phn-1+q(n≥1,h0=h)两边同时除以pn得,则,将以上n式相加得,根据等比数列求和公式得,则令即,将上式两边同时乘以pn得hn=pn(h-α)+α。
已知经过N次拍击后篮球恰好反弹至离地H高度处,即hn=H,代入数列{hn}的通项公式得(h-α)+α,解得α=又有因此
说明:(3)问要求经过N次拍击后篮球恰好反弹至离地H高度处,即要求运动员每次拍击篮球后反弹上升的最大高度越来越大,此过程具体是如何实现的呢? 根据数列{hn}的通项公式hn=pn(h-α)+α,其中p=<1 可知,pn是递减的,要使hn递增,则需pn的系数h-α<0,即要求h<,解得另外,令n→∞,则pn→0,hn→α=,即当时,运动员每次拍击篮球后篮球反弹上升的最大高度hn递增,但hn有极限,不会无限增大。
二、对高考原题的评析
本题(1)问考查动能定理的应用(也可以运用运动学公式和牛顿第二定律联立求解),(2)问在考查动能定理的基础上进一步考查计算变力做功的一种常用方法——面积法,即力F随高度y的变化图像与横轴围成的图形的面积表示变力F所做的功,(1)(2)两问都很基础,不偏不怪。(3)问的难度较大,考查了一种重要的数学方法——递推法,考查利用数学知识解决物理问题的能力。所谓递推法,即当问题中涉及的物理过程较多,且各物理过程具有相同的特点和遵循相同的规律时,可选取有代表性的任一物理过程分析,得出联系相邻物理过程的相关物理量的递推关系式,再根据递推关系式求解相关物理量的通项公式,从而达到解决问题目的的一种科学思维方法。构造等比数列法和累加相消法是求递推数列通项公式的常用方法,由数列的递推公式求通项公式需要抓住递推数列的递推关系,分析结构特征,进行合理变形。
三、探究篮球自由弹跳过程中运动的总路程
变式探究1:将本题(3)问改为篮球从离地H高度处由静止下落后,每次反弹至最高点时,让篮球在空中自由弹跳直到最终静止于地面上,求篮球自由弹跳过程中运动的总路程。
解析:根据上述得出的递推公式hn=可知,若篮球每次反弹至最高点时,运动员并不拍击篮球,即令v0=0,则hn=(n≥1,h0=h),显然数列{hn}是以h0=h为首项,p=<1为公比的等比数列。因此hn=pnh0=故篮球在空中自由弹跳过程中运动的总路程s=H+2(h0+h1+h2+…+hn-1+…),根据等比数列求和公式得
变式探究2:将本题改为质量为m的篮球从离地H高度处由静止下落,与地面发生一次弹性碰撞后反弹至离地h的最高处。设篮球在运动过程中所受空气阻力的大小恒定,且篮球每次与地面的碰撞为弹性碰撞,求篮球在空中自由弹跳过程中运动的总路程。
解析:篮球从离地H高度处由静止下落,与地面发生一次弹性碰撞后反弹至离地h的最高处,设篮球在运动过程中所受空气阻力大小为f,对此全过程应用动能定理得mg(H-h)-f(H+h)=0,解得f=设篮球在空中自由弹跳过程中运动的总路程为s,对自由弹跳的全过程应用动能定理得mgH-fs=0,解得
说明:变式探究2 与变式探究1 得出的结果完全相同。事实上用递推法同样可以证明变式探究2情形下篮球每次反弹后上升的最大高度仍然是以h0=h为首项,p=为公比的等比数列,因此篮球在这两种自由弹跳过程中运动的总路程相同。
证明:篮球第n次反弹至最高点后,在篮球下落的过程中,根据动能定理得(mgf)hn-1=在篮球反弹后上升的过程中,根据动能定理得-(mg+f)hn=0-若篮球每次与地面的碰撞为弹性碰撞,则vn'=vn,联立以上各式解得hn=,将代入得hn=
