基于敏感器探测率的红外探测识别判据

唐万杰，李 明，张静静，刘小锋

(1 吉林江机特种工业有限公司，吉林 吉林 132000；2 淮海工业集团有限公司，山西 长治 046000)

0 引言

末敏弹是一种用于攻击自行火炮、坦克、步兵战车等装甲目标的新型弹药。在弹道末段抛出末敏子弹，目标敏感装置在末敏子弹的帯动下，以一定的转速、下降速度和扫描角对地面背景及目标进行密集的扫描探测，一旦遇到目标并且满足识别条件，即输出识别信息，起爆子弹战斗部击毁目标。

目前，国内外的末敏弹有多种探测目标的复合模式，其中红外探测是必不可少的模式，通常由红外敏感器来实现对目标红外辐射特征的探测。因此，研究敏感器的红外探测特性显得尤为重要。

多年来，诸多学者对末敏弹的仿真和探测进行了大量的研究，不乏有敏感器的探测识别与稳态扫描平台模型[1]；通过虚拟视场样机模拟生成红外敏感器扫描虚拟场景所产生的红外数字信号，实现对末敏弹的半实物图像实时仿真[2]；结合末敏弹的扫描姿态等物理模型，通过正交试验的灵敏度分析法，对影响末敏弹系统效能的多个因素进行分析，以获得末敏弹系统最佳搭配参数[3]。这些研究大多是半实物图像仿真，缺少对红外探测系统识别判据的研究，针对此问題，文中提出了基于末敏弹红外敏感器探测率的红外探测识别判据。

1 研究基础

1.1 扫描平台模型

设红外敏感器(以下简称敏感器)的扫描角为θ，转速为n，下落速度为v，子弹起始稳态扫描高度为H。如图1所示，在理想条件下，敏感器在地面上的扫描轨迹为阿基米德螺旋线，再考虑风速的影响，设风速在x轴、y轴方向上的分量分别为vx，vy，在稳态扫描起始高度时敏感器对应的地面坐标为(x0，y0)，则扫描线上任意点的坐标方程[1]为：

图1 扫描平台模型

x=x0+vxt+(H-vt)tanθcos(α0+2πnt)

(1)

y=y0+vyt+(H-vt)tanθsin(α0+2πnt)

(2)

1.2 目标辐射功率

图2为扫描线扫入目标的示意图，图中圆圈为探测视场的投影面积，(x0,y0)为扫描线坐标，(xc，yc)为目标中心坐标，a，b分别为目标热区的长和宽，A为扫描线扫入目标的点，A′为扫描线离开目标的点。此时，目标热区的面积可表示为：

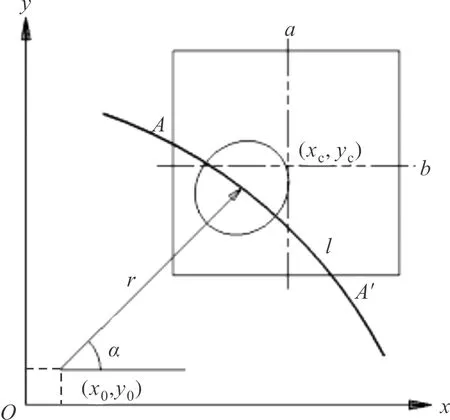
图2 扫描线扫入目标的示意图

(3)

依据红外辐射理论，大多数绝缘材料表面，在相对表面法线方向的观察角不超过60°时，都遵守朗伯余弦定律[4]。凡遵守朗伯余弦定律的辐射表面为朗伯辐射源，其辐射亮度是一个与方向无关的常量。太阳、荧光屏、坦克表面等都近似于这种光源[5]。在均匀背景下，到达敏感器探测视场内的目标辐射功率[5]为：

(4)

式中：τ为敏感器光学系统透射率；A0为光学系统的入瞳面积；R为目标与光学系统的距离；As为目标的辐射面积；ΔL为目标相对于背景在敏感波段内的辐射亮度[6]，ΔL=f(Ta,Tb),其中Ta，Tb分别为目标及背景的辐射温度。

ΔE=ΔL×τ×A0×π×tan2δ

(5)

式(5)表明目标辐射功率仅与敏感器的光学系统透射率、入瞳面积、视场角以及目标辐射亮度有关，与探测距离和辐射面积无关。

2 红外探测识别判据

对于敏感器使用的红外探测器而言，其探测率的计算式[7]为：

(6)

式中：Vs为响应信号；Vn为噪声；P为入射到探测器的辐射功率。

由于敏感器与红外探测器均具有接收红外辐射能量、输出电信号的特点，比照式(6)，推出敏感器的探测率为：

(7)

式中：Us为敏感器的响应信号；Un为含有背景杂波的噪声；E为入射到敏感器的目标辐射功率。这里的探测率B表示单位辐射功率辐照在敏感器上所获得的信噪比。对于一个给定的敏感器，由于其红外探测器和电路等参数已经确定，其响应特性也已固定，因此它的B值是一个比例常数。则信噪比Rsn为：

(8)

式(8)为基于敏感器探测率的红外探测识别仿真数学模型，表明了红外探测信号的信噪比与探测率和目标辐射功率成正比。

根据式(8)，以敏感器探测率与探测视场内的目标辐射功率的乘积(即信噪比Rsn)大于某一数值，作为识别目标的判据之一，即可实现对目标的识别功能。在实际使用中，为保证末敏子弹对目标有一定的命中率，要求敏感器视场深入目标热区一定范围，使其信噪比满足判别准则。取m为识别准则[8]中要求的最小值，当Rsn≥m时，确认识别目标。

3 仿真与分析

3.1 算法和参数设置

利用Matlab的矩阵数据处理能力，在设置初始参数的条件下以时间为变量，依据上述原理建立数学模型，并进行编程仿真计算。取t=H/v，将t以0.5 ms的间隔细分，计算各个时刻的坐标及其高度值，实现基础数值计算。再利用函数“find”的查找元素“下标”功能，获得符合目标区域的扫描区域(x，y)及其相应的高度值，进而计算出目标辐射功率。在给定敏感器探测率的基础上，即可获得红外探测信号的信噪比，从而确认是否识别目标。

在计算目标辐射功率时，针对进入探测视场的目标辐射面积随扫入方向随机变化的情况，为了减少误识别，简化计算，将图2中目标辐射面积As的计算方法分为两种情况：

1)若AA′弦长l大于等于2倍的探测视场直径，在绝大部分情况下目标充满探测视场，进入探测视场的辐射源为完整椭圆形，目标辐射面积按照椭圆形面积计算，即短轴为探测视场直径d，长轴为d/cosθ，目标辐射功率按式(5)计算。

2)若AA′弦长l小于2倍的探测视场直径，在绝大部分情况下目标未充满探测视场，进入探测视场的辐射源是不完整椭圆形。目标的有效辐射面积均按照以弦l为短轴、l/cosθ为长轴的椭圆形面积的二分之一计算，目标辐射功率按式(4)计算。

仿真计算界面如图3所示。

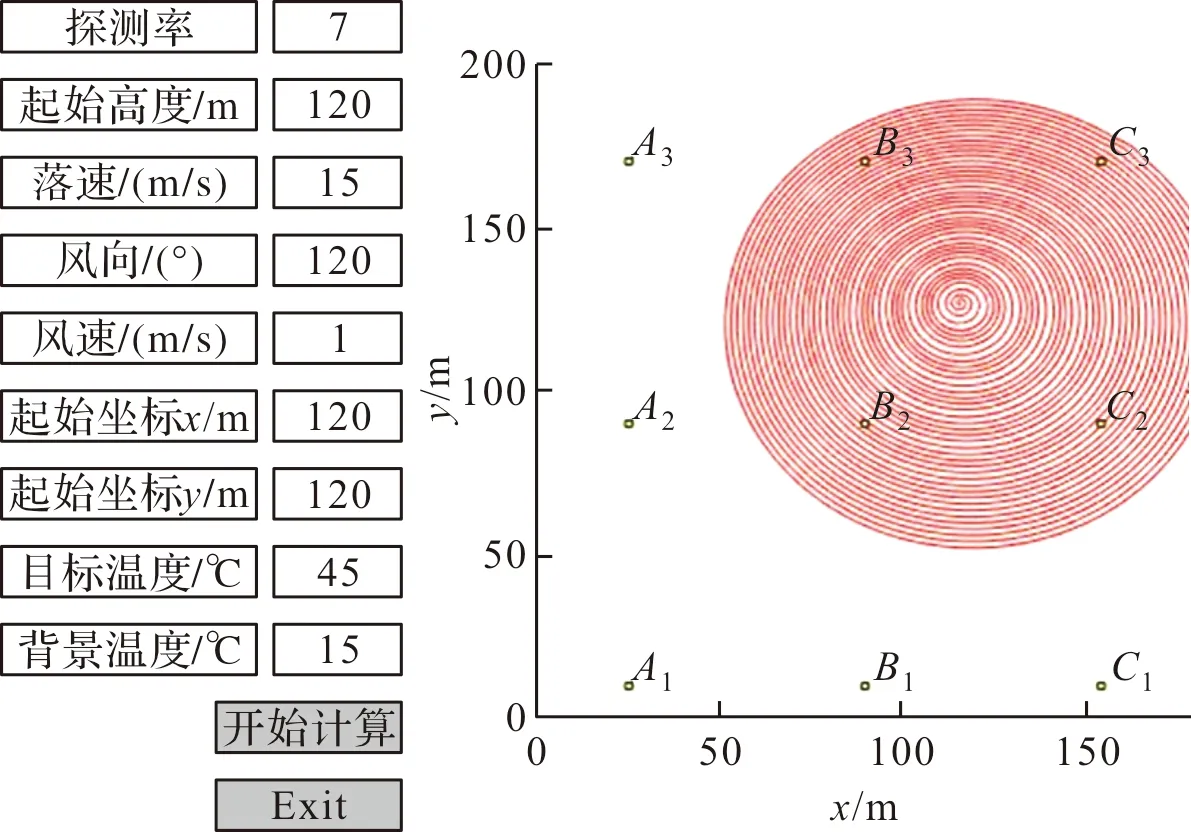
图3 红外敏感器扫描探测仿真计算界面

为了简化计算，假设目标和背景的辐射温度是均匀的，并且目标相对于扫描视场是静止的。目标设置为3×3的阵列，列间距为65 m，行间距为80 m。每个目标热区长宽均为2 m，如图3中的黑色方块所示。计算参数为：扫描起始高度120 m，落速15 m/s，风向北偏西30°，风速1 m/s，背景温度15 ℃，扫描角30°，探测视场0.8°，转速5 r/s[1,3]。

3.2 仿真结果与分析

在计算中，为了验证探测率B对敏感器探测识别的影响，分别取B为7、4.7、3.5，信噪比m为4.5进行仿真。由于目标的动力舱上表面的辐射强度较大，主要集中在7～14 μm波段[9]，温度分布在十几摄氏度至几十摄氏度之间[10]，因此，在计算式(6)的辐射亮度时波段取7～14 μm，目标与背景的温度差[11-12]取15～30 ℃。扫描起始高度对应的地面坐标位置范围是横向0～180 m，纵向0～180 m，纵横间距均为20 m，共计100个仿真计算点位。

通过仿真计算得到在不同探测率、不同温差条件下，100个仿真计算点位总的识别目标次数以及不能识别目标的点位数，见表1。

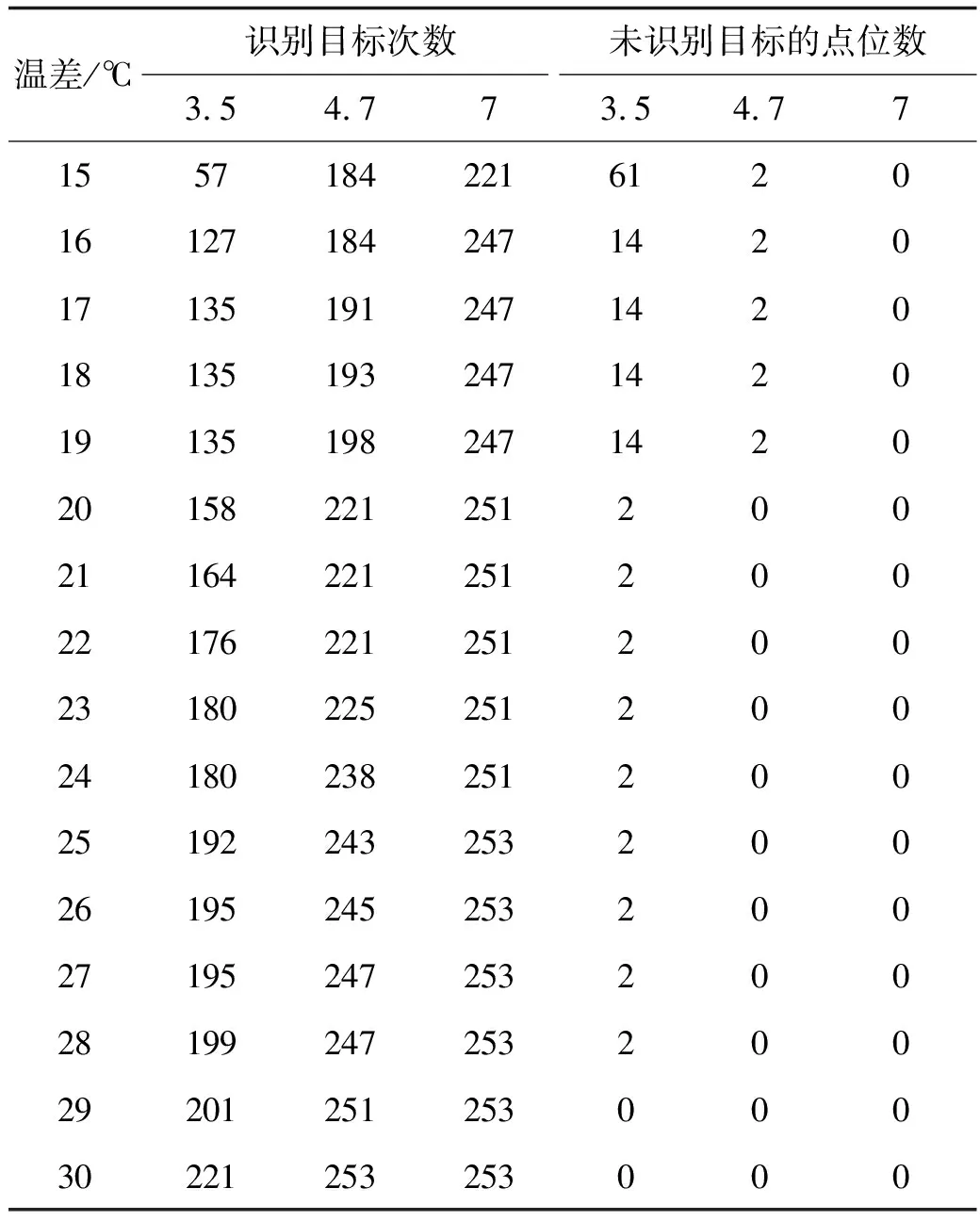
表1 不同探测率不同温差时的识别目标情况

图4～图6展示了3个信噪比、3个温差条件下识别目标的次数。图中的小圆圈为扫描起始高度对应的地面坐标位置，也即仿真计算点位。小圆圈右边的3个数字依次表示在16 ℃、20 ℃和29 ℃温差时的仿真计算识别目标的次数。

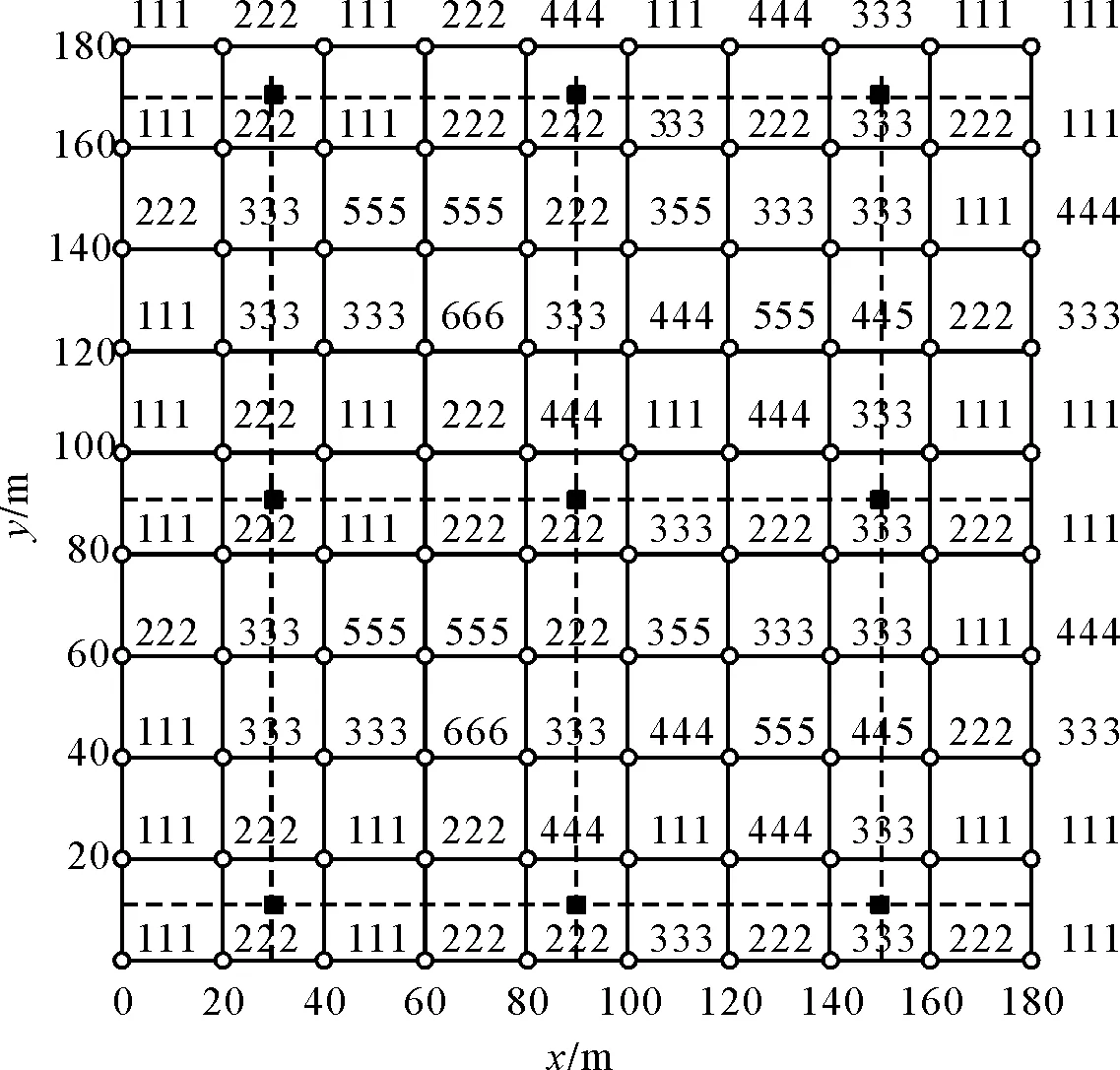
图4 Rsn=7、不同温差时的识别目标次数

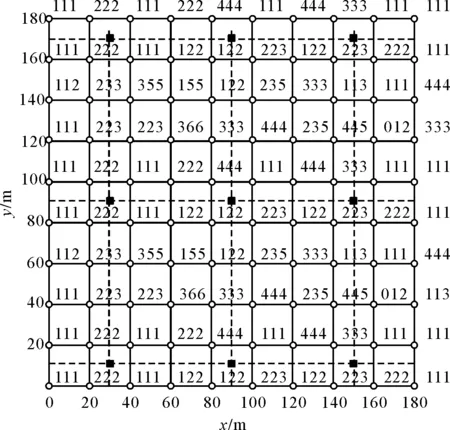
图5 Rsn=4.7、不同温差时的识别目标次数

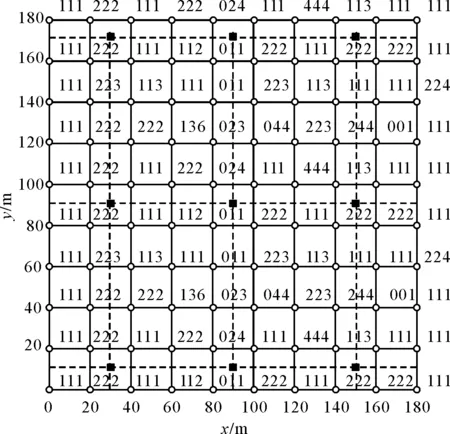
图6 Rsn=3.5、不同温差时的识别目标次数

由图4～图6可以看出：

1)当Rsn=7时，100个仿真计算点位在3个温差下均可探测识别目标。

2)当Rsn=4.7时，随着温差的升高，由于目标辐射功率的增加，使得信噪比提高，识别目标的次数逐渐增加。当温差不低于16 ℃时，98%的仿真计算点位可以识别目标。

3)当Rsn=3.5时，在温差不低于20 ℃时，98%的仿真计算点位可以识别目标。

4)在同一温差条件下，随着探测率的升高，信噪比提高，识别的次数逐渐增加。

上述结果符合信噪比与探测率和辐射功率成正比的规律。

为了使不同探测率的敏感器均能识别出98%以上的目标，目标与背景的温差应不低于20 ℃。这与实际验证结果一致。

4 结论

文中提出了基于红外敏感器探测率的末敏弹单元红外探测识别判据，将敏感器的探测率与探测视场内的目标福射功率的乘积等价为探测信号的信噪比，并依此作为识别目标的判断依据。利用敏感器的扫描平台数学模型和目标热区与背景的温度差值，计算目标福射面积和辐射功率，进行识别仿真计算。结果表明，在敏感器的探测率达到一定数值、且目标与背景存在正20 ℃以上的温差条件下，即可实现对集群目标的探测和识别；在温差不变时，随着探测率的提高，敏感器输出信号的信噪比增加，识别率提高；这些仿真结果都与实测结果相吻合，表明基于红外敏感器探测率的末敏弹单元红外探测识别判据，可以真实反映敏感器对目标的探测能力，对今后末敏弹红外探测研究具有一定的指导意义。