基于BP神经网络的星箭界面动载荷识别
2023-03-20陈树海郭安丰吴邵庆费庆国
陈树海, 郭安丰, 吴邵庆, 费庆国
(1. 东南大学 机械工程学院, 南京 211189; 2. 东南大学 土木工程学院, 南京 211189;3. 上海卫星工程研究所, 上海 201109)
星箭界面动态载荷指火箭发射过程中受到横向载荷的作用,在星箭连接界面上产生的弯矩和剪力,其载荷信息是地面验证试验和可靠性评价的重要依据[1]。虽然在星箭连接界面布置力传感器能够直接获取界面动载荷,但它会改变星箭结构的动力学特性,真实星箭结构一般不允许搭载力测量装置[2];基于星箭耦合动力学模型开展耦合载荷分析,也能够获取界面处的动载荷,但是该方法需要准确的星箭耦合有限元分析模型、可靠的力学环境预示方法以及准确的火箭外载荷输入[3]。在卫星结构设计时,依靠卫星结构自身的振动响应反演卫星结构受到的基础加速度激励,并进一步估计星箭界面动载荷,能够避免复杂火箭结构的建模和星箭耦合振动分析,有利于实现服役工况下星箭界面动载荷的在线预测。
基于卫星结构响应反演星箭界面动载荷已有一定的研究成果。朱斯岩等[4]利用星箭结构的Craig减缩模型,先由已知的界面自由度加速度时间历程求解基础激励,并重构结构全场加速度响应,最后代入结构动力学方程求解星箭界面动载荷;Craig减缩模型能够降低载荷识别计算量,但模型误差也将导致载荷识别结果的更大误差。张永涛等[5]基于星箭连接环的理论模型和测量应变与界面力的对应关系,提出一种通过实测星箭连接环应变反演星箭界面力的方法;该方法中采用了薄壁圆筒模型近似星箭连接环,连接环的模拟误差降低了识别结果的精度。尹健等[6]基于B样条拟合星箭界面动载荷的分布函数,建立了卫星结构加速度与界面分布动载荷的传递关系,提出了一种星箭界面环形分布动载荷的识别方法,然而该方法中未能考虑模型误差的影响;Wu等[7]考虑了星箭界面力学参数的不确定性,提出一种随机动力学系统上的随机动载荷识别方法,利用卫星结构振动响应样本识别了卫星结构底部随机振动激励。
利用结构有限元模型开展动载荷反演[8-9],有限元模型误差和动载荷识别算法误差将会叠加,目前只能是利用模型修正技术尽量提高有限元模型的模拟精度[10],以获得更加准确的载荷-响应传递关系。当星箭结构模型存在局部非线性时,载荷-响应传递关系更加复杂,有限元模型模拟精度将进一步下降,造成载荷识别结果的较大误差。近年来,智能识别算法在载荷识别领域越来越得到重视[11-13],有望降低模型和识别算法双重误差对载荷识别结果的影响。
实际服役过程中,星箭界面采用对接环连接,无法通过直接安装传感器测量界面动载荷,但是卫星结构加速度以及星箭界面处的加速度均可以测量。基于BP神经网络方法的动载荷识别技术一般直接将动载荷-结构响应样本作为神经网络训练的输入-输出,在星箭界面动载荷识别问题中难以实现。本文针对星箭界面动载荷识别提出了一个新的思路,即先使用实测星箭界面加速度激励和卫星结构加速度响应构建的样本库来构建两者之间传递关系的神经网络代理模型,进而利用实测卫星结构加速度响应识别星箭界面加速度激励,最后将识别得到的星箭界面加速度激励施加于高保真的卫星结构有限元模型,分析得到星箭界面动载荷。所提出的新方法能够利用实测数据训练得到更可靠的逆向代理模型,实现星箭界面动载荷的估计。本文研究有望实现服役状态下星箭界面动载荷的在线预测。
1 基于BP神经网络的星箭界面动载荷识别
1.1 卫星结构激励与载荷的传递关系
卫星结构加速度与星箭界面力存在如下关系

(1)

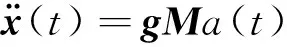
(2)
令G=gM,则G={Gij}表示联系基础加速度激励与结构加速度响应的传递关系矩阵,其元素Gij表示在第j个位置作用单位脉冲加速度激励时在第i个位置的卫星结构加速度响应。利用式(1)或(2)的直接求逆可以识别界面力或基础加速度激励,但识别结果会受到结构模型和病态矩阵求逆双重误差叠加的影响,当结构模型不准确时,甚至会导致完全无法识别外载荷。
1.2 基于BP神经网络的载荷识别
动载荷反演的本质是构建响应与载荷的逆向传递关系,利用BP神经网络能够学习和表征输入-输出之间的非线性映射关系,且无需预知描述这种映射关系的数学方程。它采用梯度下降法的学习规则,通过反向传播修正来不断调整权值和阈值,最终使网络的误差平方和最小。因此,利用BP神经网络模拟G矩阵中的映射关系,将基于BP神经网络的动载荷识别方法应用于卫星基础加速度激励和星箭界面力识别,能够有效避免由于卫星结构模型和病态矩阵求逆双重误差叠加,提高识别的精度。
本文构建用于识别卫星结构基础加速度激励的BP神经网络结构如图1所示。
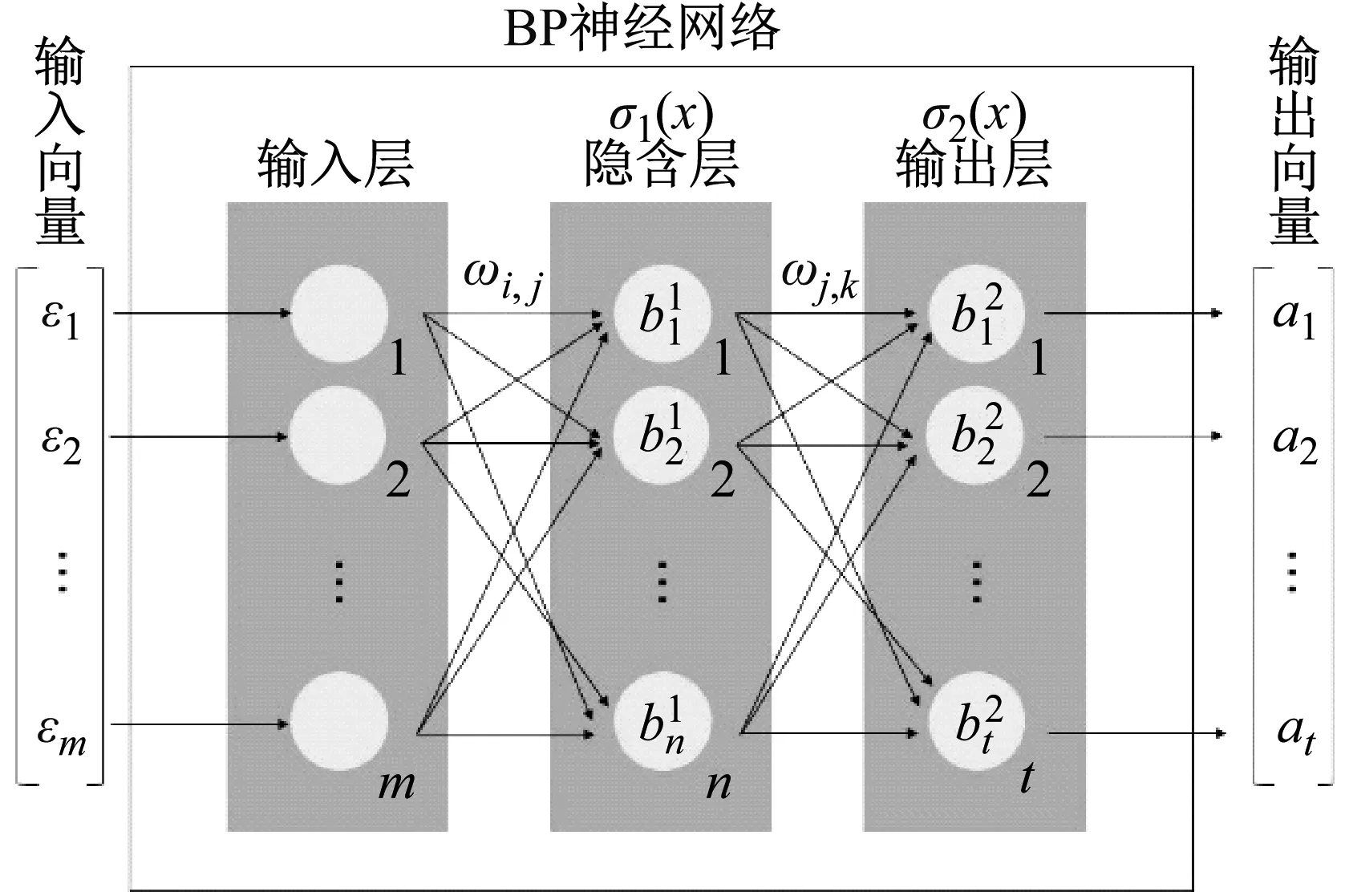
图1 BP神经网络结构图Fig.1 Structural diagram of BP neural network
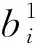

(3)
其次,根据隐含层激活函数σ1(x)计算隐层单元的输出。隐含层第i个节点的输出yi根据下式计算
(4)

(5)
最后,根据输出层激活函数σ2(x)进而得到输出层单元的输出。输出层第k个节点的输出ak计算如下
(6)
根据上述过程可以得到神经网络的输出,再根据输出的结果进行BP神经网络的误差反向传播。此过程将实际输出与训练指定输出之间的误差反向传播给网络上层,来调节各阶层权值,最终完成网络训练。从输出层开始,求取各个神经元的输出误差,进而采用误差梯度下降法调节各层网络的权值和阈值,使得最终调节后的网络输出能够很好地接近预定输出值。

(7)
各层权值δwk及误差δbk分别为
(8)
(9)
式中,参数η为调节因子,代表学习速率。
依据上述方法可完成对BP神经网络各层权值和误差的调整,每次调整都可以使总误差函数值下降。通过将调整后网络的总误差值与预设的精度进行比较,最终达到精度或者达到最大训练次数则停止训练,否则循环迭代不断调整网络参数,此调整过程称为神经网络学习过程,通过学习过程最终得到满意的权值、误差和网络结构。BP神经网络构建流程如图2所示。

图2 BP神经网络构建流程图Fig.2 Flow chart of BP neural network construction
基于BP神经网络的星箭界面动载荷反演步骤如下:
(1) 建立训练样本并进行归一化处理。仿真算例中,基于卫星结构有限元模型开展仿真分析获取样本;试验验证中,直接采用实测响应作为输入-输出样本。基于卫星结构,取基础加速度激励与结构加速度响应信号形成训练样本集合,其中70%数据作为训练集,15%数据作为验证集,15%数据作为测试集。训练集主要是对数据样本进行模拟拟合,验证集负责寻找最优的网络深度,测试集负责测试最终模型的泛化能力,即预测的准确性。
(2) 明确最大训练次数、学习精度、学习速率以及各层节点数等参数。本文所建立的BP神经网络,最大训练次数为10 000次,学习精度为1×10-7,学习速率为0.01,输入层节点数为n,分别为当前时刻以及前n个时刻的响应信号。输出层节点数为1,即当前时刻的基础加速度激励。相应的隐含层单元节点数依据经验公式取为log2n[14]。
(3) 开展动载荷识别。结合实测卫星结构加速度响应数据和训练得到的BP神经网络,识别得到卫星结构上的基础加速度激励,并将基础加速度激励作用于高保真卫星结构动力学模型,获取星箭界面动载荷。
2 仿真算例
2.1 卫星结构有限元模型
如图1(a)所示卫星结构由法兰盘、主承力筒、侧板、隔板、L型压条及M3螺钉连接件组成。构件材料和尺寸如表1所示。卫星结构上各部件采用六面体实体单元建模。采用等效线性化的薄层单元来模拟各部件之间的螺栓连接和接触。卫星结构有限元模型如图3(b)所示。

表1 卫星结构主要构件尺寸Tab.1 Dimensions of the main components in the satellite structure
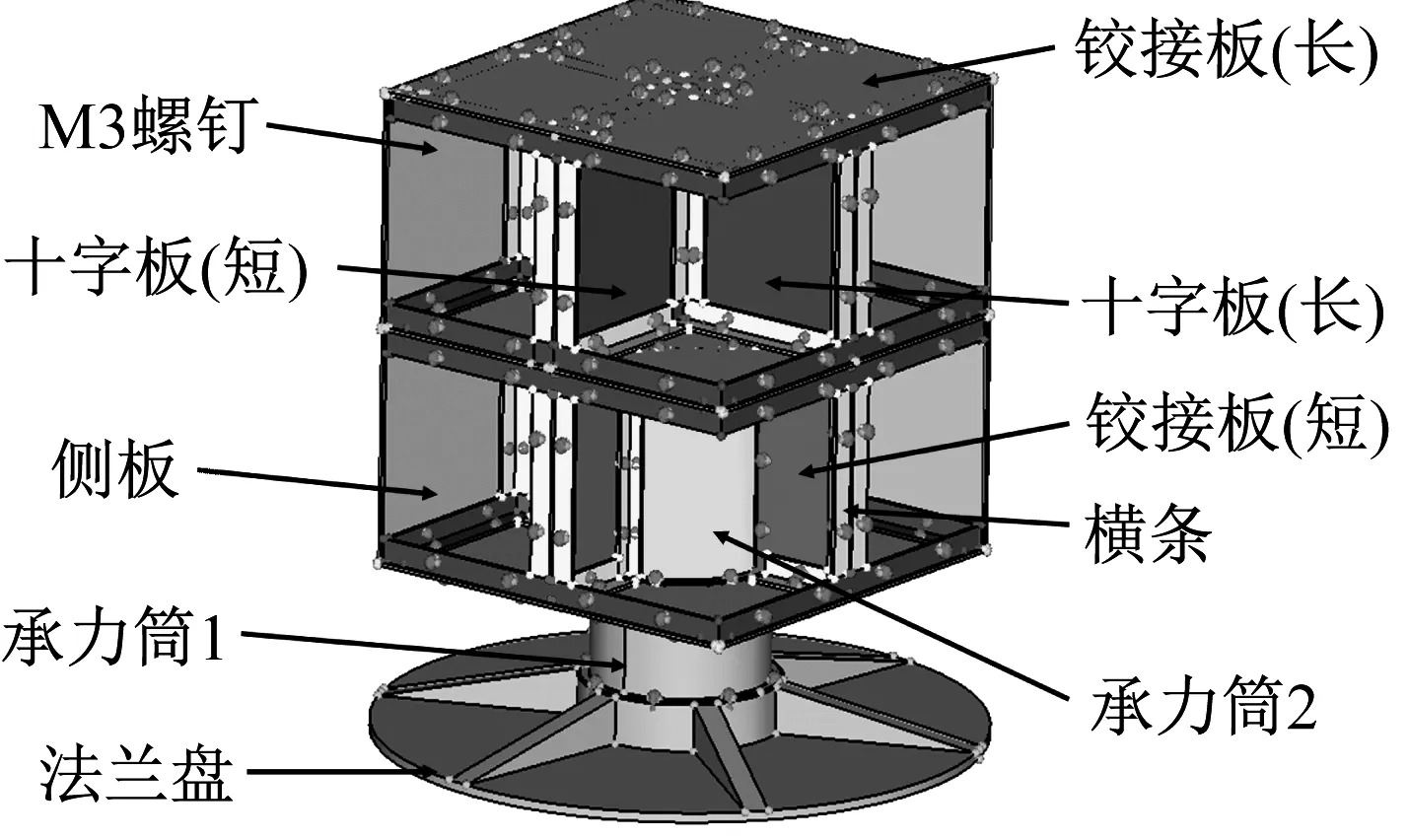
(a) 几何模型

(b) 有限元模型图3 卫星结构及有限元模型Fig.3 Satellite structure and finite element model
实际服役状态下的星箭界面动态载荷是难以直接测量的。本研究设计了如图4(a)所示的力测量工装,用于实验室条件下测量振动试验中振动台与卫星结构之间传递载荷,以验证本文方法识别得到的星箭界面动载荷的有效性。力测量工装中包含卫星结构与振动台的连接装置以及用于测量传递载荷的力传感器;利用六个力传感器连接上方法兰盘和下方底座,底座通过M16螺栓与振动台台面连接。力测量工装各部件的材料和尺寸如表2中所示。建立如图4(b)所示力测量工装有限元模型,其中结构件和力传感器采用实体单元模拟,各螺栓连接和接触部位采用薄层单元模拟。图5中给出了带力测量工装的卫星结构有限元模型。

图4 力测量工装及其有限元模型Fig.4 Force measuring tooling and its finite element model

图5 带力测量工装的卫星结构有限元模型Fig.5 Finite element model of the satellite structure with force measuring tooling

表2 力测量工装材料及尺寸Tab.2 Material and dimensions of the force measuring tooling
2.2 正弦激励工况
选取正弦基础加速度激励的频率为70 Hz,介于带力测量工装的卫星结构模型的第1阶和第2阶固有频率之间,振动幅值为0.5 m/s2,采样频率设定为512 Hz。基础加速度激励通过大质量法施加在力测量工装结构有限元模型底部,如图5所示。
通过有限元分析得到测点处结构的仿真加速度响应。测点位置与试验模型测点1的位置相同,测点响应样本总数设定为3 072,其中70%数据作为训练集训练网络,15%数据作为验证集,15%数据作为测试集。利用训练获得的BP神经网络,以t,t+1,…,t+19时刻的加速度响应为输入,即可识别t时刻的基础加速度激励。基础加速度激励识别值与参考值的对比如图6所示。由图可知,本文的方法能够由卫星结构加速度响应精确识别卫星底部基础加速度激励,激励识别值和参考值之间的均方根误差趋向于0,其中均方根误差(root mean square error,RMSE)的计算由下式定义
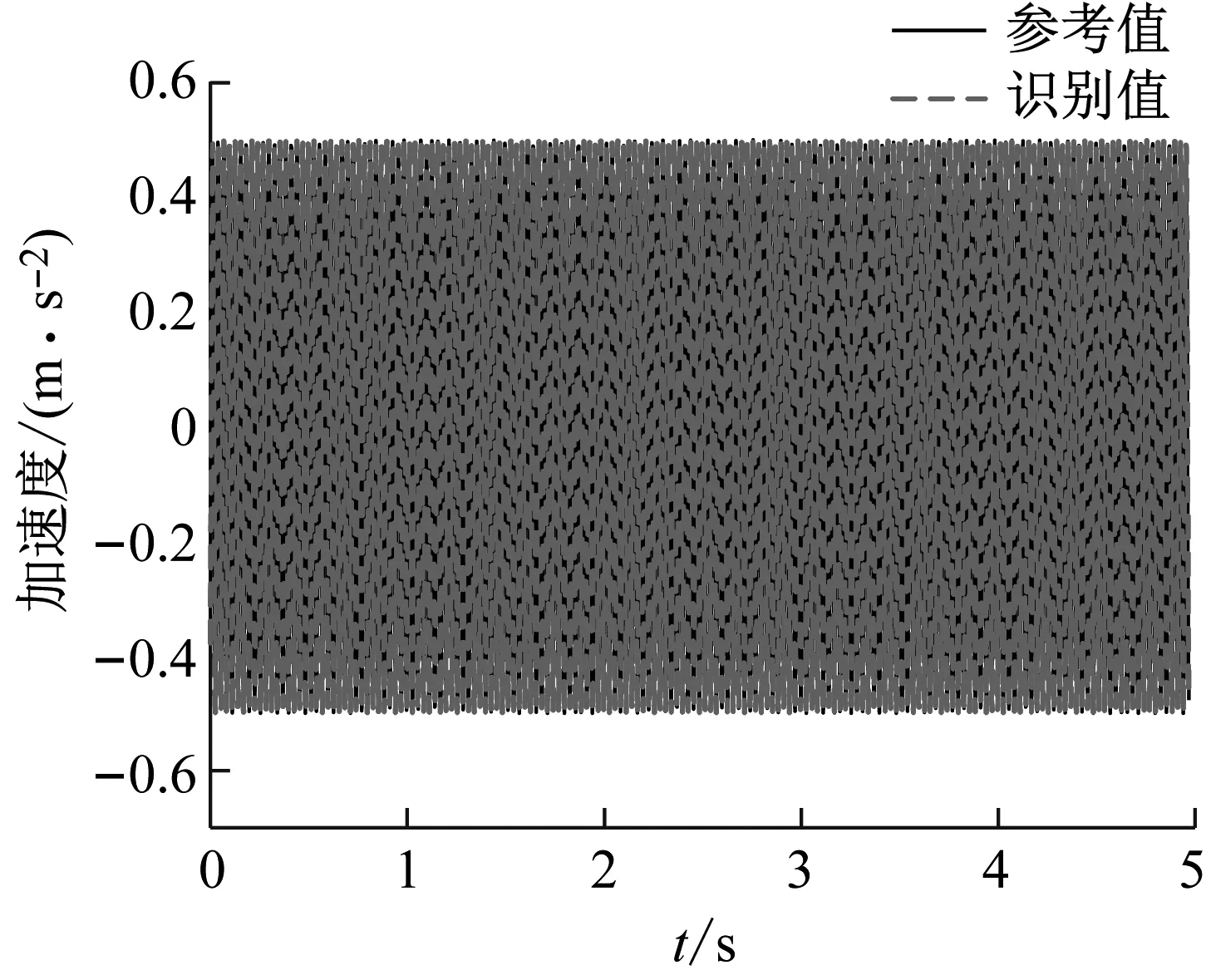
(a) 整体对比
(10)

为了研究该识别算法的抗噪声干扰能力,将仿真计算得到的卫星结构加速度响应信号分别添加2%、10%、20%的噪声,使用激励-带噪声响应样本集训练得到的神经网络开展基础加速度激励识别。信号添加噪声如下式所示
Yerr=Ycal+lnoise·std(Ycal)·rand(-1,1)
(11)
式中,Ycal和Yerr分别表示加噪声前后的响应样本;lnoise表示噪声水平;std(·)表示标准差;rand(·)表示随机扰动。
图7中给出了添加20%噪声工况下本文方法的识别结果。表3中给出了不同噪声水平下基础加速度激励的识别误差。结果表明,本文方法在加速度响应受不同程度噪声干扰的情况下均能够准确识别基础加速度激励,识别误差随着噪声干扰的增大略有增加,方法具有更好的抗噪声能力。

(a) 整体对比

(b) 局部放大图7 正弦基础加速度激励识别结果(20%噪声)Fig.7 Identification results of sinusoidal basic acceleration excitation (20% noise)

表3 不同噪声水平工况正弦基础加速度激励识别误差Tab.3 Identification errorsin sinusoidal basic acceleration excitation under different noise level
2.3 随机振动工况
实际卫星结构常承受随机振动激励,利用正弦激励-结构响应样本库训练得到的神经网络模型难以用于随机振动激励识别。因此本节开展基于随机激励-结构响应样本库的神经网络模型训练和基于卫星结构加速度响应的随机基础加速度激励识别。
参考随机基础加速度激励的功率谱密度函数如图8所示,激励频段为1~100 Hz。利用谐波叠加法得到随机基础加速度激励的样本,与2.2节中类似,开展带力测量工装卫星结构的振动分析,建立随机激励-结构响应样本库。

图8 随机基础加速度激励功率谱密度图Fig.8 Power spectral density of the random base acceleration excitation
图9中给出了利用仿真卫星结构加速度响应和训练后得到的神经网络模型识别的卫星底部随机基础加速度激励与参考值对比。结果表明了该识别模型对随机基础加速度激励识别的有效性。进一步,为验证基于随机激励-结构响应样本库训练的神经网络识别模型的普适性,将该识别模型用于2.2节中正弦激励的识别,识别结果如图10所示。结果表明该模型也能够较准确地识别正弦激励,识别结果的均方根误差8.489 5;反之,利用正弦激励-响应构建的神经网络识别模型则无法适用于随机基础加速度激励的识别。

(a) 整体对比
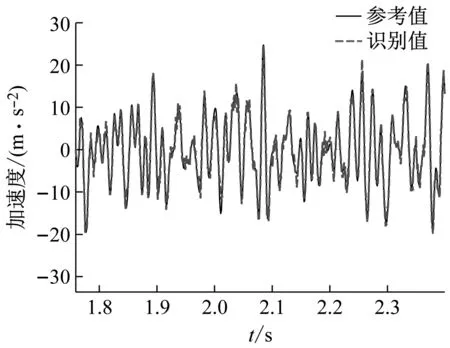
(b) 局部放大图9 随机基础加速度激励识别结果Fig.9 Identification results of random base acceleration excitation

图10 利用随机激励-响应神经网络模型识别正弦激励Fig.10 Identified sinusoidal excitation by using the random excitation-response neural network model
3 基础加速度激励和界面动载荷识别试验验证
3.1 振动试验系统
为验证本文提出的载荷识别方法。搭建如图11所示试验系统。卫星结构模型底端串联力测量工装,固定在振动台台面上。在卫星结构上施加横向基础加速度激励,开展结构振动试验,利用振动台面加速度数据和卫星结构顶部测点加速度响应训练载荷反演的神经网络模型,开展基于实测结构加速度信号的基础加速度激励识别并利用实测振动台面加速度验证;同时,将识别获得的基础加速度激励作用于结构有限元模型,计算振动台与卫星结构连接界面间的传递载荷,利用力传感器测量得到的振动台与卫星结构间传递载荷验证识别的界面动载荷。

图11 卫星结构基础加速度激励试验图Fig.11 Baseacceleration excitation test of the satellite structure
值得注意的是,实际星箭连接界面上的动载荷应该连续分布的。但由于分布动载荷的测量存在较大困难,本研究在试验验证中,采用了六个三向力传感器测量得到的集中载荷等效星箭界面上的连续分布动载荷,并利用动载荷识别值与实测值对比来验证识别方法的有效性。试验中共有6个加速度信号采集通道以及18个力信号采集通道。振动台在水平方向激振,载荷工况有两种:分别是频率为70 Hz,大小为0.5g的正弦激励以及频率范围为5~100 Hz,大小为0.2g的正弦扫频激励。
3.2 识别结果
利用图11中测点1采集得到的卫星结构加速度响应信号以及振动台面实测加速度激励构成的样本,训练用于载荷识别的神经网络;进一步利用实测卫星结构加速度反演基础加速度激励。正弦激励以及正弦扫频工况下振动台面的加速度激励识别结果分别如图12和13所示。结果表明:基于本文方法构建的神经网络识别模型能够准确的识别振动台面在正弦和扫频工况下的加速度激励,识别结果的均方根误差分别为0.001 7和0.005 9。利用实测卫星加速度响应和振动台面加速度激励信号训练神经网络识别模型,能够免去卫星结构有限元建模和模型修正环节,同时能够一定程度上避免结构有限元模型误差对基础加速度激励识别结果精度的影响。

图12 正弦激励下振动台面加速度激励识别结果Fig.12 Identification results of acceleration excitation on shaking table surface under sinusoidal excitation
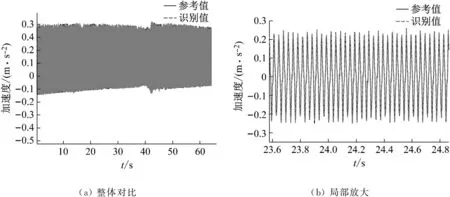
图13 正弦扫频激励下振动台面加速度激励识别结果Fig.13 Identification results of acceleration excitation on shaking table surface under swept-sin excitation
将基于神经网络方法识别得到的振动台面加速度激励施加于带力测量工装的卫星结构有限元模型,可以计算得到力测量工装处的传递动载荷;利用得到的六个力传感器位置处载荷时程进一步计算振动台与卫星结构之间传递的六自由度动载荷,验证界面传递六自由度载荷识别结果的精度。由于振动台加速度激励为沿x方向的水平激励,六自由度载荷中,沿x方向的水平合力与绕y轴方向的弯矩为主要的载荷成份。图14和图15中分别给出了正弦激励和正弦扫频激励下x,y方向合力以及绕y轴弯矩的识别值与试验参考值之间在某一个时段的对比结果。结果表明:识别得到的界面动载荷均具有良好的精度,证明了本文提出的界面动载荷识别方法的有效性。正弦激励工况中三个动载荷识别值与试验值峰值误差分别为0.923 8,0.082 9,0.016 1;扫频激励工况中三个动载荷识别值与试验值峰值误差分别为0.705 9,0.326 3,0.129 4。图中显示载荷识别值与参考值之间存在一定的相位差,可能的原因是力传感器测量信号存在大量噪声,滤波后存在相位漂移,通过提高力信号测量精度有望实现更小的识别误差。
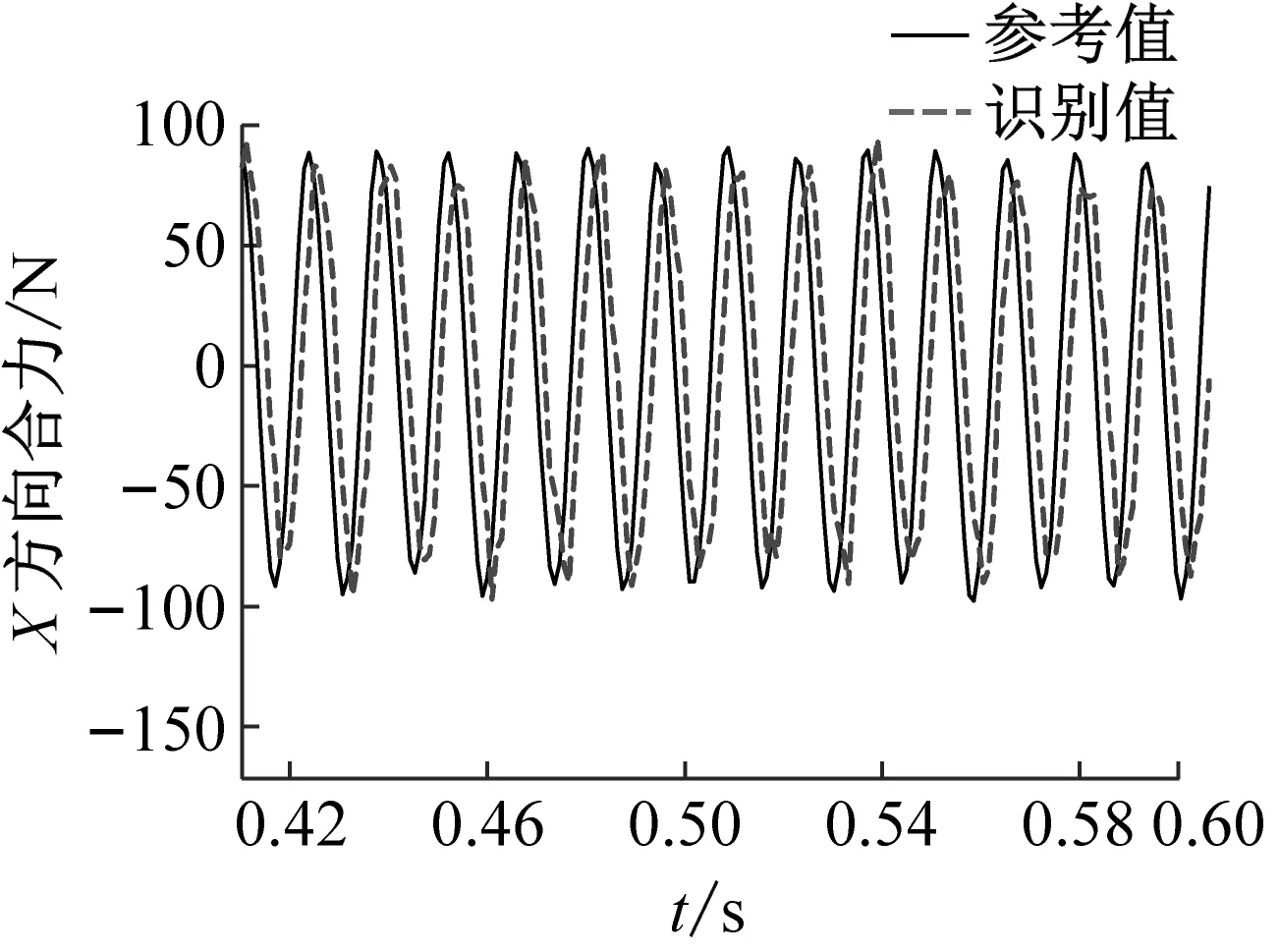
(a) x方向合力
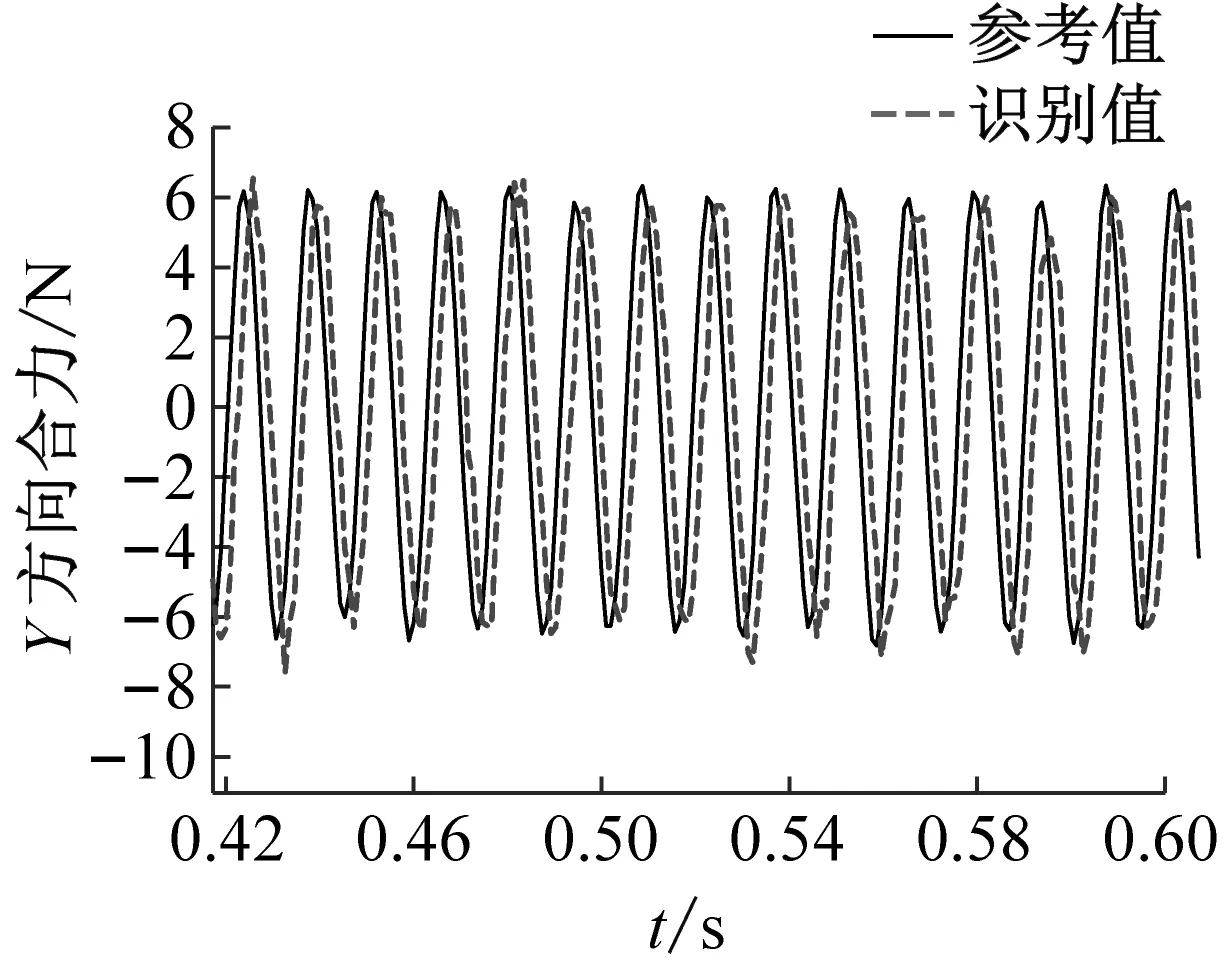
(b) y方向合力
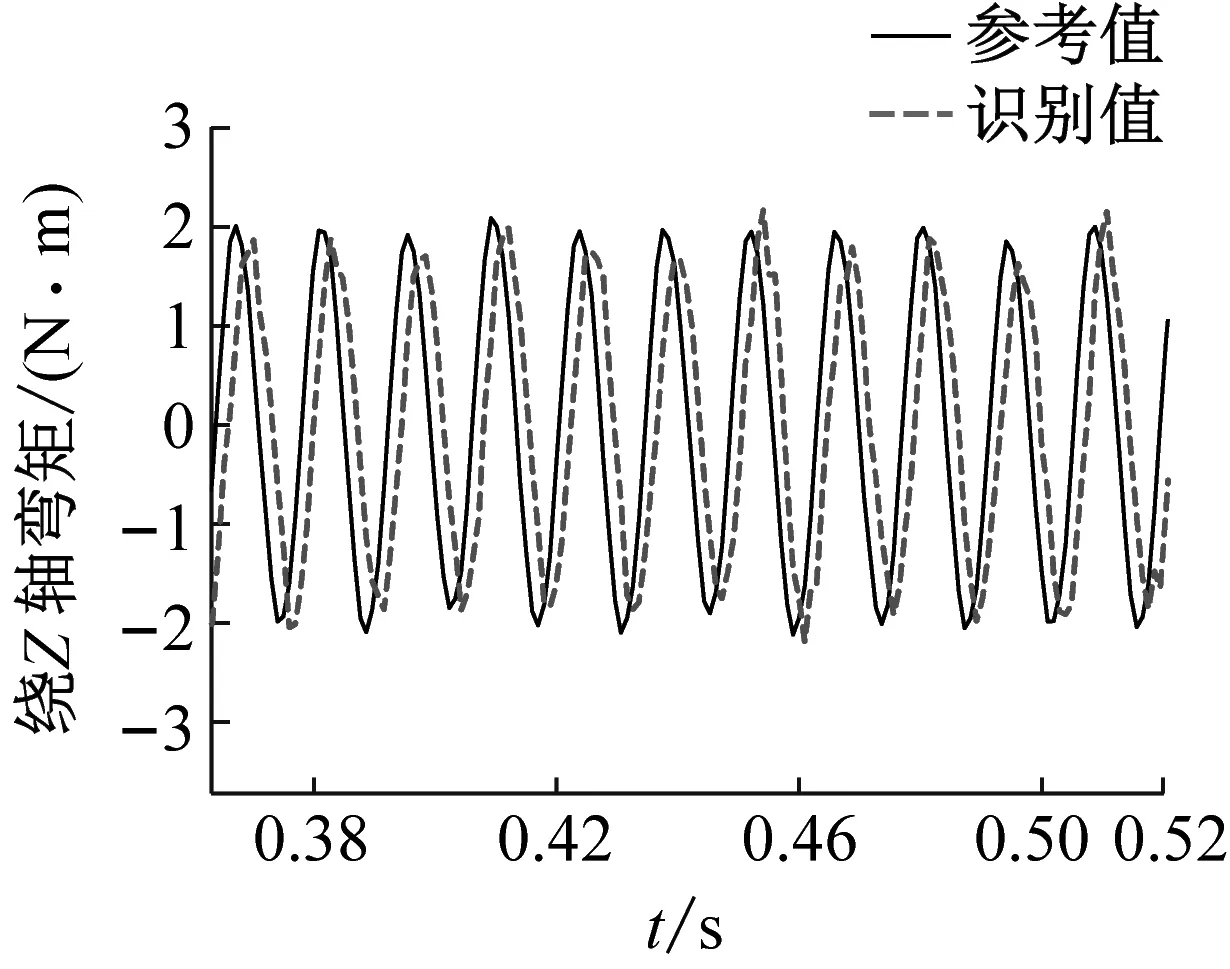
(c) 绕z轴弯矩图14 正弦激励下部分六自由度动载荷识别值与实测值对比Fig.14 Comparison of the identified and measured partial six degree-of-freedom dynamic load under sinusoidal excitation
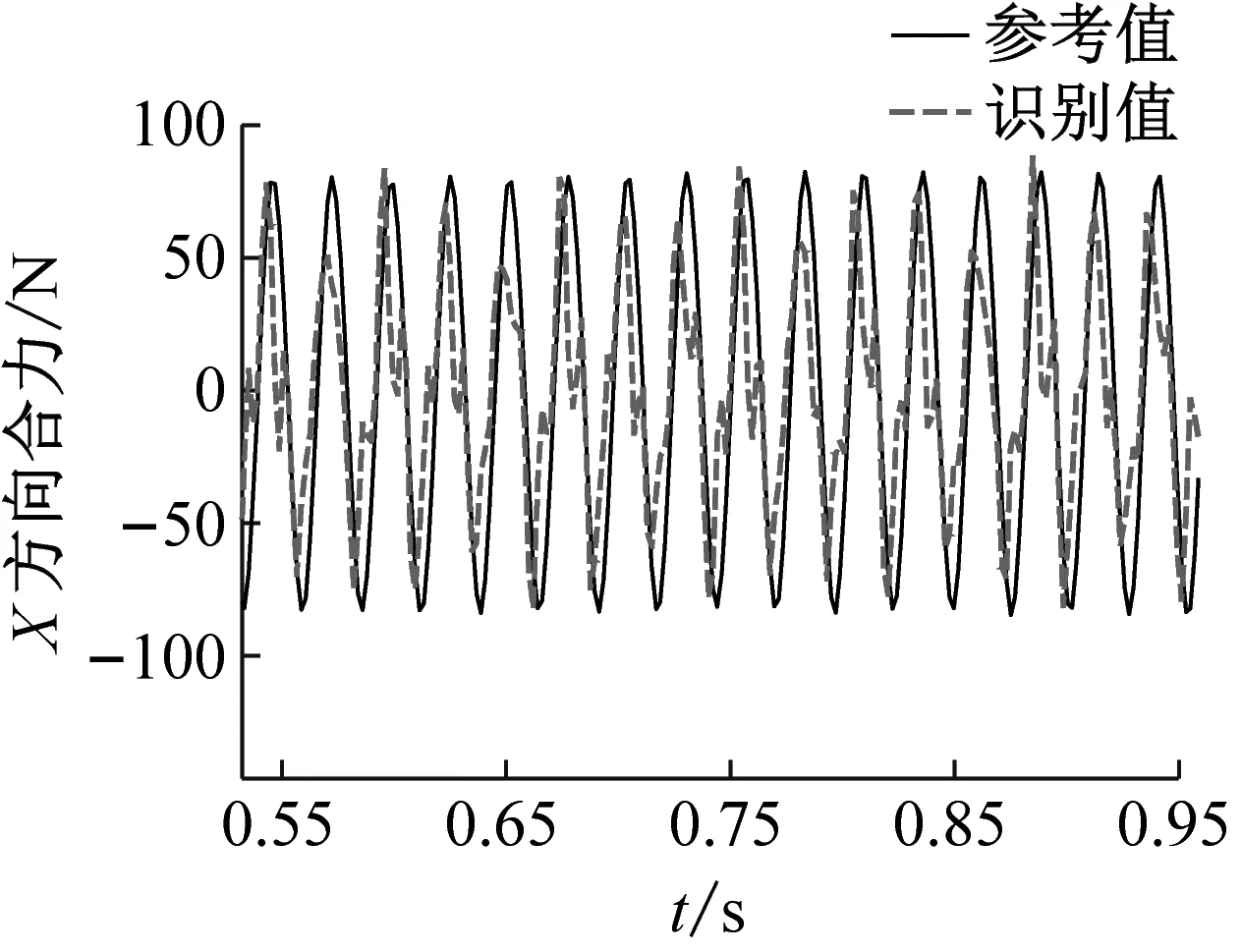
(a) x方向合力
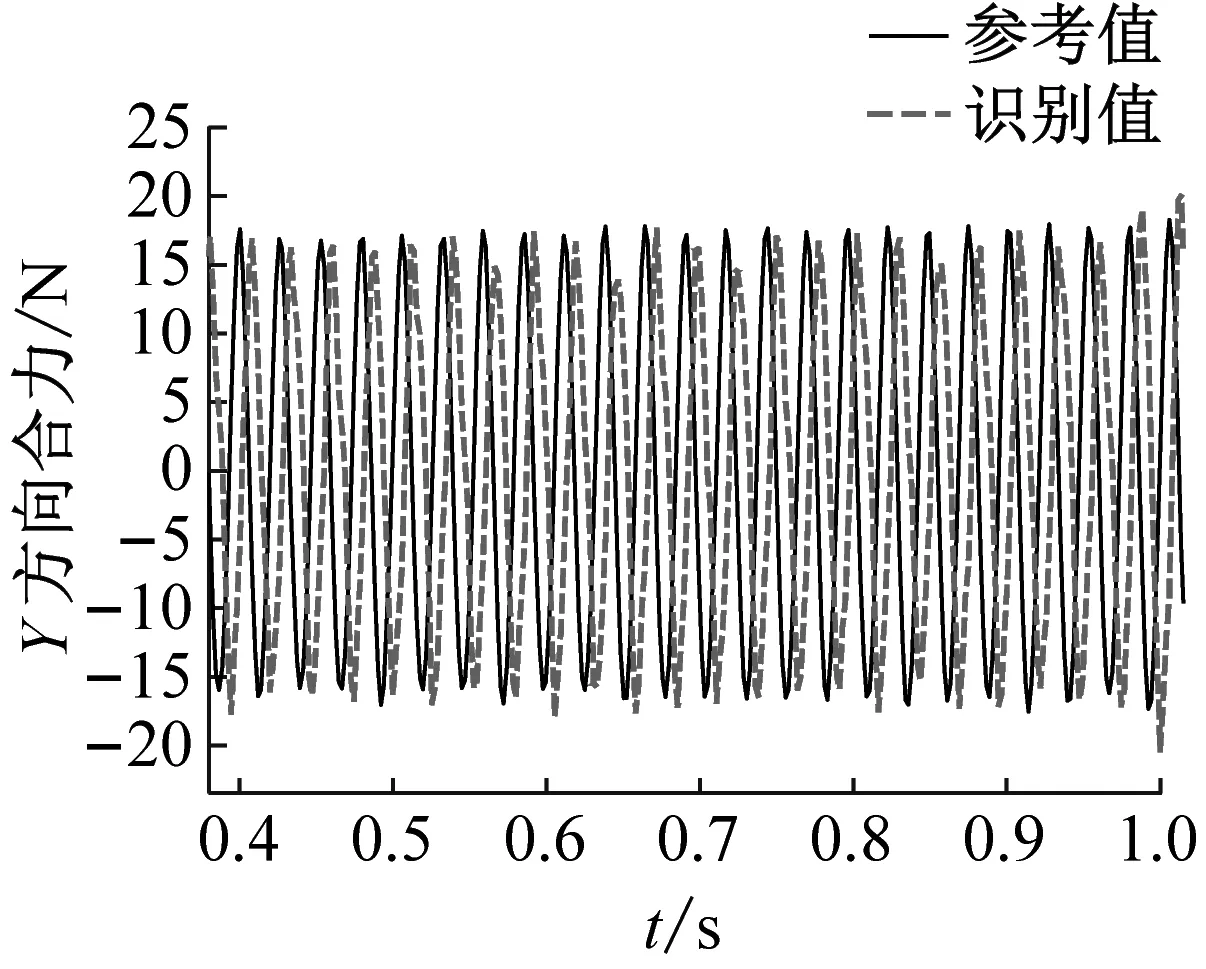
(b) y方向合力
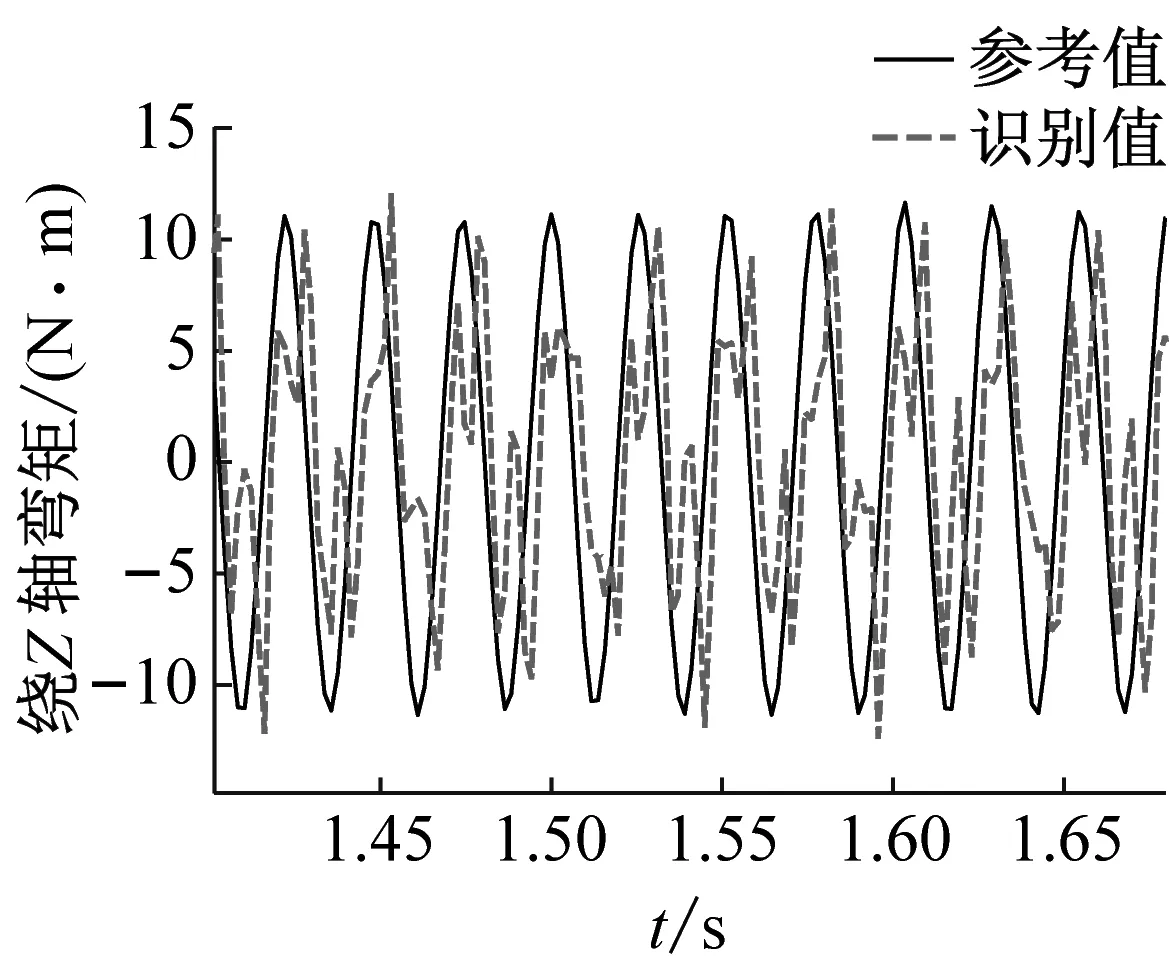
(c) 绕z轴弯矩图15 正弦扫频激励下部分六自由度动载荷识别值与实测值对比Fig.15 Comparison of the identified and measured partial six degree-of-freedom dynamic load under swept-sin excitation
4 结 论
本文基于卫星结构加速度响应和星箭界面加速度激励构建了激励-响应样本数据库,利用BP神经网络训练界面处加速度激励-卫星结构加速度响应间的传递关系,从而建立了星箭界面处加速度激励的识别模型,并进一步将识别得到的加速度激励施加于高保真卫星结构有限元模型,实现了基于BP神经网络模型的星箭界面动载荷的识别。开展了仿真和试验研究,验证了方法的有效性。主要结论如下:
(1) 利用激励-响应样本库建立的神经网络训练模型能够准确的反演卫星结构基础加速度激励,该方法具有良好的噪声鲁棒性。利用反演得到的基础加速度激励和卫星结构有限元模型,能够准确预测星箭界面动载荷。
(2) 用于动载荷识别的神经网络模型训练中,样本库构建至关重要;基于宽频随机振动工况下的激励-响应样本库构建的神经网络模型的普适性更好,能够高精度完成定频正弦激励的识别,反之则不能。
(3) 卫星发射过程中,星箭对接面附近的加速度和卫星结构局部加速度响应均可测,本文的方法有望实现服役状态下的星箭界面动载荷预测。
