刚性弓网系统参数对接触线波磨的影响研究
2023-03-20李先航陈光雄梅桂明何俊华刘达毅冯晓航
李先航, 陈光雄, 梅桂明, 何俊华, 刘达毅, 冯晓航
(1.西南交通大学 机械工程学院 摩擦学研究所,成都 610031;2.西南交通大学 牵引动力国家重点实验室,成都 610031)
截至2020年底,我国内地已经开通城轨交通线路长度7 969.7 km,其中地铁占78.81%[1]。地铁以自身运量大、准时、乘坐舒适等特点成为了城轨交通的主要方式。刚性悬挂接触网因其结构简单、维护方便、无张力、低电阻等特点被普遍使用在地铁隧道中[2-3]。虽然刚性接触网具备众多优点,但也发现刚性接触网系统的滑板和接触线异常磨损严重,而且很多接触线出现了局部波磨问题[4]。接触线局部波磨与现阶段刚性接触网滑板和接触线的异常磨耗有无关系尚缺乏深入的认识,但接触线波磨肯定恶化了弓网接触关系,影响到弓网系统的受流质量。当弓网系统出现波磨时,受电弓与接触线之间因接触损耗而产生的电弧会相继出现,导致接触线和受电弓滑板材料的过度磨损,严重时会导致供电中断,增加地铁列车非正常停车的风险。
对于架空刚性接触网,接触线波磨形成的完整机理尚未阐明,因此研究其机理并获得减缓或抑制接触线波磨的措施具有重要意义。Koyama等[5-6]研究了架空刚性接触网接触线表面状态和受电弓的动态特性,认为受电弓的动态特性导致接触线波磨,特别是受电弓的反共振现象对这一过程影响显著。Aboshi等[7]进行了受电弓实际线路磨损特性的研究和激励试验,他认为接触线波磨的机理是:受电弓与接触线之间的接触力波动导致最初微小不均匀磨耗的形成,只有当它的波长等于能引起波动磨损的波长之一时幅值才会增大,最后通过接触损耗弧使不均匀度迅速增大。Mandai等[8]证实了接触线波磨会影响到刚性弓网系统动力特性,会使刚性弓网磨损速率变快,并提供了一种能够减少接触线波磨的打磨装置,从而减轻了接触线的波磨。钱世勇等[9]对成都地铁线路刚性弓网系统动态性能进行了实测,他认为弓头剧烈振动会使接触力波动范围变大,加剧刚性接触网的波形磨耗。盛良等[10]根据地铁线路观测和运营工区统计数据发现接触线波磨主要集中在出站加速区段,波磨由暗亮带交替组成且较严重,他认为波磨是电流、接触力和电弧相互作用引起的结果。谭冬华[11]研究表明波磨是接触线相对于碳滑板中心偏移值分布不合理引起的,使中心偏移值分布密度大致服合正态分布能有效缓解波磨。
以往的研究者在研究刚性接触网接触线波磨时,很少从弓网系统内部激励的角度来进行研究。近几年,Chen等[12-16]课题组利用复特征值法来研究轮轨系统中的摩擦自激振动现象及钢轨波磨问题并取得了较多成果。本文作者从摩擦学角度,基于摩擦自激振动引起波磨理论,利用复特征值方法研究刚性弓网参数对接触线波磨的影响。研究表明选择合适的刚性弓网参数可以减缓或显著减轻接触线波磨。
1 刚性弓网系统有限元模型和理论方法
1.1 刚性弓网系统有限元模型
刚性弓网系统有限元模型如图1所示。受电弓位于刚性接触网的中间位置,整个模型均为六面体实体单元(C3D8I),网格数量总共为333 655个。碳滑板与接触线接触部分引入了摩擦耦合,在这个模型中,受电弓碳滑板与接触线的接触是模型中的重要部分,为了提高计算精度,接触线与碳滑板接触部分均细化,刚性弓网系统接触细节如图2所示。受电弓各部件材料属性如表1所示[17-18]。受电弓底座固定,模型中可以转动的部分均由销连接,忽略转动销的摩擦力,下臂杆底部扇形板施加升弓力,每个弓头支架安装两个扭簧,吸收高频振动。刚性接触网材料属性如表2所示[19-21]。

图1 刚性弓网系统有限元模型Fig.1 Finite element model of pantograph-rigid catenary system

图2 刚性弓网系统接触细节Fig.2 Contact details of pantograph-rigid catenary system

表1 受电弓各部件材料属性Tab.1 Material properties of the pantograph component
表2 刚性接触网材料属性Tab.2 Material properties of the rigid catenary
接触网总长度为50 m,跨距为12 m,悬挂机构为4个。地脚螺栓上端施加固定边界条件,由于定位线夹将汇流排夹紧,汇流排将接触线夹紧,整个接触网基本无相对运动,因此将整个接触网进行了合并。
1.2 刚性弓网系统摩擦自激振动理论方法
本文利用ABAQUS软件中复特征值法对刚性弓网系统摩擦自激振动进行研究。在存在摩擦的情况下,受电弓与刚性接触网的彼此作用是十分复杂的,其复杂性集中于碳滑板与接触线之间的摩擦耦合。ABAQUS软件中以Yuan[22]的方法添加两个弹性体之间的摩擦耦合。摩擦系统自激振动建模简要介绍如下:在不考虑外力和摩擦力的情况下,建立如下系统动力学方程

(1)
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;x为位移矢量。M、C、K均为对称矩阵,此时方程(1)特征方程不可能出现实部大于0的特征值,即系统是稳定的。加入摩擦耦合后,系统动力学方程转变成
(2)
式中:Mr为化简后的质量矩阵;Cr为化简后的阻尼矩阵;Kr为化简后的刚度矩阵。对方程(2)进行求解得
(3)
式中:βk+ωkj为系统特征值;βk为特征值实部;ωk为特征值虚部;φk为特征向量;t为时间。由于Mr、Cr、Kr均为非对称矩阵,因此βk大于0,x(t)随t呈指数增大,表明刚性弓网系统的振动将变得不稳定。通常使用等效阻尼比ζk来评估刚性弓网系统的稳定性,定义如下
(4)
当ζk小于0时,ζk越小,刚性弓网系统产生摩擦自激振动的可能性也就越大即越容易出现接触线波磨。
2 计算结果分析
2.1 预测结果与实测接触线波磨的对比
当等效阻尼比ζk≥-0.001时,摩擦系统对应的不稳定振动不太可能发生,可不考虑[22]。在摩擦因数μ=0.3、法向接触力F=120 N、弓头悬挂扭簧刚度K=26 N·m/rad、跨距L=12 m、滑动速度v=60 km/h的条件下[23-25],在0~1 000 Hz内,刚性弓网系统于频率f=51.97 Hz、818.01 Hz、918.78 Hz发生摩擦自激振动现象。刚性弓网系统不稳定振动模态如图3所示,从图3(a)、(b)、(c)中可以看出频率为f=51.97 Hz接触网、碳滑板、平衡杆中均出现明显的振动,频率为f=818.01 Hz、918.78 Hz振动主要出现在碳滑板及弓头支架,虽然频率f=818.01 Hz对应的等效阻尼比并不是最小,但是一些研究发现摩擦自激振动有时会在等效阻尼比较大时发生[26]。由此推知频率为f=818.01 Hz可能为刚性弓网系统摩擦自激振动导致接触线波磨出现的频率。
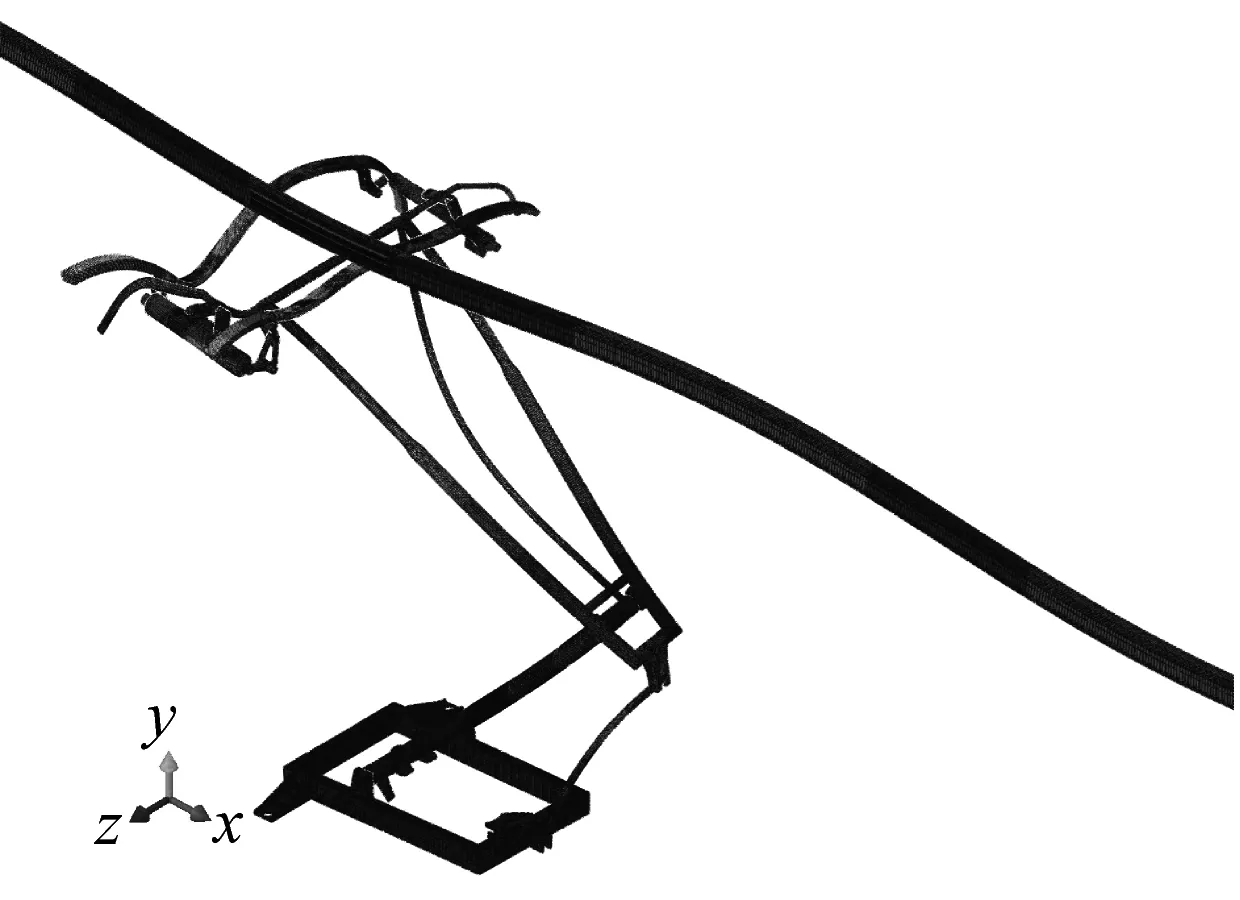
(a) f=51.97 Hz,ζ=-0.009 94
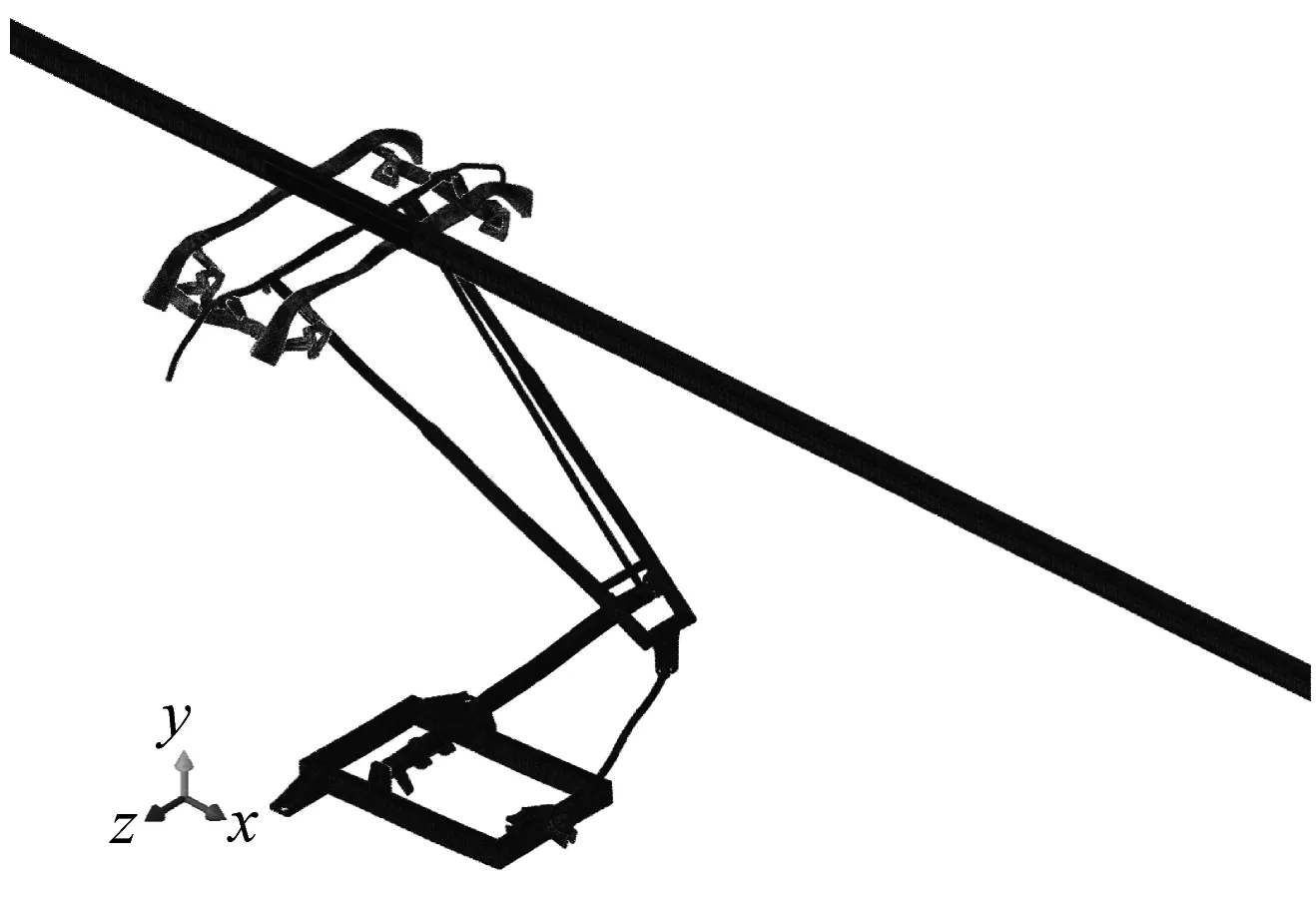
(b) f=818.01 Hz,ζ=-0.005 11
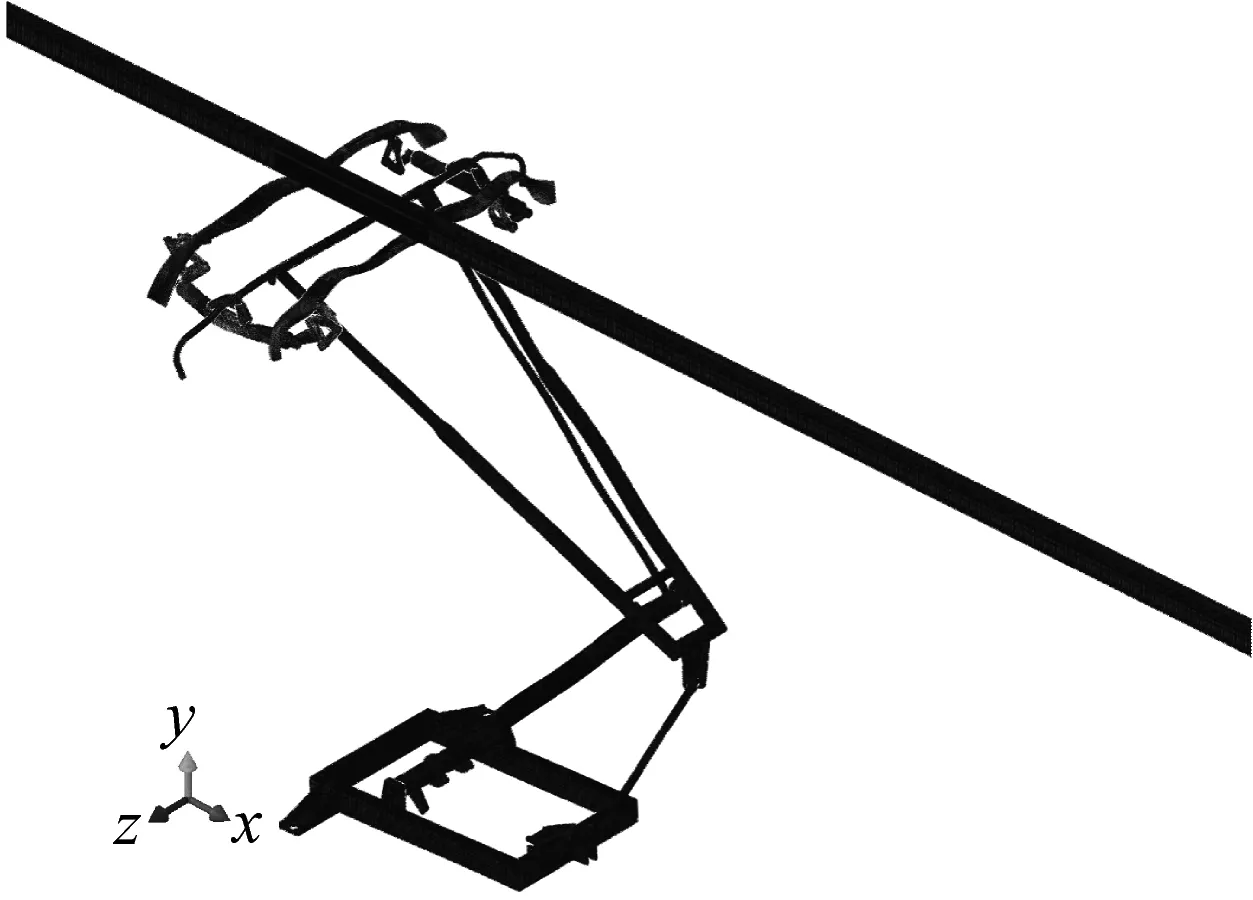
(c) f=918.78 Hz,ζ=-0.001 16图3 刚性弓网系统不稳定振动模态Fig.3 Unstable vibration mode shapes of the pantograph-rigid catenary system
在发生接触线波磨的地段,地铁行车速度v约为60 km/h。根据本文的预测,接触线的波磨波长λ为:λ=60/3.6/818.01=0.020 4 m=20.4 mm,实际接触线波磨如图4所示,其波长约为20 mm,两者十分接近。说明此模型用来预测接触线波磨基本正确。

图4 接触线波磨照片Fig.4 Photo of contact wire corrugation
2.2 摩擦因数对接触线波磨的影响
黄之元[23]在载流摩擦磨损试验机试验结果显示,地铁同种摩擦副在低速载流不同工况下摩擦因数约为0.25~0.36。在法向接触力F=120 N,弓头悬挂扭簧刚度K=26 N·m/rad,跨距L=12 m,滑动速度v=60 km/h的计算条件下,刚性弓网系统在不同摩擦因数下,等效阻尼比ζ和频率f的变化关系如图5所示,刚性弓网系统在不同频率下,等效阻尼比ζ和摩擦因数μ的变化关系如图6所示。当摩擦因数μ小于0.15时,无负等效阻尼比,此时刚性弓网系统是稳定的。从图5中可以看出随着摩擦因数从0.15增加至0.60,刚性弓网系统出现的负等效阻尼比个数逐渐从1增加至4。从图6中可以看出,随着摩擦因数从0.15增大至0.60,刚性弓网系统均出现频率f=818.01 Hz的不稳定振动且频率f=51.97 Hz、64.48 Hz、818.01 Hz的等效阻尼比均逐渐减小。从图5、图6分析可知随着摩擦因数的增大,摩擦自激振动越强烈,接触线波磨越容易发生,这是因为摩擦力随着摩擦因数的增大而增大,摩擦耦合作用随着摩擦力的增大而增强。
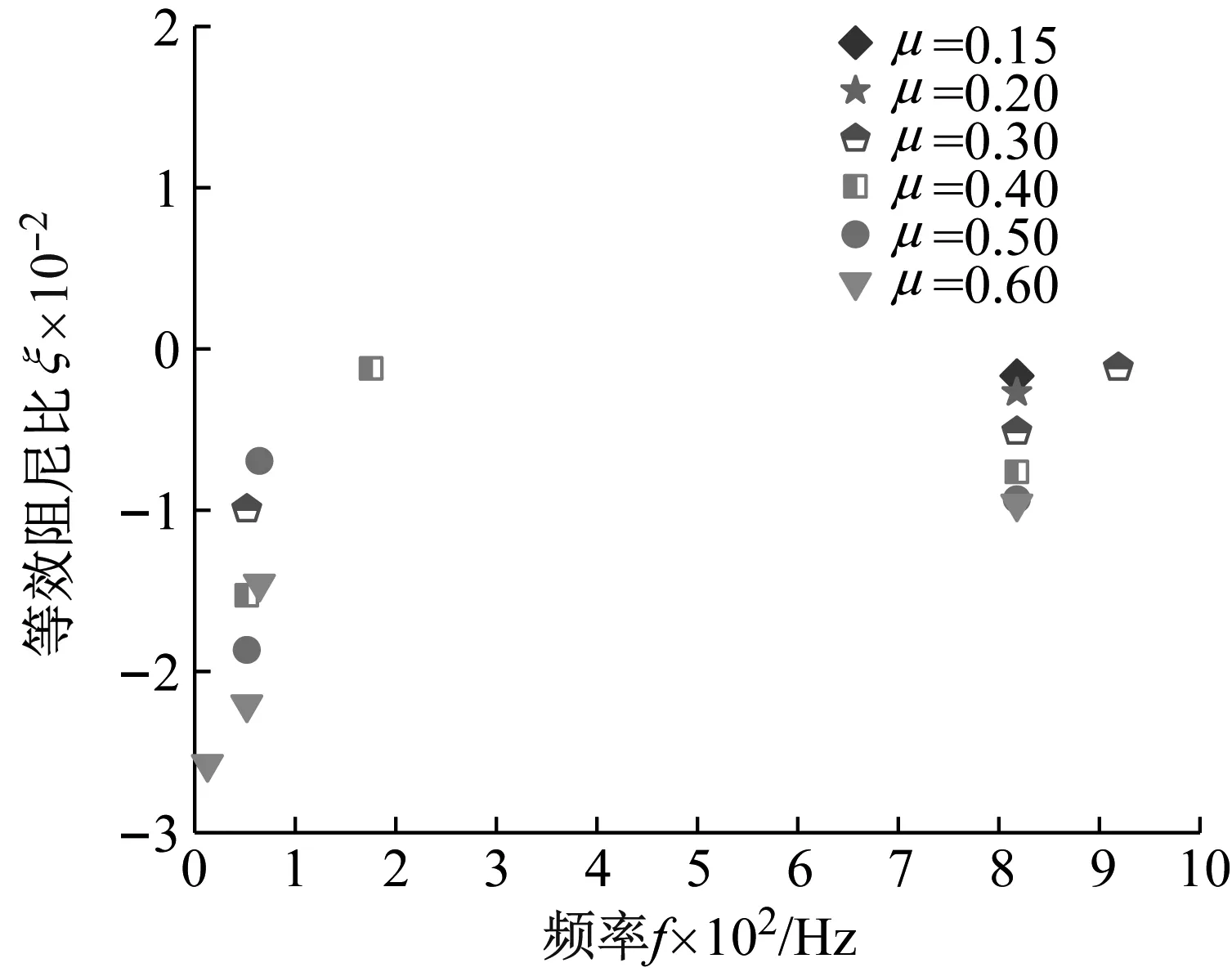
图5 不同摩擦因数下,等效阻尼比ζ和频率f的变化关系Fig.5 Under different friction coefficients, the variation of the effective damping ratio ζ with frequency f

图6 不同频率下,等效阻尼比ζ和摩擦因数μ的变化关系Fig.6 Under different frequencies, the variation of the effective damping ratio ζ with friction coefficient μ
2.3 法向接触力对接触线波磨的影响
在摩擦因数μ=0.3,弓头悬挂扭簧刚度K=26 N·m/rad,跨距L=12 m,滑动速度v=60 km/h的计算条件下,刚性弓网系统在不同频率下,等效阻尼比ζ与法向接触力F的变化关系如图7所示。从图7中可以看出随着法向接触力F从10 N增加至110 N,刚性弓网系统仅出现1~2个负等效阻尼比,且两个等效阻尼比均较大;当法向接触力F从120 N增加至180 N时,负等效阻尼比个数为3~5个,此时刚性弓网系统变得较不稳定,摩擦自激振动较强烈,接触线波磨也较强烈。这是因为摩擦力随着法向接触力的增大而增大,摩擦耦合作用得到加强。

图7 不同频率下,等效阻尼比ζ与法向接触力F的变化关系Fig.7 Under different frequencies, the variation of the effective damping ratio ζ with normal contact force F
2.4 弓头悬挂扭簧刚度对接触线波磨的影响
在摩擦因数μ=0.3,法向接触力F=120 N,跨距L=12 m,滑动速度v=60 km/h的计算条件下,刚性弓网系统在不同频率下,等效阻尼比ζ与弓头悬挂扭簧刚度K的变化关系如图8所示。从图8中可以看出当扭簧刚度K从10 N·m/rad增加至30 N·m/rad,刚性弓网系统出现2~3个负等效阻尼比;当扭簧刚度K从40 N·m/rad增加至90 N·m/rad时,出现2个负等效阻尼比;当扭簧刚度K增大至100 N·m/rad时,只出现1个负等效阻尼比且等效阻尼比较大。说明刚性弓网系统此时较稳定,这是因为弓头悬挂扭簧有效缓解了刚性弓网系统摩擦自激振动,接触线波磨发生的可能性减小。

图8 不同频率下,等效阻尼比ζ与弓头悬挂扭簧刚度K的变化关系Fig.8 Under different frequencies, the variation of the effective damping ratio ζ with stiffness K of pantograph-head suspension torsion spring
2.5 跨距对接触线波磨的影响
在摩擦因数μ=0.3,法向接触力F=120 N,弓头悬挂扭簧刚度K=26 N·m/rad,滑动速度v=60 km/h的计算条件下,刚性弓网系统在不同跨距下,等效阻尼比ζ与频率f的变化关系如图9所示。从图9中可以看出当跨距L=6 m时刚性弓网系统只出现1个负等效阻尼比且较大;当跨距L=8 m、10 m时刚性弓网系统均出现2个负等效阻尼比;当跨距L=12 m时刚性弓网系统出现3个负等效阻尼比,因此当跨距L=6 m时刚性弓网系统较稳定。这是因为跨距的减小增强了接触网的稳定性,摩擦自激振动得到减缓,接触线波磨得以有效减缓。
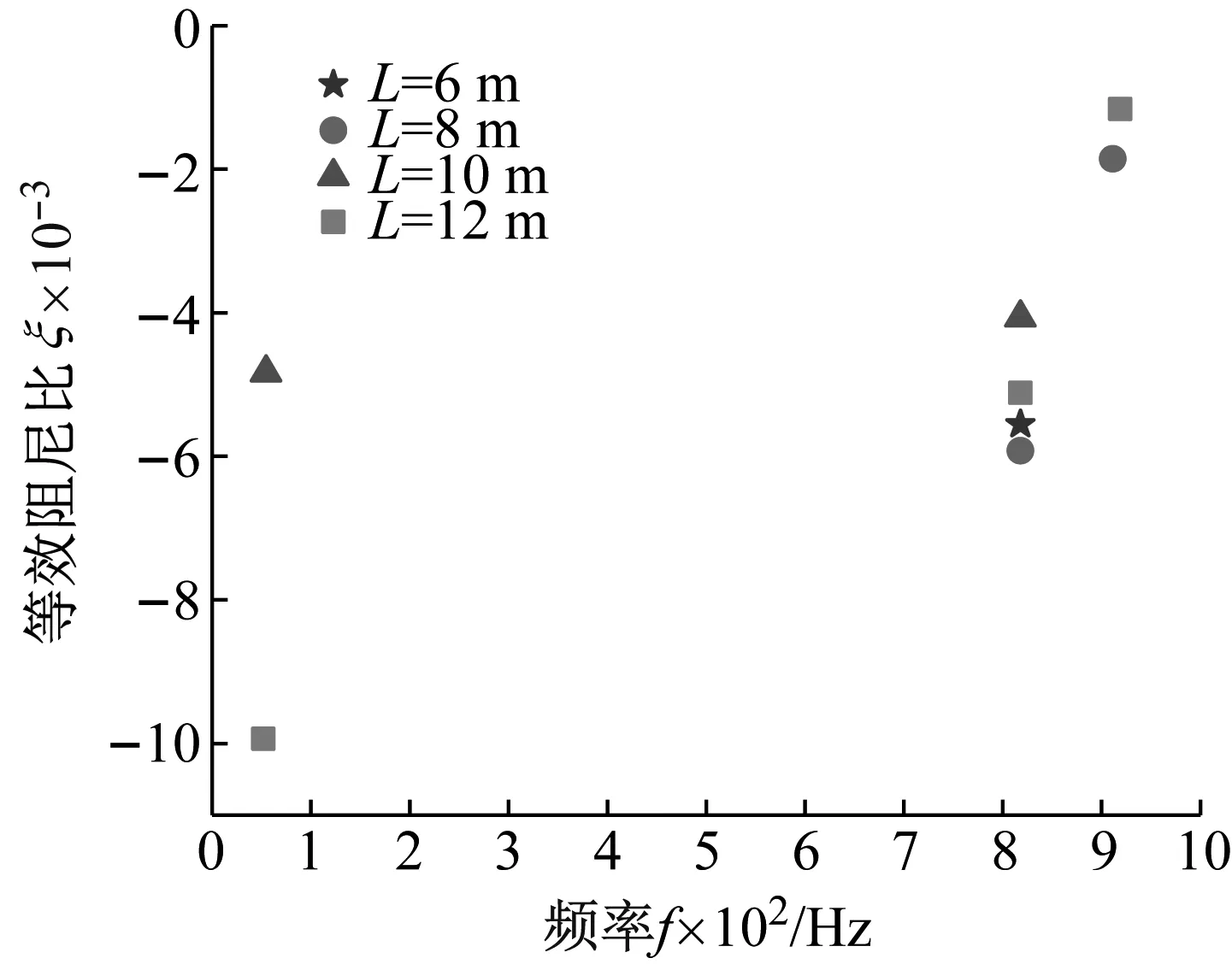
图9 不同跨距下,等效阻尼比ζ与频率f的变化关系Fig.9 Under different spans, the variation of the effective damping ratio ζ with frequency f
3 结 论
(1) 当摩擦因数μ≥0.15时,刚性弓网系统可能发生摩擦自激振动导致接触线波磨。摩擦因数越大,摩擦自激振动越容易出现,减小摩擦因数μ至0.15以下可以显著减轻接触线波磨。
(2) 较大的法向接触力容易导致刚性弓网系统产生摩擦自激振动。减小法向接触力至110 N以下可以有效缓解接触线波磨。
(3) 刚性弓网系统的稳定性随着弓头悬挂扭簧刚度的增加而增大。当弓头悬挂扭簧刚度增大至100 N·m/rad时,接触线波磨发生的可能性较小。
(4) 刚性弓网系统的稳定性随着跨距的减小而增强。当跨距减小至6 m时,接触线波磨得到有效缓解。
