框架-分布摇摆芯筒-核心筒结构体系力学模型及耗能减震性能分析
2023-03-20陈易飞何浩祥兰炳稷孙澔鼎
陈易飞, 何浩祥, 兰炳稷, 孙澔鼎
(北京工业大学 工程抗震与结构诊治北京市重点实验室,北京 100124)
随着经济和科技水平的发展,高层建筑结构的数量日益增多,形式趋于多样化且设计水平也不断提高[1-2]。框架-核心筒(Frame-core tube,FCT)结构体系是目前高层建筑中应用较为广泛的一种形式,该结构由框架和核心筒组成了双重抗侧力体系,核心筒因刚度较大作为第一道抗震防线,而外围框架则作为第二道防线[3],FCT结构体系示意图如图1(a)所示。

图1 结构体系示意图Fig.1 Schematic diagram of structure system
在进行FCT结构抗震设计时,为了提高整体抗侧刚度,设计者通常会适当增大核心筒的围合面积占比。然而,由于框架才是使用者的主要活动场所,上述设计理念会因过分注重结构安全储备而削弱了适用性和经济性。提升FCT结构经济性的直接途径便是减小核心筒的围合面积,但是该方法必然会削弱结构的抗震性能。根据结构布置宜采取多道防线的设计理念[4],可考虑在FCT结构中增设一道抗震防线以提高结构安全性能。近年来,部分研究者建议将FCT结构中的核心筒改设为若干子筒,通过构造措施将各子筒之间通过结构构件或者耗能装置相连,使结构具备构件或者耗能装置、子筒和框架三道抗震防线[5-6]。但该设计方法是将核心筒在原位置上进行拆分,并没有真正实现筒体围合面积的减小。借鉴分散筒结构体系的设计理念[7],本文建议可将传统FCT结构体系的核心筒围合面积进行缩小,同时在框架部分内均匀布置若干分布芯筒,形成框架-分布芯筒-核心筒(frame-distributed tubes-core tube,FDCT)新型高层结构体系。新体系的筒体总围合面积要小于传统FCT结构的核心筒围合面积,其构体系示意图如图1(b)所示。FDCT结构形成了包括分布芯筒、核心筒及框架三道防线的三重抗侧力体系,附加的分布芯筒对各子结构的抗震能力进行协调,而核心筒围合面积的减小,可改善传统FCT结构中核心筒刚度与框架相比悬殊较大在强震作用下出现过早屈服而对结构造成抗震不利的影响[8];各筒体总围合面积占比的减小增加了结构的经济性,同时芯筒的分散布置也可提高结构布局的灵活性。
高层建筑在水平荷载作用下会发生侧向位移并产生薄弱层破坏,由于FDCT结构的核心筒刚度相对较小,其薄弱层的破坏可能会更加严重。在结构中加入刚度较大的摇摆构件能有效地改变结构变形模式,抑制薄弱层的出现,减小地震响应[9]。对结构附加摇摆构件的研究中,大多采用将框架结构与具有摇摆功能的剪力墙和填充墙等构件相结合的方式,相关研究表明附加摇摆构件可有效实现对框架结构的损伤控制,使其变形更加均匀,提高其抗震能力[10-12]。在摇摆体系与核心筒相结合方面,Meek[13]较早提出了摇摆核心筒结构,并采用简化单自由度模型对不同高宽比的摇摆核心筒结构进行了分析。Nielsen等[14]对核心筒基础固接与摇摆核心筒两种形式进行了强震下性能对比分析,结果表明摇摆核心筒可以有效减小结构基底弯矩。
为了进一步提高框架-分布芯筒-核心筒结构体系抗震能力,控制结构损伤模式,提高结构变形均匀程度并减小薄弱层破坏,基于摇摆体系理念,本文认为可将具有足够大刚度的分布芯筒与摇摆体系相结合,形成框架-分布摇摆芯筒-核心筒(frame-distributed rocking tubes-core tube,FDRCT)新型高层结构体系,该体系的示意图如图1(c)所示。本文将以FCT结构、FDCT结构和FDRCT结构为研究对象,以提高经济性为基础分别设定三种结构的参数,从力学机制出发,建立各体系简化分析模型,基于Lagrange方程和动量矩定理建立各体系运动方程,通过动力分析分别求解并对比不同结构的地震响应,之后对各个结构在不同场地以及不同类型长周期地震波下的抗震能力进行对比分析。最后,根据三种结构在不同类型地震波下性能-利润总值的对比,验证FDRCT结构在经济性和抗震减震能力两方面同时具备优势。
1 FDCT结构体系运动方程
1.1 简化分析模型
根据传统FCT结构体系的构造形式以及工作原理可将其简化为如图2(a)所示的分析模型,其中结构中部的核心筒可简化为一个底端固定的悬臂梁,将框架的每层等效为一个集中质量,核心筒和框架之间通过连梁进行刚性连接。

图2 结构简化分析模型Fig.2 The simplified analytical model of structure system
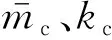
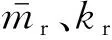
1.2 动力方程推导
考虑到以上高层结构体系受力复杂,在建立运动方程时结构的惯性力和弹性恢复力形式也较繁复,而Lagrange方程在运用过程中可不必直接分析上述因素,是完全的标量分析方法,因此本文运用Lagrange方程对以上三种结构体系进行运动方程的相关推导。由于FDRCT结构相对于FCT结构和FDCT结构工作机理较为复杂,其受力分析也最为全面,限于篇幅,本文仅阐述FDRCT结构的动力方程的推导过程,其它体系动力模型的建立方法是类似的。结构中的核心筒在简化分析模型中被等效为一端固接的悬臂梁,因此,其筒体上任意一点z在t时刻相对于地面的水平位移为[15]
uc(z,t)=qc(t)φc(z)
(1)
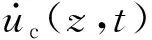
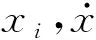
(2)
式中:T为结构体系的动能;V为结构体系的势能;qi为结构体系中各子结构的广义坐标,本文中qi包括qc、xi和θ,Qqi为对应广义坐标qi的广义力。
FDRCT结构体系的动能可表示为
(3)

FDRCT结构体系的势能为
(4)
式中,假设在实际工程中受到外部激励的分布摇摆芯筒在摇摆过程中的转角θ不会大于5°,因此其水平位移分量可用zisinθ进行计算。
FDRCT结构体系中存在非保守力做功,其包括地震惯性力以及阻尼力,设结构体系的虚位移为δqc,δxi,δθ,则地震力所做的虚功为
(5)

阻尼力作做的虚功为
(6)
根据式(5)和(6)得到广义坐标qc、xi和θ所对应的广义力Qqc,Qxi和Qθ,联立式(3)和(4)并代入到(2),可得到FDRCT结构体系关于核心筒相对于地面水平位移的运动方程
(7)
由于分布摇摆芯筒转角θ小于5°,在以下推导过程中将sinθ≈θ,cosθ≈1,关于框架中位移x1的运动方程为
(8)
关于框架中位移xi(i为2~n-1)的运动方程为:
[(ki+ki+1)+(kcbi+krbi)]xi-k1xi-1-
(9)
关于框架中位移xn的运动方程为
(10)
关于分布摇摆芯筒转角的运动方程为
(11)
综上,根据式(7)~(11)可得到FDRCT结构体系的质量矩阵、刚度矩阵、阻尼矩阵以及外荷载矩阵,进而推导出相应的状态空间表达式,最终可采用Runge-Kutta方法实现方程组的时域求解及结构动力时程分析。
2 结构体系地震响应分析
2.1 结构信息
为了进一步研究FDCT结构体系和FDRCT结构体系相对于传统FCT结构体系的抗震性能,本文设计了三种结构的分析模型并对其进行数值模拟。参考文献[16]的结构模型,设计了一栋25层总高为100 m的FCT结构,其结构典型楼层示意图如图3(a)所示。在此结构基础之上,将中部核心筒围合面积进行相应缩小,并在核心筒与外围框架对角连线中部分别布置了四个围合面积较小的分布芯筒,形成FDCT结构,结构典型楼层示意图如图3(b)所示。FDRCT结构是在FDCT结构基础之上将分布芯筒基底加入铰接机制,同时与分布芯筒相连接的框架梁两端也均需设置铰接节点,使分布芯筒在地震作用下可发生充分的摇摆,其它结构信息均与FDCT结构相同。为了满足FDRCT结构中摇摆体系的工程可行性,Qu等的摇摆墙齿状铰支座以及文献[17]提出的弯曲耗能铰,设计了分布摇摆芯筒基底所使用的双向齿状铰支座和铰接节点所使用的铰接装置,分别如图4(a)和4(b)所示。双向齿状铰支座通过刚性支撑与分布摇摆芯筒相连,支座下齿宽度大于上齿宽度,从而防止摇摆过程中发生脱落。上齿与下齿的咬合处均可做圆滑处理,确保摇摆功能的实现。在正常使用中梁端弯曲耗能铰具有足够的刚度,在地震时则可触发铰接机制,使梁端具备转动能力。开孔软钢既可为梁端提供刚度,又可在地震时率先进入屈曲状态并耗能。
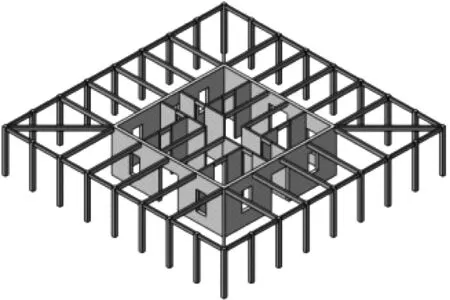
(a) FCT结构
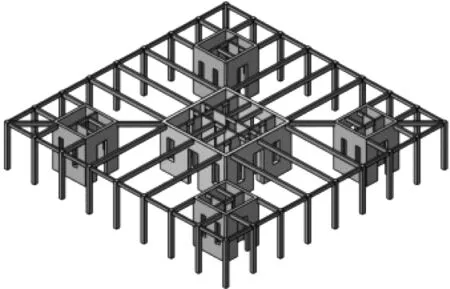
(b) FDCT结构图3 结构典型楼层三维示意图Fig.3 The 3D schematic diagram of the typical floor

(a) 基底铰接装置

(b) 梁端铰接装置图4 铰接装置构造图Fig.4 Structural diagram of hinged devices
FCT结构模型与FDCT结构模型平面图分别如图5(a)及图5(b)所示。结构共25层,总高为100 m,层高为4 m,结构平面尺寸为40 m×40 m。FCT结构的核心筒尺寸为20 m×20 m,其围合面积占结构面积的25%;而为了提高结构经济性,将FDCT结构核心筒尺寸设为12 m×12 m,单个分布芯筒的尺寸为6 m×6 m,其筒体总围合面积仅占结构总面积的18%。结构位于8度抗震设防区,场地类别为Ⅲ类,设计地震分组为第1组。
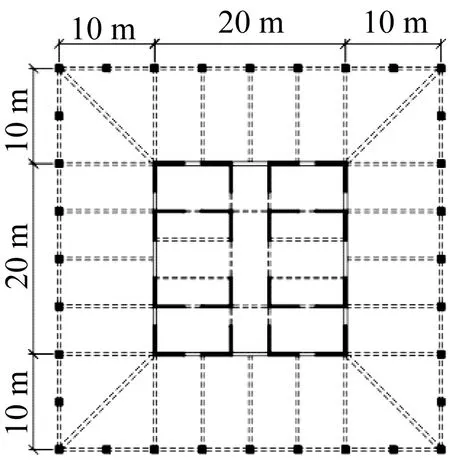
(a) FCT结构

(b) FDCT结构图5 结构平面图Fig.5 Structural plan
FDCT结构和FDRCT结构的简化分析模型参数需要在FCT结构基础之上改设,其中FCT结构模型的主要构件信息为:圈梁为250×550 mm,角梁为400×850 mm,连系梁为300×700 mm,1~7层柱为750×750 mm,8~16层柱为700×700 mm,17~25层柱为600×600 mm,核心筒1~7层墙体厚度为500 mm,8~16层为450 mm,17~25层为400 mm,筒内墙厚度为250 mm,墙连梁为墙厚×1 200 mm,筒内梁为250×500 mm。
2.2 地震响应分析
本文共选取了三条实际地震波加速度记录作为激励,地震波具体信息如表1所示。由于结构在非线性状态下的力学机理复杂,而上文所述理论分析以及数值模拟方法无法充分保证相关结果的准确性,因此本文仅探讨结构在弹性状态下的力学性能及减震效果。在此对FCT结构、FDCT结构和FDRCT结构进行动力时程分析时,将三条地震波的加速度峰值统一调为0.07 g(多遇地震)。
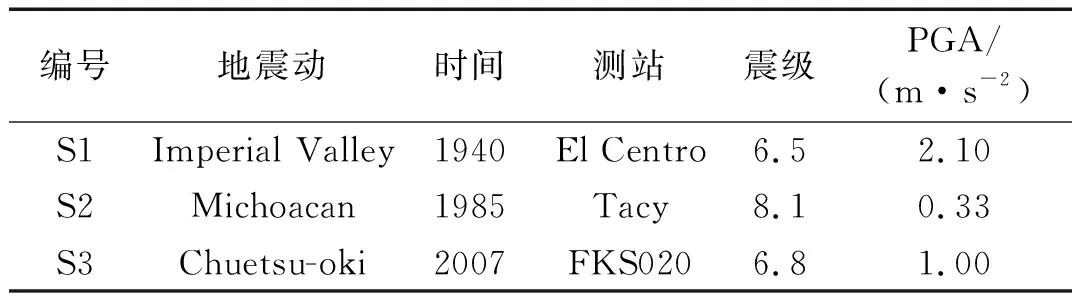
表1 地震动信息Tab.1 Information of ground motion
图6为三种结构在不同地震波下结构顶层的位移时程,从图中可以看出,相比于FCT结构,FDCT结构和FDRCT结构顶层位移会出现不同程度的增大。但相比于FDCT结构,FDRCT结构的位移有所减小,尤其是在峰值处的降幅更明显,可见将摇摆体系加入到本文所提出的新型分散筒结构中是有助于控制结构位移响应的。

(a) S1
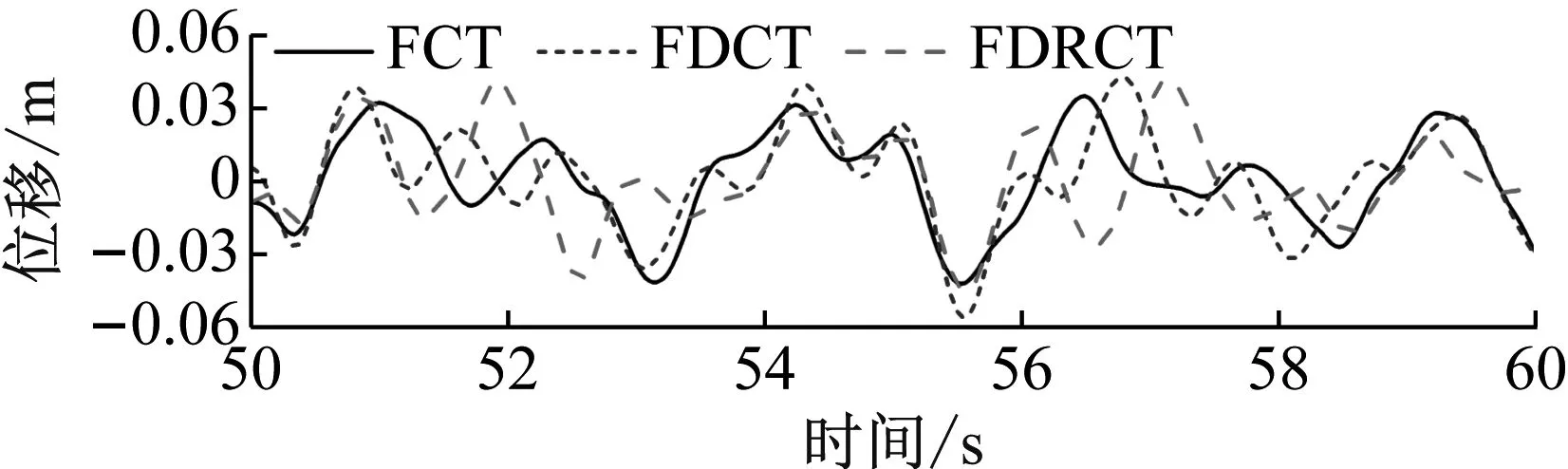
(b) S2
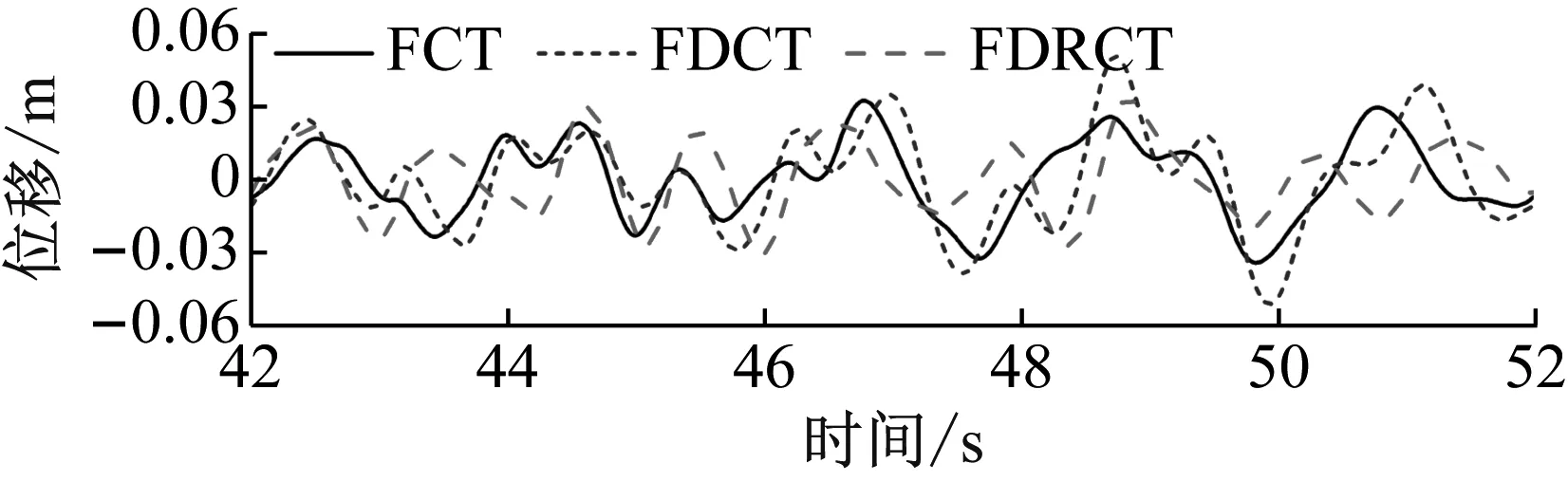
(c) S3图6 地震下结构顶层位移时程Fig.6 Displacement time history curves of top story of structure subjected to earthquakes
图7为三种结构在不同地震波下各层层间位移角对比,其中不同工况下结构的层间位移角均未超过规范要求的弹性状态下的限值1/800,证明三种结构在合理的设计下均具有足够的安全性能。可以看出:FDCT结构相对于FCT结构层间位移角呈现增大的情况,尤其是在结构中部楼层,层间位移角增大幅度更为明显,这是由于FDCT结构筒体围合面积的减小以及筒体进行了分散布置,结构刚度偏小,抗震能力偏弱,增加了薄弱层出现的几率。然而,FDCT结构层间位移角并未超限,且考虑此新型结构体系对结构经济性的提升作用,可认为该结构方案具备基本的可行性。FDRCT结构相对于FDCT结构展现出了明显的耗能减震优势,在三条地震波作用下其最大层间位移角分别减小了11.8%、27.1%和27.8%,且提高了结构变形的均匀程度。在S2波和S3波作用下,FDRCT结构大部分楼层层间位移角都接近FCT结构的结果,这表明相对于FDCT结构,FDRCT结构的动力响应显著降低,结构具备较强的抗震及耗能减震能力。

(a) S1

(b) S2

(c) S3图7 地震下结构层间位移角Fig.7 Inter-story drift ratio of structures subjected to earthquakes
为了直观评价三种结构各楼层层间变形的不均匀程度,并表征摇摆体系对结构变形和损伤的控制作用,可选用文献[18]定义的层间位移集中系数(drift concentration factor, DCF)来进行对比,量纲归一化指标DCF可按照下式计算,其数值越小表示结构楼层变形越均匀。
(12)
式中:αi为第i层的层间位移角;zi为第i层的层高;H为结构的总高度。
上述系数计算过程较复杂,宜提出一种机理明确且区分度更大的评价指标,参考统计学中变异系数的概念,本文认为可用结构各楼层的层间位移的变异系数(drift coefficient of variation, DCV)来评价不同结构各楼层层间变形的不均匀程度,其表达式如下,
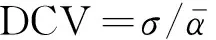
(13)
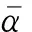
由式(12)和(13)计算得到的FCT结构、FDCT结构和FDRCT结构在不同地震波下的DCF和DCV如表2所示。从结果可知,相对于FCT结构,FDCT结构的数值都略有增大,而FDRCT结构的结果最小,这表明作为新增加的一道防线,分布摇摆芯筒能使结构变形更加均匀,有效控制结构的变形及损伤模式,最终提升了结构的抗震能力。对比三种结构的DCF和DCV,可以发现本文提出的DCV区分度更大,三种结构各楼层层间变形的不均匀程度可被明确区别,且DCV符合统计学原理,阈值合理且计算简便,在评价各楼层层间变形的不均匀程度方面更具备优势。

表2 不同结构DCF和DCV对比Tab.2 Comparison of different structural DCF and DCV
2.3 结构参数分析

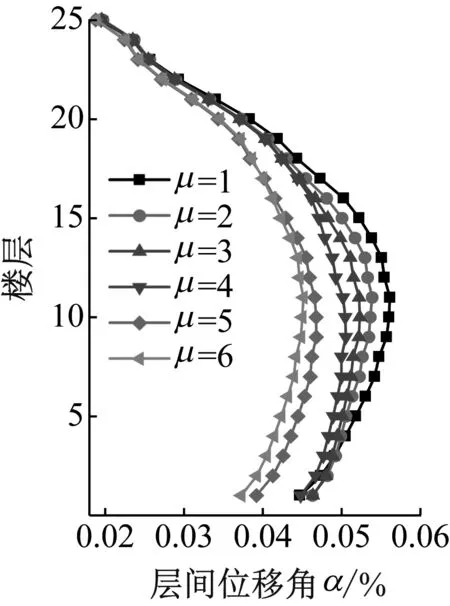
图8 不同μ对层间位移角的影响Fig.8 Effect of different μ on the inter-story drift ratio
值得指出的是,由于FCT结构、FDCT结构和FDRCT结构的有限元模型较为复杂,基于精细化有限元模型进行动力分析和大量参数分析的计算效率较低,且本文所建立的力学方程和数值模拟分析可以基本反映结构的动力特性和抗震能力,并为实际工程设计提供初步指导,因此不再进行有限元模型层面的对比分析。
3 地震动特性对结构耗能减震性能影响
相关研究表明,结构在不同场地条件下的动力反应特性具有一定差异性,有必要对此进行对比分析。由于本文所研究对象为高层结构,而高层结构属于长周期结构,在长周期地震动下此类结构的地震响应要远大于普通地震动下的情况[19]。此外,长周期地震动又包括近场长周期地震动(近断层脉冲型地震动) 和远场长周期地震动(远场谐和地震动),不同类型长周期地震动下高层结构的动力响应也会有差异[20]。有鉴于此,为了研究场地效应以及长周期地震动对FDRCT结构耗能减震性能的影响,本文参考文献[21-22]的选波原则,针对四类场地分别选取了5条地震波,同时选取了5条近场长周期地震波和5条远场长周期地震波,不同类型地震波加速度平均反应谱如图9所示。各种类型地震波统一按照加速度峰值为0.07g(多遇地震)进行调幅。
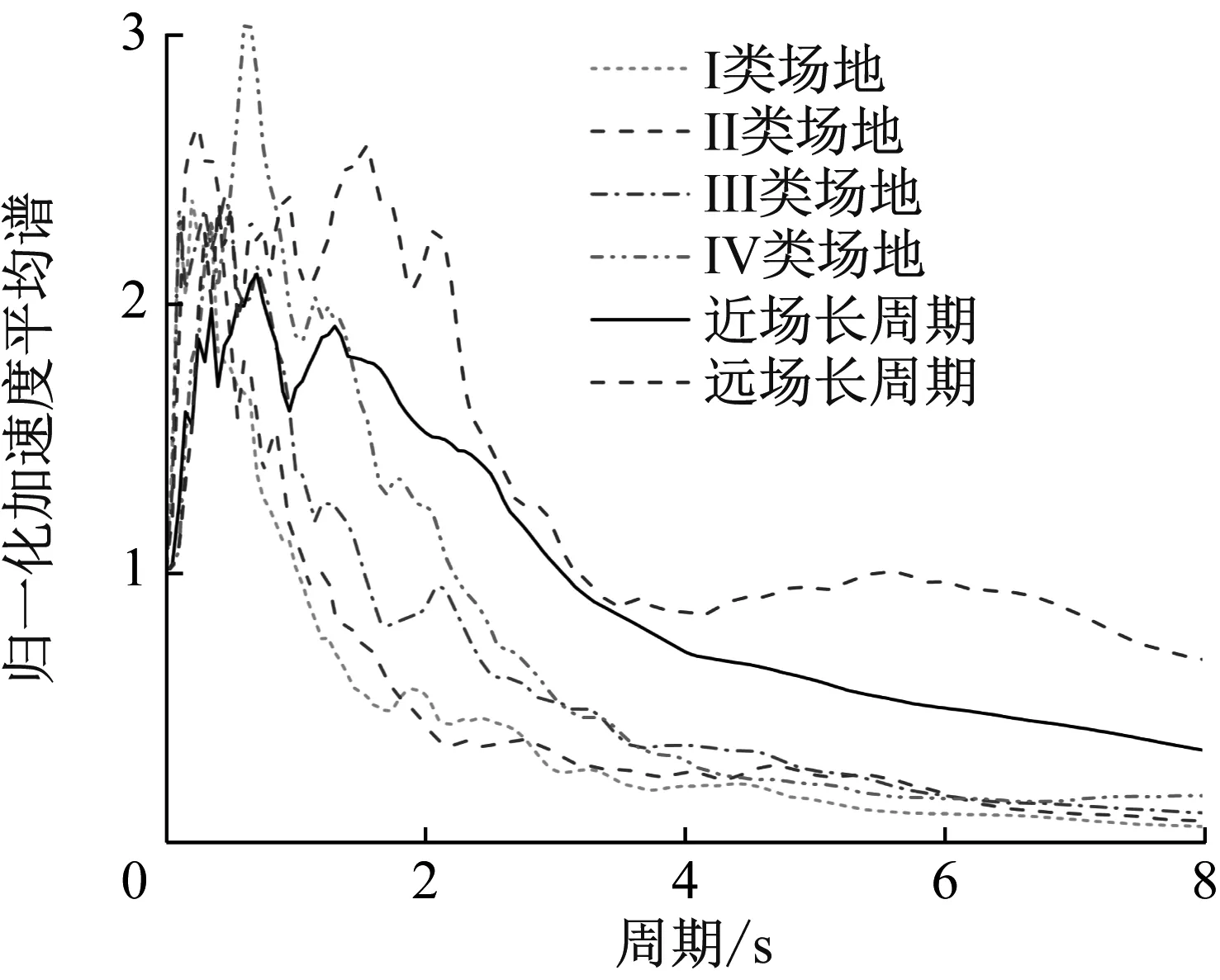
图9 地震波加速度平均反应谱Fig.9 Acceleration average spectrum of seismic waves
以上文分析中的FCT结构、FDCT结构和FDRCT结构模型为研究对象,对比分析不同类型地震波下三种结构的动力响应,探讨FDRCT结构的抗震及耗能减震性能。图10为FCT结构、FDCT结构和FDRCT结构在输入不同类型地震波下的层间位移角均值曲线。对比图10(a)~图10(d)可知,从Ⅰ类场地至Ⅳ类,三种结构的动力反应依次增大。四类场地中,FDRCT结构最大层间位移角相对于FDCT结构均有所减小,在Ⅳ类场地中降幅最大,且此情况下FDRCT结构与FCT结构的层间位移角曲线已较为接近,说明在软土地基中,具备摇摆功能的FDRCT结构拥有更优的耗能减震能力。

(a) Ⅰ类场地

(b) Ⅱ类场地

(c) Ⅲ类场地

(d) Ⅳ类场地

(e) 近场长周期
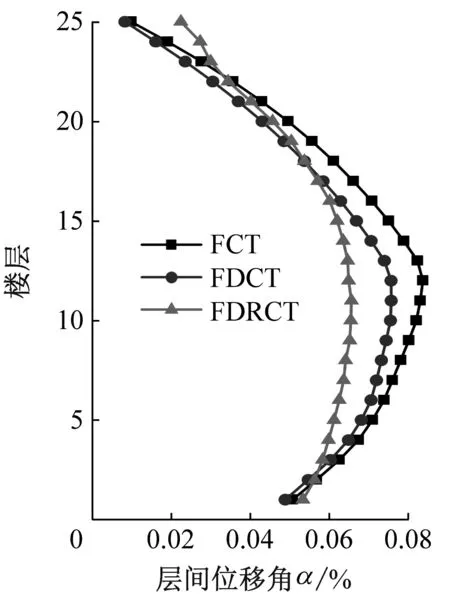
(f) 远场长周期图10 不同类型地震波下结构层间位移角对比Fig.10 Comparison of structural inter-story drift ratio under different types of seismic waves
由图10(e)和图10(f)可知,三种结构在长周期地震波下的动力响应显著高于普通地震动的结果,且相对于近场长周期地震波,远场长周期地震波对结构动力放大作用更为剧烈,这是主要是远场长周期地震波的谐振效应对结构响应进一步放大造成的。此外,FDCT结构和FDRCT结构的最大层间位移角均要小于FCT结构,这说明不具备摇摆能力的FDCT结构在长周期地震动下也呈现出良好的抗震能力。相对于FDCT结构,FDRCT结构的最大层间位移角在输入近场长周期地震波和远场长周期地震波时分别减小了17.0%和13.3%,这表明在长周期地震动下具备摇摆功能的FDRCT结构具备突出的耗能减震效果,更适合抵御近场长周期地震波所产生的脉冲效应。
此外,由图10中也可以看出:相比于FDCT结构,在不同类型地震波下,FDRCT结构的层间位移角曲线都呈现出了均匀的状态。为了更为直观的对比三种结构的不均匀程度,根据式(12)和式(13)分别计算出不同类型地震波下三种结构的DCF和DCV,结果如表3所示。

表3 不同地震波类型下结构的DCF和DCVTab.3 DCF and DCV under different types of seismic waves
从表3可看出,由于结构刚度的减小,FDCT结构相对于FCT结构其层间位移角不均匀性在不同类型地震波下会有不同程度增大,但在长周期地震波下,FCT结构和FDCT结构的DCF以及DCV十分接近,再次说明FDCT结构在抵御长周期地震波的可行性。三种结构中,FDRCT结构的DCF和DCV均为最小,层间变形最为均匀,再次证明附加摇摆体系的FDRCT结构能够有效控制结构的变形模式,降低结构的动力响应。对比不同类型地震波周期下FDRCT结构的DCF和DCV,Ⅰ类场地和Ⅱ类场地均匀程度要大于Ⅲ类场地、Ⅳ类场地和长周期地震波,这是软土场地和长周期地震波的频谱较为丰富,受高层摇摆结构的高阶振型的影响较大造成的,且本文提出的层间位移变异系数(DCV)更能凸显此种效应。
4 基于性能-利润总值的结构方案综合评估
FDCT结构和FDRCT结构的设计理念是为了提高结构的经济性。为了进一步分析附加摇摆功能的FDRCT结构的经济性与抗震减震能力的优势,参考抗震减震结构性价比评估的概念,本文提出了基于结构抗震性能与利润价格的评估指标,性能-利润总值S的计算公式如下
S=a∑γiPi+bC
(14)
式中:Pi为抗震性能指标,其为新型结构与原结构的抗震性能参数之比。本文将FCT结构作为原结构,将FDCT结构或FDRCT结构作为新型结构。本文根据结构特色选取最大层间位移角、DCF或DCV两种参数用以计算结构抗震性能指标。C为利润指标,其为原结构与新型结构利润值之比。a为抗震性能指标之和的权重系数,b为利润指标的权重系数,γi为各个抗震性能指标Pi对应的权重系数。其中,Pi和C均为越大越好,因此,S越大表明新型结构方案越优异。
为了对比DCF和本文所提出DCV作为结构性能-利润总值中的抗震性能指标所得结果的差异性,共设定了两种方案,第一种方案选取结构最大层间位移角以及DCF作为抗震性能指标,而第二种方案将DCF更换为DCV。本文追求的目标是提升结构经济性的同时保证结构的抗震性能,因此将式(13)中的权重系数a和b都设定为0.5,且本文对结构的抗震需求是在保证结构层间位移角尽可能减小的前提下再追求结构变形的均匀性,因此最大层间位移角所对应的P1的权重系数γ1设定为0.7,方案1中DCF和方案2中DCV所对应的P2的权重系数γ2设定为0.3。
本文研究的FCT结构、sFDCT结构和FDRCT结构三种模型的材料用量、成本和利润如表4所示。计算结构成本时,钢材单价取为5 000元/t,混凝土为500元/m3,梁铰为2 000元/个,分布摇摆芯筒基底铰支座100万元/组。计算结构收益时,可根据三种结构的筒体围合面积占比,计算得到FCT结构可出售的面积为30 000 m2,FDCT结构和FDRCT结构为32 800 m2,写字楼综合售价定为5万元/m2,收益与成本之差即为结构的利润。相比于FCT结构,FDCT结构和FDRCT结构利润值分别提升了9.27%和8.25%,显著提高了传统FCT结构的经济性。

表4 结构材料用量、成本和收益对比Tab.4 Comparison of structural materials consumption, costs and benefits
三种结构的性能-利润总值S结果如图11所示。两种方案计算所得的FDCT结构在不同类型地震波下的数值排序相同,而FDRCT结构的数值排序有所差别,这是由于方案2中的DCV更能突显Ⅰ类场地和Ⅱ类场地由于均匀程度较大而有效提升结构S的情况,比较不同结构的S时区分度更大,这也证明了本文提出的层间位移变异系数效果更优。在四类场地类别地震波下,相对于FCT结构,FDRCT结构的S都有不同程度的提高,而FDCT结构则都要小于FCT结构。在两种长周期地震波下,FDCT结构和FDRCT结构的S都要高于FCT结构,且在近场长近场地震波下提升最为显著,但整体对比分析而言,FDRCT结构的优势更为突出。由此可知,FDRCT结构具备兼顾经济性与安全性的优势,适宜在实际工程中推广使用。

(a) 方案1
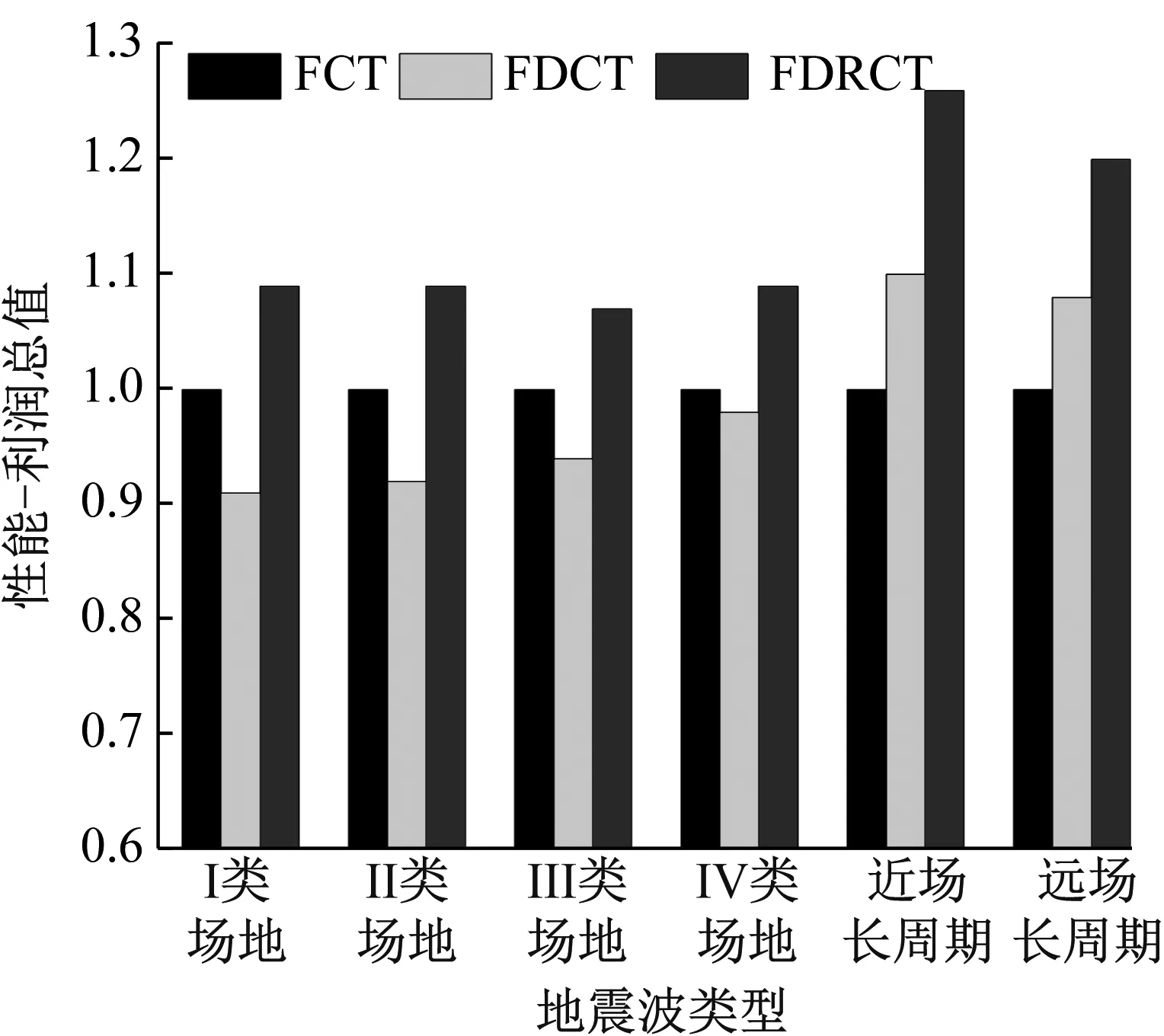
(b) 方案2图11 不同结构性能-利润总值S对比Fig.11 Comparison of different performance-profit values S
5 结 论
为了提升传统FCT结构的经济性,本文提出了附加分布芯筒的FDCT新型结构体系,进而将摇摆体系与分布芯筒结合提出了FDRCT结构体系,以改善结构由于刚度下降造成的抗震能力削弱。基于Lagrange方程建立了三种结构的简化动力模型,并进行了动力分析、场地效应和长周期地震波影响分析以及性能-利润总值评估,结论如下:
(1) 根据FCT结构、FDCT结构和FDRCT结构简化分析模型,基于Lagrange方程推导了相应的动力方程,并根据结构动力时程分析验证了该理论的可行性。地震作用下FDCT结构的动力响应相对较大,抗震能力有所下降。FDRCT结构顶层位移和最大层间位移角都要小于FDCT结构,对比三种结构的DCF和DCV结果,FDRCT结构的层间变形最为均匀,表明摇摆体系可以对本文中的分散筒结构有较好的控制效果,本文提出的DCV参数可以更准确便捷地评价楼层不均匀性。此外,由FDRCT结构地震作用下参数分析可知,增大分布摇摆芯筒的质量,可提高FDRCT结构的耗能减震能力。
(2) 对三种结构进行了不同场地类别以及不同类型长周期地震波下动力分析,结果表明远场谐和地震波对结构造成的累积破坏最为严重。在不同地震波类型下,FDRCT结构的动力响应结果都要小于FDCT结构,且DCF以及DCV皆为最小,证明了FDRCT结构因优越的耗能减震性能而具备广泛的适用性。相对于FCT结构,FDCT结构和FDRCT结构更有利于抵御长周期地震波的破坏,但FDRCT结构效果更为突出。
(3) FDCT结构和FDRCT结构相对于FCT结构的利润值分别提升了9.27%和8.25%。基于性能-利润总值的结构综合评估结果表明,FDRCT结构在不同类型地震波下其性能-利润总值都要优于FCT结构,尤其是在长周期地震波下提高幅度更大。FDRCT结构不仅可以提升结构的经济性,同时兼顾了结构的安全性,具备良好的推广应用价值。
