夯实基础,多管齐下
——谈立体几何中三类角的求解策略
2023-03-20安徽省芜湖市第十二中学夏旭东
■安徽省芜湖市第十二中学 夏旭东
立体几何问题综合考查同学们的空间想象、逻辑推理和数学运算等能力,其中“空间角”是高考每年必考内容,高考对“空间角”的考查,包括三类:线线角、线面角和面面角。空间直角坐标系的引入,使得空间向量坐标法以定量的计算代替了纯几何法的定性分析,以程序化的算法替代了繁难的推理论证。对于空间几何体本身不具备垂直关系,或图形本身不易建立空间直角坐标系,或虽能建系却不易求出点的坐标的立体几何问题,同学们往往束手无策,这一现象成为目前同学们学习立体几何亟待解决的问题。事实上,在很多有关立体几何空间角的问题中,综合几何法或基底法比通过建系使用向量坐标法求解更加便捷,解题效率更高。下面笔者通过几道例题与读者交流,以期抛砖引玉。
一、异面直线所成角的求法
1. 定义法(平移法)
解题策略:(1)平移:①利用图中已有的平行线平移;②利用特殊点(线段的端点或中点)作平行线平移;③补形平移。(2)证明:证明所作的角是异面直线所成的角或其补角。(3)寻找:在立体图形中,寻找或者作出含有此角的三角形,并解之。(4)取舍:所作的角为钝角时,应取它的补角作为异面直线所成的角。
例1如图1,P是平面ABC外一点,PA=4,BC=2,D,E分别为PC,AB的中点,且DE=3,则异面直线PA与BC所成角的大小为____。
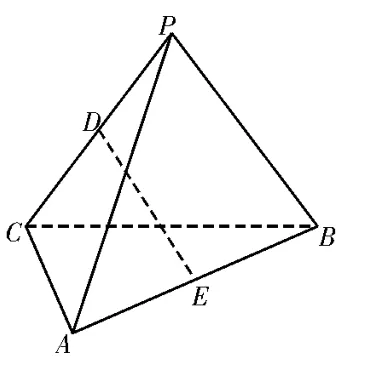
图1
解析:如图2,取AC的中点为F,连接DF,EF。在△PAC中,因为D是PC的中点,F是AC的中点,所以DF∥PA,同理可得EF∥BC,所以∠DFE为异面直线PA与BC所成的角(或其补角)。在△DEF中,DE=3,又DF==2,EF,则DE2=DF2+EF2,所以∠DFE=90°,即异面直线PA与BC所成的角为90°。
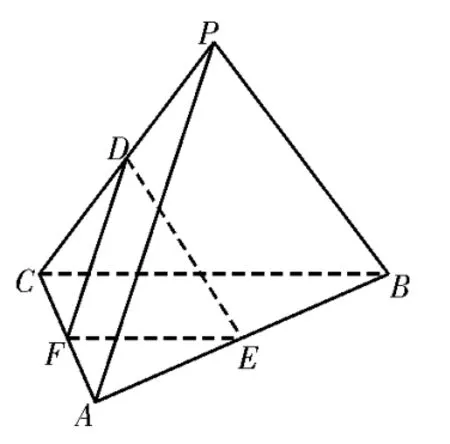
图2
例2在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小。
解法1:如图3,连接A1C1,B1D1,交点为O,取DD1的中点为G,连接OG,A1G,C1G,则OG∥B1D,EF∥A1C1,所以∠GOA1为异面直线DB1与EF所成的角(或其补角)。因为GA1=GC1,O为A1C1的中点,所以GO⊥A1C1,故异面直线DB1与EF所成的角为90°。
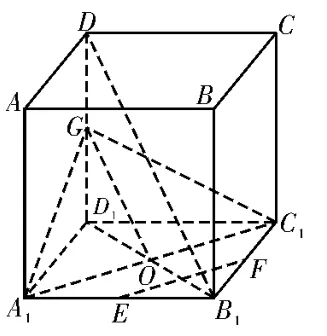
图3
解法2:如图4,连接A1D,取A1D的中点为H,连接HE,则HE∥DB1,HE=DB1,所以∠HEF为异面直线DB1与EF所成的角(或其补角)。连接HF,设AA1=k(k>0),则EF=,HE=,取A1D1的中点为I,连接HI,IF,则HI⊥IF,所以HF2=HI2+IF2=,所以HF2=EF2+HE2,所以∠HEF=90°,故异面直线DB1与EF所成的角为90°。
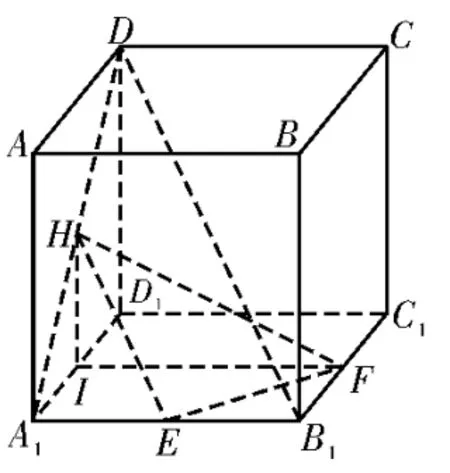
图4
解法3:如图5,连接A1C1,分别取AA1,CC1的中点M,N,连接MN。因为E,F分别是A1B1,B1C1的中点,所以EF∥A1C1。又MN∥A1C1,所以MN∥EF。连 接DM,B1N,MB1,DN,则B1N∥DM,B1N=DM,所以四边形DMB1N为平行四边形,所以MN与DB1必相交,设交点为P,则∠DPM为异面直线DB1与EF所成的角(或其补角)。设AA1=k(k>0),则MP=,DM=DP=,所 以DM2=DP2+MP2,则∠DPM=90°,故异面直线DB1与EF所成的角为90°。
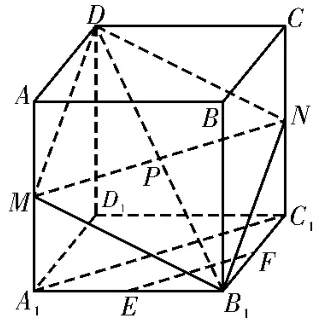
图5
2.向量法
若两异面直线的方向向量为a,b,则两异面直线所成角θ满足cosθ=
例3如图6,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别是PC,PB的中点。
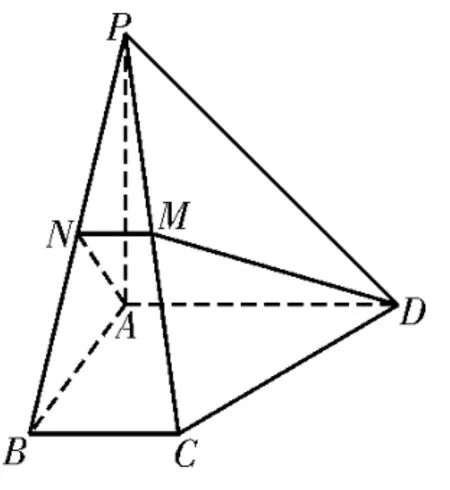
图6
(1)求证:PB⊥DM;
(2)求异面直线AC与PD所成角的余弦值。
解析:(1)证明过程略。
二、直线与平面所成角的求法
1.定义法
解题策略:(1)作:在斜线上选取恰当的点,过该点向平面引垂线,作出所求的角,其中确定垂足的位置是关键;(2)证:证明所作的角为直线与平面所成的角;(3)求:构造角所在的三角形,利用三角形的知识求角。
2.公式法
已知h为斜线上除垂足外的任一点到所给平面α的距离,l为该点到斜足的距离,θ为斜线与平面α所成的角,则sinθ=
3.向量法
已知AB为平面α的斜线,n为平面α的法向量,θ为斜线与平面α所成的角,则sinθ
例4如图7,已知多面体ABC-A1B1C1中,AA1,BB1,CC1均垂直于平面ABC,∠ABC=120°,AA1=4,CC1=1,AB=BC=BB1=2。
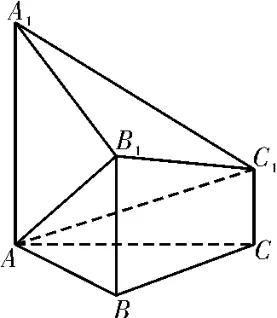
图7
(1)证 明:AB1⊥平 面A1B1C1;
(2)求直线AC1与平面ABB1所成角的正弦值。
解析:(1)证明过程略。
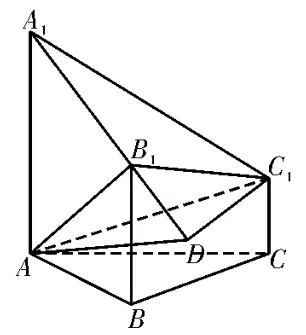
图8
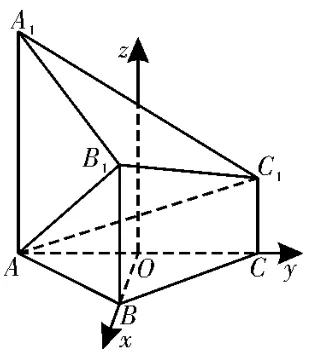
图9
三、二面角的求法
1.定义法
在二面角的公共棱上找一个特殊点,过该点在两个半平面内分别作垂直于棱的射线,这两条射线所夹的角为二面角的平面角。
2.垂面法
过棱上一点作棱的垂面,该平面与二面角的两个半平面的交线所形成的角即为二面角的平面角。
3.垂线法(三垂线定理法)
过二面角的一个半平面内一点作另一个半平面的垂线,过垂足向棱引垂线,利用三垂线定理找出所求二面角的平面角或其补角。
4.向量法
利用公式cos
例5如图10,在多面体ABC-A′B′C′中,AC=BC=且AC⊥BC,D为AB的中点,AA′⊥平面ABC,AA′∥BB′∥CC′且AA′=BB′=CC′=1。
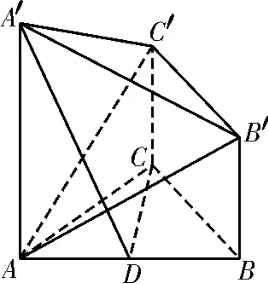
图10
(1)证 明:AB′⊥平 面A′DC;
(2)求平面AB′C′与平面ABC所成的锐二面角的余弦值。
解析:(1)证明过程略。
(2)方法1:如图11,因为BC∥B′C′,BC⊄平 面AB′C′,B′C′⊂平面AB′C′,所以BC∥平面AB′C′。因为BC⊂平面ABC,设平面AB′C′∩平面ABC=l,则l∥BC。因为BC⊥AC,所以BC⊥平面ACC′,所以l⊥平面ACC′,所以∠CAC′为平面AB′C′与平面ABC所成的锐二面角的平面角,因为cos∠CAC′=所以平面AB′C′与平面ABC所成的锐二面角的余弦值为
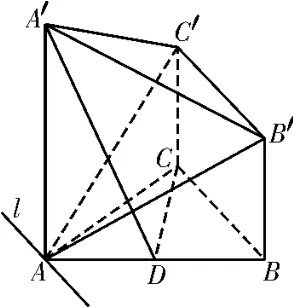
图11
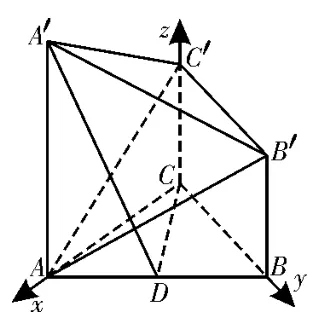
图12
