轮缘密封影响下的动叶通道内非定常流动研究

何振鹏，周佳星，辛佳，刘明远，黎柏春，张桂昌

(中国民航大学航空工程学院，天津 300300)

随着航空发动机性能的逐步提高，涡轮进口温度也不断增加，所需的冷却气体量也随之增加。大量的冷却气体经过轮缘密封间隙汇入主流降低了整个涡轮级的工作效率[1]，明确轮缘密封气流与主流道内气流相互作用机制对于提高涡轮级气动效率和优化涡轮结构设计有着重要意义。

国内外研究人员围绕封严气流与主流的相互作用开展了大量工作。国外方面，Zlatinov 等[2]通过数值模拟的方法研究了封严气流与主流的相互作用过程，将损失来源归结为封严气流与主流周向速度差引起的黏性剪切损失、封严气流对主流的堵塞作用及封严气流与动叶流场涡系的相互作用3 种。Schrewe 等[3]在两级低压涡轮实验台上通过实验测量将主流与封严气流相互作用所导致的涡轮级总压损失总结为4 种形式，即封严气体在上游形成堵塞，增大了主流通道内二次流损失，改变了转子上游流场，以及下游静叶流量导致额外的损失。Popovic 和Hodson[4-7]通过实验和数值模拟相结合的方法对轮缘密封下的主流和封严气流的非定常效应进行了研究，发现与定常计算相比由动叶转动引起的非定常特性减少了约10%主流损失，更为贴近实验结果；主流气动损失对于封严流量变化的敏感性受到上游静叶位势场和封严腔外部旋涡结构相互作用的影响；封严间隙的减小会提升轮缘密封的封严效率，同时也增加了主流流动损失对于封严流量的敏感性；轮缘密封与转子的相对轴向位置越近，封严气流负切向速度对于主流的影响越小，二次流损失越小。Monge-Concepcion 等[8]通过实验采用附加变量法研究了主流道气流、静叶尾迹在轮缘密封结构下的流动特征，结果表明，在静叶尾迹的影响下燃气入侵盘腔的流量近似成线性增加。Schreiner 等[9]研究了封严气流对于转子通道内端区二次流的影响，发现封严气流增加了盘腔内的流动不稳定性，封严气流出流加强转子通道内的二次流结构，其中马蹄涡压力面分支增强明显，马蹄涡吸力面分支受到削弱。国内方面，周杨等[10]通过数值模拟的方法研究了封严流量出现前后流场的分布，并分析了二次流在封严流量变化时的发展过程。贾惟[11-13]研究了轮缘封严出流对端区的影响及其非定常特性，发现封严出流对上游导叶的影响表现为对端区流动的堵塞作用，而在转子进口处则因为存在动量差相互剪切形成新的旋涡结构。吴康等[14-15]采用实验测量和数值模拟结合的方法研究了整级透平中入侵与封严变化机理，发现静叶尾缘的压力分布是造成燃气入侵的主要原因，复杂的封严结构能够避免主流和腔室内部气体的直接接触，增大主流入侵的沿程阻力和削弱主流的切向速度分量的影响。程舒娴等[16]通过数值模拟的方式研究了整周透平轮缘密封模型的流动与封严特性，发现盘腔内部封严效率存在周向波动但无明显周期性规律，静叶下游压力波动周期数等于静叶数，动叶上游与盘腔内部压力波动周期数等于动叶数。

以上关于涡轮端区轮缘密封封严气流与主流的相互作用的研究，分析了封严气流与主流相互作用机制及端区气动损失的具体形式。对于动叶通道内流动的非定常性及损失随时间的变化关注较少，没有把流动过程与气动损失统一起来。为了更加深入地了解受轮缘密封气流影响下动叶通道内的流动特性，本文采用1.5 级涡轮模型，在实验数据的支持下，以非定常数值模拟方法分析轮缘封严气流在动叶通道内与主流的交互作用。

1 研究对象和研究方法

1.1 研究对象

选取瑞士联邦理工学院叶轮机械实验室LISA 1.5 级涡轮为研究对象，详细的设计过程及气动参数参见文献[17]。图1 给出了本文使用模型的子午流道图，封严腔结构及与涡轮主流通道相对位置如图所示。

图1 带有前后腔的1.5级涡轮子午面Fig.1 Meridian channel of 1.5-stage turbine with front and aft seal cavity

数值模拟采用ANSYS CFX 18.0，求解三维URANS 方程，湍流模型采用SST。空间离散采用二阶迎风格式，时间离散采用二阶后差欧拉格式，工质为理想气体。为节省计算资源并满足转静交界面模型要求，涡轮叶片数由36∶54∶36 约化为2∶3∶2，为保证与实验数据的一致性，本文不改变整体叶型结构。涡轮主流通道和轮缘密封结构网格均由AutoGrid5 生成。为了减小插值计算所带来的误差，封严腔体与涡轮主流通道交界面处采用了轴向和周向节点完全匹配的网格，并在壁面附近加密，如图2 所示。壁面第1 层网格距离为1µm，保证y+≈1满足湍流模型的要求。计算网格总数约为937 万，其中，静子网格数约为195 万，转子网格数约为400 万，封严腔体网格数约为110 万。

图2 1.5级涡轮计算网格Fig.2 Computation mesh of 1.5-stage turbine

1.2 边界条件

数值模拟中，主流进口为压力进口边界条件，给定总温328.15K 和总压1 4 0 kPa，进气方式为轴向进气。出口为压力出口边界条件，给定静压。动叶转速为2700 r/m in，固体壁面为光滑、绝热、无滑移壁面。封严腔体进口为流量进口边界条件，给定总温323.15 K 和封严流量。封严流量以封严流量占主流流量之比(IR)的形式给出，所选用封严流量比IR 分别为0，0.5%，0.9%，1.3%和1.7%，IR=0 表示封严腔存在不施加封严流量的工况，Endwall 表示无封严腔体工况。详细的边界条件见文献[18]。转静交界面设置在封严腔出口下游，靠静叶侧封严腔壁面设置为静止壁面，靠动叶侧封严腔壁面设置为转动壁面。定常计算转静交界面采用Frozen Rotor模型，非定常计算采用Transient Rotor Stator 模型。定常计算完成后，结果作为非定常计算初场。时间步长设置为1.03×10−5s，即动叶经过2 个静叶通道的一个周期时间设为120 个物理时间步，每一个物理时间步内迭代步数为10，残差设置为10−6。当监测点关键参数呈现出随时间周期性变化保持2 个周期以上时认为计算收敛。

图3 为IR=1.3%时非定常计算中动叶监测点静压的变化。可知，当计算到800 个时间步左右时，静压出现明显的周期性变化，非定常计算收敛。

图3 监测点静压变化Fig.3 Static pressure changes at monitoring points

1.3 计算验证

图4 给出了无封严腔体(Endwall)时，动叶出口周向质量平均相对流动角沿径向分布的定常和非定常时均结果与实验测量结果[17]对比。定常与非定常计算结果基本一致，与实验测量结果相比，由于LISA 1.5 级涡轮实验台在动叶与第2 列静叶间存在轮缘间隙，实验中部分主流气体入侵后封严腔，影响了叶根位置气流偏转角。另外，实验中为防止传感器探针与转子发生碰磨，探针无法贴近叶根低半径位置，无法获得准确的实验数据；同时，轮毂低半径位置贴近转静间隙，误差受实验件加工与装配精度的影响也较为显著。鉴于以上原因，在进行数值模拟仿真时，当所得测量值与实验值相差小于5%时，认为结果数值结果与实验测量的相对误差在可接受的范围。

图4 动叶出口周向质量平均相对流动角Fig.4 circumferential mass-averaged relative flow angle at rotor exit

图5 给出了设计工况下（IR=0.9%）转子出口相对总压系数云图实验[18]和非定常时均结果的对比。相对总压系数Cpt定义如下：

图5 IR=0.9%时相对总压系数云图Fig.5 Contour of relative total pressure coefficient when IR=0.9%

式中：Pt,rel为相对总压；Pinletl为入口位置总压。

由图5 对比可知，在转子出口存在轮毂二次流、叶尖通道涡及叶尖泄漏涡3 个低压区，其相应位置和形状都较为相似。数值模拟与实验测量的轮毂二次流相对总压系数最大不超过5%，认为数值结果与实验测量的相对误差在可接受的范围。

综合图4 和图5 数值模拟和实验测量的结果对比，可以认为本文所采用的数值方法能够准确模拟带有轮缘密封的1.5 级涡轮内部流场的流动结构。

2 结果分析

2.1 动叶入口

图6 给出了IR=0.5%和IR=0.9%封严腔出口径向速度与总压云图。图中：Tr表示整周周期的1/54，即动叶通过一个转子通道的时间，Tavg表示Tr时间内的平均结果。径向速度为负，代表燃气入侵；径向速度为正，代表封严出流。观察图6(a)、(b)中时均径向速度分布，IR=0.5%时，燃气入侵位置集中于静叶尾迹下游，封严出流位置集中于静叶吸力面下游，2 处位置分布于静叶尾迹两侧，表明前封严腔出口处流场受到上游静叶尾迹影响较大。封严流量增加至IR=0.9%，封严出流和燃气入侵强弱较IR=0.5%明显不同，此时封严气流基本阻隔了燃气对于盘腔的入侵，封严出流明显。

图6 封严腔出口径向速度与总压云图Fig.6 Contours of radial velocity and total pressure at seal cavity exit

在各时刻径向速度云图中，用2 条线分别标示了燃气入侵和封严出流位置。总的来看，静叶与动叶相对位置的变化整体上并未使得燃气入侵和封严出流位置在Tr周期内发生大的周向偏移，仅出现一定程度的相位滞后。封严腔出口气流的径向速度随燃气入侵与封严出流的变化在Tr周期内发生剧烈波动。以图中编号为2 的动叶运动为切入点，Tr时刻，2 号动叶前缘接近静叶尾迹区域，动叶势场和静叶尾迹的相互作用造成该位置压力波动，由图6 中实线可以看出随着时间变化燃气入侵逐渐增强。同时，由于受到2 号动叶压力面侧高压区域的影响，静叶吸力面下游压力升高，图中虚线标示的封严出流较弱。和时刻，2 号动叶旋转运动逐渐远离静叶，在静叶尾迹的作用下，封严腔出口燃气入侵范围扩大且强度增强。2 号动叶压力面侧高压区域远离静叶吸力面，以及1 号动叶吸力面的靠近，使得静叶吸力面下游压力恢复至原先的低压，由图6 中虚线可以看出，随着时间变化封严出流逐渐减弱。Tr时刻，2 号动叶前缘与上游静叶相对距离较远，对于封严腔出口气流影响较小。1 号动叶接近静叶尾缘，受其势场及压力面侧高压影响，封严腔出口燃气入侵和封严出流位置周向偏移且范围缩小。在下一个Tr周期时刻，1、2 号动叶将出现在此周期时刻2、3 号动叶的位置并与该静叶重复上述过程。可以看出，静叶与动叶相对位置的变化所导致封严腔出口气流变化仍与动叶的运动周期一致，封严出流与燃气入侵随时间的变化与主流通道内的压力随时间变化相关。

为了观察动叶入口位置非定常效应随封严流量的变化情况，使用均方差值来量化非定常行为[19]。图7 给出了动叶进口相对总压Tr周期内均方差分布。图中用10%～50%标注出了相应的叶高，下文标示方法与此相同。无封严结构（Endwall）时，由于受到动叶前缘势场影响，轮毂10%叶高位置存在总压高波动区域。IR=0 时，此时存在封严结构，但无封严气流，轮毂附近的部分气体入侵盘腔，在10%叶高以下径向范围内形成了又一总压波动区域。同时，通道内气体的损失使得无封严结构时压力波动区域范围缩小。IR=1.3%时，封严气体出流与主流的掺混使得轮毂附近压力波动增强，高波动径向位置降低至5%叶高，表明动叶入口位置非定常波动主要受动叶前缘势场影响转变为受轮缘封严气流与动叶前缘势场共同作用。10%叶高以上区域由于受到封严流的堵塞，主流道内径向压力梯度增加，沿半径气流分布改变，相对总压波动稍有减小。

图7 动叶进口相对总压Tr周期内均方差分布Fig.7 Relative total pressure RMS in Tr cycle at rotor inlet

图8 和图9 给出了动叶进口时均径向速度及均方差径向分布。IR=0 无封严气流时，径向速度相较于无封严结构时有所增加，且在约5%叶高位置出现极值。这意味着主流道气流侵入盘腔后随盘腔旋转再次进入了主流道，使得主流径向动量在掺混后增加，5%叶高位置封严出流所形成的堵塞效应最为强烈。封严流出现后，动叶入口全叶高位置气流径向动量大幅增加，5%叶高处的速度极值增加最为显著。观察图9 可以发现，在封严结构与封严气流在10%叶高以下区域形成最为强烈的径向速度波动。对比图8，在径向速度极值出现的相同叶高位置径向速度波动最为强烈，意味着封严出流堵塞作用强烈的位置非定常效应也最为明显。

图8 动叶进口时均径向速度径向分布Fig.8 Radial distribution of time-averaged radial velocity at rotor inlet

图9 动叶进口时均径向速度均方差径向分布Fig.9 Radial distribution of time-averaged radial velocity RMS at rotor inlet

图10 给出了时均结果下动叶入口周向质量平均相对流动角。图中曲线从右至左封严流量依次减小，IR=0 无封严气流时，主流道近壁面气流侵入盘腔减小了3%叶高以下气流方向对轴向的偏转。IR=0.5%时，10%叶高以下气流方向偏转角减小。IR=0.9%，IR=1.3%和IR=1.7%时，轮毂附近气流出现相反方向的偏转，此时轮毂端区气流在受到动叶前缘势场与压力面侧高压区域作用后偏转至动叶吸力面。

图10 动叶入口周向质量平均相对流动角Fig.10 Radial distribution of circumferential mass-averaged relative flow angle at rotor inlet

2.2 动叶通道

图11 给出了时均结果下动叶轮毂位置相对总压云图。观察图11(a)、(b)可以发现，IR=0 封严结构的存在虽然使得主流道近端壁附面层流体部分损失，但在动叶前缘势场作用下形成马蹄涡的区域压力变化并不明显，如图11 中区域A 所示。IR=0.9%和IR=1.7%时，结合图10 分析可知，动叶入口轮毂位置气流方向受封严气流影响发生偏转，动叶前缘马蹄涡滞止点位置也随之向吸力面侧的移动。还可以观察到，动叶通道内压力面侧高压区范围扩张，吸力面相对低压区轴向后移的同时向相邻动叶压力面侧移动，呈现出偏离吸力面的态势。吸力面侧扩压区位置轴向后移，整体范围收缩绝对值增加，如图11 中区域B 所示。

图11 动叶轮毂位置相对总压云图Fig.11 Relative total pressure contours at rotor hub

图12 给出了不同封严流量时均结果下的动叶通道端区三维流线分布。相较于无封严结构，IR=0 时轮毂近壁面气体部分入侵盘腔对于动叶前缘流场影响并不明显。IR=0.9%时，低速流体大量增加，马蹄涡滞止点位置变化，压力面分支明显增强，在与相邻动叶马蹄涡吸力面分支汇合后更加贴近吸力面壁面。IR=1.3%时，封严流量进一步增加上述变化更加明显。结合图10 分析可知，封严流量的加入使得动叶轮毂端区气流量增加，马蹄涡滞止点位置向动叶吸力面侧移动也造成更多的气流汇入马蹄涡压力面分支，马蹄涡压力面分支增强，通道内横向压力梯度增加，动叶前缘压力面高压区域扩张，吸力面相对低压区减弱。

图12 动叶通道端区三维流线分布Fig.12 3D streamline at rotor passage endwall

图13 给出了不同封严流量下动叶前缘三维旋涡结构示意图，涡结构使用Q 准则识别，取Q=8.15×107等值面并用轴向涡量进行着色。无封严结构时，动叶前缘存在马蹄涡压力面分支(horse vortex pressure s i de l eg,HV-PSL)与吸力面分支(ho r se vortex suction sideleg,HV-SSL)。IR=0.5%时封严气流出现，少量封严气流出气流与主流发生掺混，图13(b)可以观察到，因封严出流气体与主流存在周向动量差剪切作用，在吸力面侧形成剪切诱导涡结构(shear induced vortex,SIV)，其在向后的发展过程中与马蹄涡压力面分支和吸力面分支交汇形成轮毂通道涡(passage vortex,PV)。IR=0.9%时，封严流量进一步增加，剪切诱导涡结构增强。结合图11 可知，封严气流影响形成的剪切诱导涡及其在动叶通道内的发展在轮毂位置表现为相对低压区位置向动叶通道中间移动。

图13 动叶前缘三维旋涡结构示意图Fig.13 Schematic diagram of 3D vortex structure at the leading edge of blade

图14 给出了时均结果下45%、60%和80%动叶通道轴向涡量云图。相较于无封严结构，IR=0.9%时，45%动叶通道轴向位置处靠近吸力面侧轮毂通道涡结构已经出现，由图13 分析可知，这是由于封严出流形成的剪切诱导涡参与了通道涡的形成过程，同时横向压力梯度的增强使得通道内气流更加贴近吸力面，该轴向位置低半径处通道涡结构提前出现。60%动叶通道轴向位置处，IR=0.9%通道涡结构范围扩张，涡核径向位置更高。在80%动叶通道轴向位置处，IR=0.9%通道涡范围的扩张使得壁面涡在形成的过程中径向位置也随之提高。对比图11，可以判断通道涡形成过程的变化与涡量结构的增强导致了吸力面侧扩压区的变化。

图14 动叶通道轴向涡量云图Fig.14 Axial vorticity contours of blade passage

图15 给出了动叶10%叶高位置Tr周期内各时刻熵增云图，用虚线标示了Tr周期内动叶位置的变化。熵增的定义如下：

式中：Tt,in和Pt,in分别为主流进口总温和总压；cp为定比压热容；Rg为气体常数；Ts和Ps分别为当地静温和静压。

对比图15(a)、(b)中有无封严气流时均结果可知，封严气流在动叶通道内产生了又一高熵增区域，为了明确其产生与在动叶通道内的发展变化，选取各时刻内的熵增变化进行详细分析。

图15 动叶10%叶高位置Tr周期内各时刻熵增云图Fig.15 Contour of entropy increase at every moment of Tr cycle at 10% blade height position

无封严流量时，因静叶与动叶数目比为2∶3，相邻动叶通道内熵增变化并不相同。动叶前缘靠近静叶尾迹因其前缘势场的存在引起尾迹周向变形压缩，而后动叶继续旋转前缘将尾迹向吸力面与压力面分开为2 支，吸力面一支轴向运动向后汇入通道涡，压力面一支持续有尾迹汇入直至受到下一动叶吸力面挤压而被动叶前缘分开。IR=1.3%时，静叶尾迹形成过程中受到封严出流堵塞作用而减弱，但在随后的发展过程中有了封严气流的汇入而增强。当有封严气流汇入的尾迹流受到动叶前缘的挤压与分割时，吸力面侧尾迹熵增区域更大。除尾迹流形成的熵增区域外，动叶通道内吸力面侧出现随时间轴向运动的高熵增区域。对比IR=0 与IR=1.3%在10%叶高位置时均熵增分布可以发现由封严气流所造成的吸力面侧高熵增区域。由图13、图14分析可知，封严气流作用下轮毂通道涡的形成过程与无封严气流时不同，吸力面侧高熵增区域即为剪切诱导涡出现后参与通道涡的形成过程所导致。

综上可知，封严气流一方面增强了原静叶尾迹在动叶前缘的损失，另一方面以剪切诱导涡的形式参与通道涡结构的形成过程造成额外的损失。

图16 给出了时均结果下动叶吸力面剪切应力云图与极限流线图。相较于无封严结构时，IR=0、IR=0.9%、IR=1.7%封严气流的出现对于主流道形成堵塞作用使得径向压力梯度增加，动叶轮毂位置前缘至30%轴向弦长位置端壁极限流线变化。结合图11、图12 可知，封严气流的出现使得动叶通道内压力面向相邻动叶吸力面横向压力梯度增加，轮毂端区气流向吸力面侧集聚。结合图13、图14 分析可知，轮毂附面层流体的增加与剪切诱导涡参与通道涡形成，使得轮毂二次流在动叶通道内径向位置较无封严结构时更高。在以上因素的共同作用下，吸力面壁面极限流线折转角度增加，壁面高摩擦力区域扩大，叶片载荷增加。

图16 动叶吸力面剪切应力与极限流线图Fig.16 Contours of wall shear stress and limited streamlines near rotor suction side

图17 给出了动叶5%叶高和40%叶高处叶片表面静压系数Cps非定常时均值分布。选取无封严时的非定常结果作对比。图中横坐标用动叶轴向弦长无量纲化，纵坐标为无量纲静压系数，该系数Cps_R可表示为

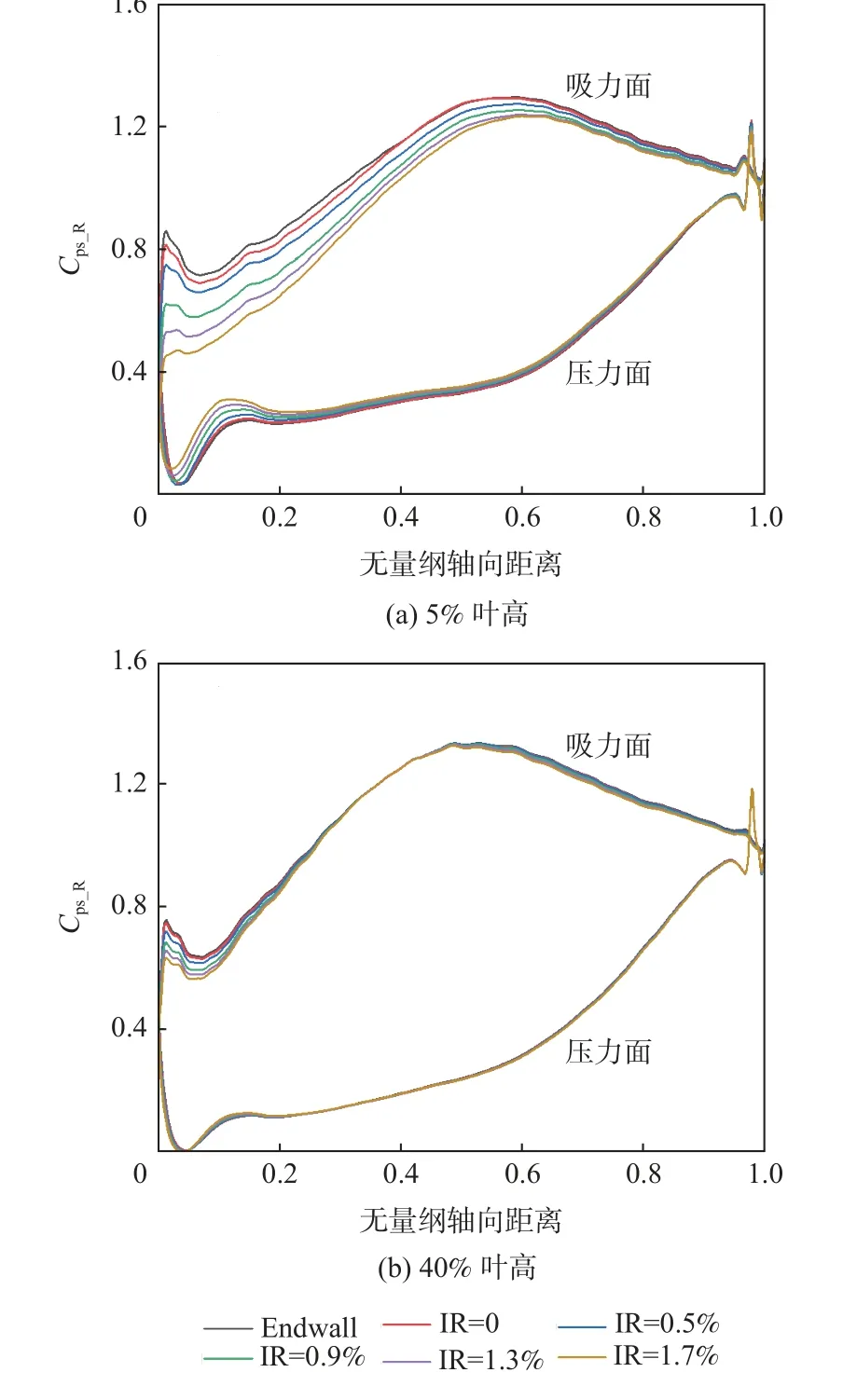
图17 动叶表面静压系数分布Fig.17 Static pressure coefficient distribution on blade surface

式中：Pt为动叶通道进口总压；P为叶片表面当地静压；Pr为动叶通道出口静压。总的来看，封严气流的出现增加了动叶吸力面负荷，降低了动叶压力面负荷，对动叶吸力面影响明显要大于动叶压力面。

5%叶高位置处，动叶整个吸力面几乎都受到了封严流量造成的加载，自动叶前缘开始沿吸力面载荷逐渐趋于一致。结合图13、图14 分析可知，封严气流改变了马蹄涡滞止点且通道内气流向吸力面侧集聚，使得动叶前缘与吸力面侧负荷增加，压力面负荷降低。吸力面1%动叶弦长位置出现最大载荷，与无封严腔时相比，IR=0.5%、IR=0.9%、IR=1.3%、IR=1.7%最大静压系数分别降低了0.11、0.23、0.33、0.404。动叶压力面从0 至80%轴向弦长静压系数都有所升高，最大位置出现于10%动叶轴向弦长处。

40%叶高位置处，动叶吸力面受影响区域分为2 个部分，分别为0～30%轴向弦长和50%～90%轴向弦长，幅度变化明显低于5%叶高位置，该径向位置主要受到封严流径向动量堵塞作用影响。0～30%轴向弦长封严流量造成的加载较大，同5%叶高位置变化类似，自动叶前缘开始沿吸力面逐渐减弱。与无封严结构时相比，IR=0.5%、IR=0.9%、IR=1.3%、IR=1.7%最大静压系数分别降低了0.023、0.046、0.062、0.129。50%～90%轴向弦长虽然也出现了静压系数的波动，但变化微弱。40%叶高位置动叶压力面受封严气流影响不大，不同封严流量下静压系数曲线基本重合。

2.3 动叶出口

图18 给出了时均结果下动叶出口熵增云图。相较于无封严结构，IR=0 无封严气流时出口位置熵增变化并不明显。IR=0.9%和IR=1.3%时，封严气流增加了轮毂附面层，同时改变了通道涡的形成机制，使得动叶出口位置二次流结构径向位置抬升损失加剧。

图18 动叶出口熵增云图Fig.18 Entropy increase contours at rotor outlet

为了量化封严气流在动叶通道出口损失情况，图19 给出了Endwall、IR=0.5%、IR=0.9%、IR=1.3%、IR=1.7%动叶出口时均周向质量平均熵增径向分布。对比无封严结构，IR=0 封严结构出现加剧了熵增损失。封严气流出现后，主流熵增损失径向位置扩展至60%叶高。3%～5%叶高熵增极小值对应动叶出口角涡径向位置，熵增减小表明其受封严气流影响减弱。10%～40%叶高，熵增极大值随封严流量增加不断增加的同时径向位置升高，对应于动叶出口通道涡与尾缘脱落涡，变化趋势与图18 一致。动叶出口位置二次流损失相较于无封严结构时，IR=0、IR=0.5%、IR=0.9%、IR=1.3%、IR=1.7%分别增加了6.78%、21.29%、28.11%、36.8%、42.92%。

图19 动叶出口周向质量平均熵增径向分布Fig.19 Radial distribution of entropy increase at the blade outlet

3 结 论

采用三维URANS 方法和SST 模型，分析了轮缘封严气流对于高压涡轮转子通道内流场的影响及所产生的损失，得出如下结论：

1）封严腔出口气流受静叶与动叶相对位置变化的影响呈现较强的非定常特性，变化周期仍与动叶的运动周期保持一致。燃气入侵与封严出流现象的出现与主流通道内的压力随时间变化一致。

2）封严气流出现后，动叶入口位置非定常波动由主要受动叶前缘势场影响转变为受轮缘封严气流与前缘势场共同作用。封严气流减小了动叶入口的周向速度，轮毂端区气流出现反方向偏转，在受到动叶前缘势场与压力面侧高压区域作用时偏转至动叶吸力面。封严气流增大了动叶入口处径向速度的同时也在封严出流堵塞作用最强的位置造成了强烈的非定常效应。

3）封严气流改变了动叶前缘马蹄涡滞止点位置，增强了马蹄涡压力面分支。封严气流与主流在动叶通道内掺混形成剪切诱导涡改变了原通道涡的形成机制和吸力面侧相对低压区的位置。

4）封严气流一方面增强了原静叶尾迹在动叶前缘的损失，另一方面以剪切诱导涡的形式参与通道涡形成过程造成额外损失。封严气流增加了动叶吸力面负荷，降低了动叶压力面负荷，对动叶吸力面影响明显要大于动叶压力面。动叶出口轮毂二次流结构受封严气流影响径向位置抬升且损失增加。