定比点差法在圆锥曲线中的应用

李小蛟

(四川省成都市树德中学 610091)

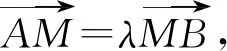
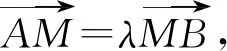
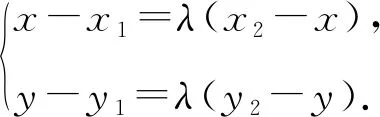
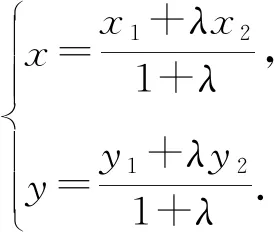
下面我们通过近年高考试题和模拟试题的解答，从不同题型剖析定比点差法在圆锥曲线问题中的实际应用.

1 定值问题

(1)求椭圆的方程；

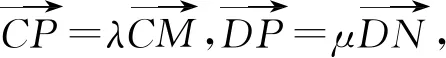
(3)设点P(x0,y0),M(x1,y1),N(x2,y2)，

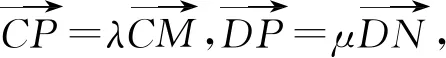
(x0+4,y0)=λ(x1+4,y1),

(x0-4,y0)=μ(x2-4,y2).

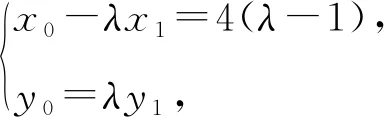
所以λx1-ux2=8-4(λ+μ).

①

又点P,M,N均在椭圆上，

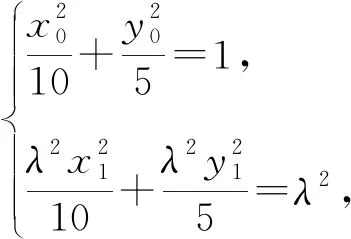
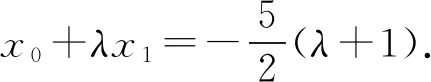
②

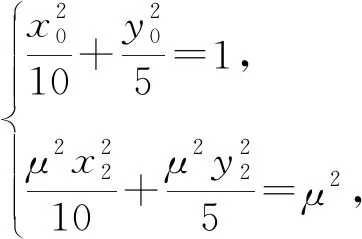
③

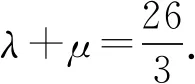
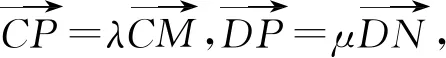
2 定点问题

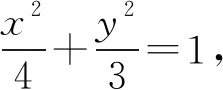
解析由对称性可知，直线AC过定点必在x轴上，不妨设M(m,0),A(x1,y1),B(x2,y2)，则C(x2,-y2).

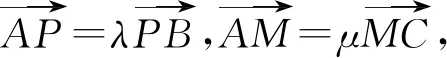
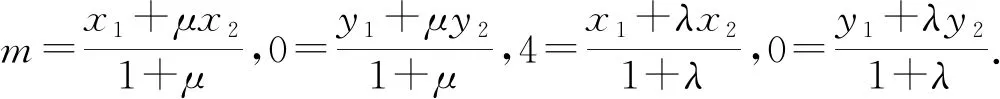
则λ=-μ.

又A,B两点在椭圆上，

两式相减可得

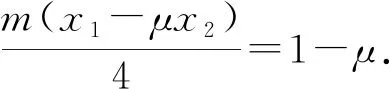
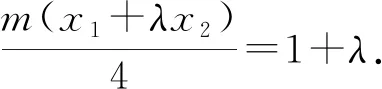
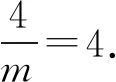
所以m=1.

即直线AC过定点(1,0).

评注本题考虑到A,B,P三点共线和A,C,M三点共线，故将点P转化为点A,B定比分点，将点M转化为点A,C定比分点，从而利用定比分点公式找到坐标之间关系；利用定比点差法将相关量之间进行转换，减少运算量，观察等式结构很容易找到所求参数m的值.

3 定直线问题

(1)求椭圆的方程；

(2)设点Q(x,y),A(x1,y1),B(x2,y2)，

又A,P,B,Q四点共线，从而

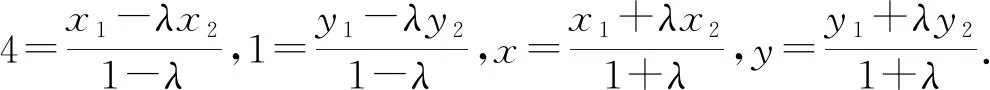
④

⑤

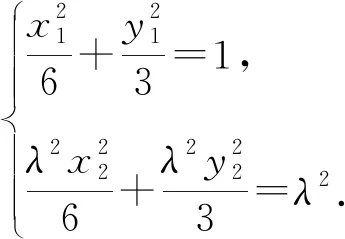
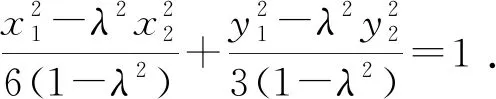
即点Q总在直线2x+y-3=0上.

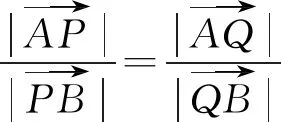
4 最值问题

⑥

⑦

将⑦代入⑥可得y1-2y2=-m.

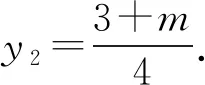
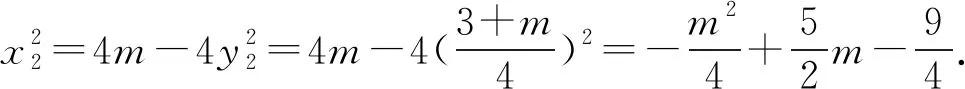
5 范围问题

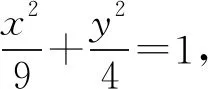
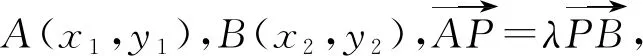
所以x1+λx2=0,y1+λy2=3+3λ.

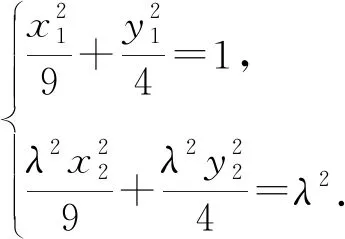
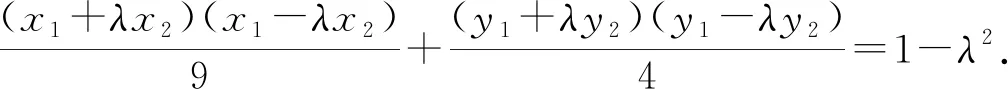
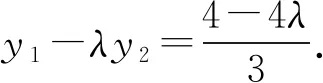
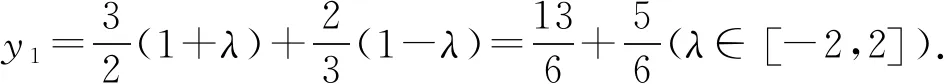
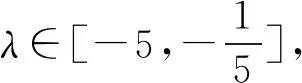
评注本题的解答中，范围求解要依赖于椭圆中相关量的范围解答，定比点差法的处理使所求解参数λ很快与相关点A,B的坐标之间建立等量关系，从而关系交代清晰明了，简化运算，事半功倍.

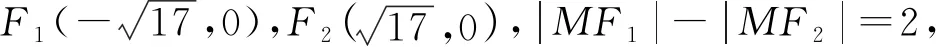
(1)求C的方程；

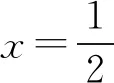
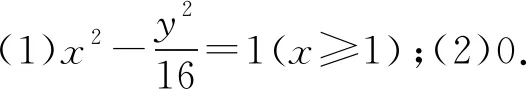
(1)求椭圆C的标准方程；

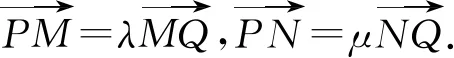
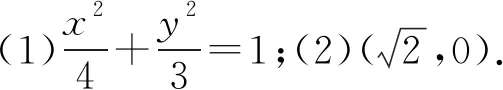
变式练习3(2021年全国高考乙卷数学(文)试题)已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2．

(1)求C的方程;

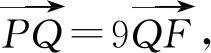
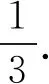
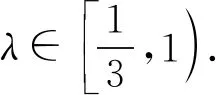
定比点差法是圆锥曲线中对线段比例关系处理的一种技巧，在题目中遇到三点共线、定点、成比例等条件时，我们可以充分地考虑这一思路，以起到事半功倍的效果.