殊途难归到殊途同归

江苏省启东折桂中学(226200) 陈建超

江苏省启东市大江中学(226215) 李卫星

反比例函数的定义中,形如y=(k≠0)的函数则称y是x的反比例函数.定义中的解析式则显露出了一切,k是图像任意一点横纵坐标的乘积,这是代数意义;而|k|是此点与坐标轴所构成的面积,这是几何意义.数有数的好处,形有形的妙处,如若能挖掘其中数与形的关系并恰当地利用,则能为后续教育教学提供简洁有力的技巧和方法.

1 不期而遇

案例1如图1,∆OAC的顶点A在双曲线y=上,点C在x轴上,直线AC与双曲线y=只有唯一公共点,且AC与y轴不平行,则S∆OAC=____.

图1

此题是以反比例函数为背景求解面积的问题.求解三角形的面积无非利用底乘高或者进行面积比例的转化,在直角坐标系的大背景中,自然地想到设点坐标解方程解题,设出A(a,),关注AC与双曲线y=只有唯一公共点可以利用“∆”法或求导法.①设AC:y=kx+−ak与双曲线y=联立解公共点得方程kx2+(−ak)x−9=0,只有一个公共点则∆=(−ak)2+36k=0⇒k=−易得出C(2a,0),此时AC两点的坐标都求出了则S∆OAC=②直线AC与双曲线y=只有唯一公共点即相切,联想到求双曲线在A点的导数y′=也就是直线AC的解析式斜率,后面的解法就与上述类同.

从上述解法可以看出,殊途难归难在参数很多、十分繁琐,那是否有什么方法能够将其“秒杀”呢? 回归反比例函数的本质y=,k的意义是双曲线上的任意一点与坐标轴围成的面积为|k|,不难发现结果和这个k一样,两者有何联系吗?“k”实际就是图2中OB·AB=9,那么易得出2OB=OC,则看出三线合一,那么∆OAC是等腰三角形.这种是y=的特殊情况下,当比例系数为k又如何? 结论是否一致呢? 当双曲线的解析式为y=时,因为AC与双曲线相切,通过函数解析法求解得出xA=2xC,可以发现在∆OAC中三线合一,∆OAC是等腰三角形.

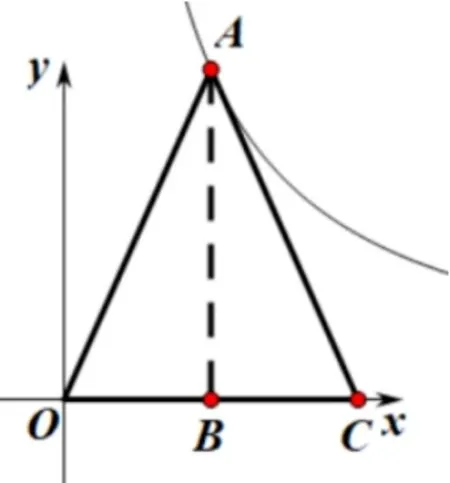
图2

设计意图在解决这幅直观上十分简单的图形所生成的题目时,运用解析法是一定能够解出的,但是可以发现解题过程中参数设得杂而多,十分繁琐.那么一个如此简单的基本函数模型就一定要用解析式法解决吗,还有更加简便的方法呢?

2 入木三分

上述案例不经意间生成了一个等腰三角形,为什么在双曲线与直线坐标轴能总是形成等腰三角形? 要想吃透这一数学性质,就要明白题目的生成,且看:

案例2如图3,直线y=mx交双曲线y=于A,B两点,点P为双曲线上一点,直线PA,PB分别交x轴于M,N两点,求证:PM=PN.

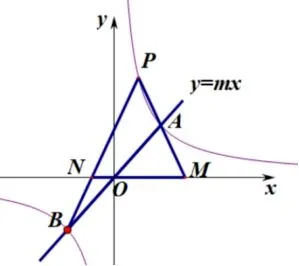
图3

抓住题中细节,给出了两个解析式便引导我们从以解析式的角度解决问题.解析法:A点是一个特殊的交点,设A(a,),由于图形的对称性,B(−a,−),P是双曲线上的任意一点,不妨再设出一个未知数,以不变应万变,P(b,),已知A点与P点的坐标可得lP A解析式y=同理lP B:y=分别令y=0 得出xM=b+a,xN=b−a,即得出xM+xN=2xP,得证PM=PN.

在不同的题目中发现都有类同情况的等腰三角形,他们之间有何联系吗? 看下图

不难发现在P、A两点的不断变换的过程中∆PMN永远是等腰三角形,然而当P点与A点重合的时候也就是部分“殊途同归”之时,这不就是案例1 中的原题再现吗? 也就是两个点在运动到特殊情况下形成了案例1,此时也是达到了部分同归即案例基础就是这个特殊情况.从双曲线的k的几何意义是一个矩形面积逐步生成等腰三角形,在直线与坐标轴相交的过程中发现隐藏的直角三角形斜边的中线,从特殊情形到一般情形,层层递进、双向可逆.

设计意图教学过程中需要教会学生能透过现象看清本质,从特殊现象思考到一般现象.不难发现解析式法的参数比上面的案例1 更多了,学生在利用这种解法时往往会因为参数杂多而失去了推演的动力,结果也只会不了了之,解析法只是单纯利用坐标的代数关系,并未利用到双曲线的本质,即万变不离其宗的“k”的意义.上述过程中都有等腰三角形的生成,几何方法在这里是否能用呢? 在这里想尝试运用直观的几何解法可计无所出,无法找出连接点,从而导致殊途难归.

3 苦心追求

在追求以“k”的性质将解题由抽象代数函数简化成直观的几何法时,首先明白双曲线是一个具有视觉诗意化的图形,他是具有对称性的,有一种规则美感.都说大道无形,可有时往往会表现出规则的形状,双曲线即是体现了这一点.而图形是在以x、y轴为渐近线的正中间,可以理解成曲线的“中点”(如下图4的弧BC中点)与原点是整幅图形的对称中心.等腰三角形也是一左右对称的图形,由于对称这一性质,那双曲线与坐标轴又有何关于对称而产生的联系呢?

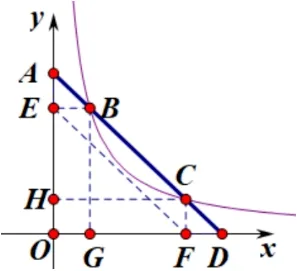
图4

案例3在如图4的双曲线的的背景下,直线AD交双曲线y=于B、C两点,求证AB=CD.在双曲线上,∵xB·yB=xC·yC=k,∴BE·化简得出AB=CD.

这种方法也只是利用了一下k的性质,解法也只是代数式,那么究竟如何追求到用纯粹的几何求解呢?

在图4中是否可以证明EF//AD? 放眼三角形中,S∆EBF=S∆EBG,S∆CF E=S∆F CH,可以得出他们的面积均为然而这两个三角形都有相同的底EF,得出AD//EF,同理如下图,连接HG、BH、CG,S∆BHG=S∆HGC=易得出HG//AD,放小了看直接得出四边形ABGH与四边形CDGH都是平行四边形,那么就得到AB=HG=CD.这边也就是用到了k的性质得出的面积不变.

设计意图在这里可以看出,解决这个问题的核心是“k”的性质,通过“k”与构造相似三角形以比例方程得出任意一条直线交双曲线同侧的两点及坐标轴的两点,就近的两点的距离是相等的,也就是图中的AB=CD.可以发现AB与CD就是上述所说以原点与双曲线“中点”为中心的对称线段,在以对称图形为背景中的线段也是有一定规律可循的.在等腰三角形中是邻边相等而在这AB=CD也可以看作邻边相等,那么,两者之间的联系究竟如何? 能否为几何法解题提供帮助呢?

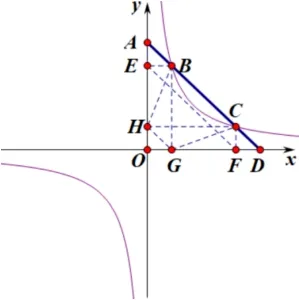
4 终成正果

案例2 几何法

观察图5与案例2 可谓是换汤不换药,题目中求解的PM=PN,实际上就是BF=BD,那么已知上述证得AB=CD,该如何求解呢? 又如何求得BF=BD的关系呢? 显然要证得∆BFD是一个等腰三角形,证明等腰三角形的方法有证明角相等、证明边相等、证明三线合一,可是放眼望去在这里面不是很好得出.试着用结论的角度反推,若∆BFD是等腰三角形,还能发现什么? 在这时我们的视角就不能仅仅局限于∆BFD,放眼望去在∆CBE中又能推出什么结论呢,做BC的中点连接OH,可以发现OH是∆CBE斜边BE的中位线,即OH//BF.转向∆BFD中又可以发现两个三角形相似,一个套一个地相似,若结论BF=BD成立,那么OH=DH也一定成立,如何证明,这时候我们的惯性思维就往往定格在了下面的两个三角形上而无法关注到直角坐标系本身是一个直角三角形,在Rt∆AOD中很清楚地看出,OH是斜边AD上的中线,易得出OH=HD进而推出BF=BD,那么案例2 的结论就得出了.

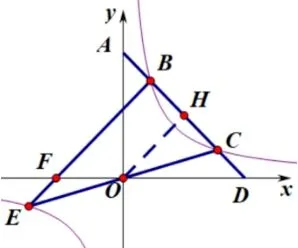
图5

情境对比案例1 和2 都是双曲线上的动点,联系k的性质进而阐述开的一系列问题.可以说图1是图5的特殊情况,因为图5中的AD直线与双曲线有两个交点,当他与双曲线相切也就是只有唯一一个公共点的时候就是上述的特殊情况了.而不难发现图1的OA=OC,也就是图5中BE经过原点O的情况下所产生,所以这是动点的特殊状态,是两个关于双曲线对称的点“合二为一、殊途同归”的结果.如图6到图8的演变过程.

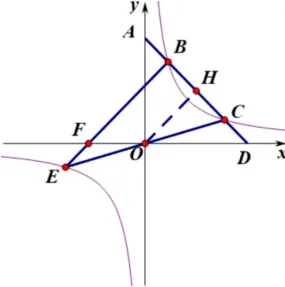
图6

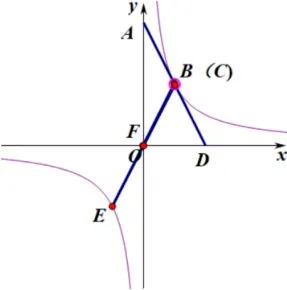
图7

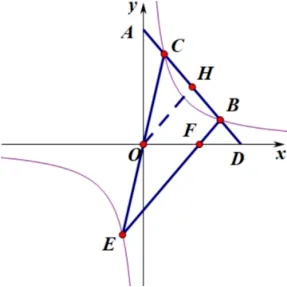
图8

这就是从图形一般到特殊再到一般的过程,在变化的过程中不难发现双曲线上特定的点与x轴所构成的三角形都是等腰三角形,OH是隐藏的中线.但由于双曲线有着对称性,在y轴上形成的三角形也有着等腰三角形.从演变的过程体现出特殊与一般的变化美,双曲线的对称美,构成定律的法则美.

设计意图教给学生最基础的数学本质,每种题目都有起源地,尤其是基本概念与基本性质,但述其根源还是最原始的定义.此题的核心就是反比例函数“k”所具备的性质.让学生真正领悟数学中蕴含的艺术,在学习数学中开拓自己的思维,从而达到培养学生数学核心素养的目标.

5 教学目的

5.1 教育教学首先是人的教学

加里宁曾说“很多教师常常忘记他们应该是教育家,而教育家也就是人类灵魂工程师.”教师教学是有价值有意义的,不仅仅只是教会学生解几道题、掌握一定技巧方法,而是从中学会做人的道理,通过克服困难、解决问题,培养学生坚韧不拔的毅力以及顽强拼搏的信心,使其从不会解到突破思维惯性障碍.追求用k的性质解题就是这种咬定青山不放松的努力,教师应帮助学生树立正确的价值观作为执教理念,从而真正成为人类灵魂的工程师.在这里从学生的思维出发,对于解析法如何从令学生繁琐的多参数变成单参数,从由k产生的代数变成纯几何法,都需要教师的精准提炼,不仅教会学生此题如何解,更是教学生如何明白解题的目的.

对于学生个体而言,价值观的教育是培养其成为一个人,成为一个更好的自己.孔子早就谈过人的四种基本素质“兴、观、群、怨”,兴,激发人的生命力,在这具体就是指如何发现双曲线与坐标轴构成等腰三角形,如何发现其中蕴含的数学思维;观,提高人的观察力与判断力,怎样观察、抓住题目中的细节,不放过任何一个蛛丝马迹,判断哪个条件是对解题有用,哪些是累赘、可有可无的;群,培养人的责任心,具有对题目把控的整体意识,能发现题目是如何生成,例如如何完成上述的从殊途难归再到殊途同归,发现两个动点移动,从一般到特殊、从群体到个体的大局观;怨,启发人的独立思考的能力,抛出问题后让学生能否独立思考解决,给学生k的性质,在这题中怎么用、如何用、为什么这么用、得出什么结论.这才是真正意义上的素质教育.

5.2 教学是质疑释疑的过程

没有疑问,学习教学就无动力而言.通过设疑创趣,即学生在没有问题时通过创设情景、激发学生思考的兴趣、触起灵动,产生问题,再试着把问题一层推进一层形成蝴蝶效应,促进研究问题的深入、促使思维深度的发展.可以利用苏格拉底提问,即产婆术:在教学生的过程中,并不直截了当地把学生所应知道的知识告诉他,而是通过讨论问答、变式训练等方式来使学生产生学习兴趣、积极思考,逐步引导学生自己最后得出正确答案的方法.在本题中,提问:直线的解析式的核心是什么?“比例系数k与截距b”,双曲线的核心是什么?“解析式k的本质”,两者的联系是什么,为什么会总是产生等腰三角形? 解析法如此繁琐,能不能用几何法、面积法求解呢? 激发学生对这些提问的思考与学习兴趣.最后通过变式等方法引导学生一切的一切都是归源于双曲线k的性质.通过多感官角度把问题看深入再挖掘问题,如从大局到部分、从一般到特殊、从群体到个体,解决原有问题,继续研究新产生的问题,这样层层递进、一环扣一环,形成一个良好的教育教学系统.

5.3 教学最重视过程与发展

《教父》中一句经典:花一秒钟能看透事物本质的人和花一生也看不透事物本质的人自然是不一样的命运.在平常的教学中不光要关注教育结果,更要重视过程,成功不是一蹴而就的,是要通过一定漫长的过程而达成的.在教学过程中,知识概念是输出,学习的过程中只是单一得输入而不输出,学到的东西就很难消化吸收,只有输出,以输出倒逼输入,学习的效果才会好.在本题中只知道双曲线和直线解析式形式、表象是远远不够的,在教师灌溉了这些知识后,应帮助学生不断探索、解决问题,将所学的整合成自己所特有的知识概念,消化成输出量,再在学习过程中注重这一概念的应用.当然学生不仅要知道如何解决问题,更应理解其本质内涵,充分理解知识原理,反反复复推敲、深有体会才会更好地解决问题,才能把问题看深看透.因为有时我们不可能在问题之内找到答案,答案往往在问题之外.当我们的视角站位发生变化或者是把问题上升到一个新的、更高的、不一样的层面时才有可能得出答案,而这一层面很有可能就是原理.注重k 的本质可以延伸出多种变式,通过对比得出异同点,从厚积薄发到顿悟,将一系列的双曲线问题看透,真正做到知识活用、一通百通,学生的思维会应思考原理本质而发生变化,大脑结构和功能也会因此改变.