递推数列通项公式问题中的待定系数法

李富春

(云南省玉溪第一中学 653100)

给出数列递推关系求数列通项公式是高考中的重点，也是难点.运用待定系数法构造等差、等比、常数数列是求解此类问题的常用方法.那么问题是怎样待定？在什么样的递推关系下待定一个系数？二个系数？三个系数？对此问题，本文作一些归纳、探究，供大家参考.

在这里，为了方便理解记忆，分别把引入一个等待确定的字母系数的值的方法叫做单待定系数法，简称“单待定法”；引入二个等待确定的字母系数的值的方法叫做双待定系数法，简称“双待定法”；引入三个等待确定的字母系数的值的方法叫做三待定系数法，简称“三待定法”.

1 单待定法

求形如递推关系an+1=pan+q(p，q均为常数，且pq≠0)和an+1=pan+qrn(p，q，r均为常数，且pq≠0，p≠r≠1)的通项公式，均可用“单待定法”求解.

例1 已知数列{an}中，a1=1，an+1=2an+3，求数列{an}的通项公式.

解析设an+1+λ=2(an+λ)，

则an+1=2an+λ.

因为an+1=2an+3，所以λ=3.

故an+1+3=2(an+3).

又a1+3=4≠0，于是数列{an+3}是首项为4，公比为2的等比数列.故an+3=4·2n-1.

所以an=2n+1-3.

例2 在数列{an}中，a1=6，an+1=2an+3·5n，求数列{an}的通项公式.

解析设an+1+x·5n+1=2(an+x·5n)，

则an+1=2an-3x·5n.

因为an+1=2an+3·5n，

所以-3x=3.

解得x=-1.

从而an+1-5n+1=2(an-5n).

又a1-5=1≠0，所以数列{an-5n}是首项为1，公比为2的等比数列.故an-5n=1·2n-1.

所以an=2n-1+5n.

2 双待定法

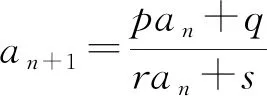
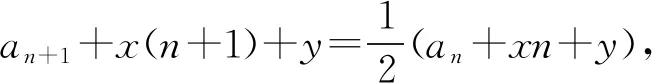
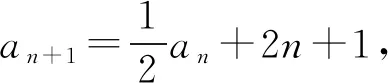
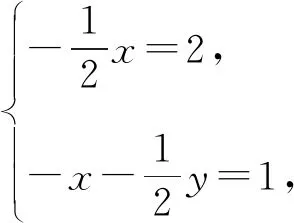
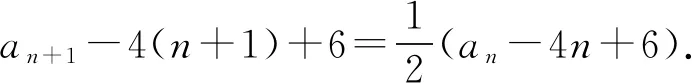
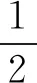
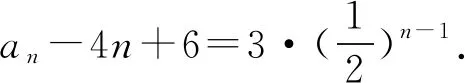
故而an=3·21-n+4n-6.

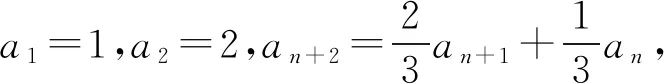
解析设an+2+san+1=t(an+1+san)，

则an+2=(t-s)an+1+stan.

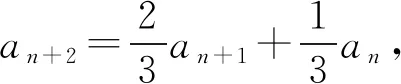
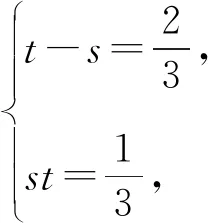
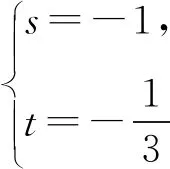
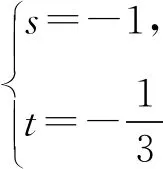
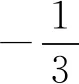
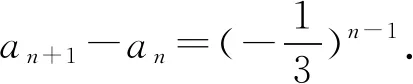
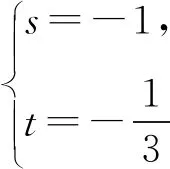
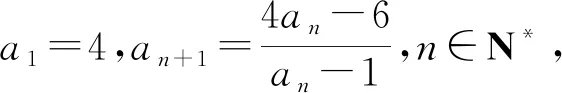
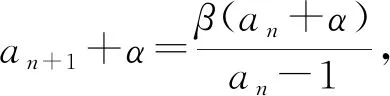
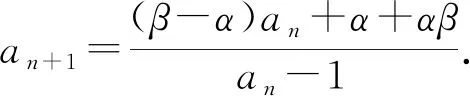
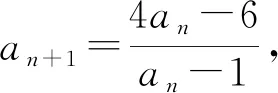
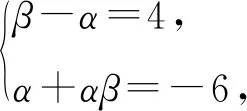
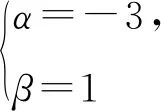
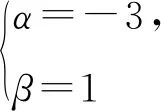
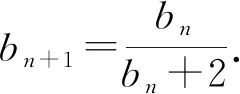
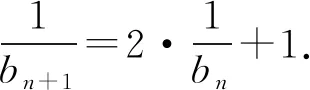
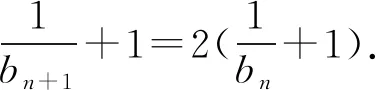
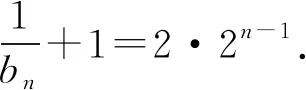
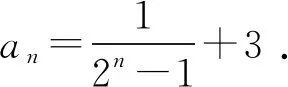
评注若取α=-2，β=2也可获解，同学们不妨试一试.

3 三待定法

求形如递推关系an+1=pan+qn2+rn+s(p，q，r，s均为常数，且p≠0，q≠0)和an+2=μan+1+λan+f(n)(μ，λ均为非零常数，f(n)为关于n的函数)的通项公式，均可用“三待定法”求解.

例6 在数列{an}中，a1=1，an+1=2an+3n2+4n+5，求数列{an}的通项公式.

解析设an+1+x(n+1)2+y(n+1)+z=2(an+xn2+yn+z)，则

an+1=2an+xn2+(y-2x)n+z-x-y.

因为an+1=2an+3n2+4n+5，

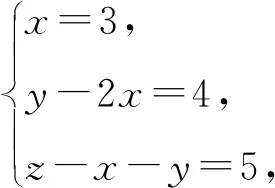
故递推关系an+1=2an+3n2+4n+5

可化为an+1+3(n+1)2+10(n+1)+18=2(an+3n2+10n+18)，

所以数列{an+3n2+10n+18}是首项为32，公比为2的等比数列.

于是an+3n2+10n+18=32·2n-1.

从而an=2n+4-3n2-10n-18.

例7 已知数列{an}满足a1=1，a2=2，且an+2=2an+1+3an+2n，求数列{an}的通项公式.

解析设an+2+xan+1+y·2n+1=z(an+1+xan+y·2n)，则

an+2=(z-x)an+1+xzan+(z-2)y·2n.

因为an+2=2an+1+3an+2n，

故an+1+an+2n=5·3n-1.

①

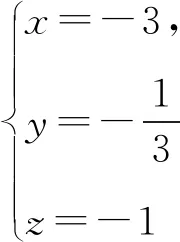
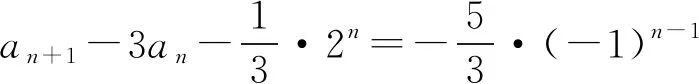
②

由于数列的递推关系形式多变复杂，从而求解数列的递推关系的通项公式解法灵活，由此使不少同学深感困难.若能掌握上述三种策略，可以说，解决这类问题就没有问题了.