基于RSSI 的井下人员定位算法改进
2023-03-17倪云峰王志刚
倪云峰, 王志刚, 王 静, 郭 苹
(西安科技大学 通信与信息工程学院, 陕西 西安 710699)
0 引言
我国是一个煤炭资源比较丰富的国家,而且在未来相当长的时间内煤炭资源依然是我国的主体能源。 受地理环境的限制,煤炭的开采大都在地下进行。 近年来,国内外井下安全事故频发,地面救援工作人员往往无法快速掌握煤矿井下被困人员的具体情况,救援工作缺乏可靠信息,这就导致救援方案无法达到最优,进而直接导致救援被困人员工作效率低,成功率小[1-2]。 因此煤矿井下人员定位算法的研究对生产安全、井下人员和设备的管理和调度以及建设智慧矿山有重要意义。 然而,与理想环境不同,煤矿井下环境较为复杂,信号在传播中会产生散射、衍射以及多径效应,往往导致接收端接收到的信号可能是多路无线信号和复杂环境中噪声相互影响的矢量和,进一步加剧测距定位偏差,定位精度下降。 在无线介质传感器网络定位中,根据定位时是否需要参考节点与未知节点之间距离信息,定位算法可分为基于测距算法(Range-based)和无需测距算法(Range-free)[3]。 目前,研究较为广泛的是基于RSSI 的测距算法,该测距算法较其他算法具有功耗小、成本低的优点,且不需要添加额外的硬件协作,适合井下无线定位的需要。
文献[4]使用中位数和最短距离法来获取对应节点RSSI 值的权值,并对其原始RSSI 值进行相应修正,得到最终RSSI 值,有效抑制RSSI 值的随机波动。 文献[5]采用测试两两距离之和的倒数替代两两距离倒数的和作为加权质心权重。 文献[6]提出了一种动态自适应调整权重系数的加权质心定位算法,首先对RSSI 测距算法进行优化,消除环境干扰影响,然后利用节点信息使待测节点自适应选取最优权值来提高定位精度。 文献[7]提出了一种基于RSSI 的四边形质心定位算法模型,使算法模型从三边扩展到四边,提高了定位精度。 文献[8]在原有三边定位的基础上,通过节点间数学转换改进为六点质心定位算法,仿真实验表明,定位精度显著提高。 文献[9]提出了一种基于RSSI 的混合滤波算法与最小二乘法估计相结合的测距方法,对RSSI 值进行了相应的误差修正,减轻环境造成的影响。 文献[10]提出一种基于质心与RSSI 信号比值相结合的混合加权质心定位算法,利用虚拟参考节点(即参考节点间的相交点)代替当前参考节点作为此处的参考顶点,节点间距离的比值作为加权的权值系数,该改进算法有效减轻了路径损耗指数n(与当前环境有关)的变化对定位精度的影响。
本文提出两圆距离之积的倒数作为权重系数对其相应参考节点进行加权处理的算法。 该算法以三边定位算法估计的节点坐标位置为基础,构建定位模型,求出相交区域坐标信息,最后结合加权质心算法实现对未知节点的准确定位。
1 基于RSSI 测距模型
1.1 RSSI 测距原理
基于RSSI 测距定位算法的传输模型主要有自由空间传输模型和对数路径损耗模型。 在煤矿井下较复杂环境下,由于多径效应等因素,自由空间传输模型难以满足定位精度的要求,因此在实际应用中常采用对数路径损耗模型,其传播模型为:
式中,P(d)和P(d0)分别表示接收端与发射端距离为d和d0时的接收信号强度值[11],d0一般取值1 m;n为路径损耗指数;Xσ为均值为0、标准差为σ的高斯随机变量,为所处环境中的噪声干扰。
在实际环境应用中,无线信号模型传输过程中普遍采用简化的信号衰减模型:
为了便于计算,通常情况下取d0为1 m,并用接收信号指示RSSI 表示P(d),用A表示P(d0),于是进一步得到:
进一步整理,可推出距离计算公式:
式中,A和n与当前实际环境有关,不同的环境对应的参数也是不同的[12]。 表1 为不同环境下对数路径损耗模型路径损耗指数n的相应经验值。

表1 路径损耗指数n 的经验值Tab.1 Empirical value of path loss exponent n
1.2 RSSI 信号值预处理
RSSI 测距定位原理是通过获取节点间接收信号强度值,利用信号传输模型来估算出节点之间的距离,通过已知参考节点信息利用几何关系计算出未知节点的位置[13]。 然而,RSSI 信号容易受到周围环境干扰,即使待测节点在同一位置,不同时刻接收到的信号值也可能出现较大偏差,因此需要对RSSI 信号进行滤波处理,去除变化较大的异常值,减轻环境造成的影响。 由于高斯滤波可以有效滤除信号中的异常值,使信号更加趋近于实际值以达到提高定位精度的目的,因此采用高斯滤波对RSSI 信号进行预处理。
当测距距离一定时,接收信号强度值概率分布可近似服从(μ,σ2)的高斯分布,其概率密度函数可以表示为:
式中,R为RSSI 值,
式中,Ri为第i次接收端接收到的信号强度值;n为测量次数。 根据高斯函数分布特性,在(μ-σ,μ+σ)为高斯分布的高概率发生区,对信号进行滤波,筛选出处于该区间的R值作为有效值[14],然后将该组有效值求和取其均值R—作为该待测节点所接收到的对应参考节点的最终RSSI 值(即修正后的RSSI 值),如式(8)所示,有效减轻复杂环境对信号的影响,改善信号传输模型的拟合度以及定位精度。
1.3 RSSI 测距模型参数修正
利用参考节点间的距离信息以及优化处理后的RSSI 值,通过最小化误差平方和对A和n进行拟合运算,以此来搜寻数据的最佳函数匹配,使各方程的误差达到一种平衡点,从而避免某一极端误差在其中起支配作用,动态修正路径损耗函数模型参数,有助于模型更加接近于真实的状态。 模型参数修正如图1 所示,其测距原理是:获取待测节点通信范围内所能接收到的参考节点的RSSI 值,根据滤波优化后RSSI 值大小选取所处环境中临近参考节点参与运算。

图1 模型参数修正Fig.1 Correction diagram of model parameter
A1,A2,…,Ak为O的临近参考节点,d1,d2,…,dk为各个参考节点到待测节点O的距离,根据式(3)可计算出各个参考节点到待测节点O的对应(i=1,2,…,k),建立测距方程组:
应用最小二乘法,可求出该区域内的A′和n′,带入式(4)可得修正后的测距模型进一步化简可得距离:
2 三角形质心定位算法模型
2.1 三边定位算法
三边定位算法利用选取待测节点附近合适的3 个参考节点参与逻辑运算进行未知节点坐标的定位,算法原理如图2 所示。

图2 三边定位算法原理Fig.2 Principle of trilateral positioning algorithm
已知未知节点O的临近3 个参考节点A,B,C坐标分别是(x1,y1),(x2,y2),(x3,y3),d1,d2,d3分别为参考节点A,B,C到待测节点O的测试距离。设未知节点O的坐标为(x,y),根据欧式距离公式建立距离方程组:
方程组经过变形和化简,可转化为矩阵形式:
式中,X = (x,y)T;;b =。带入式(12)可求得未知节点O的坐标位置:
然而在实际环境下,信号传输并非是这种理想状态,往往受到障碍物阻挡、多径效应和环境噪声的影响,导致距离测量出现一定的偏差,因此定位过程中往往并非交于一点。
2.2 传统质心定位算法
传统质心定位算法是利用待测节点与参考节点间的网络连通性[15-16],以参考节点所围成的多边形质心坐标位置作为未知节点的估计位置,传统质心定位算法示意如图3 所示。

图3 传统质心算法示意Fig.3 Schematic diagram of traditional centroid algorithm
待测节点O位于参考节点A,B,C三点所围成的三角形区域内,假设A,B,C三点坐标分别是(x1,y1),(x2,y2),(x3,y3),则待测节点O(x,y)坐标为:
2.3 改进加权质心定位算法
在实际应用中,由于受到复杂环境中多径效应以及障碍物的影响,信号实际接收到的信号强度与真实值存在误差,导致3 个圆相交于一个区域[17],所求的待测节点位置会有一定的误差,实际情况下的节点分布如图4 所示。d1,d2,d3分别为参考节点A,B,C到待测节点O的测试距离,O1,O2,O3为相交区域的3 个交点。

图4 实际情况下的节点分布Fig.4 Nodes distribution in actual situation
如图4 所示,未知节点O位于三角形ΔO1O2O3区域内,通过式(15)可求出O1(x1,y1)的坐标位置:
同理,可求出坐标O2(x2,y2),O3(x3,y3),改进加权质心定位算法,引入2 参考节点与未知节点距离之积的倒数作为权重系数对相应参考节点进行加权处理,则待测节点O(x,y)坐标为:
改进算法的具体步骤为:
① 参考节点周期性地向周围节点发送自身信息,即包含坐标位置和ID 信息的数据包。
② 在通信范围内,未知节点接收到超过阈值k个参考节点的信息数据包,重复读取5 次后进行高斯滤波得到最佳接收信号值,对滤波后RSSI 信号按从大到小排列,建立RSSI 值与参考节点位置的关系映射,得到参考节点与未知节点间的RSSI 集合:RSSI_set={R1,R2,R3,…,Rk},对应的参考节点位置集合:Position_set={(x1,y1),(x2,y2),(x3,y3),…,(xk,yk)}。
③ 根据式(10)可计算出未知节点与各个参考节点间的距离,对应集合d_set={d1,d2,d3,…,dk}。
④ 取出前3 个近基站对应的距离,结合对应参考节点坐标位置信息,根据式(16)改进加权算法求得未知节点O(x,y)的坐标。
3 仿真验证
选用Matlab R2020b 作为仿真测试平台来验证改进算法性能,网络定位区域为100 m×100 m 的正方形区域,分别布设100 个均匀分布的参考节点和50 个随机分布的待测节点,由于信号传播会受到井下环境的干扰,所以在仿真过程中加入均值为0、标准差为2 的高斯噪声,路径损耗因子n为3。 对传统质心算法、文献[18]算法与提出的改进算法进行比较,试验仿真定位节点分布和定位误差如图5 和图6 所示。
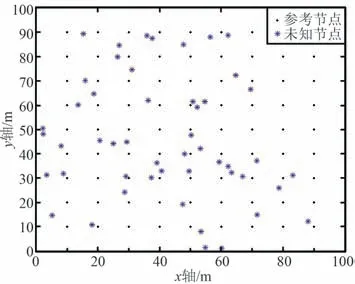
图5 节点分布Fig.5 Nodes distribution map

图6 定位算法误差Fig.6 Error of positioning algorithm
由图6 可以看出,改进的加权算法定位精度明显优于传统质心算法和文献[18]提出的算法精度。不同定位算法误差比较[19]如表2 所示。

表2 不同定位算法误差比较Tab.2 Comparison of errors of different positioning algorithms单位:m
由表2 可以看出,改进算法在最大误差、最小误差和平均误差3 方面都具有较大定位精度优势。 在平均误差方面,改进算法定位误差分别比传统质心算法、文献[18]定位算法精度分别提高52. 2%,38.5%,且定位平均误差在1 m 之内。 由此可知,改进算法具有更好的定位性能。
4 结束语
针对基于RSSI 定位算法在井下应用中受地质环境影响,定位精度低、稳定性差,无法满足井下高精度人员定位的需要的问题。 在不增加硬件资源的前提下,采用高斯滤波对数据进行滤波处理,减轻数据的波动及突变,为下一步的高精度定位提供基础。然后选取临近参考节点进行加权处理。 仿真表明,改进算法与传统定位算法、文献[18]提出的算法相比,定位误差明显下降,抗干扰能力更强,且该改进算法的平均定位误差为0.72 m,可基本满足井下人员定位精度要求。
