面向航天器返回舱测量任务的无人机航迹规划算法研究

刁晶晶, 胡守博, 施 岩, 李 乐, 胡锦明

(1.中国人民解放军63629 部队,北京102600;2. 中山大学 电子与通信工程学院,广东 深圳518107)

0 引言

我国的载人航天工程已经全面转入空间站在轨建设阶段, 在当前阶段及空间站建成后将会有大量的航天器返回任务, 届时航天器搜救任务将呈现高密度化[1-2]。 航天器返回舱进入大气层后着陆过程中的实景光学跟踪图像作为航天搜救信息网络中的重要信息节点,能够为着陆搜救态势的精准研判提供直观图像信息,有助于高效完成搜救回收任务。然而我国现有航天器返回舱的跟踪测控系统以陆基测控为主,受其测量特性影响,低仰角测量性能较差[3],且地面大型测控设备由于不具备快速机动能力,所以在实际任务中对航天器返回舱着陆段的测控覆盖能力通常较差。 针对航天器返回舱着陆段测量的实际情况,有必要引入搭载光学载荷的无人机对返回舱着陆过程进行实时景象测量,从而与陆基测控系统相互协同,构建出空地一体、相互补充、多元融合的搜救信息网络。 另外,航天器在返回过程受飞行控制精度、高空风等多种不确定因素影响,其弹道需要不断更新,尤其在弹道式返回过程中,实际弹道和理论弹道差异非常大[4],因此采用无人机开展返回舱实时景象测量时需要根据最新预测弹道快速规划生成符合探测要求的飞行航迹,对航迹规划的实时性提出了较高要求[5-7]。

目前的无人机航迹规划方法都是针对静态目标的侦察、打击和避障开展相关研究。 例如,有人利用混合整数线性规划检测威胁区域和障碍空间。 有人将复合矢量人工势场应用在航迹优化中,采用势场引力追踪目标,采用势场斥力远离障碍。 现有的无人机航迹规划技术缺乏适应于返回舱跟踪场景的快速算法[8-10]。 上述方法都缺乏针对航天器返回舱这种动态目标开展持续跟踪的快速航迹规划研究。

本文提出了一种基于“三进制”采样法的无人机航迹规划方法,在返回舱弹道预测已知的情况下,以无人机飞行性能和飞行限制区域为约束,以实时动态跟踪航天器返回舱为核心目标,充分考虑航迹规划方法实时性的同时,规划出跟踪返回舱的无人机飞行航迹,将无人机的机动作业特性和探测载荷有机结合起来,尽可能提升对返回舱的跟踪覆盖率。

1 航迹规划方法设计

1.1 总体设计思路

在航天器返回舱测量任务中,无人机需要考虑飞行速度、横滚角等飞行性能方面的约束限制,规避预定的禁飞区,在保证飞行安全的前提下,规划出无人机的最优飞行航迹[11-13],确保航天器返回舱进入大气层后尽可能处于机载光学传感器的工作范围内。

为了满足上述优化目标和约束条件,本文设计了一种基于“三进制”采样法的无人机航迹规划方法,包括初始化配置、初始航迹点计算、三进制航迹优化点的计算和航迹点稀疏4 个步骤。 整体规划如图1 所示。

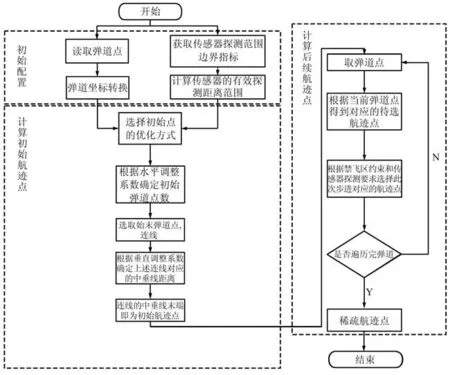
图1 基于三进制采样法的无人机航迹规划方法Fig.1 UAV trajectory planning method based on trinary sampling

1.2 初始配置

初始配置环节主要为航迹规划提供必备的数据支撑,并开展预先处理。 航线规划前提供的数据主要包括无人机预定跟踪弧段内返回舱的预测弹道点和无人机光学传感器的探测范围边。

弹道点用Ψ={L,B,H}表示,L,B,H分别表示返回舱在WGS84 系下的经度、纬度和高度,时间间隔为1 s。

传感器探测范围空间由最大探测距离ρmax、水平方位探测范围(Φmin,Φmax)、垂直俯仰探测范围(Θmin,Θmax)表示。 其中,Φmin为最小方位角,Φmax为最大方位角,Θmin为最小俯仰角,Θmax为最大俯仰角,最大探测距离根据目标特性和背景环境运用能量方程进行计算,

1.3 初始航迹点的计算

通常在航天器返回舱再入大气层后开始跟踪,此时航天器返回舱的速度大于无人机速度,为了达到更优的跟踪效果,无人机的位置应该在预测弹道点附近设置一定提前距离,提前距离与相对速度具有一定相关性,相对速度越大,提前距离越大,反之越小。

为了简化实际问题,假定航天器返回舱在水平面内的投影弹道短时间内近似为直线情况,如图2所示,图中v是目标的速度,v0是无人机的速度,q点为无人机的初始点,p点为航天器返回舱跟踪弧段内的弹道初始点。

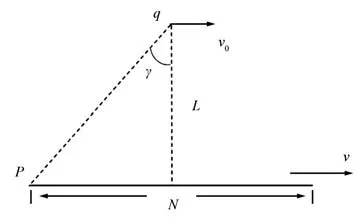
图2 初始点搜索方法示意Fig.2 Schematic diagram of the way searching initial point

可以得到如下公式:

式中,N为选取弹道点的数量;m为取点参数;L为期望距离;γ为最大方位角;v为目标速度。

无人机航迹规划点计算在巡航高度所处的水平面内进行研究,在飞行空域内选择一个基准点为坐标原点,X轴与正东方向一致,Y轴与正北方向一致,返回舱弹道点的XY坐标定义与上述情况相同。无人机航迹初始点对应的返回舱弹道起始点为G(0)= (x0,y0),终点为G(N)= (xN,yN),可得无人机航迹规划的起始点为:

式中,θ为弹道点连线的中垂线与横坐标轴的相对角度。

1.4 三进制航迹优化点的计算

计算后续航迹点时采用“一步一动”的思想,按照对标预测弹道点的方式,每隔1 s 向前推进一步,综合考虑禁飞区和无人机飞行性能的约束,计算出每个弹道点对应的最佳无人机飞行航迹点,从而能够随时根据返回舱的最新预测弹道点实时在线更新航迹点,满足航天搜救信息网络的观测要求。 以初始点为始发点,当前速度方向为步进方向,以无人机平均飞行速度为步长向前拓展一步,得到第二个航迹点,后续采用“三进制”采样法确定航迹点。

(1)确定待选航迹点

三进制航迹点采样示意如图3 所示。

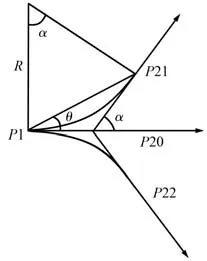
图3 三进制航迹点采样示意Fig.3 Schematic diagram of trinary trajectory sampling

P1 是当前已知航迹点,P21,P20,P22 是按照“三进制”采样法确定的3 个待选航迹点,这3 个待选点与原有飞行速度方向的夹角分别为α,0,-α。α根据飞机的最小转弯半径R计算,具体如下:

式中,Δt为飞机步进间隔;v为飞机速度。

P21,P20,P22 三个点的位置根据飞机飞行速度和偏转角度计算得出。

(2)设计禁飞区约束航迹点的代价函数

禁飞区的约束目标是整条航迹在保证一定跟踪覆盖率的前提下远离障碍物[14-15],若仅设置此约束条件,航迹优化将向远离障碍物的方向进行,无法在后续时刻进行持续跟踪,因此需要为此代价函数的启用时机加以限定。 避障示意如图4 所示,蓝色的圆为障碍物,外圈虚线与蓝色圆圈之间的区域为提前避障缓冲区,二者之间间隔距离为D0。 当待选航迹点在虚线外时,禁用此避障代价函数;当待选航迹点距离障碍物小于一定预测距离D0时,设置代价函数为激活状态进行航迹优化。 设计代价函数为:

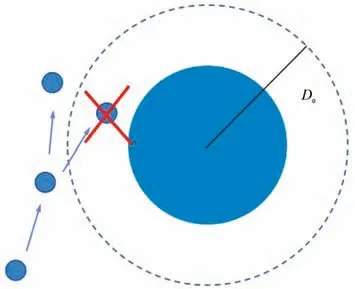
图4 避障示意Fig.4 Schematic diagram of obstacle avoidance

式中,dobs为待选航迹点与障碍物的距离;D0为预测距离;u(·)表示阶跃函数。

(3)设计光学传感器的探测约束代价函数

待选航迹点与返回舱弹道点的相对方位角为θ,则方位覆盖范围约束航迹点的代价函数为:

式中,opt(·)为传感器探测范围内的增益最大方向;θmin为最小方位角;θmax为最大方位角。

待选航迹点处无人机不存在横滚角时,无人机与返回舱的相对俯仰角为φ,此时俯仰覆盖范围约束航迹点的代价函数为:

根据数据分析，受访学生中75.22%的学生表示如果条件合适会选择创业，18.28%的学生表示表示毕业后会尝试创业。仅有6.5%的学生表示不会选择创业。从样本数据分析，当前高职院校的大学生占较大比例具有较强的创业意愿，因此，高职院校学生具有较强的专业实践技能，敢于探索和实践，高职院校毕业生也有望成为当前创业主力军之一。

式中,opt(·)为传感器探测范围内的增益最大方向;φmin为最小俯仰角;φmax为最大俯仰角。

另外,无人机转弯时两侧机翼具有一定高度差和升力差,即相对无人机的纵轴产生了一个横滚力矩,进而产生横向的方向偏移实现转弯。 无人机在转弯时横滚角将影响航迹规划中关于俯仰覆盖范围的代价计算,传统方法需要经过复杂的坐标系转换,才能得到无人机具备一定横滚角时观测返回舱的俯仰角,实时性较差。 为了提高运算效率,本文提出一体化横滚角迭代方法,能快速确定俯仰角数值,此时俯仰覆盖范围约束航迹点的代价函数为:

式中,opt(·)为传感器探测范围内的增益最大方向;φmin为最小俯仰角;φmax为最大俯仰角;g为重力加速度;Δt为飞机步进间隔;v为飞机速度;α为速度夹角。

(4)根据代价函数确定最优航迹点

计算总的代价函数cost:

计算出每个待选航迹点对应的代价函数,结果最小者对应的航迹点即为最优航迹点。

1.5 稀疏航迹点

无人机在飞行过程中航迹点设置得过多,不利于控制系统工作,因此还需要对上述航迹点进行稀疏处理,才能转化为符合无人机装订要求的信息。

航迹点稀疏示意如图5 所示。 若相邻3 点的转弯角度过大,则删去3 点中间的一点,使得航迹整体稀疏化,相邻3 点的转弯半径增大。

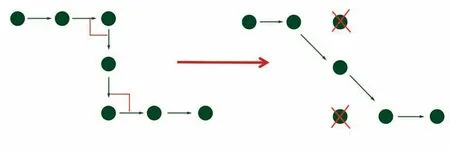
图5 航迹点稀疏示意Fig.5 Schematic diagram of sparse trajectory

直线处按照直线稀疏率选取下一个航迹点,若相邻3 点形成的转弯半径小于一定值,则采用曲线稀疏率选取下一个航迹点,以此循环直到遍历完整条航迹。 具体稀疏流程如图6 所示。

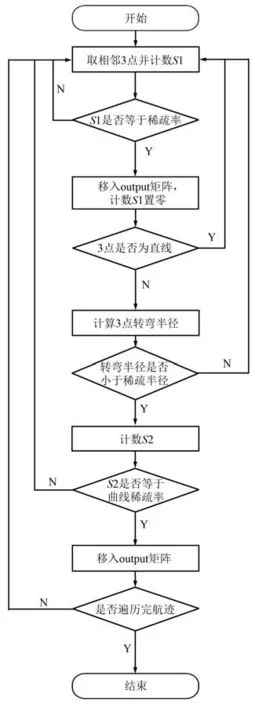
图6 航迹点稀疏流程Fig.6 Flowchart of calculating sparse trajectory

2 仿真计算

假定航天器返回舱在高度100 km 以6 200 m/s、-5°倾角向正东方向飞行直至着陆,在高度10 km以190 m/s 的速度开伞,开伞后飞行约10 min 着陆。 避障区域半径30 km,缓冲区外缘虚线距离避障圆圈10 km。 无人机光学传感器[16-18]的有效探测距离是400 km,俯仰角覆盖范围(-40°,40°),方位角覆盖范围(-70°,70°)。 为确保对航天器返回舱进行最高覆盖率的光学景象跟踪,应用本文提出的航迹规划方法,优化得到无人机的跟踪飞行航迹,如图7 所示。 光学传感器跟踪率可达99.86%,在有效避开障碍区的前提下,算法运行时间只有0.29 s,具有高实时性和有效性,能够有效满足应用场景。

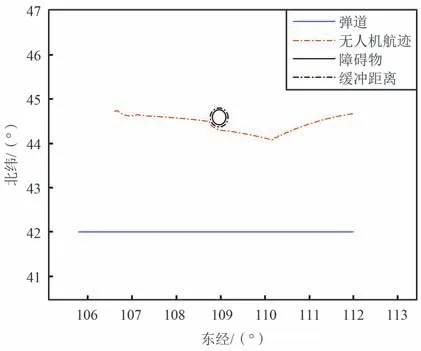
图7 无人机飞行航迹示意Fig.7 Schematic diagram of UVA flying trajectory

为了对比本文算法的有效性,选取了基础A∗算法及遗传算法作为传统航迹规划算法,将改进算法与2 种传统算法进行对比。 验证以下算法指标:

① 算法运行时间:用于验证算法的实时性;

② 传感器综合覆盖率:用于验证目标跟踪代价函数的有效性。

为了消除随机性造成的影响,采用 500 次蒙特卡罗实验进行验证。

由于传统算法缺乏自动初始化的方法,并且需要输入起始点及终点,因此本节采用快速初始化算法的思想确定基础A∗算法与遗传算法的起始点和终点,起始点设置为弹道初始位置附近,终点设置为弹道结束位置附近。 遗传算法采用3 个特征点作为航迹拐点,群体大小设置为50 个,进化失败迭代次数设置为10。 采用线性插值的方法将输出航迹点数插值到目标弹道点数,以此计算传感器综合覆盖率,如图8 和图9 所示。

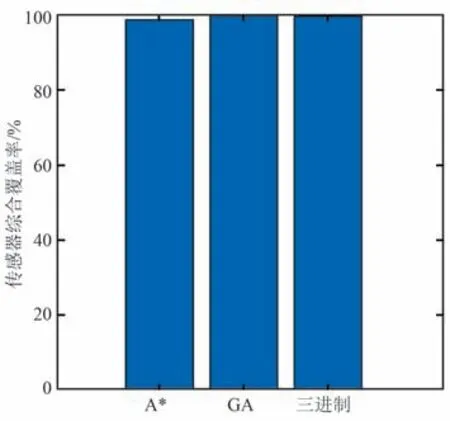
图8 3 种算法传感器综合覆盖率柱状图Fig.8 Bar graph of comprehensive sensor cover rate of three different algorithms

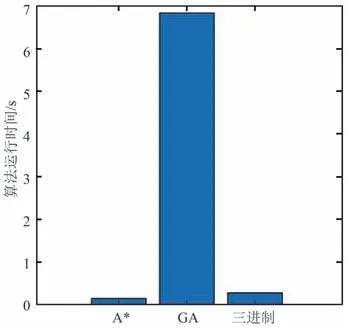
图9 3 种算法运行时间柱状图Fig.9 Bar graph of running time of three different algorithms

通过对比可以发现,遗传算法和三进制采样法均保持99%以上的覆盖率,能够达到覆盖要求;基础A∗算法、三进制采样算法运行时间短,实时性好;遗传算法运行时间长,无法保证算法实时性。 但实际使用中,基础A∗算法存在不符合飞行动力学约束的情况,因此实用性受限。 综上所述,本文提出的三进制采样法覆盖率高、算法实时性强,具有很好的工程实用性。

3 结束语

为了有效解决无人机对航天器返回舱再入大气层后的实景观测问题,本文提出了基于三进制采样的无人机航迹规划方法,能够快速确定合理地跟踪初始点,并将无人机飞行动力学约束融入航迹步进的采样机制,大大精简了航迹规划的可行解空间,同时采用了一体化横滚角迭代方法,减少了繁琐的坐标转换,从优化方法路线选择和计算处理上都充分考虑了实时性要求,与现有的传统无人机航迹规划方法相比,具有简单易行、工程实践性强和高实时性的特点,能够有效适应航天器返回舱测量保障任务中的无人机航迹规划问题。