公路边坡防护生态轻型桩最优间距分析

乔建刚， 刘 翔， 王 敏， 郭 飞， 王 月

(1.河北工业大学土木与交通学院， 天津 300401； 2.北京市政建设集团有限责任公司， 北京 100045)

随着我国经济迅速发展，山区公路建设步伐加快，自然环境下由于降雨等因素导致公路边坡失稳破坏的现象不断发生，危害行车安全[1].抗滑轻型桩技术可以较好地提高公路边坡抗滑承载力，被广泛应用于边坡安全防护中.目前关于抗滑微型桩的主要研究有：Zhang等[2]基于有限差分数值模拟方法，分析边坡和抗滑桩的受力和位移原理，确定抗滑桩的最优布置方案；Li等[3]综合考虑土拱整体力学平衡条件和强度条件，提出基于桩后或桩间土拱效应的抗滑桩最大桩间距计算公式，分析抗滑桩的最大桩间距控制因素；陈豫津等[4]以实际工程为依托，采用动力有限元法和强度折减法结合的方法，开展动力抗滑稳定分析方法研究；王飞等[5]通过大型振动台试验，对比分析地震波加载方向不同时，微型桩群不同位置加速度的响应，并对其护坡效果进行评价；Matsii等[6]针对单排抗滑结构中易滑土体与桩之间的相互作用，提出采用有限元法的分析方案，分析易滑土与桩相互作用的应力应变状态；Chen等[7]通过考察桩土相互作用机理，提出在极限状态下，桩背土拱只抵抗滑坡推力，根据Mohr-Coulomb强度理论和极限平衡理论，推导了桩间距计算公式；李绵绵等[8]通过对双排桩进行单独受力分析，推导桩身变形推力计算公式，又对双排桩治理后的滑坡进行二维模拟，分析滑坡的稳定性、应力与应变以及双排桩的弯矩与剪力；Liang等[9]采用机器学习优化微型桩设计，通过三排桩加固膨胀土滑坡，计算各桩的整体稳定性、滑动面的抗剪承载力和承载力；Rao等[10]通过评估考虑抗滑桩效应的非均质和各向异性边坡的稳定性，采用三维上限分析方法和强度折减技术，研究黏性- 摩擦土和纯黏性土中土体的非均质性和黏聚力各向异性对最优桩位和边坡稳定性的影响；Yan等[11]通过数值模拟软件FLAC3D，研究微型桩复合土钉支护的协同作用，分析微型桩不同间距下土体的位移场和应力场变化，得到微型桩与土钉复合支护的适宜间距.目前，国内外关于微型桩的研究多集中于固土效果、受力特性及作用机理上，对生态轻型桩桩间距的合理确定方法研究较少.生态轻型桩施工便捷、对边坡扰动性较小，是一种环境友好型的护坡方式.此外，其自身造价较低，护坡效果又可以满足工程需要，具有较好的应用前景.因此，开展公路边坡防护的生态轻型桩间距优化分析非常必要.

1 生态轻型桩定义与桩间距确定方法分析

1.1 生态轻型桩定义

生态轻型桩指由化学改性固土溶液、特殊处理的客土、植物根系等有机组成的自固结稳定桩.通过在边坡上按照特定直径和深度进行钻孔，再往孔内灌注化学改性固土溶液，待溶液被边坡土体吸收后回填特殊处理的适宜植物根系生长的客土，经过渗透溶液的改性作用使边坡一定范围内的土产生固结，植物根系由于趋养性率先在客土内部进行生长，而后逐渐沿化学改性固土溶液流经方向生长，最终形成有机组成的自固结生态轻型桩.生态轻型桩一般适用于土质复杂且难以满足植物生长要求的边坡，是通过改性土体自固结和植物根系固土等双重作用起到护坡的目的，与普通钢筋混凝土桩、钢桩、木桩等抗滑桩相比具有耗材较少、施工灵活、生态环保等优点，是一种兼具维持坡体稳定、绿化坡面环境的新型边坡生态防护技术.

1.2 生态轻型桩间距的影响因素分析

根据实际调查分析发现，发生破坏的公路边坡往往具有坡面较长、坡体较高等特点，坡度越陡、高度越高则边坡越不稳定[12]，生态轻型桩可以起到稳固边坡的作用，但单桩受桩深和桩径的影响，固土距离会受到一定限制，为实现生态护坡的功能，需对生态轻型桩间距进行优化分析，以达到桩群整体协同护坡的目的.生态轻型桩固土距离受多种因素的影响，变量较多且难以取舍，而MIDAS GTS NX软件可以迅速分析岩土结构，本构模型真实度高，功能分析全面可靠，能解决庞大、复杂和非线性问题.剪应力差分析法因其原理简单，而被广泛用于计算生态轻型桩一定范围内任意方向上的固土距离.因此采用MIDAS GTS NX计算机仿真技术，结合强度折减法分析生态轻型桩剪应力与距离、剪应力差与距离的变化规律，构建不同方向上剪应力差与固土距离的关系模型，通过凸轮模型综合固土强度最大原则确定凸轮最小内切圆半径作为生态轻型桩最优桩间距.

2 生态轻型桩固土模型建立

2.1 基本理论

土体在变形过程中弹性变形和塑性变形几乎同时发生，属于弹塑性材料，所以选取Mohr-Coulomb弹塑性模型对边坡土体进行分析.采用屈服面与塑性势函数不同的形式来模拟边坡土体，得到Mohr-Coulomb弹塑性模型如下.

1) Mohr-Coulomb模型的屈服面方程为

F=Rmcq-ptanφ-c=0

(1)

偏应力函数Rmc的定义为

(2)

式中：φ为Mohr-Coulomb屈服面在p-Rmcq平面上的斜角，一般指材料的内摩擦角；θ为广义剪应力方位角，且

(3)

摩擦角φ同样控制着材料在π平面上屈服面的形状，取值范围是0°≤φ<90°.当φ=0时，Mohr-Coulomb模型退化为与围压无关的Tresca模型，此时π平面上的屈服面为正六边形；当φ=90°时Mohr-Coulomb模型演化为Rankine模型，此时π平面上的屈服面为正三角形.

2) 双曲线型的塑性势函数控制方程为

(4)

(5)

式中：G为双曲线型的塑性势函数；Rmw为控制塑性势G在π平面上形状的参数；ψ为子午面上高围压时的剪涨角；c|0为初始黏聚力；ε为塑性势函数在子午面上的形状参数，一般取0.1；g为塑性势函数在平面上的形状参数.

形状参数g可表示为

(6)

椭圆形屈服面的外凸和光滑要求0.5<φ<1.0.

由Mohr-Coulomb弹塑性模型得到边坡土体应力与应变关系，认为当剪应力达到特定值时，边坡土体处于屈服状态.

2.2 参数选择及建立模型

以实际工程为依托构建三维立体模型，模型上下边界高16 m，前后边界长度为36 m，左右边界长度为20 m，边坡高8 m，坡顶边缘距右边界20 m，坡脚距左边界12 m，如图1所示.

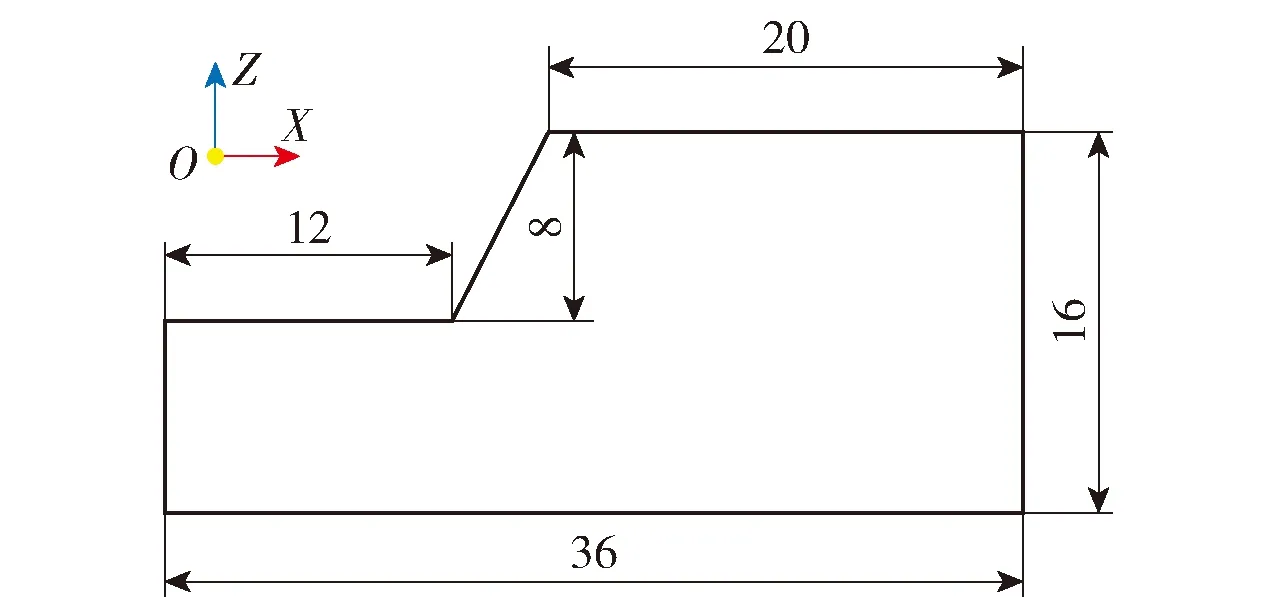
图1 边坡横断面示意图(单位：m)Fig.1 Schematic diagram of cross section of slope (unit: m)

左右边界采用Y向约束，前后采用X向约束，底面采用X、Y、Z三向约束.

将生态轻型桩布置于坡面上，桩心距边坡左右边界均为10 m，距上边界垂直距离4 m，垂直于坡面放入土体，桩径设为10 cm，桩长设为80 cm[13].通过剪应力来分析生态轻型桩对维持边坡稳定效果，认为当边坡土体的抗剪强度不足以抵消产生剪应力时，边坡发生滑移破坏，以桩心为原点，提取边坡横向、纵向和斜向上平行于坡面向下的剪应力，斜向为与横向的夹角为45°的方向，如图2所示.

图2 边坡模型及剪应力提取方向Fig.2 Slope model and direction of shear stress extraction

边坡模型材料参数如表1所示.

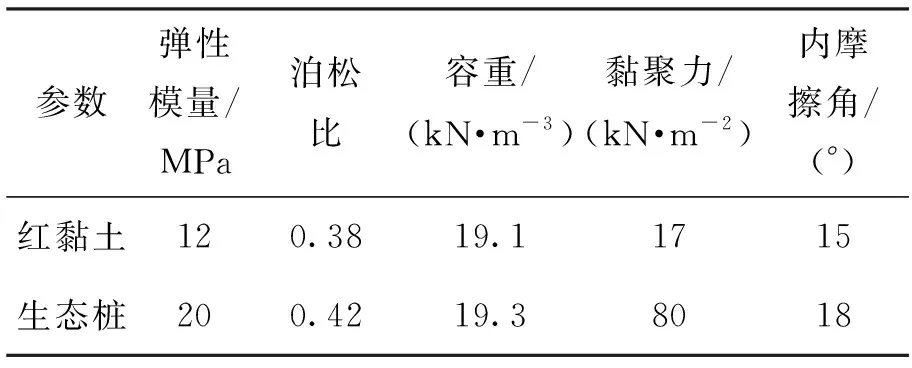
表1 材料参数

3 生态轻型桩间距确定

3.1 生态轻型桩纵向固土距离分析

由于重力对生态轻型桩纵向左右两侧土体的作用是相同的，故提取纵向一侧的剪应力进行分析.以生态轻型桩中心处为原点，与桩心纵向的距离为横坐标，坡体剪应力为纵坐标，分析有、无生态轻型桩时边坡坡体在纵向相同方向的剪应力和剪应力差与原点距离的关系，如图3、4所示.

图3 边坡纵向剪应力对比Fig.3 Comparison of longitudinal shear stress of slope

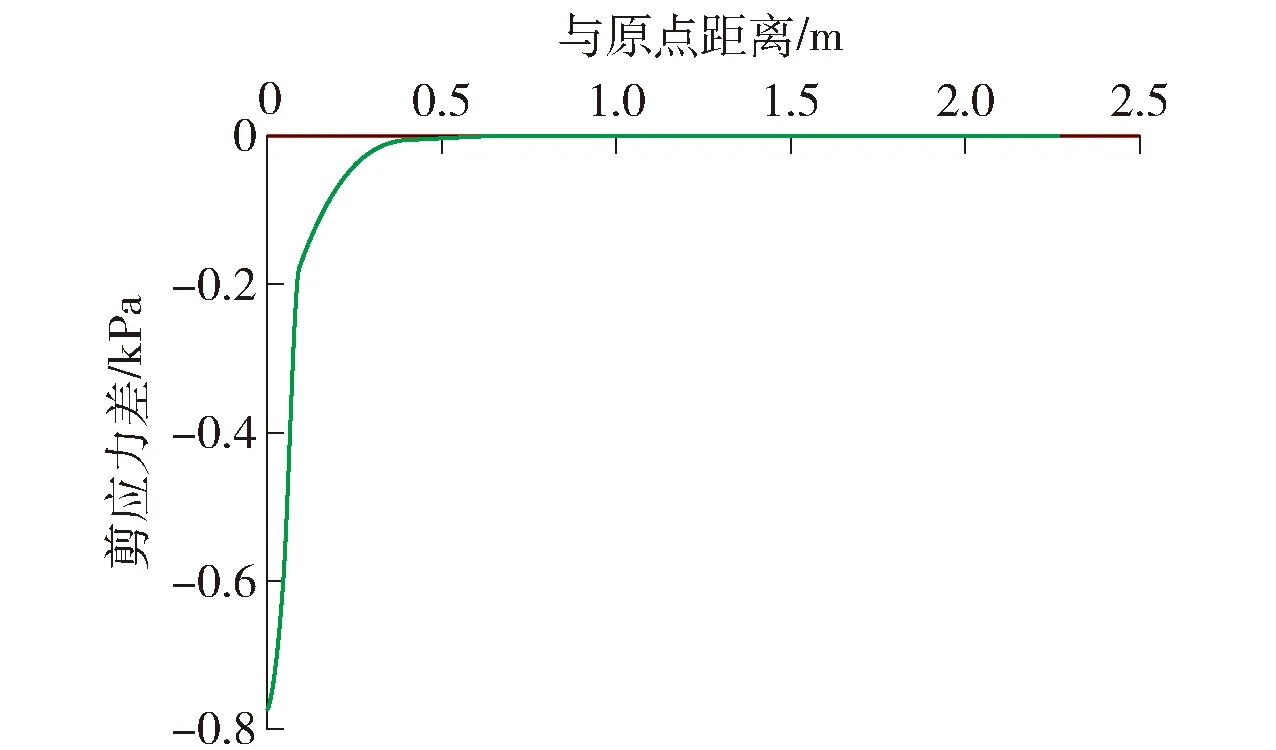
图4 边坡纵向剪应力差Fig.4 Longitudinal shear stress difference of slope

由图3可知，无生态轻型桩时，边坡在纵向上的剪应力为定值14.629 kPa，有生态轻型桩时，在生态轻型桩中心处的剪应力最小，为13.855 kPa，在纵向随着与桩心距离的增大，剪应力增加，当增加至与无生态轻型桩边剪应力相同后不变，说明生态轻型桩在边坡纵向一定范围内能起到减小坡面剪应力的作用.

根据图4中有、无生态轻型桩时纵向剪应力差进行分析可得，在纵向上，有生态轻型桩边坡的剪应力在距离原点0.45 m范围内小于无生态轻型桩的边坡，在0.45 m以外二者逐渐相等.在原点处有、无生态轻型桩边坡的剪应力差值最大，达到0.774 kPa，随着距离的增加，二者剪应力差值越来越小，直到距原点0.45 m时，剪应力差为0.将剪应力差值小于0的距离作为生态轻型桩在边坡纵向上的固土距离，因此生态轻型桩在纵向上的固土距离为0.45 m.纵向剪应力差与原点距离的关系符合模型

式中：y为有、无生态轻型桩边坡的剪应力差，kPa；x为选取位置与生态轻型桩中心点的纵向距离，m.对于式(7a)，R2=0.89，拟合效果满足要求.

3.2 生态轻型桩横向固土距离分析

3.2.1 边坡横向上部固土距离分析

同理，分别提取有、无生态轻型桩时边坡横向上部的剪应力，以生态轻型桩中心处为原点，与原点横向上部的距离为横坐标，剪应力为纵坐标，分析有、无生态轻型桩边坡在横向上部相同方向的剪应力和剪应力差与原点距离的关系，如图5、6所示.

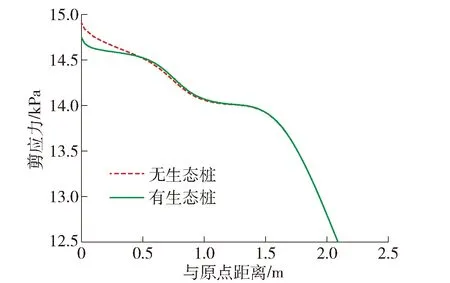
图5 边坡横向上部剪应力对比Fig.5 Comparison of transverse upper shear stress of slope

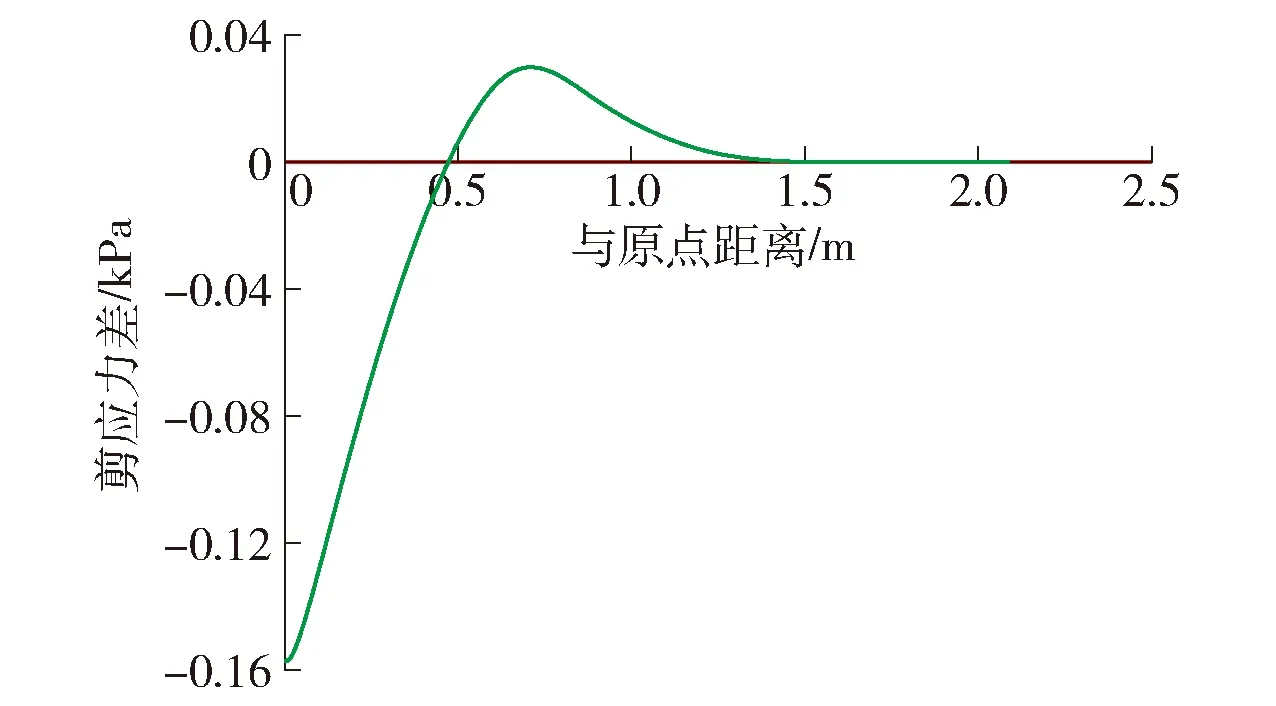
图6 边坡横向上部剪应力差Fig.6 Transverse upper shear stress difference of slope

由图5可知，有、无生态轻型桩时，边坡在横向上部剪应力变化规律基本相同，在原点处剪应力最大，随着与原点距离的增加剪应力波动式减小.无生态轻型桩时，剪应力最大值为14.907 kPa，有生态轻型桩时，剪应力最大值为14.750 kPa，说明生态轻型桩在横向上部一定范围内能减小边坡的剪应力.

对图6中有、无生态轻型桩横向上部剪应力差进行分析可得，在横向上部，有生态轻型桩的边坡剪应力在距原点0.40 m范围内小于无生态轻型桩的边坡剪应力，在大于0.40 m后剪应力曲线重合.有、无生态轻型桩的边坡剪应力差从原点开始增大，至0.71 m处时剪应力差达到最大，为0.043 5 kPa，而后开始逐渐减小，在1.37 m二者正差值减为0后趋于稳定状态.分析得生态轻型桩在横向上部的固土距离为0.40 m.横向上部剪应力差与原点距离关系符合模型

式中：y为有、无生态轻型桩边坡的剪应力差，kPa；x为选取位置与生态轻型桩中心点的横向上部距离，m.

对于式(8a)，R2=0.99，拟合效果满足要求；对于式10(b)，R2=1.00，拟合效果满足要求.

3.2.2 边坡横向下部固土距离分析

同理，分别提取有、无生态轻型桩的边坡横向下部剪应力，以生态轻型桩中心处为原点，与原点的横向下部距离为横坐标，剪应力为纵坐标，分析有、无生态轻型桩边坡在横向下部相同方向的剪应力和剪应力差与原点距离的关系，如图7、8所示.

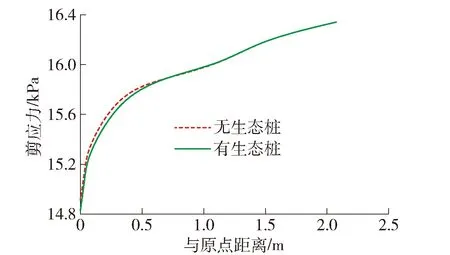
图7 边坡横向下部剪应力对比Fig.7 Comparison of transverse lower shear stress of slope

图8 边坡横向下部剪应力差Fig.8 Transverse lower shear stress difference of slope

由图7、8可知，生态轻型桩在边坡横向下部一定范围内同样可以起到减小边坡剪应力的作用.在距原点0.72 m范围内，有生态轻型桩的边坡剪应力小于无生态轻型桩的边坡，距原点0.87 m时二者剪应力差达到最大，而后逐渐降低，在1.28 m二者剪应力差为0 kPa后趋于稳定状态.生态轻型桩在边坡在横向下部的固土距离为0.72 m.横向下部剪应力差与原点距离关系符合模型

y=

式中：y为有、无生态轻型桩边坡的剪应力差，kPa；x为选取位置与生态轻型桩中心点的横向下部距离，m.

对于式9(a)，R2=0.91，拟合效果满足要求；对于式9(b)，R2=0.93，拟合效果满足要求.

3.3 生态轻型桩斜向固土范围分析

由于重力对生态轻型桩在边坡斜向上部左右两侧和下部左右两侧土体的作用都是对称的，因此只取一侧剪应力进行分析.

3.3.1 边坡斜向上部固土距离分析

分别提取有、无生态轻型桩边坡斜向上部一侧的剪应力，以生态轻型桩中心处为原点，与原点的斜向上部距离为横坐标，剪应力为纵坐标，分析有、无生态轻型桩边坡在斜向上部相同方向的剪应力和剪应力差与原点距离变化的关系，如图9、10所示.

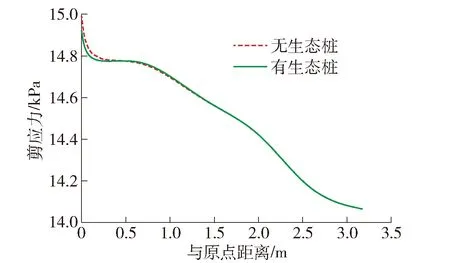
图9 边坡斜向上部剪应力对比Fig.9 Comparison of inclined upper shear stress of slope

图10 边坡斜向上部剪应力差Fig.10 Inclined upper shear stress difference of slope

由图9、10可知，生态轻型桩在边坡斜向上部一定范围内对减小坡面剪应力效果显著.在距原点0.44 m范围内，有生态轻型桩的边坡剪应力小于无生态轻型桩的边坡，距原点0.80 m处，二者正差值最大，在1.42 m后呈稳定状态，二者剪应力差为0.生态轻型桩在边坡斜向上部的固土距离为0.44 m.斜向上部剪应力差与距离关系符合模型

y=

式中：y为有、无生态轻型桩边坡的剪应力差，kPa；x为选取位置与生态轻型桩中心点的斜向上部距离，m.

对于式10(a)，R2=0.76，拟合效果满足要求；对于式10(b)，R2=0.94，拟合效果满足要求.

3.3.2 边坡斜向下部固土距离

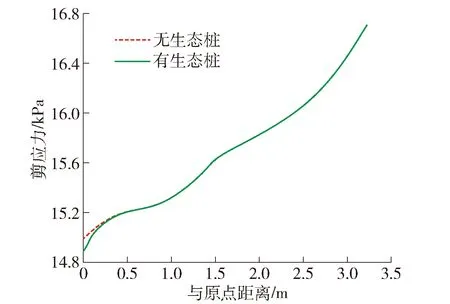
图11 边坡斜向下部剪应力对比Fig.11 Comparison of inclined lower shear stress of slope

同理，提取有无生态轻型桩的边坡斜向下部剪应力，分析有、无生态轻型桩边坡在斜向下部相同方向的剪应力和剪应力差与原点距离变化的关系，如图11、12所示.

图12 边坡斜向下部剪应力差Fig.12 Inclined lower shear stress difference of slope

由图11、12可知，生态轻型桩在边坡斜向下部一定范围内对减小坡面剪应力效果显著.在距原点0.64 m范围内，有生态轻型桩的边坡剪应力小于无生态轻型桩的边坡，距原点0.64 m后，剪应力差为0且不再变化.生态轻型桩在边坡斜向下部的固土距离为0.64 m.斜向下部剪应力差与原点距离关系符合模型

(11)

式中：y为有、无生态轻型桩边坡的剪应力差，kPa；x为选取位置与生态轻型桩中心点的斜向下部距离，m.

对于式(11)，R2=0.96，拟合效果满足要求.

3.4 生态轻型桩固土模型分析

由固土距离与剪力差分析可知，生态轻型桩孔径为10 cm时，可以得到生态轻型桩的固土距离模型为

y=-0.150 8×sin(0.997 7x+0.095 5)+0.555 9

(12)

式中：y为坡面不同方向固土距离，m；x为坡面不同方向与坡面纵向距离轴的夹角，rad.

对于式(12)，R2=0.83，拟合效果满足要求.采用F检验进行相关性检验，计算得到F0.05=161.085 9，查F分布表可得，F0.05(2,6)=5.14<161.085 9计算值F0.05=161.085 9，通过相关性检验，该模型显著相关.

生态轻型桩固土距离模型外部曲线如图13所示，曲线形似凸轮，故称为凸轮模型，其中A方向为坡面纵向，B方向为坡面横向.生态轻型桩孔径为10 cm时，边坡纵向的固土距离为0.45 m，横向上部为0.40 m，横向下部为0.72 m，斜向上部为0.44 m，斜向下部为0.64 m.为保证固土效果，根据固土强度最大原则，选取固土距离模型最小值为最佳固土距离，因此，确定孔径10 cm的生态轻型桩最佳固土距离为0.40 m，最优桩间距为0.80 m.

图13 生态轻型桩固土距离模型Fig.13 Soil-fixing distance model of ecological light pile

3.5 多级边坡生态轻型桩最优间距分析

当边坡高度较高或坡度较陡时，经常分级放坡，导致坡体不同位置承受的自重荷载也不同，底层边坡的不稳定概率也越大.因此，考虑自重荷载及边坡稳定性，以最高一级边坡为基准，可以得出三级边坡在坡度为1∶0.75、1∶1.00和1∶1.25，孔径为10、12 cm时的生态轻型桩的固土半径及设置间距，如表2所示.

表2 不同坡度及桩径下三级边坡生态轻型桩桩间距设计值

由表2分析可知，坡度、桩径和边坡等级都会对生态轻型桩的固土距离产生影响，孔径相同时，坡度越大，则桩距越小；坡度相同时，孔径越大，则桩距越大；级数越低的边坡，则桩距越小.考虑到生态轻型桩的不同桩径、边坡的不同坡度和分级放坡的影响，为提高模型的适用性，得到生态轻型桩固土距离模型为

y=k[msin(px+q)+n]

(13)

式中：y为坡面不同方向固土距离，m；x为坡面不同方向与坡面纵向距离轴的夹角，rad；k为植物根系指数，植物根系指数与植物类型有关，乔木取0.829 5，灌木取0.312 7，草本取0.254 8；m为边坡等级系数，取值范围-1～1，等级越高取值越小；p为边坡坡度系数，取值范围0～1，边坡越陡取值越小；q为生态轻型桩桩径关联系数，取值范围0～0.5，桩径越大取值越小；n为常数项.

根据固土距离模型，为保证生态轻型桩对边坡整体的防护效果，对模型求解得到生态轻型桩的固土强度最大的距离为最优固土距离，即模型y的最小值，即ymin，最优桩间距为最优固土距离的2倍，即2ymin.

4 结论

本文通过数值模拟方法，分析生态轻型桩在坡面不同方向上固土距离与剪应力差的关系，并根据固土强度最大原则优化桩间距的设计，主要得到以下结论：

1) 分析了坡度、坡高和生态轻型桩间距对边坡稳定性的影响，并对生态轻型桩进行定义.

2) 采用MIDAS GTS NX软件，以Mohr-Coulomb弹塑性理论为基础，结合强度折减法对生态轻型桩防护下的边坡在纵、横和斜向剪应力差随距离的变化进行分析，得到各方向上的最优固土距离.

3) 在不同生态轻型桩桩径、边坡坡度和分级放坡条件下，构建生态轻型桩固土距离凸轮模型，得到生态轻型桩的最优桩间距，为公路边坡生态轻型桩的设计提出了一种新的思路.