基于多目标差分进化算法的机加工柔性作业车间调度
2023-03-17高元杰初红艳张彩霞刘志峰
程 强, 高元杰, 初红艳, 张彩霞, 刘志峰
(1.北京工业大学先进制造与智能技术研究所, 北京 100124;2.北京工业大学先进制造技术北京市重点实验室, 北京 100124;3.北京工业大学机械工业重型机床数字化设计与测试技术重点实验室, 北京 100124)
调度研究的问题简单来说就是如何将稀缺资源分配,即将资源给在一定时间内的不同任务. 调度在大多数制造和生产系统及信息处理环境中扮演着重要的角色[1]. 目前关于调度的研究主要涉及模型建立和算法设计,其中问题建模主要研究调度模型、调度规则、目标函数等,而调度算法设计主要研究算法复杂性、算法收敛性、算法质量等[1-6].
目前,关于柔性作业车间的模型调度建立国内外都有相关的研究. Willian[7]作为调度理论的奠基人,提出了车间调度,开创了调度问题的理论研究工作. 针对多品种、多件数的工件调度难的问题,Low[8]和Chinyao等[9]在柔性作业车间模型的基础上考虑了分批调度,建立了柔性作业车间分批处理模型,基于其数学模型的研究表明:在作业车间中,通过分批处理可减少机床闲置时间和工件流动时间. Jeong等[10]在分批调度的基础上进一步建立单工艺路线生产车间动态批量分批作业计划,将生产辅助时间(setup times)和加工时间(process times)进行了区分. 与此同时,一种考虑返工的数学模型也开始被提出. 陈建国等[11]针对传统Job-Shop数学模型忽略返工及重加工的因素,构建了考虑该情形下的Job-Shop调度数学模型及相应的求解算法. 廖怡娜等[12]建立了考虑作业返工的资源受限项目调度问题的数学模型,针对该模型,设计了面向3种不同情况的修复算法. Ceylan等[13]针对多阶段供应链网络的特点,将多阶段供应约束考虑到模型中,建立了双目标混合整数线性规划模型,提出了一个新的协调调度. 目前调度模型研究主要围绕着设置约束条件和优化目标等进行研究,主要包括返工、批量、资源受限等约束条件和能耗、最大完工时间和最大延长时间等优化目标,但是大部分研究关于约束条件的设定较为简单,譬如文献[11]将返工率视为固定值,文献[10]的准备时间不受工序次序影响等. 而且在机加工中,刀具的成本往往也占很大的比重,且刀具也属于易耗品,但是关于以刀具作为调度优化目标的研究还较少,因此本文在前人研究的基础上,将机加工的常见约束如批量约束、基于贝叶斯条件概率求返工概率和受次序影响的准备时间等考虑至模型中,并结合机加工中的刀具损耗特点进行建模,提出一种新的机加工柔性车间调度批量模型,使模型更加符合实际生产需求,最终提出一种以最大完工时间、能耗和刀具损耗数量为优化目标,考虑返工、序列的准备时间和以批量作为约束的多目标机加工柔性作业车间调度模型,并采取差分进化算法进行求解.
1997年,差分进化(differential evolution,DE)[14]算法由Storn提出,其初衷是解决切比雪夫多项式问题. 作为一种基于群体导向的随机搜索技术,DE算法包括初始化、变异、交叉以及选择等操作[15]. 由于算法原理较为简单、参数较少、鲁棒性较好并且易于实现,因此已有部分研究应用于车间调度问题[16-17]中. 传统差分进化算法在解决本文提出的多目标机加工柔性作业车间调度模型时,由于随机初始化导致算法求解时间较长,在短期内不能得到较好的调度结果,同时由于生产条件的复杂性,机器差分运算得到的差分向量较差,因此需要进行一定的改进. 目前针对DE算法的理论研究主要集中在如何提高算法的寻优能力、收敛速度以及克服启发式算法常见的早熟收敛以及搜索停滞等缺陷方面[15],本文从模型特点出发,提出一种初始化策略和机器选择策略分别对差分进化算法的收敛速度和解的质量进行一定程度上的改进.
1 多目标机加工柔性作业车间调度模型
多目标机加工柔性作业车间调度可定义为:有N类工件在M台机器加工,每类工件包含若干道工序,每道工序再分成若干个任意大小的批次,工序可在多台不同性能的机器上进行作业操作,由于机器性能的不同,工序在不同机器上的加工时间是不同的,同时,能耗和刀具磨损也是不同的. 因此工序在不同的机器上加工,调度指标除了最大加工时间外,还有能耗指标和刀具寿命指标. 多目标机加工柔性作业车间调度所要解决的问题是:
1) 确定各个工件划分批次数量及各批次大小.
2) 确定各子批在哪台机器设备上加工.
3) 确定最优的工序加工顺序.
4) 在多约束条件下求得较优多目标调度方案.
1.1 变量定义
为了方便后续模型和算法描述,定义了下列相关变量用于描述数学模型.
N:工件类别数.
M:机器总数.
H:工序总数.
Ω:总的机器集.
i:工件类别号,i=1,2,…,N.
k:机器序号,k=1,2,…,M.
j:工序序号,j=1,2,…,H.
ni:每类工件的件数,i∈{1,2,…,N}.
Bi:每类工件的批数,i∈{1,2,…,N}.
li,b:每类工件的子批的工件数,b∈{1,2,…,Bi}.
ti,li,b,j,S:i类工件的li,b子批j工序起始加工时间.
ti,li,b,j,E:i类工件的li,b子批j工序终止加工时间.
ti,j,k,P:i类工件j工序在机器k上的加工时间.
ti,j,k,R:考虑返工的i类工件的j工序在机器k上的加工时间.
ri,j,k:i类工件的j工序在机器k上的加工不合格返工概率.
Xi,li,b,j,k:如果i类工件的li,b子批的j工序在机器k加工则为1,否则为0.
tk,C:机器k上最后一个子批工序的完工时间,k=1,2,…,M.
tCmax:最大完工时间.
1.2 数学模型
模型以优化最大完工时间、能耗和刀具损坏数为优化目标,首先建立批量约束.
每类工件分批后,该类工件的每个子批的工件数量之和为该类工件的总件数.
(1)
根据Xi,li,b,j,k的含义可知,每类工件的子批的每道工序同一时刻只能在一台设备上进行加工.
(2)
各子批在加工时存在工序先后顺序约束,tsetup为加工前准备时间,取决于上一工件和目前工件的类别.
ti,li,b,j+1,S≥ti,li,b,j,E
ti,li,b,j,E=ti,li,b,j,S+tsetup+ti,j,k,R×li,b
(3)
考虑到加工过程中不合格返工现象常有发生,将返工这一动态问题转换为静态问题进行处理,在已知ti,j,k,P的基础上为返工预留加工时间
ti,j,k,R=ti,j,k,P+ri,j,k×ωP
(4)
式中ωP是由MES系统中的历史数据所得,表示考虑不同概率下加权的返工修复时长.
通过统计可以常见地求得加工条件不合理的先验概率:P(X=A)、P(X=B)、P(X=C).其中X表示加工条件不合理的随机事件,A、B、C分别表示人操作不规范、毛坯不合格和机床加工性能不达标事件.
进一步地,经过统计可以获得在加工条件不合理时,工件不合格的条件概率:P(Y=不合格|X=A)、P(Y=不合格|X=B)和P(Y=不合格|X=C).最后根据统计的先验概率和条件概率,计算当工件出现不合格时,各种加工条件不合理情况发生的后验概率,并基于后验概率和各种加工条件不合理的情况下的平均修复时长,通过概率加权设计预留的返工时长,其中tR,person、tR,workblank、tR,machine表示统计所得在各种不合理条件下进行修复的平均时长.
ωP=P(X=A|Y=不合格)×tR,person+
P(X=B|Y=不合格)×tR,workblank+
P(X=C|Y=不合格)×tR,machine
(5)
最后让ti,j,k,R与子批li,b工件数量相乘,表示i类工件的子批li,b的j工序在机器k上的加工时长.
因为工件在机器的准备时间取决于上一工件,因此考虑带有工件次序的准备时间,tMatrix为考虑序列准备时间矩阵,其中行与列表示工件和工件之间如果在机器上相邻时,切换工作环境的准备时间.

(6)
最大完工时间取决于机器最后一个子批完工时间的最大值, 即
tCmax=max(t1,t2,…,tM)
(7)
以最后一个子批完工时间为优化目标:min(tmax),同时为考虑机床机加工过程中的能耗,建立了模型[18]
Ek=Pk,ftk,f+Pk,airtk,air+Pk,vtk,v
(8)
式中:Pk,f、Pk,air和Pk,v分别表示机床k待机功率、空载功率以及切削功率; 而tf、tair和tv为其对应的时间.
此机加工能耗模型,主要由3个部分构成,分别是待机能耗、空载能耗以及切削能耗.
Pk,air与主轴转速相关, 且
Pk,air=An2+Bn+C
(9)
式中A、B、C取决于机床特性和主轴转速.类似地,Pk,f和Pk,v也取决于机床特性,可通过实验观测求得.
因此,可以得到
(10)
以能耗作为优化目标:min(Etotal),同时应注意,在切削速度增大的同时,依据文献[18]给出的模型,可以推测得出切削速度增大尽管能缩短加工时长,但是却会一定程度上增加能耗的结论.
由于在机加工过程中,机床在给定的工艺参数下,刀具寿命是固定的,以铣削的方式进行加工的刀具寿命[19]
(11)
式中Ti,j,k表示i类工件的j工序在机器k以确定的工艺参数加工下刀具的寿命.工艺参数中Vc为切削速度,fz为每齿进给量,ap为轴向切深,ae为径向切深.
在文献[19]中,所求得的b1、b2、b3、b4分别为-2.929 8、-1.912 8、-1.511 9和-1.141 3,这表明切削速度对刀具寿命影响非常显著,实际经验表明切削速度越大,切削区温度越高,刀具磨损程度越大,刀具寿命越短,这与所求得的公式是一致的.
考虑到刀具也有成本,通过计算在此工艺下子批的累计加工时长,让累计加工时长除以该工艺下的刀具寿命,可大概估算出预计耗费刀数
(12)
式中Ni,j,k,tool为所有i类工件的子批的j工序在机器k上加工累计耗费的刀具数,通过对每个设备实际加工时间进行累加求和,然后将累加求和的时间除以刀具预估寿命即可求得.
因此考虑所有子批的刀具磨损情况,以刀具损坏数量为优化目标
其余假设条件如下.
1) 已知每类工件总批量数,划分子批后每批次的工件在一起加工.
2) 同种工件每个子批的每道工序可以选择不同设备进行加工.
3) 每台设备在同一时刻只能加工某类工件某批次的一道工序.
4) 某工序一旦于设备上开始加工,不允许中断.
2 差分进化算法设计
考虑到传统差分进化算法在本文调度模型的应用上效果不佳,为得到较优解,在传统差分进化算法的基础上进行一定的改进,主要对初始化策略和差分操作进行改进.
2.1 编码方式与解码方式
本文采取以工序为基准的编码方式,以10个工件5道工序6个机器为例,总工序为10×5=50道工序.为50道工序分配机器,因此染色体中还需要为50个工序预留50个机器位置,染色体总长度为100,为方便解码,设定染色体前一半部分代表的是工序,后一半部分代表的是加工该工序对应的机器,其中染色体机器位置部分第1~5个位置表示工件1的第1道工序到第5道工序所选择的机器,第6~10个位置表示工件2的第1道工序到第5道工序所选择的机器,以此类推,如图1所示.

图1 编码图Fig.1 Coding diagram
工件的个数计算方式为
(13)
表示将每个子批作为一个工件视为调度,因此确定好如何分批和每批的批数问题也是本文关注点之一.考虑到当使用等分批不能使结果更加优化时,才考虑用其他分批策略[20],因此采用等分批进行分批,为确定批数,根据经验所得划分的批次判定公式[21]进行批数确定.
(14)
式中:Tz为考虑分批的时间参数,即最小加工时间;H为工序数;l为批数;tj为某工件第j工序的加工时间;tL为最长工序的加工时间;Kz为子批中包含的工件数.
分批算法的基本流程如下.
1) 初始化参数,令x=1,n=1,x表示工件类别,n表示批数.
2) 将x分成n批,按式(14)求得Tz,即此类工件分批时间参数.
3) 若n 4) 计算批数为1,2,…,nx批的时间参数Tz. 5) 从4)计算得到的一组Tz中找到最小的Tz,存储并输出此时的批数n. 6) 若x 解码时将染色体中的工序部分编码和机器部分编码分别与加工信息表一一对应,如表1所示,可获取每类工件的每道工序的加工时长和能耗信息,并将其代入各个适应度函数进行求解,进行解码. 表1 5种类-4工序-6机器加工信息 在实际生产中,调度常常需要满足多目标的任务需求,为此,需要将多个目标进行综合考虑,本文考虑各目标的单位成本生成多目标适应度函数 Ftotal=Ctool×Ntool+Cenergy×Etotal+Ctime×tCmax (15) 式中Ctool、Cenergy和Ctime分别为对应目标的单位成本,可根据企业生产的实际情况获取,而Ntool、Etotal和tCmax可分别根据式(12)(10)和(7)求得. 传统差分进化算法中,使用随机初始化对种群进行初始化,种群的全局性虽然能够得到保证,但是个体质量较差,将导致迭代次数过多才能获得较优个体,为保证全局性,同时一定程度上提高初始种群的质量,本节在编码的工序部分采用随机初始化,而机器部分考虑到模型的多目标特点,提出一种综合考虑能耗和加工时间的轮盘赌初始化策略,这种初始化策略缩短了差分进化算法的运行时间,一定程度上改进了差分进化算法. 首先确定好种群个体的数量,之后,对每个个体进行以下初始化操作,初始化流程如下. 1) 工序初始化 根据工件分批的批数,确定工件数量,根据每工件的工序数量确定工序总数,例如工件共有15件,工序4道,生成4个1、4个2……4个15,然后将生成60道工序乱序处理,其中第1个1表示工件1的第1道工序,第2个1表示工件1第2道工序,以此类推,其余工件类似. 2) 机器初始化 ① 开始循环,令i=1. ② 循环读取已生成的工序部分,获取每工序的所有可用设备的加工时长和能耗,基于轮盘赌规则生成相应的数据矩阵. ③ 生成随机数,根据随机数在该工序对应染色体的机器位置查轮盘赌数据矩阵所对应的机器部分,为该位置赋值找到的机器.例如,某工件的工序1有3个机器可以选择,机器1、机器2、机器3对应的加工时间分别为6、3、2 h,而能耗分别为12、5、2 kW·h,此时基于自定义的轮盘赌规则,考虑模型中的优化目标能耗和加工时长,假设以0.75表示考虑能耗的权重,0.25表示考虑时长的权重,则该工序选择机器1进行加工的概率区间为 P1=[0~(6÷11×0.75+12÷19×0.25)] 类似可得到关于机器2、机器3的轮盘赌概率区间[0.567,0.838]、[0.838,1.000],可以得到轮盘赌矩阵(0.567,1),(0.838,2),(1,3).如若生成随机数0.80,根据矩阵,随机数在0.567和0.838之间,根据轮盘赌矩阵,此时使用机器2加工该工序. 为得到较优解,通过差分进化算法对初始化的种群进行更新,差分进化包括变异、交叉及选择, 算法流程如下. 步骤1算法初始化,生成最大迭代次数maxgen、变异因子F和交叉因子Cr. 步骤2开始循环,令i=1. 步骤3随机选择3个个体X1、X2、X3,并生成随机数rand,对X1、X2进行差分操作:首先生成随机数,如果随机数小于变异因子,则进行变异操作,子代向量为变异操作后的向量个体,否则子代向量为父代个体X1. (16) 式中G(X1,X2)表示父代个体彼此之间进行交叉,由于涉及工序和机器2个子问题,该差分操作较为复杂,具体如下. 1) 关于编码中的工序部分交叉采用优先交叉(POX),如图2所示:P1和P2为父代的2个个体,C1和C2为子代2个个体,P1和P2将若干工件置入一个集合中,之后C1和C2继承集合中的工件在父代的位置和值,并且将父代P1的剩余部分按照原顺序置入C2,将父代P2的剩余部分按照原顺序置入C1. 图2 POX交叉过程Fig.2 Pox crossover process 2) 关于编码中的机器部分交叉如果采用POX由于部分机器无法加工某道工序(见表1)可能导致出现不可行解,传统差分进化算法虽然在这方面设计了一种交叉方式,但是这种交叉方式得到的子代机器部分的信息继承有着一定的缺陷.因此本文在传统差分进化算法中的机器交叉的基础上进行一定的改进,操作流程如下. 以常见的一种传统交叉进化算法中机器部分交叉方法为例,首先遍历每个机器位置,例如遍历到机器位置1,生成随机数,如果随机数小于等于F,将X1的机器位置1的值赋到子代机器位置1上,否则,将X2的机器位置1的值赋到子代机器位置1上,对子代的每个机器位置操作都类似.考虑到X1和X2的机器部分的编码都是合理的,因此不会产生不可行解,但是这样的交叉方式存在一定的问题,子代基因的继承是从X1和X2轮番按位继承,优秀段的信息可能无法继承,除非连续产生的随机数都小于交叉因子,否则子代继承的基因很可能就是X1的小片段,然后是X2的小片段,之后又是X1的小片段,这样的处理仅能增加新个体的多样性,子代的质量却无从保证. 因此本节在传统差分进化算法机器交叉后得到的子代的基础上再添加一个处理方案,即对子代的机器位置再进行一次循环遍历,设定机器位置的变异因子,为每个机器位置设计一种机器选择策略,提高了差分得到的向量的质量,一定程度上改进了差分进化算法,具体操作流程如下. ① 设定机器变异因子Mr,循环遍历子代个体的机器编码. ② 遍历机器位置h时,h≥2,生成随机数,如果随机数小于Mr,对该位置进行变异,变异时统计之前各位置机器k出现的数量Mk,该位置变异取决于之前位置各机器的累计数量.例如遍历到某位置,此时生成随机数小于变异因子Mr,则变异时选择该位置为某机器k的概率为 (17) 步骤4将变异个体和父代个体X3,进行交叉 (18) 差分操作同步骤3,差分操作后得到试验个体U. 步骤5将试验个体U与当前种群中某个体进行比较,如果该试验个体的适应度较好则将该个体暂存至临时种群中,待此次迭代完成后,采用轮盘赌方法从最终种群挑取和最初种群个体数量一致的个体进入下一轮迭代[4]. 步骤6i++,判断i是否满足最大迭代次数要求,否跳到步骤3,是则退出程序,最优个体从此时的种群选出. 本节提出了一种结合模型多目标特点的初始化方法,包括工序初始化方法和机器初始化方法,其中机器初始化方面结合模型多目标特点,设定多权值综合考虑多目标进行机器初始化.并且提出一种机器选择策略用于改进差分进化算法,即在满足设定的机器变异条件时,如何对传统差分进化算法得到的子代个体的机器部分进行一次优化.下面就改进差分进化算法与传统差分进化算法进行算例验证. 为验证算法的实用性,对某加工厂的5类工件进行批量调度,5类工件的数量分别为33、45、36、60、26,根据式(15),求得等分批的最好方案为类1工件等分3批, 类2工件等分3批, 类3工件等分3批, 类4工件等分4批, 类5工件等分2批,将每个子批视为一个工件进行调度,因此共有3+3+3+4+2=15个工件,每工件4道工序,共60道工序.每类工件的单件加工信息见表1,表中52-10.13表示加工时长和能耗,其中52表示加工时长为 52 min,能耗为10.13 kW·h.考虑序列的准备时间表如表2所示. 表2 考虑上一道工序的准备时间 为验证算法的性能,在CPU型号为Intel(R) Core(TM) i5-9300H CPU @ 2.40 GHz、计算机内存为8 GB的笔记本电脑上以3.7.0版本的Python语言进行算法测试.在参数选择上,考虑到变异因子F过大会导致算法的收敛速度变慢,而过小会导致种群的多样性降低,出现早熟,因此选择变异因子F=0.5.交叉因子Cr越大交叉概率就越大,一般选择Cr=0.1.机器变异因子不宜太大,否则减缓收敛速度,本文中Mr=0.05.对比迭代次数为500、700和1 000次时,种群最优个体的适应度函数值收敛情况,如图3所示,分别代表迭代次数为500、700和1 000次时,最优个体的适应度函数值的收敛情况.通过观察可以发现迭代次数为500时,3张图收敛效果较好,超过500次后,700次迭代图和1 000次迭代图的继续收敛的程度不明显,因此取迭代次数为500进行算法对比. 图3 500、700、1 000次迭代最优个体适应度值变化曲线Fig.3 Variation curve of optimal individual fitness value for 500, 700 and 1 000 iterations 综上所述,本文以最大迭代次数500次,变异因子F=0.5,交叉因子Cr=0.1,机器变异因子Mr=0.05,种群个体数量为50作为算法参数.将改进差分进化算法对算例的调度结果和传统差分进化算法对算例的调度结果进行对比.表3为5组实验下,传统差分进化算法调度求解的各目标的调度结果,表4为5组实验下,改进差分进化算法调度求解的各目标的调度结果.从整体效果上来看,改进差分进化算法求解耗时平均为81.01 s,超过传统差分进化算法6 s,6 s的运行时间增加主要来自于初始化策略和机器选择策略的引入.但是优化后差分进化算法调度求解所得的最优个体最大完工时间、能耗、刀具磨损件数较传统算法分别优化了11.64%、14.93%和3件,极大地优化了最大完工时长、能耗和刀具磨损这3个目标. 表3 传统差分进化算法调度结果 表4 改进差分进化算法调度结果 图4(a)为传统差分进化算法500次迭代过程最优个体最大完工时间,图4(b)为改进差分进化算法500次迭代过程最优个体最大完工时间.通过对比传统差分进化算法和改进的差分进化算法的500次迭代种群中最优个体的情况,可发现在初始迭代时,改进的差分进化算法所得种群中最优个体的适应度值较低.5组实验中,改进差分进化算法初始化时所得最优个体的最大完工时间5组实验均值较传统差分进化算法初始化时所得最优个体的最大完工时间5组实验均值低100 min左右,且达到500次迭代次数时,改进差分进化算法所得最优个体最大完工时间的收敛也低于传统差分进化算法所得最优个体300 min.这表明初始化策略在算法收敛上有较为明显的作用. 图4 500次迭代过程中最优个体最大完工时间Fig.4 Maximum completion time of the optimal individual in 500 iterations 图5是在采取机器选择策略后,改进差分进化算法能耗和机器加工时间,其中图5(a)为传统差分进化算法500次迭代过程最优个体能耗图,图5(b)为改进差分进化算法500次迭代过程最优个体能耗图.可以发现,未采用机器选择策略的传统差分进化算法其最优个体能耗图各组之间上下限区间较大,震荡性较为明显,而改进差分进化算法收敛较为平滑,各组之间上下限区间较小,达到500次迭代时能耗小于传统差分进化算法,优化值为500 kW·h,一定程度上表明初始化策略在本调度模型的有效性. 图5 500次迭代过程中最优个体能耗Fig.5 Optimal individual energy consumption in 500 iterations 图6(a)为传统差分进化算法所得最优个体设备累计加工时间,从左到右,设备累计加工时间(单位:min)为3 107、4 102、3 212、4 034、3 783、3 751.图6(b)为改进差分进化算法所得最优个体设备累计加工时间,从左到右,设备累计加工时间(单位:min)为3 223、3 362、3 342、2 994、3 201、3 402.同样可以发现传统差分进化算法进行机器部分编码的交叉时只是单纯地增加机器编码的全局性而未考虑机器编码部分的质量,极易出现负载不均的现象,而考虑机器选择策略的改进差分进化算法的设备工作时间较为均衡. 图6 最优个体设备累计加工时间Fig.6 Cumulative processing time of optimal individual equipment 最终获得一个可用的调度结果染色体:[工序部分:1 5 2 3 13 1 7 14 5 6 11 4 12 15 9 5 7 2 4 14 5 1 15 12 8 3 13 1 10 11 12 4 12 3 9 11 10 8 10 3 9 11 8 14 13 6 14 15 4 6 7 10 9 8 2 2 7 15 6 13;机器部分:6 4 2 4 5 2 1 4 5 4 1 5 2 3 4 4 2 1 1 6 5 2 4 2 4 4 4 3 2 5 1 3 4 6 3 3 2 5 1 3 6 3 6 5 1 3 6 3 5 2 4 6 3 1 3 6 2 5 3 1]. 其调度甘特图如图7所示,其最大完工时间为3 511 min,能耗为8 640 kW·h,预估损坏刀数30把. 图7 最优调度方案Fig.7 Optimal scheduling scheme 本文针对机加工柔性作业车间工件品种和批量较多、车间环境较为复杂导致的调度成本过高、机器设备负载不均衡的问题进行研究,取得了以下结论. 1) 以最大完工时间、能耗和刀具损耗数量为优化目标,以返工、批量调度和考虑序列的准备时间作为约束建立了多目标机加工柔性作业车间调度模型,该模型能有效反映实际多目标机加工柔性作业车间生产特点. 2) 设计一种改进差分进化算法,通过实际算例测试,分别分析改进差分进化算法和传统差分进化算法对多目标机加工柔性作业车间调度模型求解结果,发现基于改进差分进化算法的多目标机加工柔性作业车间调度结果较优,有一定的实用价值.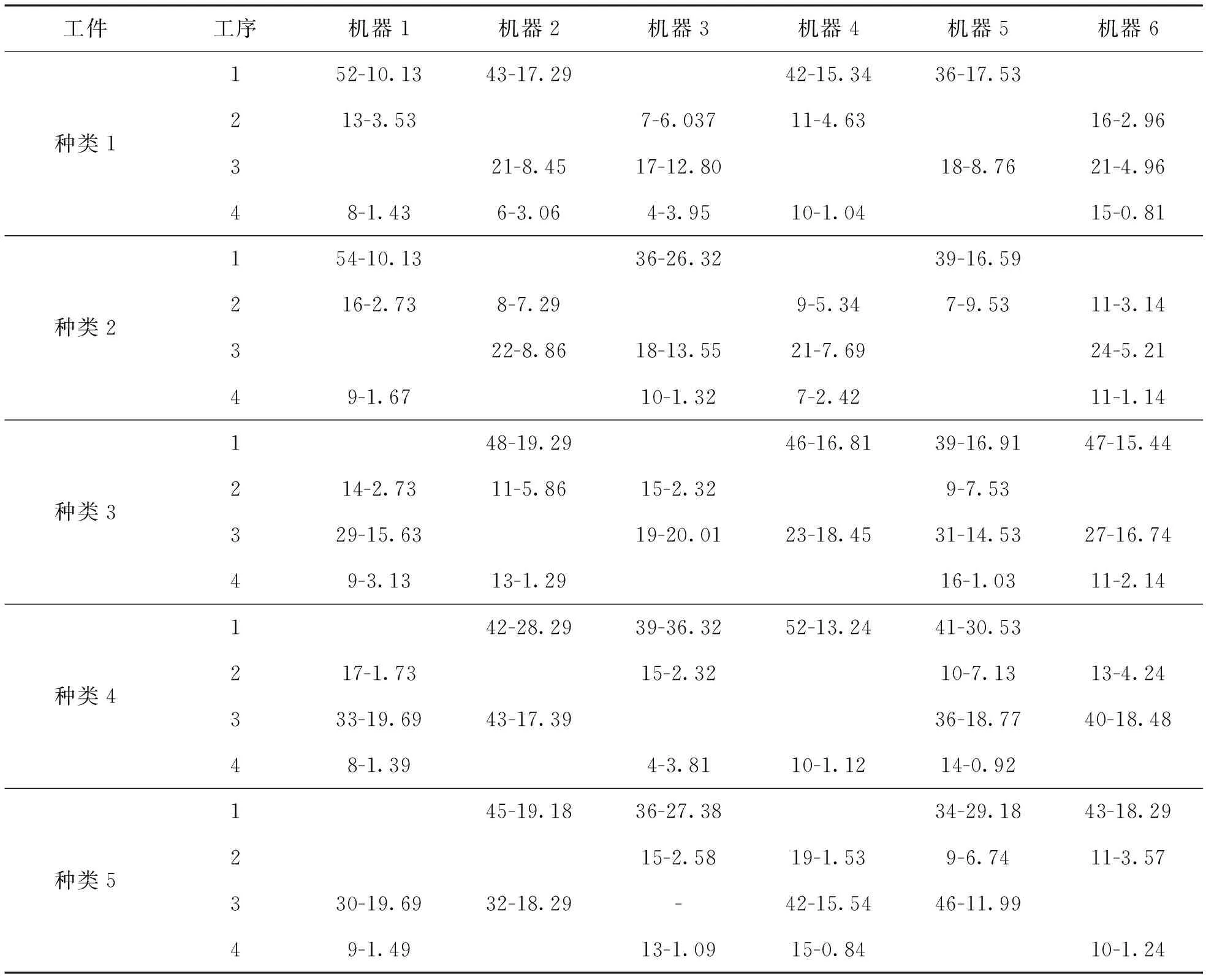
2.2 多目标适应度函数设计
2.3 初始化种群
2.4 差分进化



2.5 小结
3 算例验证分析







4 结论
