基于支持向量机和灰色BP神经网络的冬小麦晚霜冻害预测

时 雷，孙佳佳，孙嘉玥，郭三党，郑 光，席 磊，张娟娟

(1.河南农业大学信息与管理科学学院，河南郑州 450046；2.农田环境监测与控制技术河南省工程实验室，河南郑州 450046；3.河南粮食作物协同创新中心，河南郑州 450046)

晚霜冻害是一种短时间突发性的低温农业气象灾害，是黄淮海平原春季常见的气象灾害之一，冬小麦受其影响较深。晚霜冻严重影响冬小麦幼穗分化进程时可造成60%以上的减产，使冬小麦生产遭受巨大损失[1]。受全球气候变化和极端气象频发的影响，淮河流域终霜日提前[2]，冬小麦的物候期提前，拔节孕穗期抗寒能力衰减[3]，晚霜冻害的发生趋于频繁，危害趋于严重，因此，准确地对晚霜冻害进行预测意义重大。

近年来，“3S”技术[1]和各种预测模型[4-6]被广泛应用于晚霜冻害的监测和预警中。其中，预测模型有灰色预测模型[7-8]、回归预测模型[9-10]、神经网络模型[11-12]、支持向量机模型[13]和马尔可夫模型[14]等[15]。晚霜冻害发生的规律性不强，因此其数据收集难度较大。使用传统的数据统计、时间序列分析和线性回归方法虽然简单易实现，但是其对数据的完整性和连续性要求较高，且预测结果精度一般。灰色预测模型[16]的数据可以是“贫信息和小样本”[17]，对于噪声数据、少信息数据更具有鲁棒性，具有计算过程简便、预测精度高的优点[18]。使用GM(1，1)模型对霜冻特征值超过设定阈值的异常值出现时期进行预测，以实现晚霜冻的灾变预测。

灰色BP神经网络是灰色模型和BP神经网络模型的结合，实现了2个模型的优势互补，在农业的产量预测、灾害预测上都有良好应用。Li等使用灰色BP神经网络分别预测河南省的灾害发生和粮食产量，取得良好结果[19-20]；王安等针对产量预测问题研究单变量预测模型中灰色神经网络模型的应用情况，证明在单变量预测模型中灰色神经网络模型比GM(1，1)、恩格尔GM(1，1)和离散GM(1，1)模型预测结果更好[21]。灰色预测模型和神经网络模型的结合方式也逐渐多元化，对灰色模型的预测结果进行残差修正不仅效果好而且易实现。支持向量机因擅长预测不规则数据常被应用在残差修正问题中，耿立艳等使用支持向量机修正差分整合移动平均自回归模型预测的残差[22]；杜文然等使用支持向量回归机对改进后的GM(1，1)预测残差进行修正，模型的精度均得到显著提升[23-24]。残差修正方法被较多运用在单一模型的残差修正中，在组合模型中使用较少。

本研究基于河南省商丘市1980—2019年的终霜日数据，实现数据的预处理，筛选不同的灰色模型作为BP神经网络的输入，使用支持向量机对 GM(1，1)和离散GM(1，1)模型的预测结果进行残差修正，利用BP神经网络将残差修正后的灰色模型和等维递补离散GM(1，1)的预测结果加入神经网络上进行训练、建模，以期为实现冬小麦晚霜冻害的预测及防灾减灾提供有效的技术支持。

1 材料与方法

1.1 数据来源和终霜日定义

在霜冻灾害中，通常使用日最低气温0 ℃作为阈值，认为低于这个阈值将会引起霜冻灾害发生[25-27]。有关终霜日参照农业气象学[28-29]定义：取每年春季最后1次出现每日最低温度在0 ℃以下，记这一日为该年的终霜日。气象数据来源于中国气象数据网(http：//data.cma.cn/)，包括河南省商丘市气象站点1980—2019年3—5月的逐日最低气温数据记录。筛选每日最低温度低于0 ℃的日期数据，得到商丘1980—2019年的终霜日数据。

在全球气候变暖背景下，淮河流域气温上升速率显著[2，30]，终霜日稳定性降低[30]。冬小麦晚霜冻害的发生与终霜日期密切相关，随着冬小麦生育期进入拔节期，抗寒能力减弱，终霜日发生时间越晚，对冬小麦的生产威胁越大。冬小麦的拔节期和终霜日受不同地域影响呈现趋势变化。河南省商丘市位于114°49′～116°39′E、33°43′～34°52′N之间，其拔节期主要出现在3月9—17日[31]，所以本研究认定终霜日晚于3月17日会引起晚霜冻害。

1.2 GM(1，1)、离散GM(1，1)和等维递补离散GM(1，1)模型

1.2.1 原始灾变序列的建立和GM(1，1)模型的建立 整理后的终霜日数据，在不考虑年份的情况下按照日期先后排序，记最早的终霜日期为零点，其后各终霜日期与零点的间隔天数记为相对日期，得到1980—2019年终霜日相对日期序列。确定最早灾变日期，并以此为基准作灾变折线图，得到原始灾变序列I(0)，即

I(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}。

(1)

式中：x(0)为原始灾变数据；n为研究区域年份总计数。

对I(0)进行累加生成处理得到序列I(1)：

I(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}。

(2)

相应的微分方程为

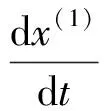
(3)

式中：a是反映系统发展态势的发展系数；b是作用量，反映数据的变化关系。

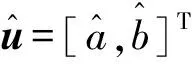
(4)

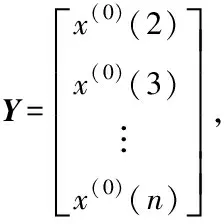
则式(3)可以表示为

Yn=Bα。

(5)

则GM(1，1)模型的时间响应函数为

(6)

1.2.2 离散GM(1，1)和等维递补离散GM(1，1)模型的建立 离散GM(1，1)模型的定义。假设I(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}为非负序列，累加生成序列为I(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}，则称：

x(1)(K+1)=β1x(1)(K)+β2。

(7)

为离散GM(1，1)模型，该模型的解为

(8)

离散GM(1，1)模型的时间响应函数为

(9)

等维递补思想在预测问题上也称为滚动式预测[32-33]，在传统灰色预测模型的过程中，利用灰色预测模型预测结果越靠后精度逐渐降低的特点，通过不断加入新信息，同时去掉旧信息，保持数据序列与原序列的数据等维，依次递补预测，实现灰色模型的动态预测，可以有效降低由于灰色预测结果随时间外推灰度逐渐上升造成的误差。等维递补离散GM(1，1)模型吸收了等维递补思想和离散 GM(1，1)模型的优点，预测精度有效提升，在试验中被证明更适用于冬小麦晚霜冻害的预测。

1.3 支持向量机残差修正模型

支持向量机回归模型[34]是用来解决小样本、非线性回归问题的算法，该算法将已知空间映射到高维空间，实现样本由非线性到线性的转变。设低维空间中的非线性样本集为{xj，yj}，其中：xj=[xj1，xj2，…，xji]为输入向量，yj为对应输出值，j为样本数，i为输出向量个数，则SVM回归模型为

f(x)=WTφ(x)+b。

(10)

式中：WT为估计函数的自变系数；φ(x)是非线性映射函数；b为偏置量。

支持向量机回归模型可以实现对残差序列的回归预测，以支持向量机为理论基础建立的回归模型在准确度上有很好的性能[35]。

1.4 BP神经网络预测模型的建立

区别于支持向量机模型，BP神经网络模型利用非线性基函数的线性组合实现从输入空间到输出空间的非线性转换[37]，在非线性问题预测上适应良好。BP神经网络是典型的3层网状结构，具体结构见图1。

输入层到隐藏层的连接权值为wij，i=1，2，…，n，j=1，2，…，隐藏层到输出层的连接权值为wjm，m=1，2，…，j=1，2，…，隐藏层阈值为bi，输出层阈值为bm。经试验，本研究设置输入层节点为3，训练函数为Sigmoid函数，隐藏层节点为8，输出层节点为1，训练函数为线性传递函数，模型的训练函数为标度共轭梯度算法。

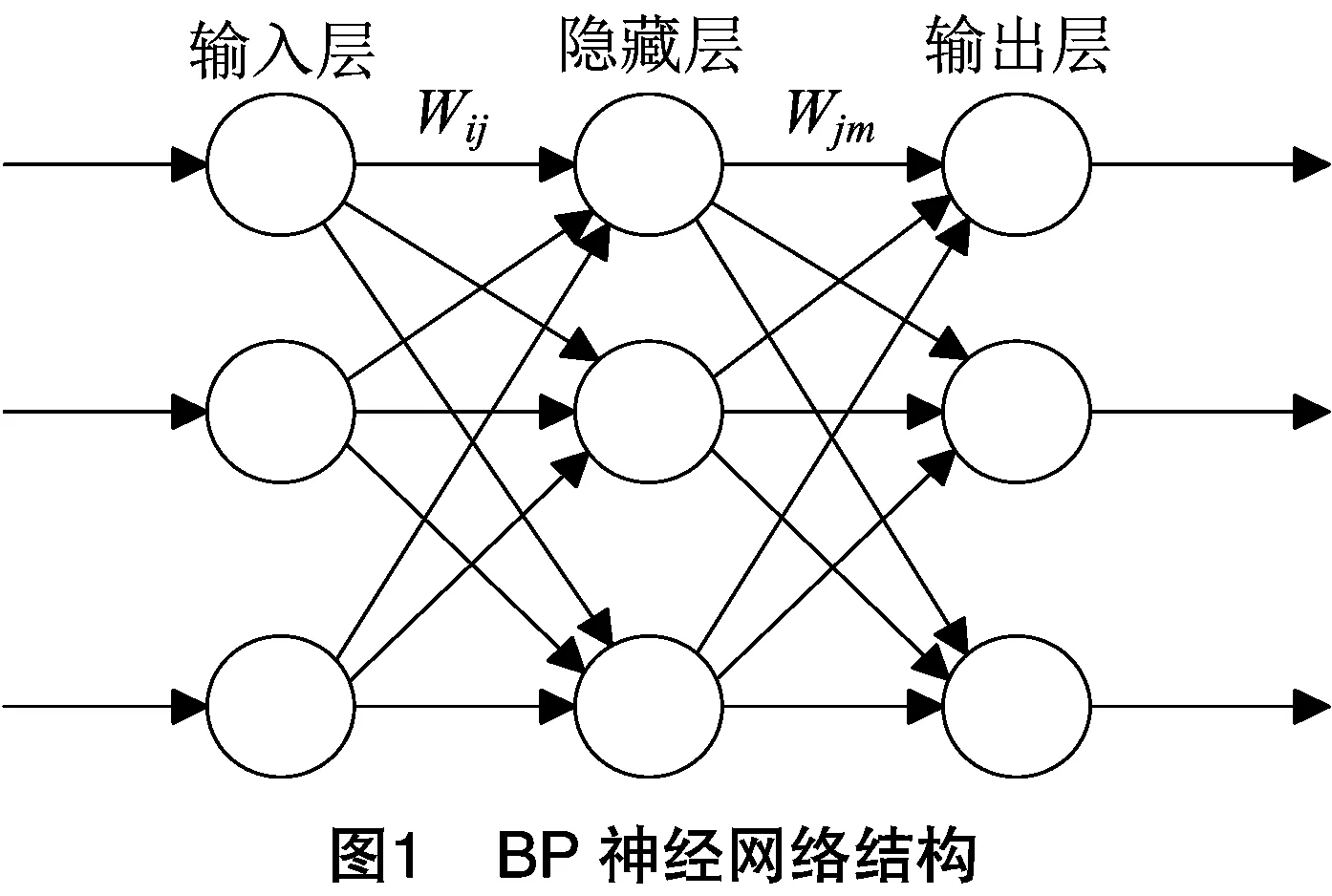
将残差修正后的GM(1，1)模型、离散GM(1，1)模型和等维递补离散GM(1，1)模型的预测结果作为BP神经网络的输入，真实值作为输出。

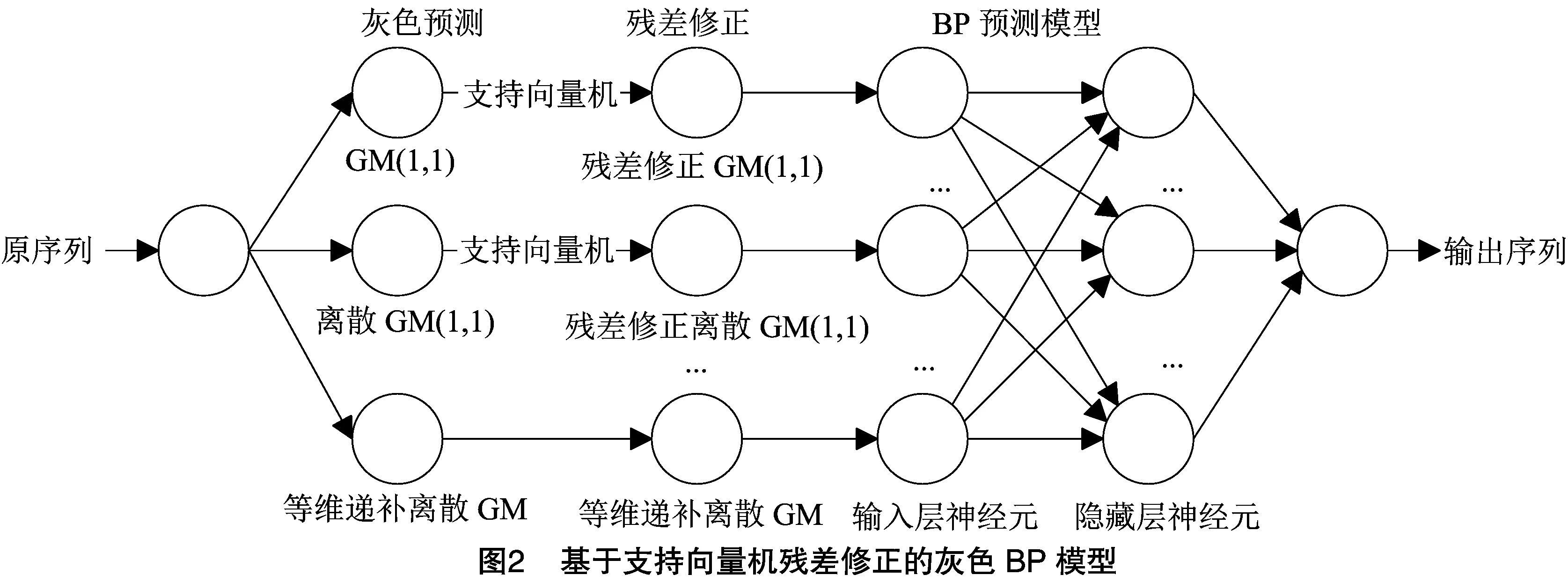
1.5 支持向量机残差修正的灰色BP模型的构建

基于支持向量机残差修正的灰色BP神经网络模型的结构见图2，建模步骤具体如下：

步骤一：将处理好的数据序列分别进行GM(1，1)、离散GM(1，1)和等维递补离散GM(1，1)模型预测。

步骤二：使用支持向量机回归模型对GM(1，1)和离散GM(1，1)的预测结果进行残差修正，分别得到残差修正后的GM(1，1)和离散GM(1，1)模型，等维递补离散GM(1，1)的预测结果不作处理。

步骤三：分别将残差修正后的GM(1，1)、离散GM(1，1)和等维递补离散GM(1，1)3个模型的预测结果输入到BP神经网络，作为输入层，将实际值放到网络的输出层，最终训练得到BP模型。

1.6 模型的检验

各个模型建立后，采用平均相对误差、平均绝对百分比误差和均方差比值对模型进行检验，精度等级的评判标准见表1。

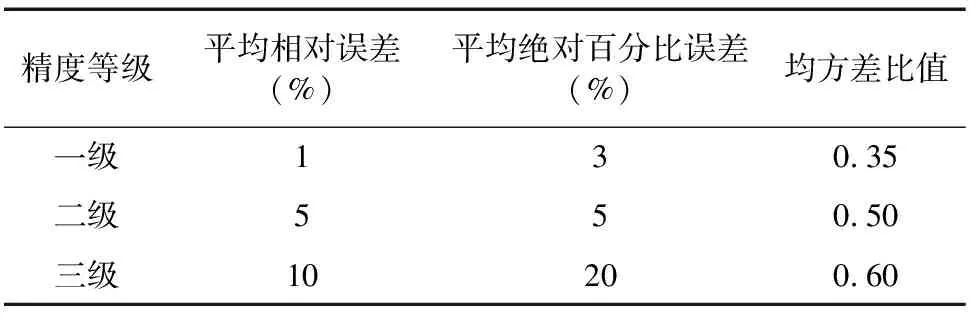
表1 精度检验等级参照

表1中平均相对误差的计算公式为

(11)

平均绝对百分比误差可以用公式表现为

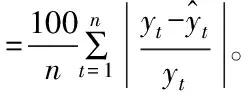
(12)

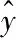
均方差比值指用残差数据序列的均方差除以原始灾变序列的均方差，即

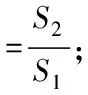
(13)

(14)

(15)

2 结果与分析

2.1 形成灾变间隔的原始序列集

对终霜日数据进行整理后可知，商丘市在1980—2019年的40年间，春季终霜日出现日期最早为3月1日，最晚为3月31日。以3月1日为0点，按照“1.2.1”节的步骤将终霜日序列转换为终霜日相对日期序列，具体结果见表2。

数据(表2)显示，商丘市1980—2019年间的终霜日均发生在3月，当终霜日发生日期晚于3月17日，会发生晚霜冻害，确定3月17日为灾变日期，记相对排序阈值为14。

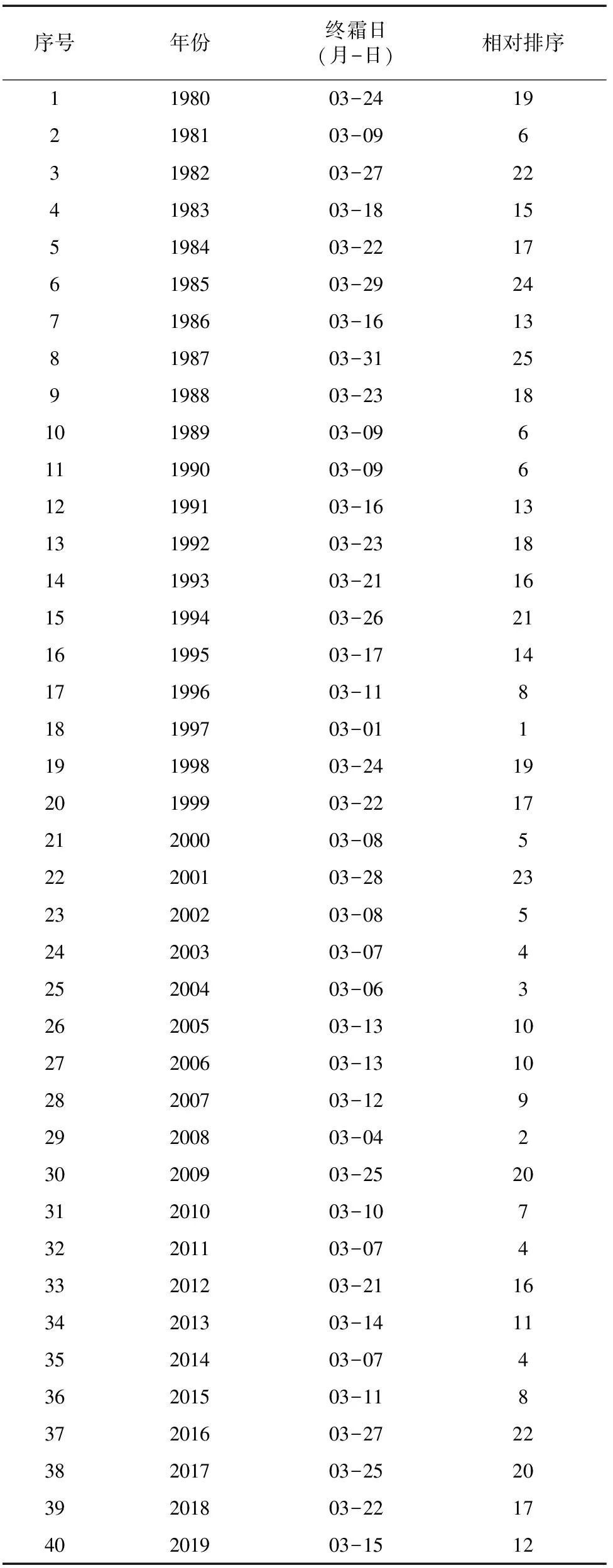
表2 商丘市1980—2019年终霜日相对排序

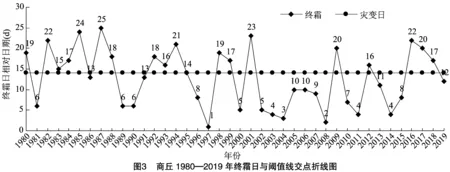
根据相对排序序列绘制折线图，加入阈值绘制等值水平线，得到商丘市1980—2019年终霜日相对排序及阈值线的交点见图3。

从图3中得到终霜日相对排序与阈值线的交点集，共计17个交点。取第1个交点为0点，计算其余16个交点到0点的距离。由于交点并不统一落入整数点，将横坐标的1个单位再进行10等分，最终记录16个间隔数据，得到商丘晚霜冻害发生间隔柱状图(图4)。

由相对距离数据建立原始灾变间隔时间序列集，即

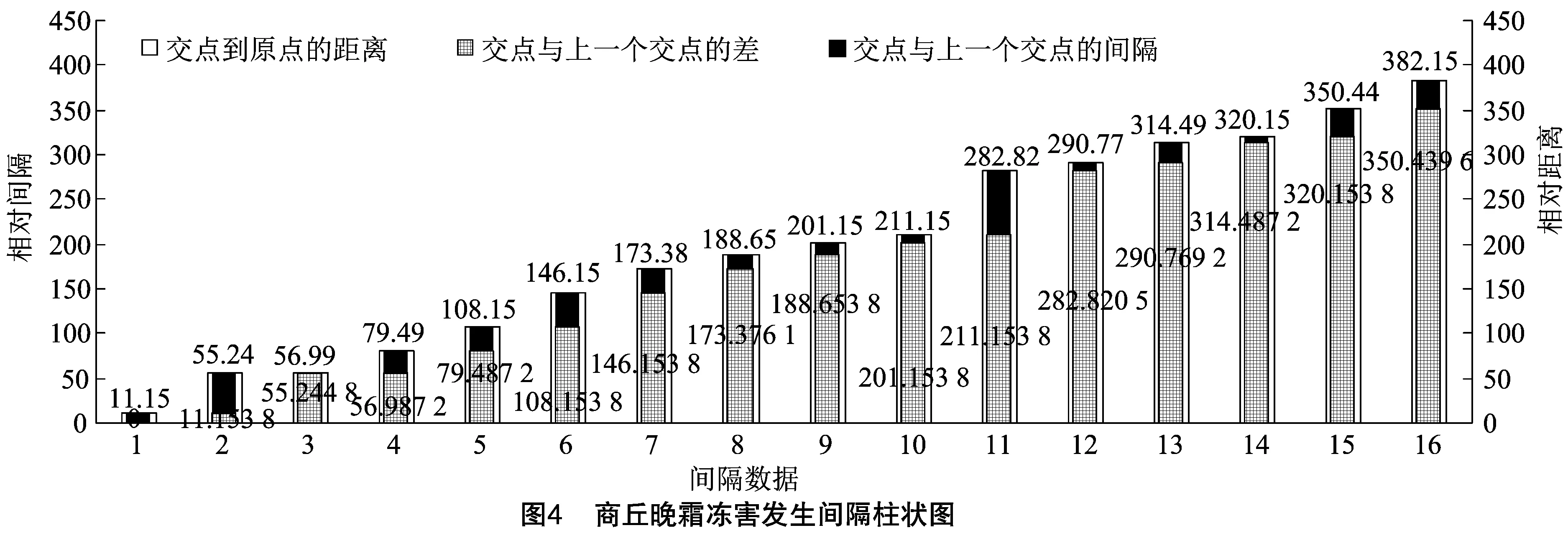
I(0)={x(0)(1)，x(0)(2)，…，x(0)(16)}。

(16)

2.2 数据的检验和处理

当数据序列呈现指数增长时，在灰色模型中应用良好。为保证模型的预测准确性，需要对数据进行必要的检验处理。对原始数据I(0)进行级比检验：

(1)求级比λ(t)。

(17)

λ=[λ(2)，λ(3)，…，λ(16)]=(0.201 9，0.969 4，0.716 9，0.734 9，0.740 0，0.843 0，0.919 0，0.937 9，0.952 6，0.746 6，0.972 7，0.924 6，0.982 3，0.913 6，0.917 0)。

(18)

(19)

(3)平移变换处理。取适当的常数c=363，对I(0)(t=1，2，…，16)进行平移变换处理：

y(0)(t)=x(0)(t)+c，t=1，2，…，n-1。

(20)

得到：

y(0)={x(0)(1)，x(0)(2)，…，x(0)(16)}=(374.153 8，418.244 8，419.987 2，442.487 2，471.153 8，509.153 8，536.376 1，551.653 8，564.153 8，574.153 8，645.820 5，653.769 2，677.487 2，683.153 8，713.439 6，745.153 8)。

(21)

得到相应的级别值为

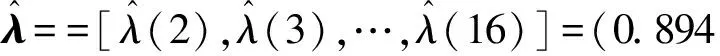
(22)

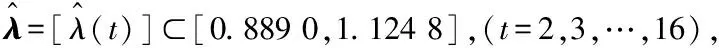
在试验过程中，选取序列的前11位作为试验数据，后5位数据作为试验的真实值。

2.3 试验过程

2.3.1 分别建立灰色模型 对序列y(0)进行以此累加得到：

y(1)={x(1)(1)，x(1)(2)，…，x(1)(11)={374.153 8，792.398 6，1 212.385 8，1 654.873 0，2 126.026 8，2 635.180 6，3 171.556 7，3 723.210 5，4 287.364 3，4 861.518 1，5 507.338 6}。

(23)

GM(1，1)建模后得到发展系数a=-0.047 4，灰色作用量b=383.500 4，相应的白化解为：

(24)

根据等维递补思想，依次递补预测，得到等维递补的GM(1，1)模型的5步预测值。

离散GM(1，1)建模后得到β1=1.048 5，β2=392.909 7，相应的白化解为：

根据等维递补思想，逐步获得5个预测值。

经过以上4个灰色模型预测过程，得到 GM(1，1)、离散GM(1，1)、等维递补GM(1，1)和等维递补离散GM(1，1)模型的预测结果(表4)。

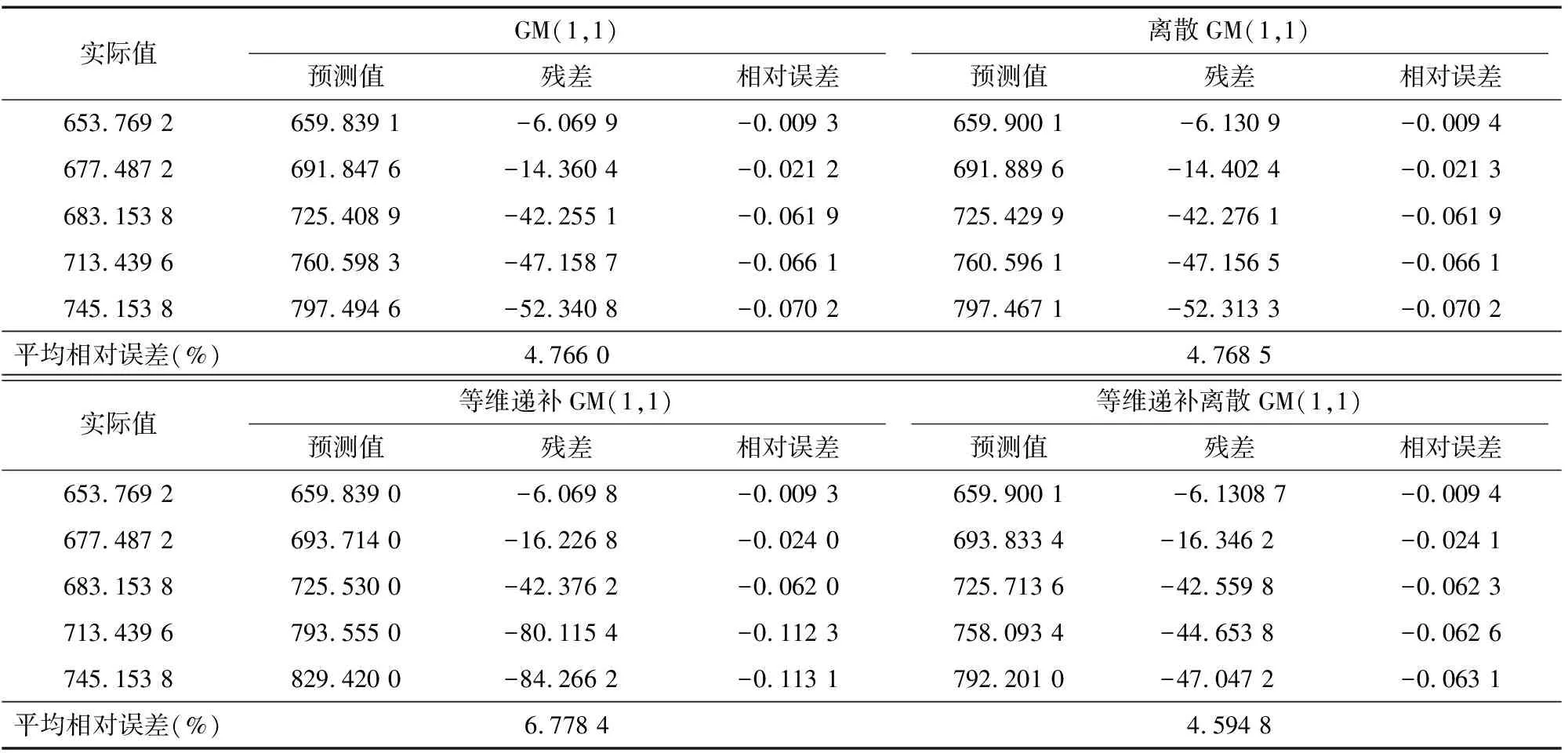
表4 灰色模型的预测值及误差

使用平均相对误差对以上4种灰色模型进行评价，发现GM(1，1)、离散GM(1，1)和等维递补离散GM(1，1)模型的预测精度较高，平均相对误差较低，其中等维递补离散GM(1，1)模型的预测精度最高；等维递补GM(1，1)模型的预测精度下降，平均相对误差和残差数值较大。因此，选择GM(1，1)、离散GM(1，1)和等维递补离散GM(1，1)模型的5步预测结果作为灰色BP神经网络的输入。

2.3.2 使用支持向量机回归模型分别对GM(1，1)和离散GM(1，1)的预测结果进行残差修正 根据灰色模型的白化方程可以得到序列y(0)前11位的模拟值z0={x(0)(1)，x(0)(2)，…，x(0)(11)}和后5位预测值z0={x(0)(12)，x(0)(13)，…，x(0)(16)}，将它们和y(0)={x(0)(1)，x(0)(2)，…，x(0)(16)}对应作差，得到对应的残差序列：

δ0={x(0)(1)，x(0)(2)，…，x(0)(11)}；δ0={x(0)(12)，x(0)(13)，…，x(0)(16)}。

(25)

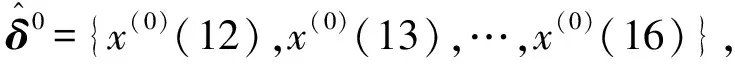
对残差修正前后的灰色模型预测结果进行评价，结果见表5。由表5可知，相较原始的GM(1，1)和离散 GM(1，1)模型，残差修正后的灰色模型精度提升明显，其中残差修正后的GM(1，1)模型预测结果最佳，其方差比达到一级，平均相对误差、平均绝对误差均达到二级标准。

表5 支持向量机残差修正前后灰色模型预测结果评价

2.3.3 对残差修正后的灰色预测结果进行BP神经网络预测 经过支持向量机模型残差修正后得到等维递补离散GM(1，1)、残差修正GM(1，1)和残差修正离散GM(1，1)模型的5步预测结果见表6。

表6 灰色模型的预测结果

将以上数据作为BP神经网络的3个输入，真实值作为BP神经网络的输出，进行BP神经网络建模，相关参数参考“1.4”节，得到灰色模型和基于支持向量机残差修正后的灰色BP神经网络模型的预测结果对比(图5)。

由图5可知，本研究提出的支持向量机残差修正的灰色BP神经网络模型的预测结果与真实值最接近，模型的预测性能更好。

2.4 模型检验结果

2.4.1 对比模型预测 为了更客观全面对模型精度进行检验，本研究将滚动式BP神经网络预测模型、原始差分GM(1，1)预测模型和均值差分 GM(1，1)预测模型加入预测结果精度检验。滚动式BP神经网络预测模型是在40年终霜日灾变间隔序列数据的基础上进行滚动式处理，将前4步数据作为输入、第5步数据作为输出，从而建立BP神经网络模型。差分GM(1，1)预测模型是GM(1，1)模型的一种经典改进模型，其在灰色模型中引入了差分模型，最终得到对比模型的预测结果(表7)。

表7 对比模型的5步预测结果

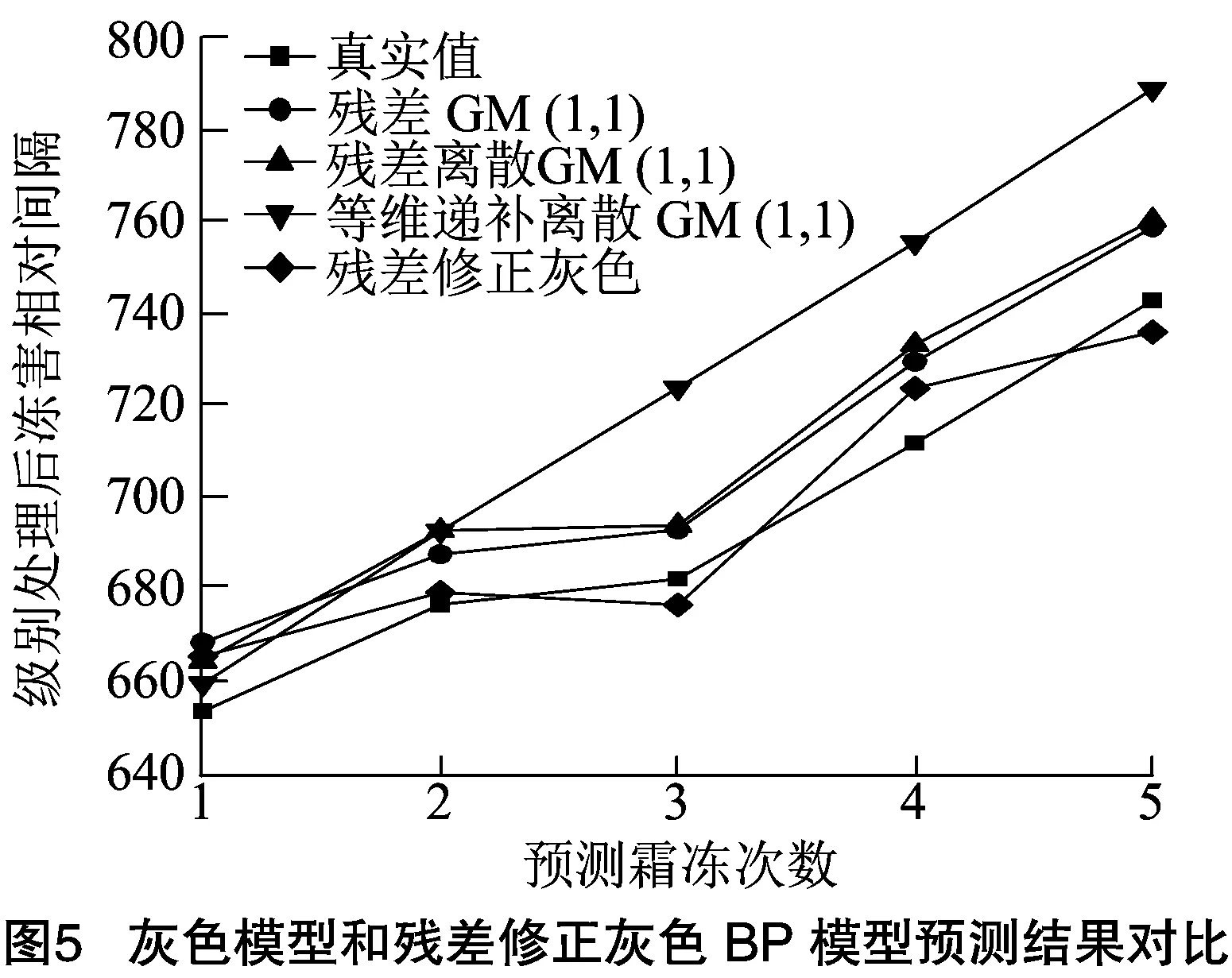
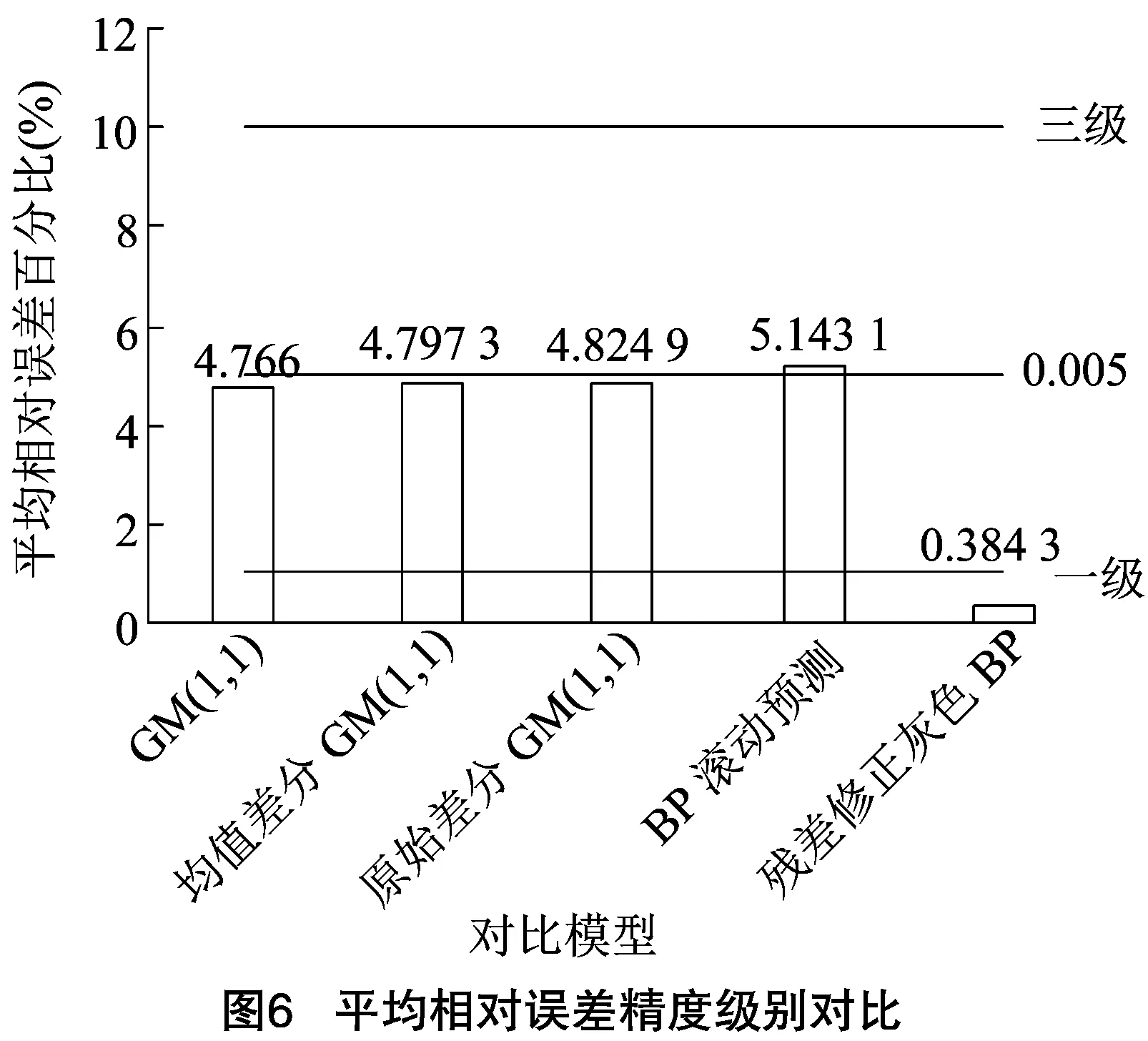
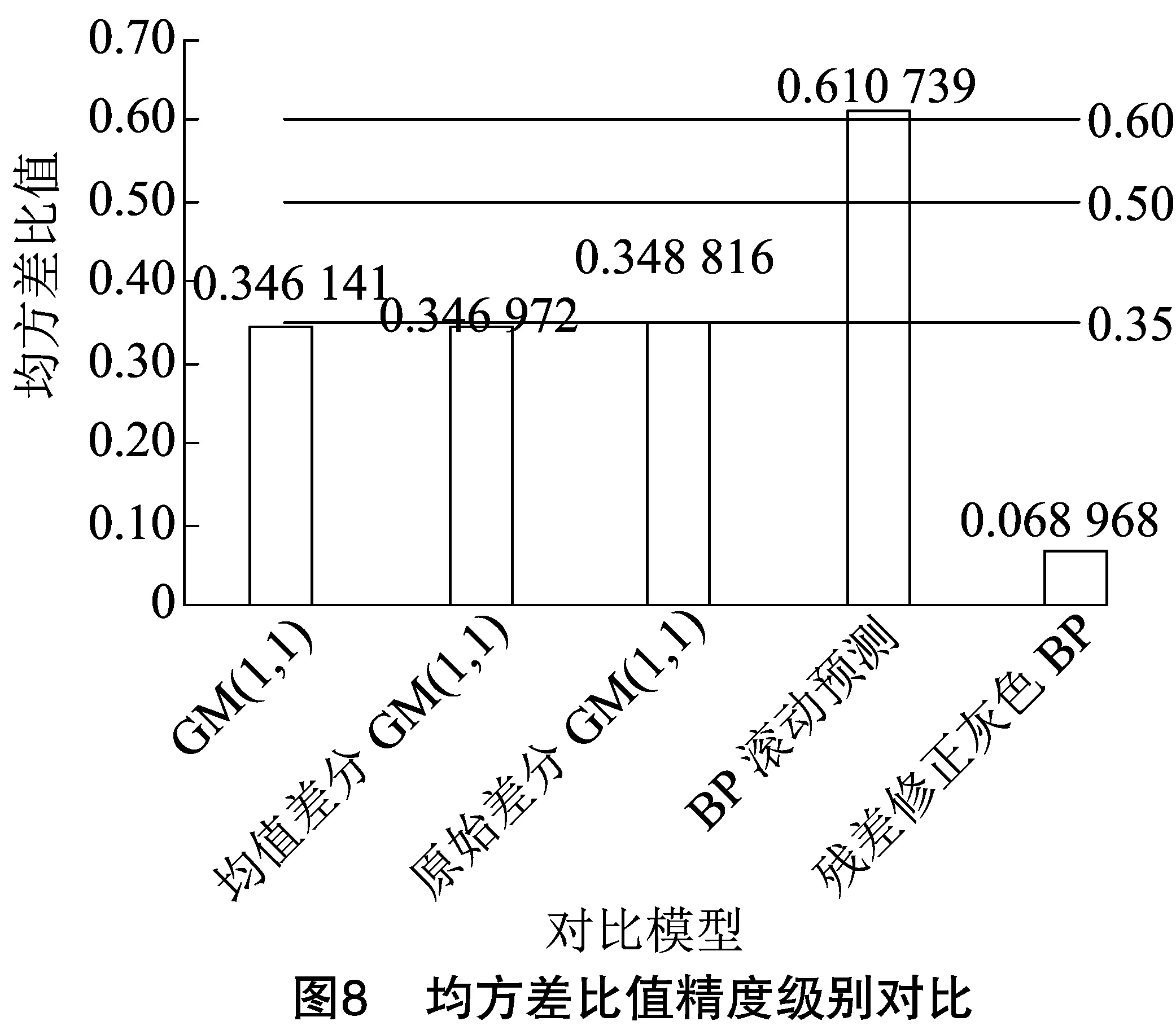
2.4.2 对模型的预测结果进行误差评价 根据表1的精度检验等级对模型的结果进行分级对比，分别从平均相对误差、平均绝对百分比误差和均方差比值3个方面对模型的结果进行分析，分别得到精度级别对比结果(图6至图8)。

由图6可知，使用单一数据进行滚动式BP神经网络预测精度较差，平均相对误差精度等级达到三级；灰色模型包含GM(1，1)、原始差分GM(1，1)和均值差分GM(1，1)的平均相对误差精度均处于二级，结果较为稳定；本研究提出的模型基于支持向量机残差修正的灰色BP神经网络模型的平均相对误差精度达到一级标准。

由图7可知，滚动式BP神经网络预测精度最低，处于三级；灰色模型精度比较接近，均为二级，本研究提出的模型精度较高，平均绝对百分比误差达到一级精度。

由图8可知，滚动式BP神经网络模型的预测结果最差，远低于图中其他模型；几个灰色模型的均方差比值刚达到一级，本研究提出模型的均方差比值高于一级，结果比灰色模型的预测结果更好。

2.5 利用本研究提出残差修正的灰色神经网络模型对商丘灾变年份进行预测

由以上分析可知，经过支持向量机残差修正后的灰色BP模型的预测结果性能最优，且符合精度标准要求，可以用来预测晚霜冻。在实际的应用过程中，考虑到模型预测值的实际意义为霜冻发生年份的间隔，需要对数据进行预处理和还原过程。

分别将级别处理后的第12步到第16步数据放入经支持向量机残差修正的灰色BP神经网络模型中，得到预测结果(表8)。

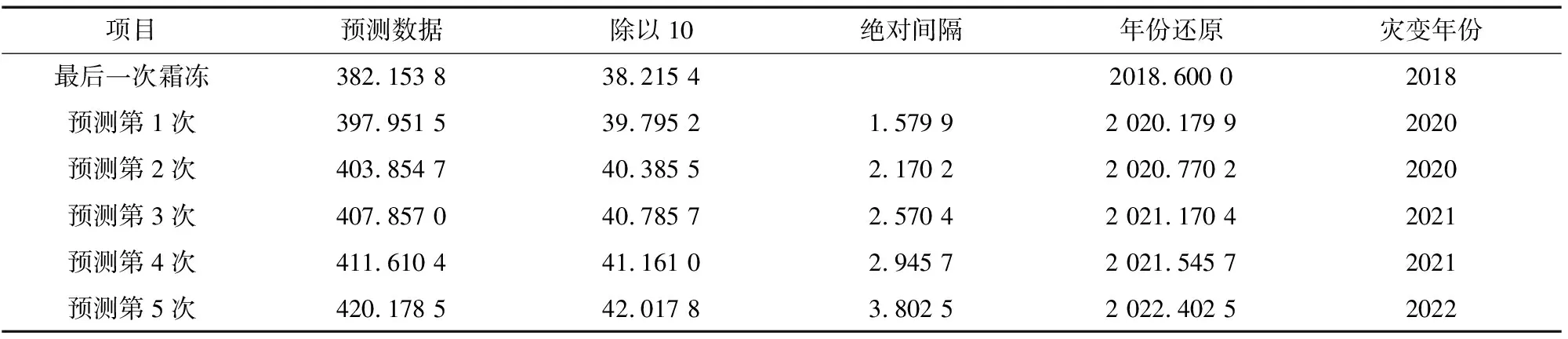
表8 霜冻预测年份还原表

由图4可知，商丘最后一次发生晚霜冻的时间为2018年，经过预测后本研究预测未来发生霜冻的年份为2020、2021、2022年，得到商丘1980年以来的晚霜冻灾害年份分布(图9)。

根据商丘气象站公布的数据，2020年商丘终霜日为3月30日，3月26—28日商丘全市出现寒潮大风降温天气，大部分地区出现晚霜冻，与本研究模型预测结果相符。2021年商丘各市区终霜日出现日期均为4月4日，较往年较晚，远超本研究设定的灾变阈值3月17日，符合本研究预测结果。

对图9进行分析。发现未来晚霜冻发生年份规律与1999—2001年的灾害发生情况相似，均为连续发生，相邻10年晚霜冻灾害发生频率约为2～4年出现1次。根据这个规律，本研究认为2022年后晚霜冻发生的频率会降低到2～4年1次。

3 结论

为提高冬小麦晚霜冻害预测的准确性，本研究提出了一种基于支持向量机残差修正的灰色BP神经网络模型，该模型在符合自身数据特点的基础上结合神经网络模型、支持向量机模型和等维递补思想等模型优化方法，有效提升了灰色模型的预测精度。在河南省商丘气象站1980—2019年的终霜日数据上的试验表明：使用支持向量机残差修正后的灰色BP神经网络模型可以实现冬小麦晚霜冻的预测，根据本模型预测结果，2020、2021年会发生晚霜冻，与当地气象站公布数据相符，未来预测2022年有可能出现霜冻。

本研究在宏观方面实现了冬小麦晚霜冻害的灾变年份预测，未来可以考虑加入更多影响因素，构建多维的灰色BP神经网络模型，以实现对冬小麦晚霜冻害更加精确、全面的预测。