盾构滚刀作用下混凝土材料破碎分形与能耗

2023-03-16岳玮琦顾展飞苏伟林

材料科学与工程学报 2023年6期

岳玮琦,顾展飞,苏伟林

(1.郑州航空工业管理学院土木建筑学院, 河南郑州 450046; 2.黄河勘察规划设计研究院有限公司, 河南郑州 450003; 3.北京交通大学土木建筑工程学院, 北京 100044)

1 前言

盾构技术的发展为城市地铁隧道掘进提供了安全、高效、环保的施工方法,然而近年来部分城市可供利用的地下空间日趋饱和,盾构掘进面临愈发复杂的施工环境和层出不穷的障碍限制。密集的房屋、桥梁等已建构筑物所附属的地下桩基、连续墙等混凝土结构常常成为盾构掘进路线上的重大障碍[1-4],导致盾构机需要直接切削破除此类障碍物;除此之外,盾构机在始发和接收时还需要直接破除混凝土封门。盾构破除地下混凝土结构施工极大威胁着上部结构的安全,同时,刀盘和刀具也容易因承受较大的荷载而发生损坏,由此造成盾构掘进缓慢甚至停滞,会进一步增大此类施工的风险。同时,不当的掘进参数还会导致刀盘能耗急剧增大,为刀盘功率的匹配带来挑战。

为了顺利破除混凝土障碍,拓展盾构法适用范围,并最大程度减少破除施工对刀盘刀具的损害,广大学者和从业人员开展了一系列关于盾构破除混凝土材料的研究工作,取得了丰富的研究成果。袁大军等[5]依托实际切桩工程开展了现场盾构刀具切桩试验,并且研发了新型贝壳刀,认为切削混凝土机理为挤压损伤;王哲等[6]根据柔软黏土地层中桩基特点开展了刀具选型研究,同时采用有限元软件对撕裂刀形状进行设计,发现采用其刀具形状结合高差立体刀具布置切削桩基效果较好;王飞等[7]开展盾构直接切削直径1 200 mm 桩基的现场试验,分析了切桩效果与刀具损伤规律,提出了合理的刀具配置方案与掘进参数;苏伟林等[8]结合混凝土试块切削试验,研究了HJC混凝土动本构模型参数的设置方法,并据此对混凝土在盾构刀具作用下的破坏进行数值计算。然而,目前对滚刀作用下混凝土的破碎效果缺乏有效的衡量指标,对单把刀具的破碎能耗也缺乏有效的监测手段,从而造成盾构破除施工的参数选择往往具有较大的盲目性。

分形理论自被Mandelbrot[9]提出之后,在水泥基材料的强度、抗裂性、压缩破碎特征等材料性能的评价和改善方面得到了广泛应用。吴剑锋等[10-11]的研究揭示了混凝土在单轴受压破碎后的碎屑分形特征随着粗骨料粒径的增大而减小、同时随着混凝土单轴抗压强度的增强而增大的规律。他们还根据峰值抗压强度和残余抗压强度计算了混凝土的脆性指标,并探讨了粗骨料粒径和试样形状对这一指标的影响。此外,他们还深入分析了抗压强度、峰值应变、单位体积吸收能、破碎分形维数与脆性指标之间的关系;李丽明等[12]建立了沥青混凝土抗车辙性能与级配粒径分形维数之间的联系,提出了一种有效的预控方法,用于改善骨架密实型沥青混合料的抗车辙性能;赵昕等[13]利用Hopkinson压杆对混杂纤维UHTCC材料进行了不同温度下的动态压缩试验。他们收集了冲击破碎后的试块,并对其分形特征进行了分析。结果显示,UHTCC材料的分形维数随温度的升高而降低;王芬奇等[14]利用Hopkinson压杆试验系统与含水率控制法,分析了不同含水率混凝土试样的动态力学参数变化特征,通过引入块度分析法和分形理论,探讨了动荷载作用下混凝土试样的破坏特征随含水率的变化规律;Volchuk等[15]提出了使用分形理论测试混凝土断裂应力的方法,并设定了混凝土断裂应力和分形测量值之间的关系,将分形维数用于预测混凝土性能及结构变化指标;Gao等[16]引入分形维数作为一个综合指标,描述再生骨料的复杂性质及其对再生混凝土性能的影响,研究发现,颗粒群状态下再生骨料的容重、吸水率和破碎指数的顺序与边界线的分形维数有明显的直接关系。

本研究从混凝土材料在盾构滚刀作用下破碎后的自相似性出发,探究了不同强度混凝土在不同盾构掘进参数下的破碎分形特征,据此得到滚刀破除不同强度混凝土时的能耗计算方法,为临时支护结构混凝土强度的选择、盾构破除时掘进参数的设定以及所需匹配的刀盘功率与能耗评估提供一定的理论依据。

2 混凝土破碎分形

混凝土是一种多相人工复合材料,内部随机分布着大量的孔隙、裂纹等损伤结构,其分布规律满足一定的统计自相似性,混凝土材料在外部荷载作用下发生破碎时往往从内部损伤部位发生破坏,因而形成的混凝土碎屑也会表现出较为明显的分形特征[17-20]。

2.1 分形维数计算

根据分形理论,混凝土碎屑经组合筛筛分后,筛孔直径与筛下碎屑体积满足以下关系[21]：

V2=Vv[1-(di/dv)3-D]

(1)

式中：V2为筛分时通过直径为di的筛孔的混凝土碎屑总体积;dv为碎屑颗粒最大直径;VV为混凝土碎屑总体积;D为分形维数。为了便于统计,认为混凝土材料的平均密度为ρ,将式(1)换算成质量关系：

M2=ρV2=ρVv[1-(di/dv)3-D]

(2)

M=ρVv

(3)

式中：M为混凝土碎屑总重量。根据式(2)、(3),混凝土碎屑的筛下累计质量M1与碎屑总重量M之间满足以下关系：

(4)

两边取对数可得：

(5)

根据式(5),在对数坐标系内,混凝土碎屑的筛下累计重量与筛孔直径间满足线性函数关系,并且函数的斜率为(3-D)。

2.2 滚刀破碎能耗与分形维数的关系

盾构滚刀在破除混凝土时,刀盘的转动功率可通过盾构机数据采集系统实时获得,然而,对于单把滚刀破除单位体积混凝土所需的能耗的大小却难以确定。混凝土破碎过程滚刀所做的功W可表示为：

(6)

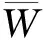
(7)

根据式(7),混凝土破碎能耗密度的大小与混凝土在不同工况下与滚刀相互作用时的应力～变形规律有关,根据相关研究[22-23],可认为混凝土等脆性材料在滚刀作用下发生破碎前始终处于弹性变形阶段,此时混凝土中应力与位移之间的关系可近似表示为：

(8)

将式(8)代入式(7),可得：

(9)

式中：σf为混凝土在滚刀作用下的表观破碎强度,该强度不仅与材料的无侧限抗压强度有关,还受到滚刀切削深度、刀间距以及切削速度的影响,因此难以确定。而根据文献[23],混凝土的表观破碎强度与其破碎分形维数有如下关系：

σf∝dD-3

(10)

式中：d为材料破碎前的特征直径,由于被滚刀破碎前的混凝土是整体块状而非颗粒状,此时可认为d为常数。因此,定义滚刀作用下混凝土破碎能耗密度(滚刀破除单位体积混凝土所做的功)与分形维数之间的关系为：

(11)

式中：α为混凝土破碎能耗系数;σc为被研究混凝土的单轴抗压强度。根据式(11),当得到混凝土在滚刀作用下的破碎分形维数后,可依据滚刀破碎不同强度等级混凝土时的做功数据拟合求得破碎能耗系数α。

3 盾构滚刀破碎混凝土试验

3.1 试验设备

滚刀破碎混凝土试验在盾构及掘进技术国家重点实验室的滚刀岩机作用综合试验平台上进行,该平台是用于评估和研究各型滚刀的破岩载荷、破岩效率及掘进控制的专用设备,如图1所示。

图1 滚刀破碎混凝土试验平台

该平台的主要测量系统包括载荷测量系统、位移测量系统、扭矩与转速测量系统以及功率测量系统;控制系统主要包括刀盘推进控制系统和刀间距控制系统,主要采用位移控制方式。平台的主要性能见表1。

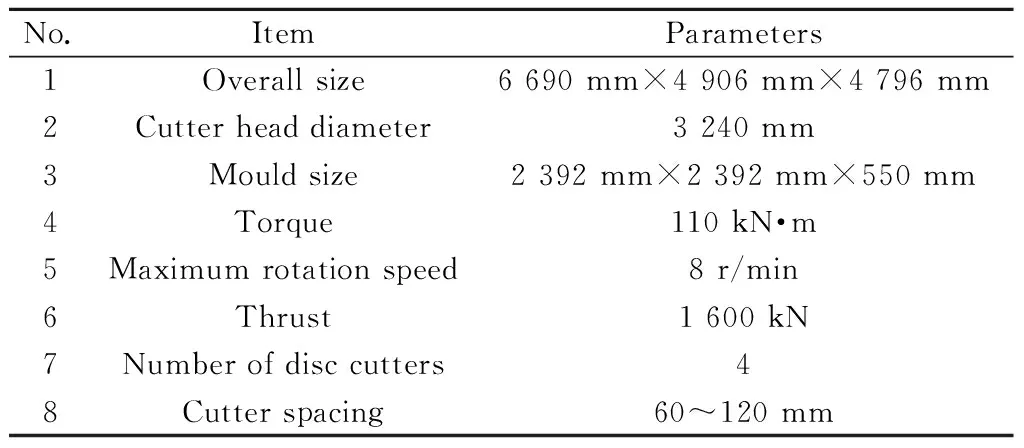
表1 试验平台性能参数

3.2 试样制备

试验中所用各强度等级混凝土均依据《普通混凝土配合比设计规程》(JGJ 55-2011)[24]与《砌筑砂浆配合比设计规程》(JGJT 98-2011)[25]配制,配制过程中所用砂为Ⅱ类天然砂,所用碎石为Ⅱ类碎石,经过筛分测试,其级配均符合相应的规范要求。材料配比及用量见表2。

表2 材料配比及用量

在浇筑上述两组材料箱中试样的同时,取部分相应材料制作边长为100 mm的立方体试块,每种材料制作3块(图2)。

图2 材料单轴抗压强度试块(左)及抗压试验(右)

在相同的室温条件下,经过28 d的洒水养护后,采用WAW-1000型万能试验机,按照普通混凝土力学性能试验方法标准(GB/T 50081-2019)[26]测试各种材料试块的单轴抗压强度,并取平均值作为相应材料的试验强度。最终确定的各材料的单轴抗压强度值见表3。

表3 材料单轴抗压强度

3.3 滚刀破碎混凝土工况设计

根据实际盾构掘进工程中掘进参数的控制范围,试验中推进速度取值为0.5～21.0 mm/min,刀盘转速取值为0.5～4.0 r/min,相应的滚刀贯入度取值为1.0～6.0 mm。同时,根据试验平台上滚刀的刀间距调节范围(60～120 mm),设计滚刀破碎混凝土试验的工况见表4。

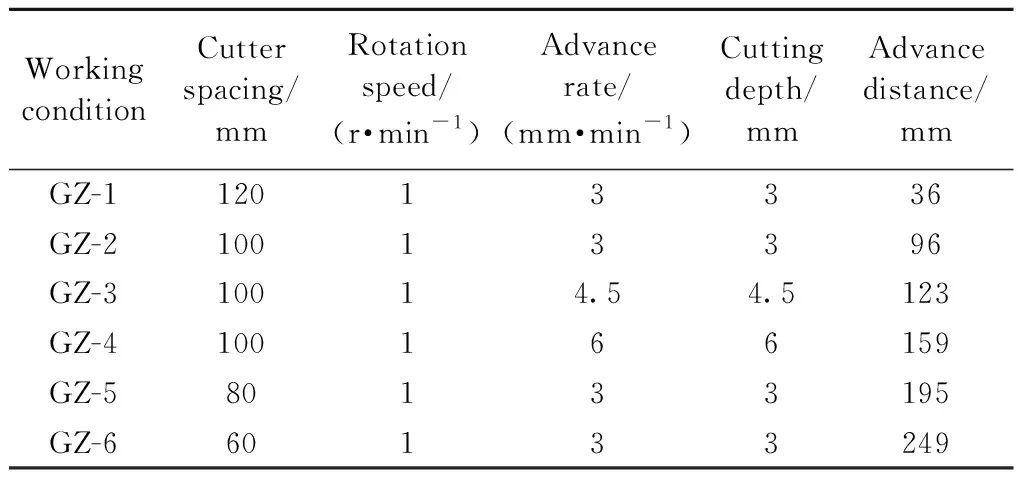
表4 滚刀破碎混凝土试验工况设计

试件养护完成后,按照表4中的工况设计采用滚刀岩机作用综合试验平台进行滚刀破碎混凝土试验,同步采集刀盘的的实时功率,并据此计算各滚刀在破碎混凝土过程中所做的总功。同时,为了防止混凝土切屑在试件上累积对试验数据产生干扰,在破碎间隙须及时清理混凝土碎屑(图3)。

图3 原型滚刀破碎混凝土试验 (a)滚刀破碎混凝土;(b)清理并收集切屑

4 混凝土破碎分形维数影响因素

采用组合振动筛将将滚刀掘进所得混凝土碎屑进行筛分,将筛分后的碎屑称重得到不同掘进工况下不同强度等级混凝土破碎之后的碎屑级配情况,筛分后的混凝土碎屑如图4所示。

图4 筛分后的混凝土碎屑

如图4所示,不同强度等级混凝土在采用不同滚刀贯入度工况进行掘进后,得到的混凝土碎屑在粒径分布上呈现较为明显的区别,例如,当滚刀贯入度h=3.0 mm时,M2.5混凝土碎屑最大粒径为312 mm,级配较为分散,而C30混凝土碎屑最大粒径为104 mm,且级配较为集中;对于滚刀掘进C15混凝土的情况,当贯入度h=1.0 mm时,混凝土碎屑最大粒径为113 mm,级配较为集中,而当贯入度h=6.0 mm时,混凝土碎屑最大粒径为266 mm,且级配较为分散。本研究根据碎屑级配信息,分析各因素对混凝土破碎分形维数的影响以及滚刀在掘进过程中的作功耗能情况。

4.1 混凝土强度对碎屑分形维数的影响

根据工况GZ-5中滚刀依次切削M2.5、M7.5、C15与C30四种不同强度等级混凝土所得的碎屑级配信息,得到ln[M(di)/MT]-ln(di/dmax)关系,如图5所示。

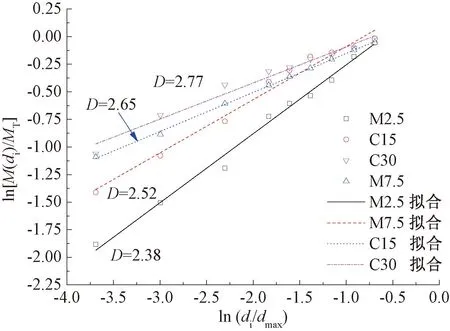
图5 不同强度混凝土碎屑级配信息

根据图5,对数坐标系内,混凝土碎屑的筛下累计重量与筛孔直径之间表现出良好的线性相关性,表明混凝土经滚刀破碎之后的碎屑颗粒形状满足统计意义上的自相似性,具有较好的分形特征。同时,碎屑的分形维数随混凝土单轴抗压强度的增大而减小。采用最小二乘法对级配数据点进行拟合,即可得到不同强度混凝土破碎后碎屑颗粒的分形维数D,拟合结果表明,随着混凝土单轴抗压强度的增大,滚刀破碎后碎屑的分形维数逐渐增大。

4.2 盾构滚刀贯入度对碎屑分形维数的影响

根据工况GZ-2、GZ-3、GZ-4中滚刀依次切削C15混凝土所得的碎屑级配信息,得到ln[M(di)/MT]-ln(di/dmax)关系,如图6所示。

图6 不同滚刀贯入度下混凝土碎屑级配信息

根据图6,碎屑的分形维数随滚刀贯入度H的增大而增大,说明当贯入度较大时,滚刀对混凝土的破碎较为充分,形成的碎屑颗粒尺寸更小,细颗粒含量更大。采用最小二乘法对级配数据点进行拟合,得到不同滚刀贯入度下混凝土破碎后碎屑颗粒的分形维数D,拟合结果表明,随着滚刀贯入度的增大,滚刀破碎后碎屑的分形维数也逐渐增大。

4.3 滚刀间距对碎屑分形维数的影响

根据工况GZ-1、GZ-2、GZ-5、GZ-6中滚刀依次切削C30混凝土所得的碎屑级配信息,得到ln[M(di)/MT]-ln(di/dmax)关系,如图7所示。

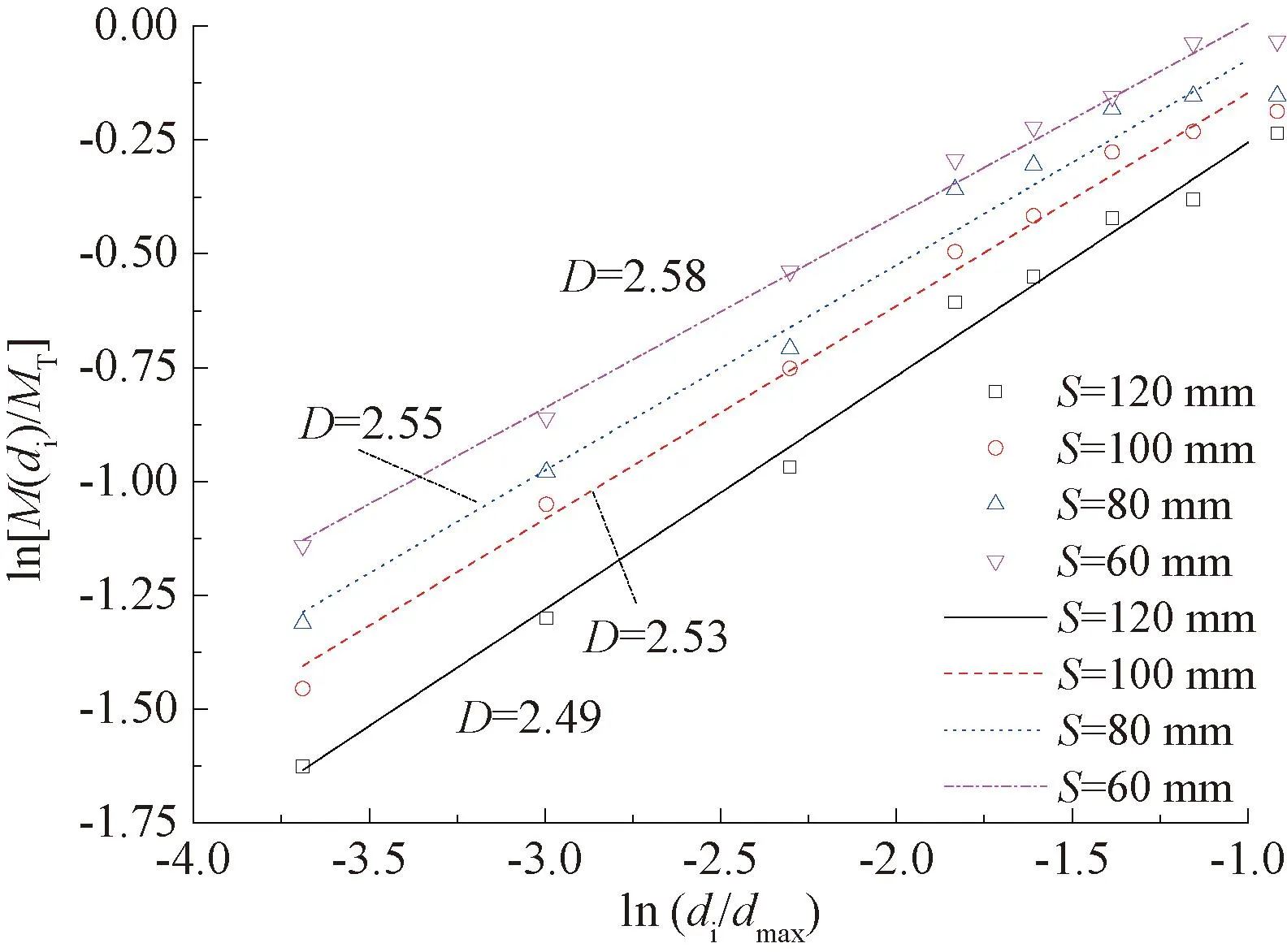
图7 不同滚刀间距下混凝土碎屑级配信息

根据图7,碎屑的分形维数随滚刀贯入度的增大而增大,说明当刀间距S较小时,4把滚刀共同作用下混凝土的破碎较为充分,形成的碎屑颗粒尺寸更小,细颗粒含量更大。采用最小二乘法对级配数据点进行拟合,即可得到不同滚刀间距下混凝土破碎后碎屑颗粒的分形维数D,拟合结果表明,随着滚刀间距的减小,滚刀破碎后碎屑的分形维数逐渐增大。

4.4 盾构滚刀作用下混凝土破碎能耗

相同体积的混凝土在滚刀作用下破碎时,由于破碎程度的不同,滚刀的破碎能耗也不同。为了得到滚刀在破碎不同强度等级混凝土过程中的能耗值,本研究对各安装在刀盘不同位置的滚刀荷载进行监测,监测所得数据如图8所示。

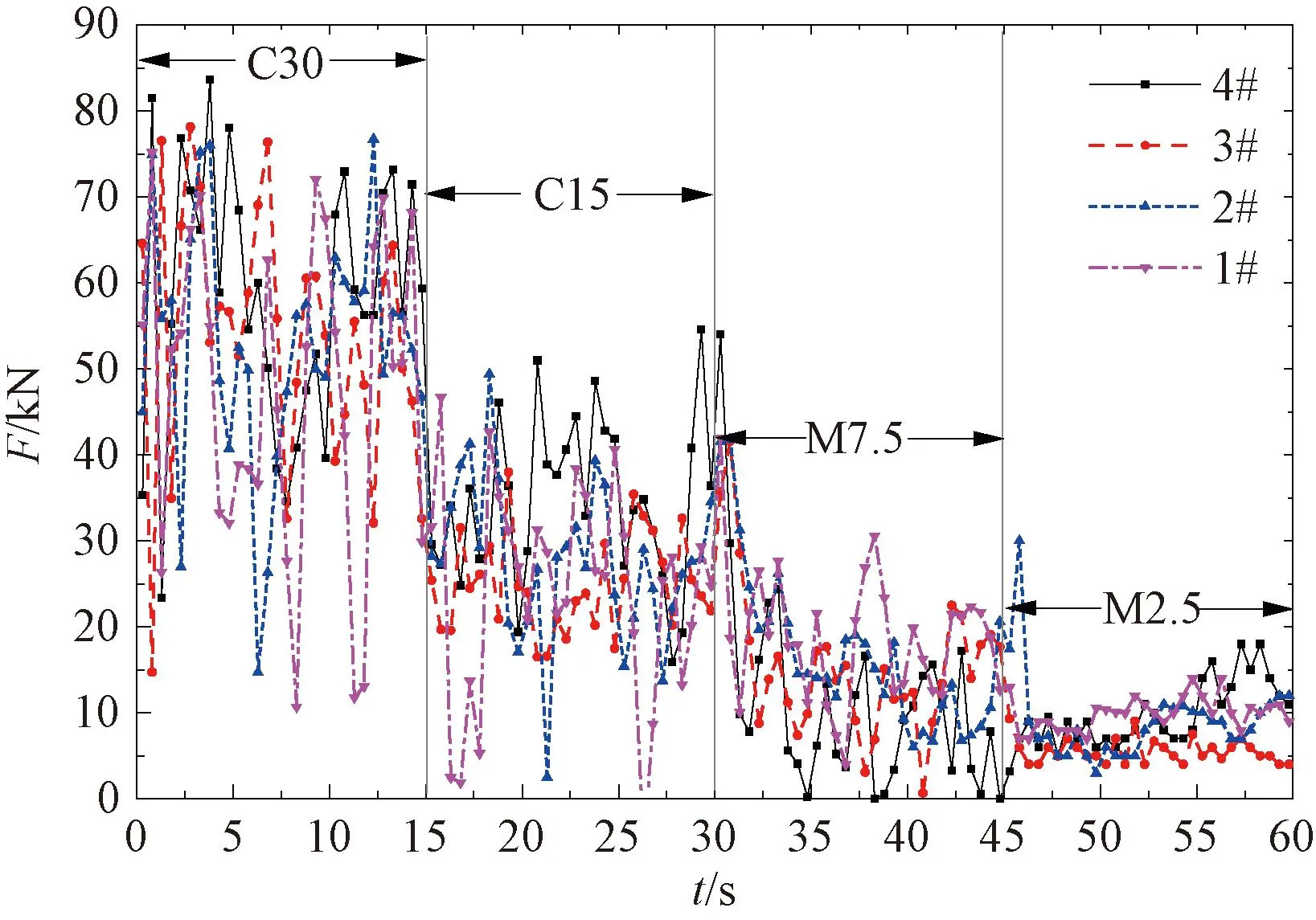
图8 滚刀荷载数据(滚刀安装位置分布从刀盘中心向边缘依次编号为1#～4#)

据监测数据计算得到4把滚刀在破碎各强度等级混凝土过程中所做的功,计算表达式为：

(12)

式中：Δt为滚刀荷载数据采集点的间隔时间;ω为刀盘转速;rj为j#滚刀在刀盘上的安装半径;Fij为j#滚刀第i个数据采集点的荷载值(采集点总数为n)。

(13)

式中：R1、R2分别为扇形混凝土破碎区域的外、内半径。将本研究滚刀掘进试验数据代入式(13)得到不同掘进工况下不同强度等级混凝土的破碎能耗密度,采用该结果对式(11)中α、d值进行拟合,结果如图9所示。拟合方法为：先取极限情况D=3,采用最小二乘法对能耗系数α进行拟合,然后将试验数据和α拟合值代入式(11)得到参数d的取值。

图9 混凝土的破碎能耗系数拟合

根据图9,滚刀破除混凝土时的能耗密度随混凝土强度增大而增大,并且通过拟合得到的能耗系数α取值为11.28,d的取值为0.928～0.947,可认为参数d为常数,反映了混凝土破碎能耗密度与碎屑分形维数之间的固定量值关系。然而,通过连接坐标原点与各能耗密度点的直线斜率可以发现,随着混凝土强度的增大,破碎能耗密度的增长率逐渐增大,即破碎能耗密度不仅与混凝土单轴抗压强度成正比,还受到材料碎屑分形维数的影响,并且随着混凝土强度的持续增大(如盾构刀具可能直接切削强度高达50～60 MPa的地下构筑物),分形维数对破碎能耗密度的影响越来越大。

因此,只需要通过筛分法测得任意工况下碎屑的分形维数,就可以根据式(11)计算得到该工况下滚刀破除不同强度混凝土的能耗密度,可为盾构隧道工程中临时支护结构混凝土强度的选择、盾构破除时掘进参数的设定以及所需匹配的刀盘功率与能耗评估提供理论参考依据。