新能源微电网多层级车网协同优化策略
2023-03-16朱永胜苗阳谢晓峰王东旭杨俊林王昊洋
朱永胜,苗阳,谢晓峰,王东旭,杨俊林,王昊洋
(1.中原工学院电子信息学院,河南郑州 450007;2.上海大学上海市电站自动化技术重点实验室,上海 200072)
0 引言
电动汽车(Electrical Vehicle,EV)作为低碳出行的首选近年来发展迅速[1],然而由我国一次能源利用现状可知,EV 直接入网不仅不易达到低碳的预期,而且会增大负荷峰谷差进而影响系统运行的安全稳定性[2]。对EV 接入新能源微网(New Energy Micro Grid,NEMG)进行统一调配管理可有效减缓规模化EV 入网所带来的消极影响,此策略不仅可实时消纳清洁能源达成真正的绿色低碳理念[3-4],还可利用车网互动(Vehicle-to-Grid,V2G)技术完成削峰填谷、提供辅助服务等目标,从而实现车网协同优化的多重效益[5-6]。
EV 作为一种交通工具,其使用主体是具有社会属性的群体,因此用户参与调控的积极性应放在考虑因素的首位。文献[7]提出车网互动激励价格机制,提升用户参与度系数后使EV 参与V2G 的激励价格与当前系统的削峰需求呈正相关增长趋势。文献[8]指出用户的积极性对EV 的参与度起决定作用,当参与度小于最低临界值时会使得网内负荷曲线偏离正常趋势。文献[9]计及用户满意度与配网安全性建立“配网—充电站”双侧架构,但模型中EV 的频繁充放电会对电池产生较大负面影响。目前较多研究将EV 并入NEMG,以达到加强NEMG 经济性和安全性、改善资源配置、调节系统综合性能的目的[10-14]。文献[15-18]对于EV 接入NEMG 的优化调度方式为集中式,随着参与电力系统调度的参与方类型日益丰富,各利益主体的设备隐私需求也随之增加,导致集中式调度难以获取参与方整体信息进而限制电力系统的优化,而多层级协同调度恰好可解决这一难题。
针对规模化EV 接入NEMG 的经济运行与负荷波动问题,本文提出考虑用户积极性的NEMG 多层级车网协同优化策略。根据各可调度单元属性的差异将EV、清洁能源等归纳至相应层级,每层充分考虑其运行特性设定相应调度指标,以达到多方互利共赢的目标,最后通过微网系统验证了所建架构的合理性与有效性。
1 多层级车网协同优化策略框架
本文所研究的多层级车网协同优化策略框架如图1 所示。其中,PL(t) 为经负荷层优化后的NEMG 功率,PNL(t)为经微网层优化后NEMG 功率。由图1 可知,所研究多层级车网互动系统包含风电机组(Wind Turbine,WT)、光伏机组(Photo Voltaic,PV)、燃气轮机(Micro Turbine,MT)、热电联产机组(Cogeneration Units,CU)、蓄电池(Storage Battery,SB)、智能充电桩等设备。本文调度的EV 根据用户上报给微网调控中心的数据分为EV 集群A 和EV集群B。当EV 集群A 用户第2 天有出行计划时,则需考虑用户出行需求;当EV 集群B 用户第2 天无出行计划时,则此集群中EV 为实时可控EV。负荷层对NEMG 原始负荷“削峰填谷”的同时优化EV用户积极性;微网层利用EV 与SB 的储能特性最大化消纳清洁能源以减小净负荷均值并缩减运行成本;配网层优化MT 与主网联络线出力来削减综合运行成本并减弱交互功率波动。
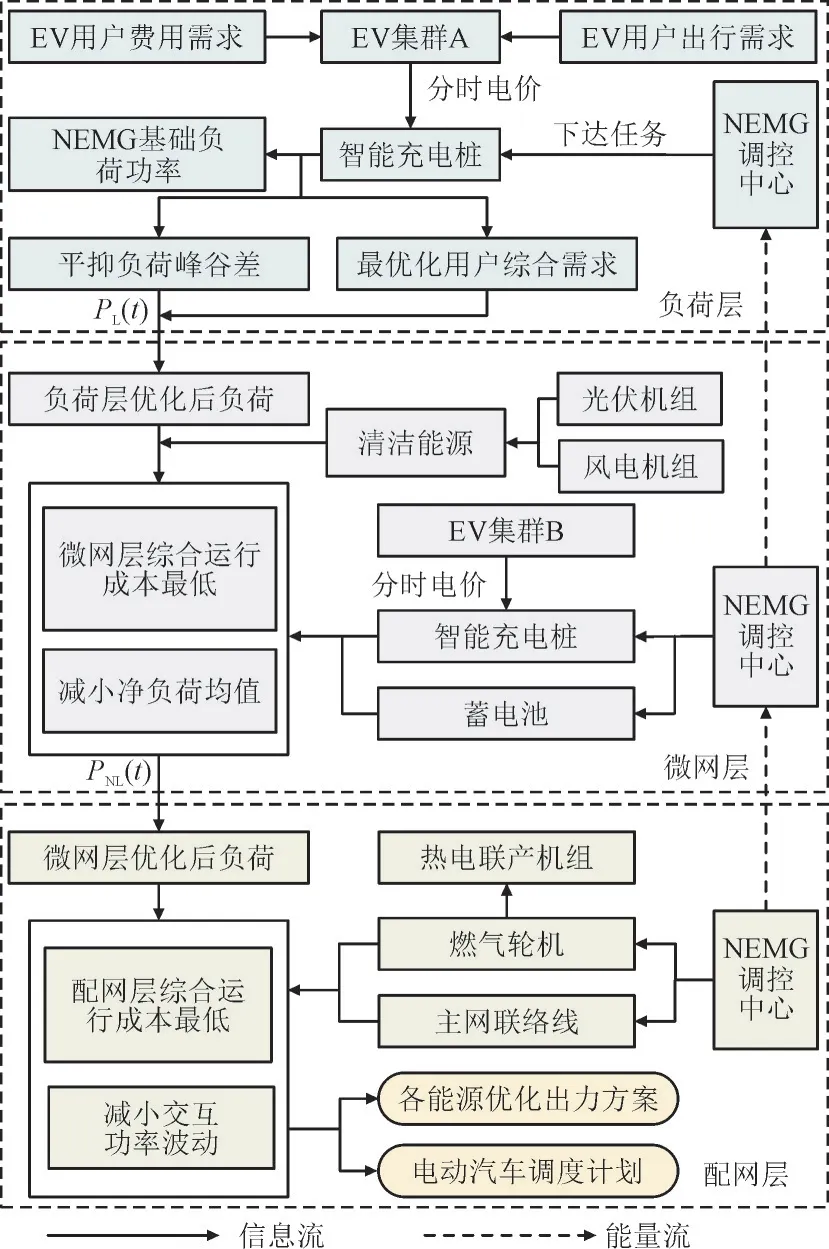
图1 多层级车网协同优化策略框架Fig.1 Framework of multi-level vehicle-grid collaborative optimization strategy
2 多层级优化调度策略
2.1 负荷层
2.1.1 EV用户积极性模型
负荷层将EV 作为调控负荷的手段。在负荷高峰时,制定较高交互电价促使EV 放电和减少充电行为;在负荷低谷时,制定较低交互电价促使EV 充电和减少放电行为,以达到通过分时电价引导EV 有序充放电来优化负荷曲线的目的。此策略需要EV 用户积极参与接受调度,便利性与经济性是影响用户参与积极性的2 个重要因素,因此EV 用户积极性模型由便利性与经济性构成,对应指标分别为EV 用户出行充电需求指标与EV 用户费用支出指标。
1)EV 用户出行充电需求指标为:
式中:Sout,i为第i辆EV 离网时荷电状态(State of Charging,SOC);Qm,i为日常行驶容量;Qs,i为电池容量;δ为不同SOC 的EV 离网时出行充电需求指数;Sb,i为用户预期SOC;Qr,i为备用行驶容量。
2)EV 用户费用支出指标为:
式中:Z为EV 数量;∂1和∂2分别为EV 用户出行充电需求指标系数和EV 用户费用支出指标系数。
2.1.2 EV荷电状态模型
EV 在行驶中,其行驶路程与车辆的SOC 呈现出线性关系[19],且EV 充电功率恒定。单辆EV 的SOC 模型为:
式中:Ech,i为第i辆EV 充电电量;Sin,i为第i辆EV入网时SOC;Si(t+1)为第i辆EV的t+1时段SOC;Si(t)为第i辆EV的t时段SOC;Δt为单位时段;η为EV 充放电效率;Pmax为EV 最大充放电功率;Tin,i与Tout,i分别为EV 入网、离网时刻。
2.1.3 EV出行行为时空随机性模型
EV 用户每天的离网时刻与入网时刻分别服从均值6.92、方差1.24 和均值17.47、方差1.80 的正态分布[15],则EV 出行行为时空随机性模型为:
2.2 微网层
2.2.1 优化目标
为保证系统经济性及充分消纳清洁能源,微网层以NEMG 运行成本最少和净负荷均值最低作为优化目标,其表达式为:
2.2.2 约束条件
1)SB 荷电状态约束为:
2)SB 出力上下限约束为:
3)EV 荷电状态约束为:
2.3 配网层
2.3.1 优化目标
为降低对主网的影响以及保证自身的经济性,配网层以MT 与主网联络线的综合运行成本最少和主网交互功率波动最小为优化指标,其表达式为:
式中:F3为MT 与主网联络线综合运行成本的目标函数;F4为主网交互功率波动的目标函数;CCO,CEN,CRMT分别为配网层发电费用、环境治理总费用、供热的额外收益;PGRI(t)为t时段微网与主网间传输功率。
配网层发电费用CCO的表达式为:
式中:CMT为MT 发电费用;CGC为联络线交互费用;ψG和WLHV分别为天然气价格与低热值;ηMT,,PMT分别为MT 的效率、在t时段功率、装机费用、额定功率;fMT为容量因子;h为折旧率;u为有效使用期限;KMT为单位运维费用系数;分别为向主网购、售电价格;分别为购、售电状态。
传统能源发电会带来COx,SO2,NOx等一系列污染物,为实现绿色低碳理念,扩大清洁能源入网规模,引入环境治理费用CEN为:
式中:j为污染物种类;J为污染物种类总数;Cj为处理第j类污染物单位费用;λMT,j和λgri,j分别为MT和主网联络线污染物的单位排放量。
燃气轮机提供电能的同时还可进行热电联产,以实现能量梯级利用,计算供热额外收益CRMT为:
式中:ψR为供热售卖价格;KR为供热系数;ηre为余热回收效率;Klos为热量散失系数。
2.3.2 约束条件
1)传输功率约束为:
2)MT 出力约束为:
3)MT 爬坡约束为:
式中:PMT(t-1)为MT在t-1 时刻的功率;为MT 最大爬坡功率。
4)NEMG 购、售电状态变量约束为:
5)功率平衡约束为:
3 求解方法
采用蒙特卡洛模拟算法和多目标粒子群优化(Multiobjective Particle Swarm Optimization,MPSO)算法联合求解本文所建模型。使用前者求解负荷层模型;后者求解微网层和配网层多目标、高维、非线性、多约束的优化模型,并在求解同时对算法进行改进。
3.1 改进粒子更新策略
为使标准MPSO 算法在全局与局部都拥有较均衡的搜索能力,本文根据迭代次数y的不同来实时动态调节惯性权重,此方案可在算法前期保持多样性、后期保持较好收敛性和搜索准确,惯性权重ω的调节表达式为:
式中:ωmin与ωmax分别为惯性权重最小值与最大值;y为迭代次数;ymax为最大迭代次数。
3.2 时变变异
考虑到MPSO 算法易在运算初期陷入局部最优,优选1 种时变变异算子ξ。将粒子变异通过调节算子来实现,其步骤如下:
1)选取位于[0,1]区间随机数赋值给r1,r2。
2)当ξ>r1,则在1 和决策变量维数n间取整数k;若ξ<r1,则继续变异循环。
3)对第a个粒子的第k维位置Xa,k利用Xa,k=Xmin+(Xmax-Xmin)r2进行变异。Xmin,Xmax分别为粒子a位置的最小值和最大值。
多层级车网协同优化策略仿真计算流程如图2所示。
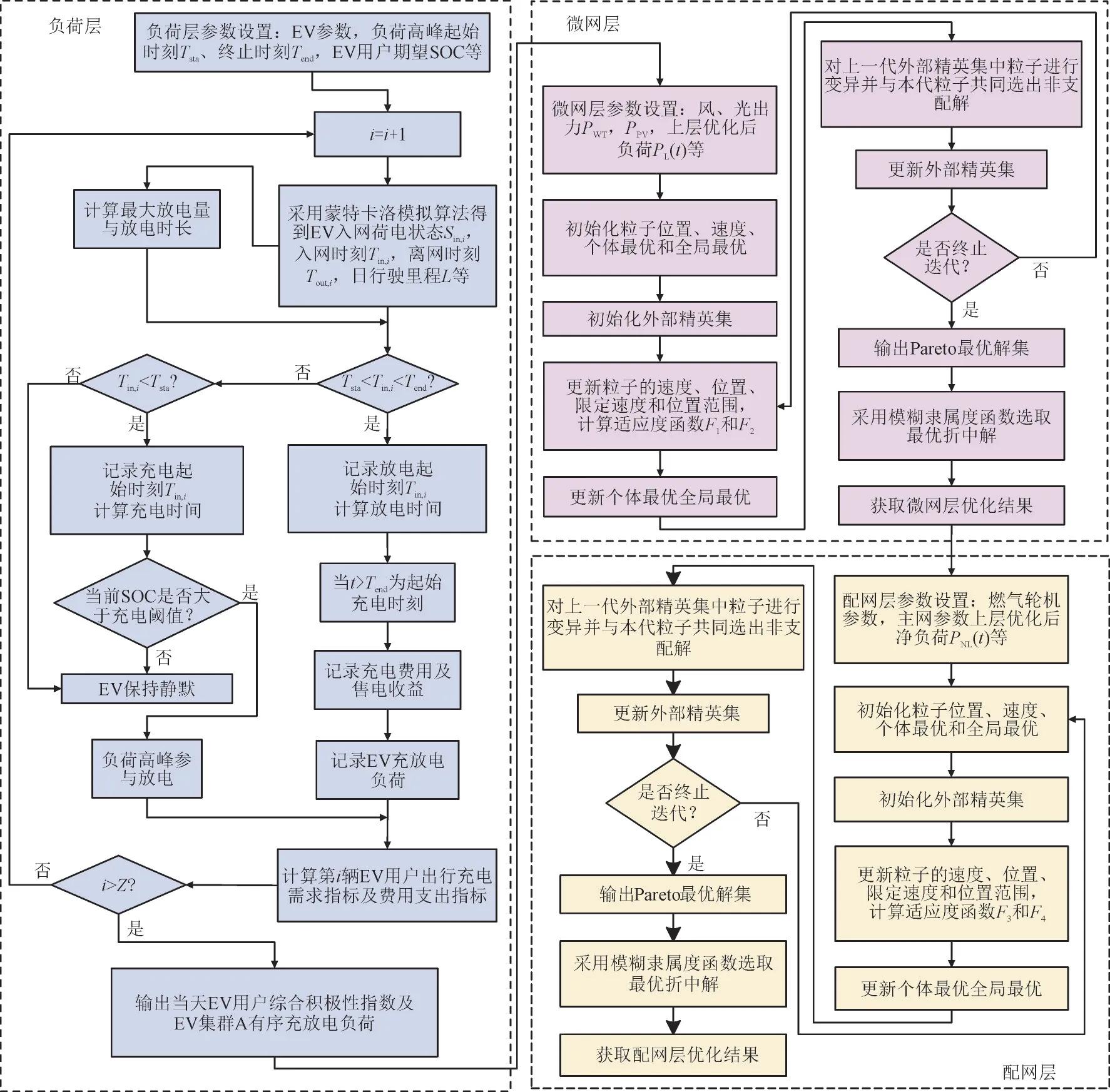
图2 多层级车网协同优化策略仿真计算流程Fig.2 Simulation calculation process of multi-level vehicle-grid collaborative optimization strategy
4 算例分析
4.1 参数设定
本文以某并网型NEMG 为例,得到EV 相关参数、NEMG 系统各单元相关参数、污染物排放及处理参数[20-25]分别如表1—3 所示。

表1 EV相关参数Table 1 Related parameters of EV
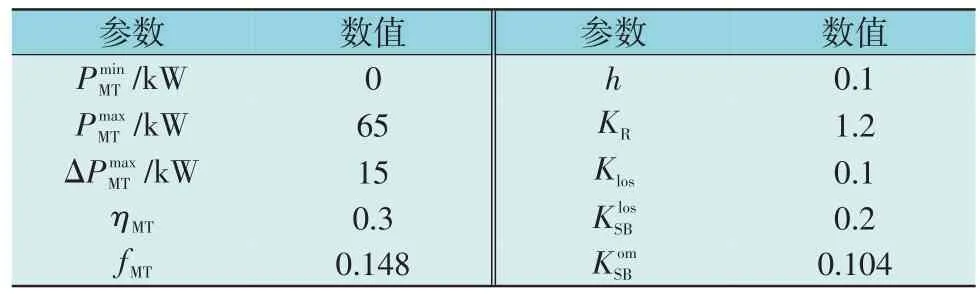
表2 NEMG系统各单元相关参数Table 2 Parameters related to each unit in NEMG system

表3 污染物排放及处理参数Table 3 Parameters of pollutant discharge and treatment
4.2 实验结果分析
4.2.1 负荷层优化结果
在负荷层对EV 集群A 进行3 方面比较,分别为综合指标最优的EV 有序充放电调度、用户便利性最优的EV 无序充电调度和用户经济性最优的EV 有序充放电调度。以原始负荷为参照,3 种调度方案的负荷曲线如图3 所示。

图3 3种调度方案的负荷曲线Fig.3 Load curves of three dispatching schemes
由图3 可知,在用户便利性最优情况下,EV 的充电时间集中在8:00—12:00 与18:00—22:00,此充电时间与用户工作生活规律高度重合,该充电模式进一步加剧负荷“峰上加峰”,对NEMG 产生消极作用。在用户经济性最优情况下,EV 的充电时间集中在电价低谷的22:00—24:00 与1:00—6:00,为获取收益在电价高峰的17:00—21:00 时段内放电,因“同群效应”的影响此方案将会产生新的负荷峰谷。在综合指标最优情况下EV 负荷可进行转移,当负荷高峰时,符合条件的EV 可向NEMG 输送部分电能,以缓解高峰负荷带来的负面影响并可产生一定收益,度过负荷高峰时段后EV 可在电价较低时段充电,以满足出行需求并可减少用电费用支出。
3 种方案的指标对比如表4 所示。
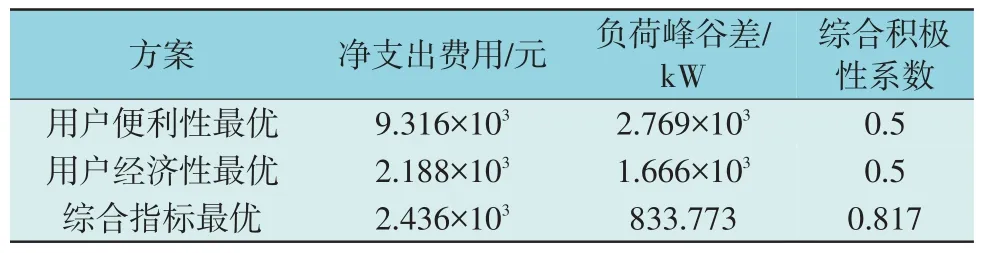
表4 3种方案的指标对比Table 4 Comparison of indicators among three schemes
由表4 可知,综合积极性系数越大代表用户参与调度的积极性越强烈。用户便利性最优方案的净支出费用与负荷峰谷差均为最大值。用户经济性最优方案与综合指标最优方案相比,虽然净支出费用略低但负荷峰谷差较大,因此对NEMG 产生的消极影响较大。由上述方案对比可知,本文所提方案不仅兼顾用户出行便利性与经济性,令用户积极性综合指标达到最大,更使EV 合理充放电达成“削峰填谷”的目标。
4.2.2 微网层优化结果
将负荷层优化得到的EV 充放电功率与基础负荷叠加传送至微网层,与该层的风光出力共同组成净负荷。微网层采用第3 节所述方法求解,通过调控SB 以及EV 集群B 的出力来进行净负荷的优化配置,取微网层运行成本为1.540×103元、净负荷均值为613.03 kW 为最优折中解。
微网层各单元出力曲线如图4 所示。
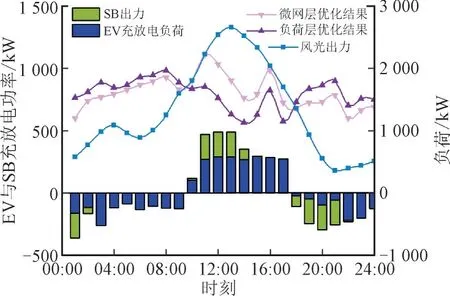
图4 微网层各单元出力曲线Fig.4 Output curves of each unit at microgrid layer
由图4 可知,EV 与SB 在风光出力较低的时段18:00—24:00 与1:00—9:00 放电,该时段内清洁能源供给量小于NEMG 负荷的需求量。EV 与SB 在清洁能源出力盈余的时间段10:00—18:00 充电,该时段内清洁能源供给量大于NEMG 负荷的需求量。优化后的NEMG 负荷曲线大体上已贴合清洁能源出力态势,可达到尽可能多消纳清洁能源以降低运行成本与碳排放的目的。
4.2.3 配网层优化结果
将微网层优化得到的NEMG 净负荷传送至配网层,该层调度单元为MT 与交互功率。配网层与微网层求解方法相同,取配网层运行成本为1.710×104元、交互功率波动为412.348 kW 为最优折中解。
配网层各单元出力曲线如图5 所示。

图5 配网层各单元出力曲线Fig.5 Output curves of each unit at distribution network layer
由图5 可知,相对于主网发电的大量污染物排放,MT 发电不论污染物排放量还是运行成本都相对较低,其在每个净负荷为正的时段均有出力,当不足以支撑需求量时才从主网购买。在10:00—17:00这个时间段内,清洁能源出力充沛而微网层不足以完全消纳,此时将电能出售给主网,不仅可以获取收益提升经济性还可完全消纳清洁能源,杜绝弃风、弃光现象的发生。在18:00—24:00 与1:00—9:00 这2 个时间段内MT 几乎一直处于全额出力状态,但由于机组数量限制与净负荷较大,主网出力还是占据主要部分。
4.2.4 对比分析
将NEMG 不分层级调度策略与本文所提的NEMG 多层级调度策略的结果进行对比,2 种策略下NEMG 运行结果对比如表5 所示。
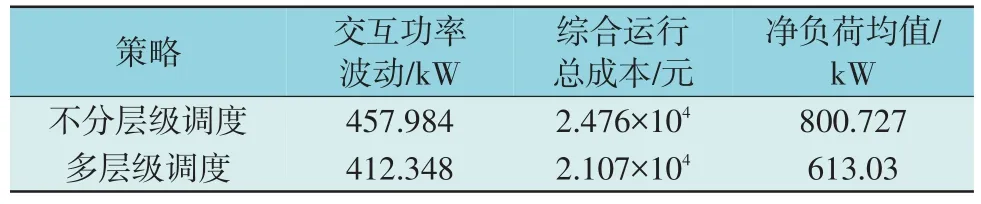
表5 2种策略下NEMG运行结果对比Table 5 Comparison of NEMG operating results under two strategies
由表5 可知,与本文所提策略运行结果相对比,采用不分层级调度策略时其交互功率波动扩大11.1%、系统综合运行成本增加17.5%、净负荷均值扩大30.5%。通过数据对比说明不分层级调度策略各项指标均远不及本文所提多层级调度策略。
5 结论
本文针对规模化EV 接入NEMG 的经济运行与负荷波动问题,提出一种考虑用户积极性的NEMG 多层级车网协同优化策略。负荷层虑EV 用户积极性前提下,改善了EV 充放电计划;微网层调动储能与EV 最大化消纳清洁能源以实现低碳理念并节约成本;配网层调度分布式电源出力以减少运行成本、稳定交互波动。通过算例分析所得结论如下:
1)所提考虑EV 用户积极性模型令用户积极性大幅提升,不仅在实现“削峰填谷”目标中发挥良好作用,还使EV 充放电调度更加贴合实际。
2)通过与不分层级调度策略对照,本文所提多层级调度策略调节了系统的综合性能,可实现系统经济性、稳定性、环境效益等方面的互利共赢。
