基于改进麻雀搜索算法优化RBF神经网络的光伏阵列故障诊断
2023-03-16武文栋施保华郑传良郭茜婷陈峥
武文栋,施保华,郑传良,郭茜婷,陈峥
(1.三峡大学电气与新能源学院,湖北宜昌 443002;2.福州大学电气工程与自动化学院,福建福州 350108;3.国网宁德供电公司,福建宁德 352100;4.湖北省微电网工程技术研究中心,湖北宜昌 443002)
0 引言
在“双碳战略”目标下,寻找和利用新型清洁的可再生能源已成为当今世界的主要研究热点[1-3]。近年来,我国光伏发电技术的进步和光伏并网发电规模的不断扩大,使得在恶劣的自然环境下工作的光伏阵列面积大、分布广,容易出现组件短路、开路、老化和局部遮阴等故障[4-5]。这些问题对光伏电站整体的运行和发电效率产生了较大影响,因此高效准确地对光伏阵列故障进行诊断具有重要的意义。
文献[6]提出改进径向基函数(Radial Basis Function,RBF)神经网络的故障诊断方法,具有较小的诊断误差,但易陷入局部极小值,甚至在某些条件下劣化诊断结果。文献[7]提出改进BP 神经网络的光伏阵列多传感器故障检测方法,优化了诊断精度,但对于大型光伏电站的检测成本较高,难以规模化应用。文献[8]引入高斯核函数提高了支持向量机对故障分类和识别的效果,但高维映射导致寻优速度变慢。文献[9]考虑了改进遗传算法优化BP神经网络的故障诊断方法,将交叉和变异概率进行了自适应调整以有效诊断故障,但不同光伏电站因配置和结构不同而导致阵列输出特性不同,因此该方法在不同光伏发电站应用时需要进一步优化。
BP 神经网络在计算训练时可能会有收敛到局部最优解、迭代速度慢和诊断精度较低等问题[10],而RBF 神经网络具有学习的收敛速度快、泛化能力强、几乎可以逼近任意非线性函数等优点,因而被广泛地应用于预测控制、系统建模和故障诊断等领域。文中提出一种基于改进麻雀搜索算法优化RBF 神经网络(Improved Sparrow Search Algorithm Optimized Radial Basis Function Neural Network,ISSA-RBF)的方法,分析光伏阵列的输入和输出特性,构建故障诊断模型,并用ISSA-RBF 的径向基宽和权重向量,增强网络动态性能,提高光伏阵列故障诊断精度。
1 光伏阵列故障诊断模型的构建
1.1 仿真模型构建
本文通过Matlab/Simulink 搭建出6×4 的光伏阵列仿真模型,设置故障模拟时的光伏阵列光照强度在200W/m2~1 000 W/m2的区间内,各个阵列模块的环境温度在25 ℃~45 ℃的区间内。单个组件模块的参数设置为:最大功率点电压Umpp为32.8 V、最大功率点电流Impp为7.5 A、开路电压Uoc为41.5 V、短路电流Isc为7.9 A。光伏阵列故障仿真模型如图1 所示。
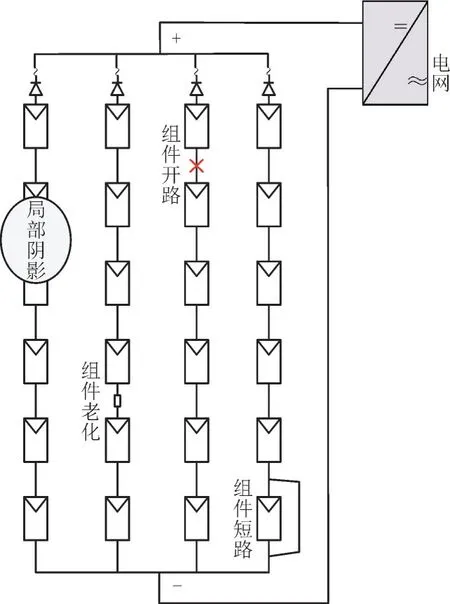
图1 6×4的光伏阵列仿真模型Fig.1 Photovoltaic array simulation model with 6 rows and 4 columns
作为数据驱动故障诊断方法,故障特征量的提取是确保模型有效的重要前提。本文主要通过对不同工作状态下的光伏阵列I-U曲线和P-U曲线的分析来提取故障诊断模型的特征参数[11-15]。拟设置4 种不同的光伏阵列常见故障类型,分别为阵列局部阴影、组件老化、组件开路、组件短路。局部阴影故障通过减小部分光伏阵列的光照强度来模拟;老化故障通过在某条支路上增加5 Ω电阻来模拟;开路故障通过断开故障光伏阵列与其相邻光伏阵列的导线来模拟;短路故障通过将故障光伏阵列的正负极短接来模拟。
通过仿真运行,获得正常和各个故障状态下光伏阵列的I-U曲线和P-U曲线,如图2 和图3 所示。
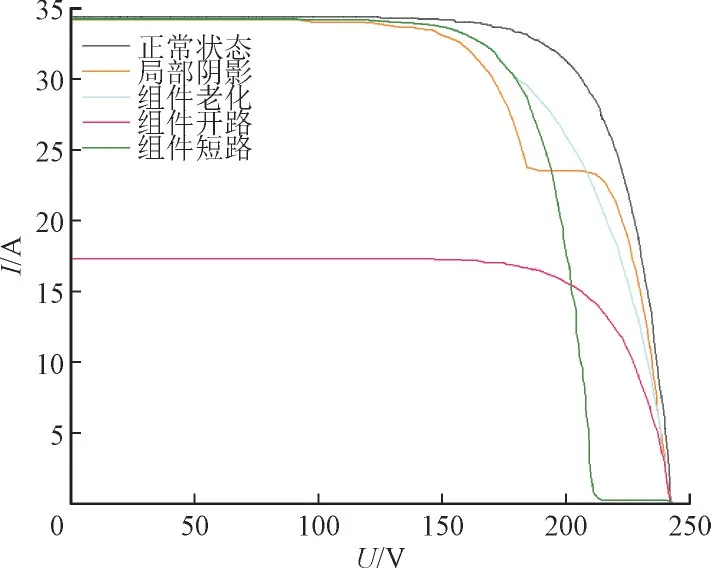
图2 正常与各故障状态下I-U曲线Fig.2 I-U curves under normal and different fault states
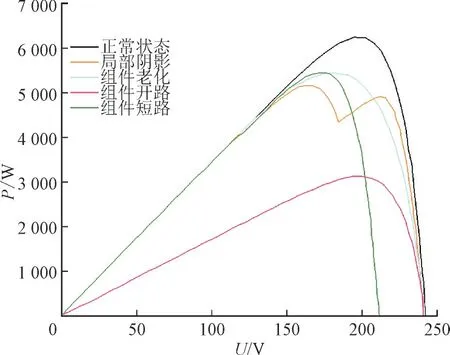
图3 正常与各个故障状态下P-U曲线Fig.3 P-U curves under normal and different fault states
由图2 和图3 可知,当光伏组件发生局部遮挡时,I-U曲线会出现“多膝”现象,光伏阵列的P-U曲线会出现“多峰”现象,并且光伏阵列的最大功率点电压和最大功率点电流显著减小。当光伏组件发生老化故障时,光伏阵列的最大功率点电压会显著降低。当光伏组件发生开路状况时,光伏阵列的最大功率点电压不变,但其短路电流会明显减小。当光伏阵列出现组件短路情况时,光伏阵列的短路电流基本不变,而开路电压和最大功率点电压会减小。
因此,不论发生哪类故障,均会导致光伏阵列的最大功率点电压值Umpp、最大功率点电流Impp、开路电压Uoc、短路电流Isc中的若干变量发生明显变化,故障模型的特征参数选择这4 个变量作为ISSA-RBF 故障诊断模型的输入层变量。同时根据光伏阵列的故障类型,相应定义了诊断模型的5 个输出层变量。该网络故障诊断模型的输出层变量如表1 所示。
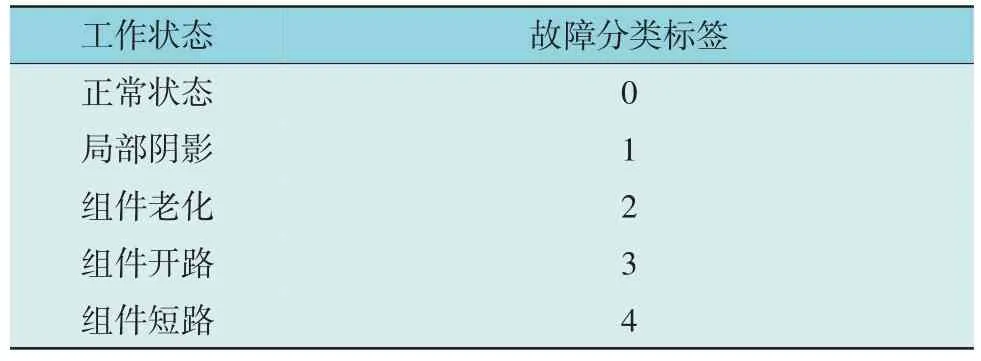
表1 模型的输出层变量选取Table 1 Variable selection of model output layer
1.2 RBF神经网络诊断模型结构设计
RBF 神经网络是一种前馈型神经网络,主要由输入层、隐含层和输出层构成,其中隐含层到输出层之间权重向量是线性的,可以加快网络的学习速度,避免网络的过拟合现象[16-17]。针对已经提取的光伏阵列故障特征参数,构建如图4 所示的RBF 神经网络故障诊断模型。
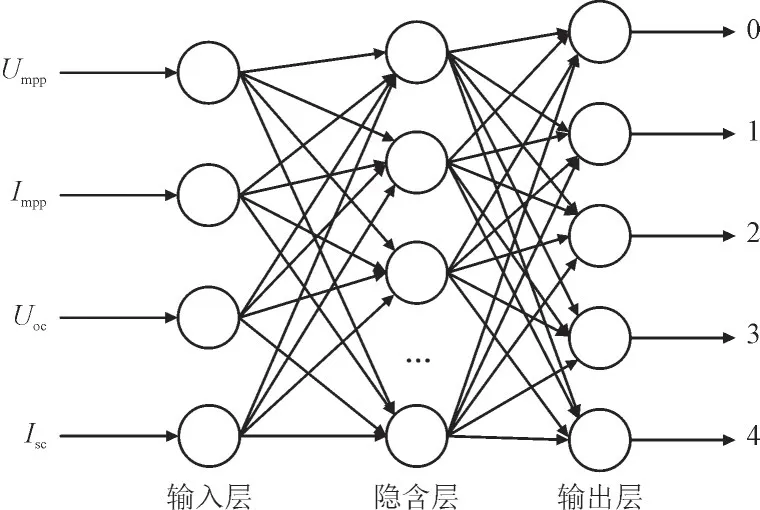
图4 RBF神经网络的结构Fig.4 RBF neural network structure
RBF 神经网络结构中的径向基函数一般选择采用高斯基函数:
式中:R(x-ai)为隐含层第i个节点的输出;ai为第i个径向基函数的中心矢量;bi为第i个径向基函数的参数宽度;‖x-ai‖为输入量x与基函数中心矢量ai间的欧氏距离。
RBF 神经网络的输出为:
式中:wi为权重的连接权重值;h为隐含层节点数;θj为输出层第j个节点的阈值;yj为实际输出值。
RBF 神经网络关键的是径向基函数的选取[15],一般将高斯函数作为RBF 的径向基函数,因此隐含层节点中高斯核函数的中心和宽度、以及隐含层到输出层的连接权重就直接决定了RBF 神经网络分类模型的动态性能。在多输入多输出的高维非线性工程中,高斯核函数参数的优化至关重要,本文提出一种基于ISSA-RBF 高斯核函数参数方法。
2 算法原理与改进
2.1 麻雀搜索算法基本原理
根据自然界中麻雀群体觅食和反捕行为,薛等人于2020 年提出了麻雀搜索算法[18-21](Sparrow Search Algorithm,SSA)。它是一种模拟麻雀群体行为的智能优化算法,具有良好的全局寻优能力、收敛过程迅速,稳定性好等优点,因此常被用于解决具有多峰的非线性优化问题,同时能有效优化RBF 神经网络径向基函数的参数选取。
麻雀群体觅食过程中有明确的劳动分工:发现者、追随者和预警者。由于发现者作为种群的觅食向导,为了更新觅食搜索范围,需要不断搜索广阔的区域并更新它们的位置。因此在麻雀种群迭代计算时,发现者的位置更新公式为:
式中:为麻雀种群中的第n个元素值;itermax为种群可迭代极值数;α1和α2为(0,1)间的均匀随机数;R2(R2∈[0,1],单只麻雀个体的随机值)和ST(ST∈[0.5,1])分别为危险性和安全性的范围值;c为服从正态分布的随机数
追随者的位置更新公式为:
预警者的位置更新公式为:
式中:β为符合正态分布性质的步长控制参数;K∈[-1,1]是一个随机数值;fi,fb,fw分为当前第i只麻雀的适应度值、当前全局最优适应度值和最劣适应度值;ε为无限接近但不等于0 的常数。
2.2 改进SSA
在采用SSA 解决工程实际问题中,麻雀个体收敛速度过快容易收敛到局部极值点使算法进入“早熟”,常出现收敛精度不高的问题。此外,在算法迭代末期由于麻雀个体仅在区域内的较小范围进行局部搜索,导致算法收敛速度降低,难以获取全局最优解。因此,本文对SSA 进行改进,采用以下2个策略提升SSA 的全局寻优能力。
1)在算法初期,通过融合Levy 飞行策略[22-23]对麻雀种群初始化,使得发现者位置更加随机多样,部分麻雀个体可在区域内较大范围进行全局搜索,扩大了发现者搜索区域,提高种群总体的寻优效率。更新后的发现者公式为:
式中:δ为一个步长参数;Levy(s)服从莱维分布。
飞行步长公式为:
式中:μ和v均为[0,1]间的标准正态分布随机数;常数τ=1.5;σ为一个关于Γ函数和τ的常函数。
2)针对算法末期可能出现停滞现象而易陷入局部最优,引入自适应权重φ,增强麻雀种群全局收敛能力,使得麻雀在当前最优位置附近范围进行随即搜索。控制惯性权重φ可调节麻雀搜索算法的全局与局部寻优能力,当φ值较小时,全局寻优能力增强而局部寻优能力减弱;当φ值较大时,结果相反。因此在麻雀发现更优位置时则更新当前位置,否则麻雀位置保持不变,从而提高种群跳出局部极值点束缚的概率。该设计使得算法在迭代后期能以较大概率在全局范围内避免因麻雀群体的聚集导致种群多样性缺失,增强了算法的全局搜索能力。其中自适应权重φ的调整公式为:
式中:φmin和φmax分别为自适应权重的最小值和最大值。
其中,若在当前位置麻雀追随者较少,则将自适应权重增大,更新其位置,增强全局寻优能力。
更新后的追随者公式为:
改进的SSA 流程如图5 所示。
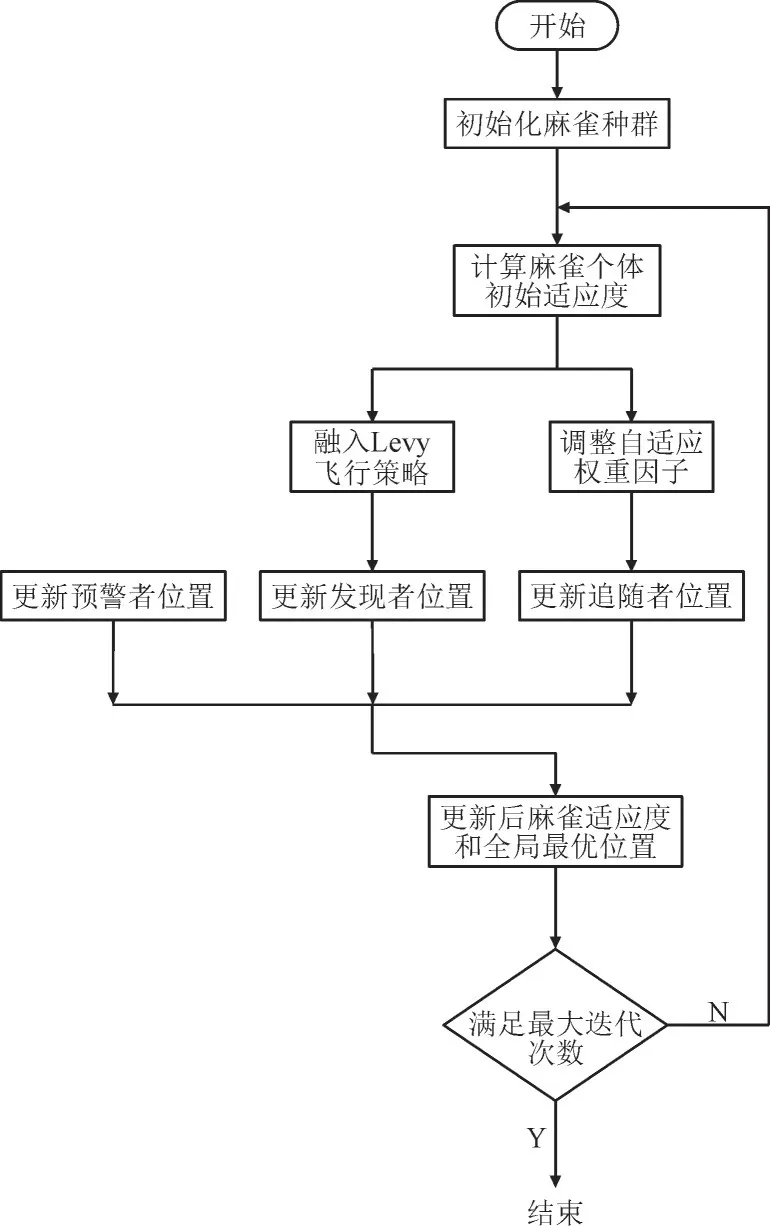
图5 改进麻雀搜索算法流程图Fig.5 Flow chart of improved sparrow search algorithm
2.3 ISSA-RBF神经网络
文中利用改进的SSA 对RBF 神经网络的径向基宽和连接权重进行优化求解,形成更加高效的组合训练模型。选取该模型的期望输出值和实际输出值的均方差为目标函数即适应度值,利用麻雀群体的聚集来确定径向基宽和连接权重,当均方差值最小时,就确定了RBF 神经网络的一组理论最优参数。
ISSA-RBF 神经网络模型的具体实现步骤如下:
1)数据预处理。对采集的原始特征参数进行数据预处理,加快网络模型的收敛速度。
2)算法初始化。初始化麻雀搜索算法参数和RBF 神经网络径向基函数参数。
3)更新麻雀位置。根据改进麻雀搜索算法的位置更新方法更新麻雀个体当前位置,并作为RBF神经网络的径向基宽来训练网络。
4)计算适应度值。将RBF 神经网络故障模型的输出结果计算个体适应度值。
5)更新麻雀最优位置与适应度值。在寻优迭代过程中,对麻雀的位置向量和适应度值进行更新。
6)确定RBF 神经网络最优参数。重复步骤2)—5),直到达到网络最大迭代次数或满足网络设定精度,停止迭代,输出理论最优参数。
3 仿真实验分析
3.1 数据样本选取
故障诊断仿真模型搭建完成后,从实际分布式光伏发电系统中收集到1 组典型样本数据,如表2所示。使用该组数据对各类故障状态分别进行模拟。在5 种工作状态下分别采集到120 组数据,共采集到600 组故障数据,取出每种不同故障状态下的75 组数据作为故障诊断的训练样本,其余45 组数据作为该模型的测试样本。
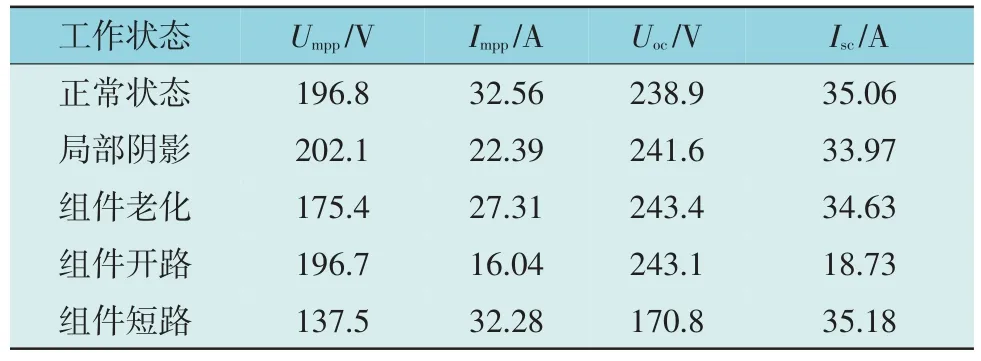
表2 光伏阵列仿真的典型样本数据Table 2 Typical sample data for photovoltaic array simulation
3.2 实验过程及诊断结果
将网络的最大迭代次数设为200,学习率设为0.1,麻雀种群规模设为40。利用3.1 节采集到的数据集,在RBF 神经网络结构中进行迭代训练,将训练结果与传统BP 和SSA-RBF 模型的训练结果进行对比。由于RBF 神经网络输入层特征参数的单位不统一,数量级差距过大,若直接用该组数据进行迭代训练会导致网络模型的收敛性变差,因此需要对该组数据进行去量纲处理,增强RBF 神经网络的泛化能力[24-27]。
经过仿真实验得到3 种模型的适应度曲线,如图6 所示。由图6 可以看出,ISSA-RBF 神经网络模型的曲线变化更为陡峭,在迭代35 次左右就趋于稳定,说明可以更好地跳出局部极值点,能够以更快的速度收敛到全局最优,同时适应度达到0.6左右,很好地满足了精度要求;而SSA-RBF 模型在迭代接近50 次才趋于稳定,且适应度约为0.62;传统BP 模型在迭代105 次左右才能趋于稳定,适应度仅为0.65,收敛精度较差。综上分析可知,ISSARBF 神经网络诊断模型收敛所需迭代次数较SSARBF 模型、BP 模型分别减少了15 次和70 次,因此该模型与其他模型相比,有更快的收敛性和更高的诊断精度。
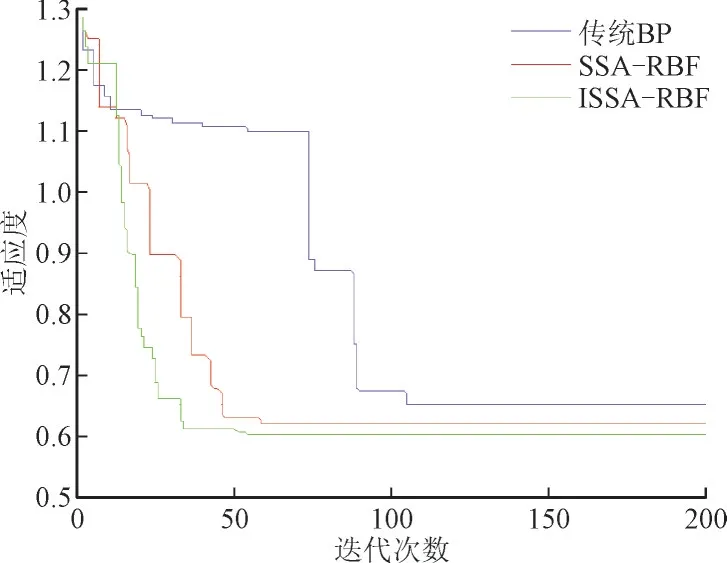
图6 3种模型的适应度曲线Fig.6 Fitness curves for three models
对故障特征参数的样本数据进行训练后,将其余225 组测试集数据输入到3 种模型,得到了测试集的故障诊断分类结果,如表3 所示,3 种模型的平均诊断精度分别为83.5%,90.6%和94.8%。
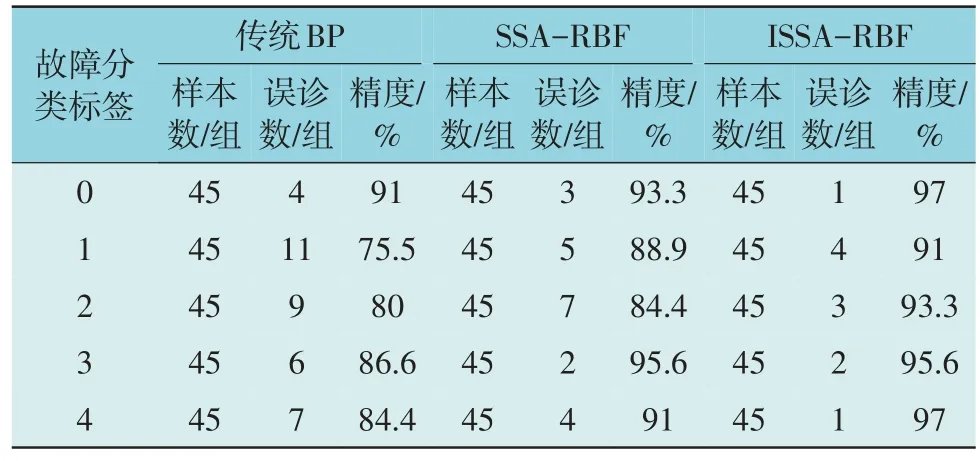
表3 3种模型的诊断精度Table 3 Diagnostic accuracy of three models
对表3 进行对比分析,可得到如下结果
1)在相同样本数据集下,ISSA-RBF 和SSARBF 模型的诊断精度都达到了90%以上,均高于传统BP 模型的83.5%。ISSA-RBF 和SSA-RBF 模型是由于SSA 优化了RBF 神经网络的径向基宽和连接权重,使得网络中的基函数可以更好地将光伏阵列的故障数据分解为不同维度上的细节信息,从而理论上可以不断逼近实际故障类型的输入输出非线性映射关系。
2)开路和短路2 种故障状态的诊断精度都明显高于局部阴影和组件老化2 种故障的诊断精度。这是因为:当出现开路故障时,Impp出现显著降低;当出现短路故障时,Umpp出现显著降低,即这2种故障类型均有明显特征,易于诊断。而局部阴影和老化故障由于受多种因素影响,在低温和弱光照条件下,使得RBF 神经网络无法较高精度地将其与正常状态区分出来,所以更易出现误诊断,诊断难度较大。
3 种模型的测试集输出结果预测如图7 所示。ISSA-RBF 模型在测试的225 组数据中仅11 组数据误诊断,SSA-RBF 模型出现21 组数据误诊断,而传统BP 模型则出现了37 组数据误诊断。这表明改进的SSA 优化RBF 神经网络后,有效增强了故障模型的分类预测能力,增加了麻雀种群的多样性,在区域搜索过程中收敛速度和适应度均得到了一定提升,因此可更准确地对光伏阵列故障进行诊断和预测。
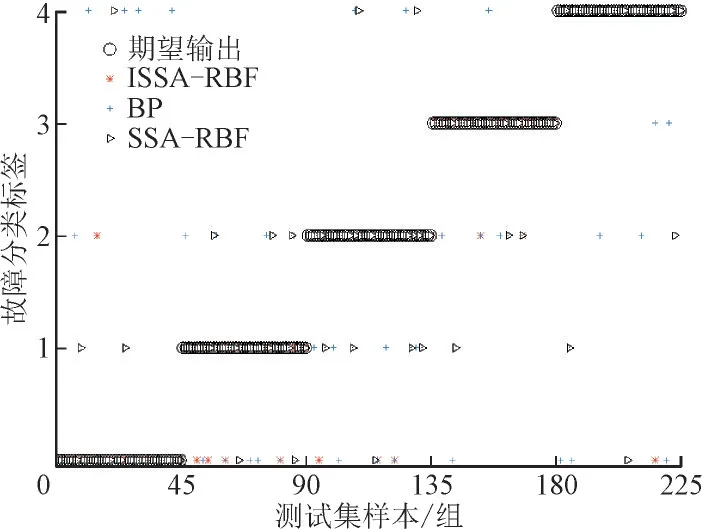
图7 测试集输出结果Fig.7 Output results of testing set
4 结论
针对光伏阵列故障难以被准确高效地诊断和分类问题,利用ISSA-RBF 神经网络模型对光伏阵列的组件进行故障诊断,得到如下结论:
1)ISSA 具有更强的寻优能力和更快的收敛速度,可有效对光伏阵列故障进行诊断,而不受模型其他参数影响。
2)相较于传统BP 模型和SSA-RBF 模型,ISSARBF 模型可以更迅速准确识别出光伏阵列的各类故障,在故障诊断效率和精度上有更明显的优势。
3)利用优化后的人工神经网络,建立的基于数据驱动的诊断模型,在训练样本充足的情况下能够有效解决光伏阵列组件故障诊断和分类问题。
