面向五轴数控加工仿真的机床运动位姿算法研究*
2023-03-16张越新凯丁国富
江 磊,张越新凯,梁 彬,丁国富
(西南交通大学,成都 610031)
数控加工仿真技术依赖于多种先进技术的交叉集成,通过计算机技术与虚拟现实技术建立加工仿真环境,结合数控技术与运动算法实现仿真机床的运动控制。由于数控加工仿真技术可实现机床加工状态的预先分析与工艺优化,并且五轴数控加工由于刀具位姿和机床运动的动态可变,因此五轴数控机床加工仿真技术的应用需求愈加迫切。
数控加工仿真技术包括三维仿真引擎、模型切削算法以及机床运动位姿计算等。针对三维仿真引擎,现有的研究主要围绕于Dexel表达法[1–2]、离散矢量求交法[3]、三角面片离散法[4]等仿真引擎算法展开,并成功搭建了图形学仿真环境。围绕模型切削算法,目前的研究主要针对布尔运算[5]、四叉树表达法[6]、八叉树表达法[7]等,实现了对模型体的高精度切削仿真。而在机床运动位姿计算方面,Bohez[8]、彭健钧[9]、肖通[10]等对五轴数控机床刀具运动仿真算法进行了研究,采用刀具扫描体的方式表达刀具运动轨迹,但未能对刀具仿真运动轨迹进行精确表达。
综上所述,数控加工仿真技术在三维仿真引擎与模型切削算法方面已形成较为完整的技术体系,但在机床运动位姿计算上还存在精度不足,如未考虑数控系统指令模式、加减速控制以及机床几何误差等约束条件。针对上述问题,本文基于五轴机床拓扑结构,重点考虑仿真空间中对于刀具运动轨迹密化计算与时间标记计算,并引入五轴数控机床运动轴几何误差参数,研究机床仿真模型实际位姿变换矩阵,保证机床仿真运动过程的准确性。
1 五轴数控机床仿真运动位姿计算流程
五轴数控机床仿真运动位姿计算方法主要用于对机床仿真运动过程的精确控制,其实现需要借助于对机床仿真拓扑结构定义、刀具位姿仿真密化计算与机床部件运动位姿计算。计算流程如图1所示。

图1 五轴数控机床仿真运动位姿计算流程Fig.1 Calculation flow of simulation movement position and attitude of five-axis CNC machine tool
(1)五轴数控机床仿真拓扑结构定义。
五轴数控机床运动结构可视为3个平动进给轴与2个转动进给轴的串联运动形式,共同实现刀具相对工件的位姿变化。为了实现仿真机床建模,将机床运动轴定义为运动节点和与之固联的几何模型,以及依附于其节点坐标系、模型坐标系、编程坐标系等。
(2)基于数控系统的刀具位姿仿真密化。
为了实现基于NC程序驱动的加工仿真过程,需要按照机床数控系统规则,从NC程序中提取机床运动数据。但是,目前NC程序段中的运动数据均为低密度的离散数据,若直接使用不仅将导致无法形成连续的仿真运动过程,而且运动轨迹与真实机床运动过程存在较大的偏差。因此,需要将机床运动数据转换为刀具位姿数据,并进行仿真密化计算、时间标记计算与转动轴转角计算,从而获得较为平滑的机床模型运动数据。
(3)基于仿真坐标系的机床模型运动位姿计算。
以平滑后的机床模型运动数据与机床拓扑结构为基础,推导机床仿真运动传递关系,获得机床模型理论位姿计算方法,结合机床实际运动轴几何误差项,获得机床模型实际位姿计算方法。
2 五轴数控机床仿真拓扑结构定义
2.1 拓扑结构定义
数控机床运动系统是由夹具、工作台、床身、各进给轴、刀具等组成的具有精密运动控制的复杂机械系统[11]。由刚体的多体运动学理论可知,五轴数控机床的每个运动部件均可简化为对应的拓扑节点[12]。拓扑节点分为运动型与功能型(即主轴、刀具、夹具、毛坯、工件、床身等)两种,其中运动型拓扑节点可进一步分为平动型(即机床X、Y、Z平动轴)与转动型(即机床A、B、C转动轴)。在进行机床仿真运动位姿计算时,为了描述机床运动的层级传递关系,定义机床床身节点层次为0级,其余节点按联接关系依次进行层次编号,直到刀具和毛坯节点结束,形成机床床身到工件和机床床身到刀具的两条单向运动链。以拓扑结构为WYXZCAT的五轴数控机床为例,其拓扑结构如图2所示。
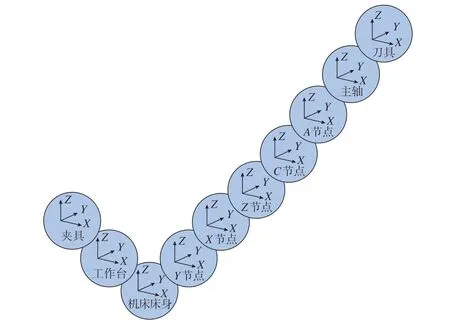
图2 五轴数控机床拓扑结构(以WYXZCAT为例)Fig.2 Topology structure of five-axis CNC machine tool (take WYXZCAT as an example)
2.2 机床模型定义
机床模型为数控机床部件在仿真空间中的几何映射[13],仿真机床通常使用三维模型导入(如stl、igs等格式的三维模型文件)或者参数化建模的方式构建。虽然实际上机床结构复杂,但是很多机床部件(如液压部件、机床外壳等)并没有直接参与加工仿真中的工件切除,可在不丢失仿真功能精度的条件下对机床模型进行简化。因此,可将数控机床仿真模型简化为运动轴模型、主轴模型、刀具模型、毛坯模型以及工作台模型等,模型实例如图3(a)所示。模型的位姿依附于对应的拓扑节点,并随节点位姿变化而变化。可以通过机床模型外表面的几何特征参数对加工过程进行碰撞干涉检测,模型表面特征如图3(b)所示。

图3 机床模型实例Fig.3 Example of machine tool model
2.3 机床仿真坐标系定义
按照右手直角笛卡尔坐标系的定义规则,定义下列坐标系,并通过坐标系的原点和坐标轴矢量表达其空间位姿关系。
(1)仿真坐标系定义。
为了在仿真空间中准确统一地描述机床运动,定义固定在仿真空间内的仿真坐标系SCS,定义点OSCS为其坐标系原点,矢量VX_SCS、VY_SCS、VZ_SCS表达其坐标轴方向。仿真坐标系位姿参数数据如表1所示。

表1 仿真坐标系位姿数据Table 1 Simulated coordinate system position and attitude data
(2)编程坐标系定义。
为了实现在NC驱动下的机床仿真运动与实际运动的一致性,满足机床加工工艺要求,定义编程坐标系PCS,其也为刀具位姿仿真密化计算的坐标基准。定义点OPCS为其坐标系原点,矢量VX_PCS、VY_PCS、VZ_PCS表达其坐标轴方向。编程坐标系位姿参数数据如表2所示。

表2 编程坐标系位姿数据(基于仿真坐标系)Table 2 Programmatic coordinate system position and attitude data (based on a simulated coordinate system)
(3)节点坐标系定义。
为了准确描述拓扑节点的坐标和方向,在节点上固联对应的节点坐标系NCS。以平动轴节点X为例,定义点OX_NCS为其坐标系原点,矢量VX_X_NCS、VX_Y_NCS、VX_Z_NCS表 达其坐标轴方向。平动轴节点X坐标系位姿参数数据如表3所示。其他节点坐标系定义与之类似,不再赘述。

表3 平动轴X节点坐标系位姿数据(基于仿真坐标系)Table 3 Position and attitude data of translation axis X node coordinate system (based on a simulated coordinate system)
(4)模型坐标系定义。
为了准确描述机床各模型的坐标和方向,在模型上固联对应的模型坐标系UCS。在同一节点下可包含多个模型,需对其进行编号。以平动轴节点X下的第n个模型为例,定义点OX_n_UCS为其坐标系原点,矢量VX_X_n_UCS、VY_X_n_UCS、VZ_X_n_UCS表达其坐标轴方向。平动轴节点第n个模型的模型坐标系位姿参数数据如表4所示。其他模型坐标系定义与之类似,不再赘述。

表4 平动轴X节点模型坐标系位姿数据(基于仿真坐标系)Table 4 Position and attitude data of translation axis X node model coordinate system(based on a simulated coordinate system)
3 基于数控系统的刀具轨迹仿真密化计算
不同数控系统的刀位轨迹插补算法存在差异,并且同一数控系统也存在不同插补模式。以西门子840D五轴数控系统为例,其G01指令存在线性插补ORIAXES、大圆插补ORIVECT、锥面插补ORICONCW 3种模式。为了确保机床仿真运动的准确性,需在NC程序离散的位姿数据基础上,对不同数控运动指令的刀具位姿进行密化。本文以G01指令的大圆插补模式为例,说明刀具轨迹仿真密化的计算流程。
3.1 刀具轨迹仿真密化计算流程
刀具位姿仿真密化计算分为NC程序解析、密化次数计算、刀具轨迹仿真密化位姿计算增减内容、刀具轨迹仿真密化时间标记计算与机床转动轴转角计算5个步骤,其流程如图4所示。

图4 刀具位姿仿真密化计算流程Fig.4 Tool position and attitude simulation densification calculation process
(1)NC程序解析。
根据西门子840D数控系统定义,NC程序的指令包括各种功能字符与运动数据。由于仿真密化计算仅对NC程序中的运动数据进行处理,故需对运动数据进行提取,称该过程为NC程序解析。
(2)密化次数计算。
定义刀位点间的密化间距λ和刀轴间的密化转角φ。将密化位姿计算精度值作为输入项,对密化间距λ和密化转角φ进行等分,将两者等分次数进行比较,更大值即为密化次数q。
(3)刀具轨迹仿真密化位姿计算。
通过机床多体运动学计算方式,将NC运动数据转变为刀轴矢量数据,并在此基础上进行刀位坐标和刀轴矢量的密化计算,得到密化后的刀具位姿数据。
(4)刀具轨迹仿真密化时间标记计算。
通过S型加减速控制对密化后的刀具位姿数据进行运动规划,建立密化后运动数据与运动时间的关系,获得刀具轨迹仿真密化时间标记。
(5)机床转动轴转角计算。
将密化后的刀轴矢量通过机床多体运动学逆运算,得到密化后的刀轴矢量对应的机床转动轴转角。
3.2 刀具轨迹仿真密化位姿计算
在完成NC程序解析和密化次数计算的基础上,结合大圆插补ORIVECT所具备的扇形刀具轨迹特征,完成对刀轴矢量与刀尖点坐标的密化计算。
(1)刀轴矢量转换。
设NC程序解析得到的第m行程序的转角数据为Cm、Am,则该行程序转角数据的目标刀轴矢量为
(2)刀轴矢量与坐标密化计算。
根据第m行与第m–1行刀轴矢量VPCS_m、VPCS_m–1及密化次数q,可得到刀具位姿仿真密化过程中的刀轴矢量递增角度为
根据递增角度θ进行刀轴矢量密化计算,可得第m行NC程序运动数据的第t段刀轴矢量密化结果为
设NC程序解析得到的第m行与第m–1行程序的刀尖点数据为(Xm,Ym,Zm)与(Xm–1,Ym–1,Zm–1),得到密化后的第t段刀尖点坐标为
3.3 刀具轨迹仿真密化时间标记计算
不同的数控系统对于刀具轨迹控制,不仅包括刀具位姿控制,而且还包括刀具进给加减速控制。为了准确对刀具轨迹运动过程进行仿真,将根据数控系统的加减速控制策略,在刀具密化位姿计算的结果上完成对应的时间标记计算。S型加减速控制是一种数控系统比较常见的控制策略[14],本文以常用的S型加减速为例说明具体的计算过程。
将S型加减速简化为变加速段、匀速段、变减速段3个阶段。根据第m行NC程序起止刀具位姿数据,其在3个阶段的位移量与运动速度关系可表达为
式中,SPCS_m为第m行起止点的距离;SPCS_m_1、SPCS_m_2、SPCS_m_3为第m行密化后的变加速段、匀速段、变减速段的位移量;F为指令进给速度;vPCS_s为程序起始速度;vPCS_e为程序终止速度;TPCS_m_1、TPCS_m_2、TPCS_m_3为 第m行密化后的变加速段、匀速段、变减速段的运动时间。
进一步可得第m行密化后的刀具位姿在3个阶段所对应的整体运动时间为
式中,aPCS为仿真运动加速度。
定义刀具每段密化位姿在第m行的时间标记tPCS_m_t,根据刀具密化位姿在不同的加减速阶段,可得
4 基于仿真坐标系的机床模型位姿计算
4.1 机床模型理论位姿计算
为准确描述机床仿真运动,采用齐次坐标变换矩阵计算各节点相对初始状态的位姿变化量,其中平动轴节点运动变换矩阵如式(8)~(10)所示。
式中,SXPCS_m_t、SYPCS_m_t、SZPCS_m_t为第m行第t段密化后平动轴运动量;M为平移运动。转动轴节点运动变换矩阵如式(11)~(13)所示。
式中,APCS_m_t、BPCS_m_t、CPCS_m_t为第m行第t段密化后转动轴运动量;R为旋转运动。
根据节点的拓扑层级,借助节点运动变换矩阵表达各拓扑结构节点的位姿传递关系,可得机床模型理论位姿计算的运动变换矩阵,如表5所示。
4.2 考虑几何误差的机床模型实际位姿计算
为了进一步提高仿真机床运动与实际机床运动的一致性,在仿真机床模型理论位姿计算的基础上,引入实际机床几何误差项。参考五轴数控机床几何误差项的详细描述[15–17],定义机床运动型节点的误差矩阵分别TM(X)_e、TM(Y)_e、TM(Z)_e、TR(A)_e、TR(B)_e和TR(C)_e,根据机床模型理论位姿计算矩阵,可得仿真机床模型的实际位姿计算变换矩阵如表5所示。
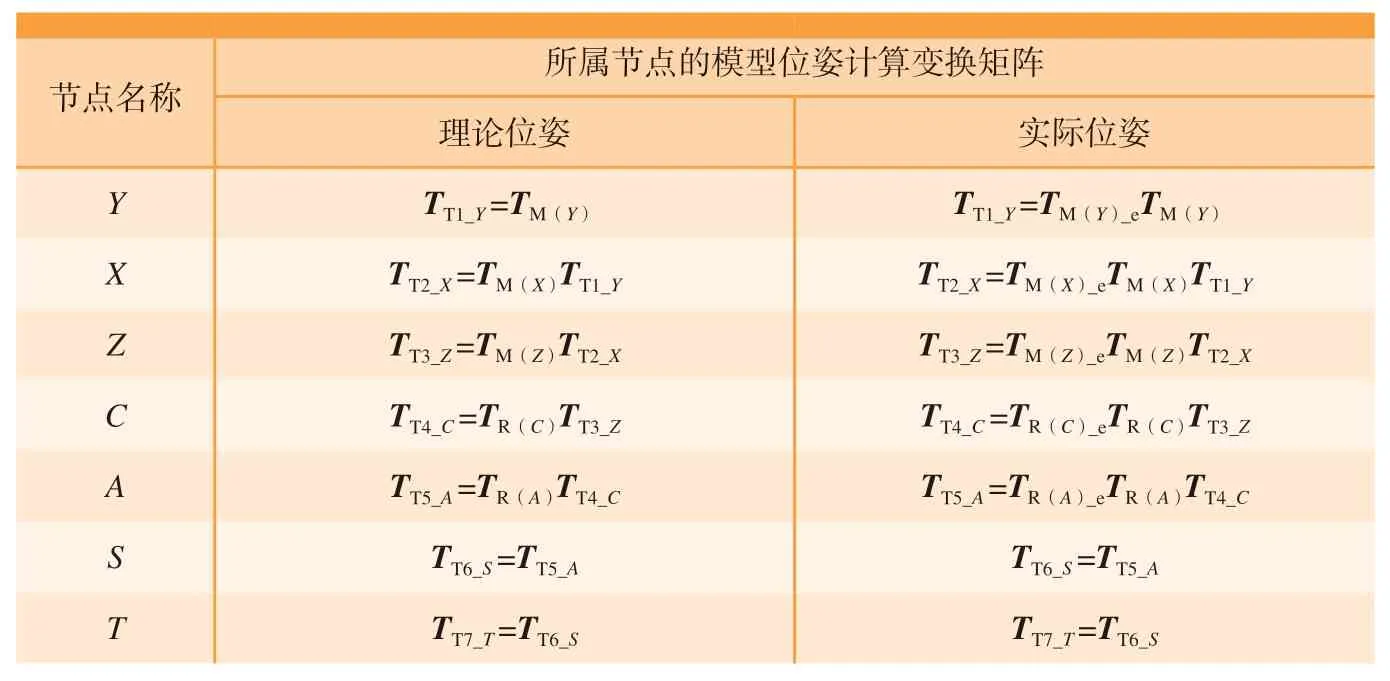
表5 机床模型理论位姿和实际位姿计算变换矩阵(以机床拓扑结构WYXZCAT为例)Table 5 Transformation matrix for calculating theoretical and actual position and attitude of machine tool model (take WYXZCAT as an example for machine tool topology)
5 应用验证
本文以拓扑结构为WYXZCAT的大型龙门式五轴数控机床为例进行仿真验证。为了简化节点建模过程,各节点坐标系坐标轴矢量均与仿真坐标系相同,如表6所示。

表6 调整后的机床节点坐标系位姿参数(基于仿真坐标系)Table 6 Adjusted position and attitude parameters of machine tool node coordinate system(based on simulation coordinate system)
为了简化模型建模过程,实例中的各节点只附属1个模型。根据机床的具体结构关系,对各模型坐标系进行了调整。调整后的机床模型位姿参数如表7所示。模型位姿调整实例如图5所示。
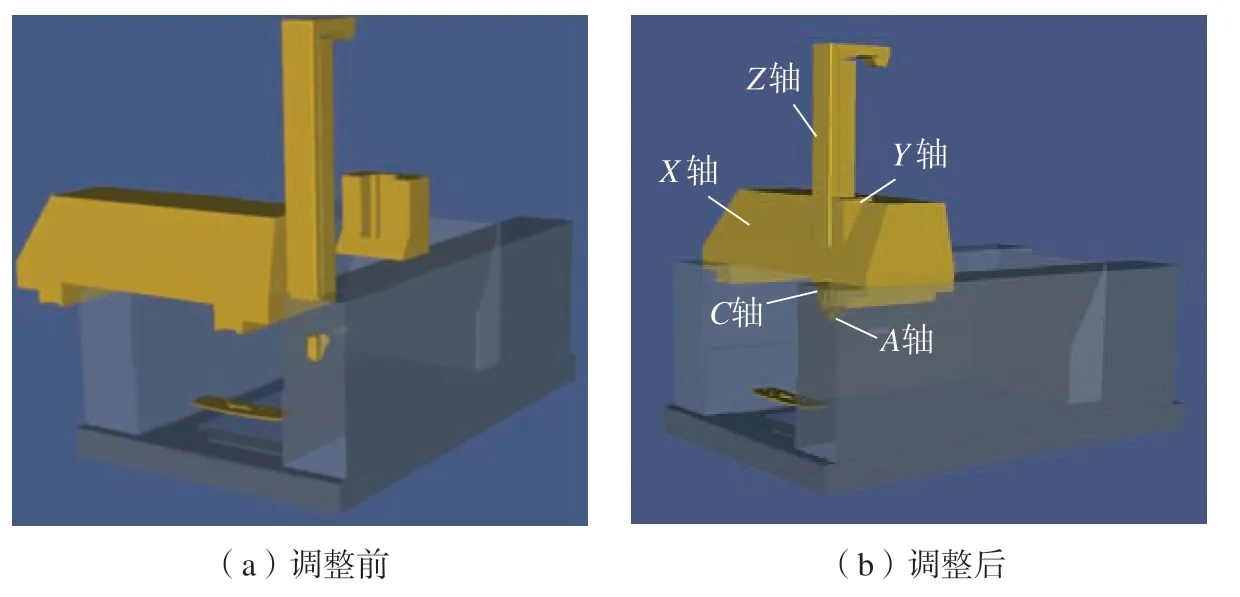
图5 模型坐标系位姿调整前后对比Fig.5 Position and attitude adjustment example of model coordinate system
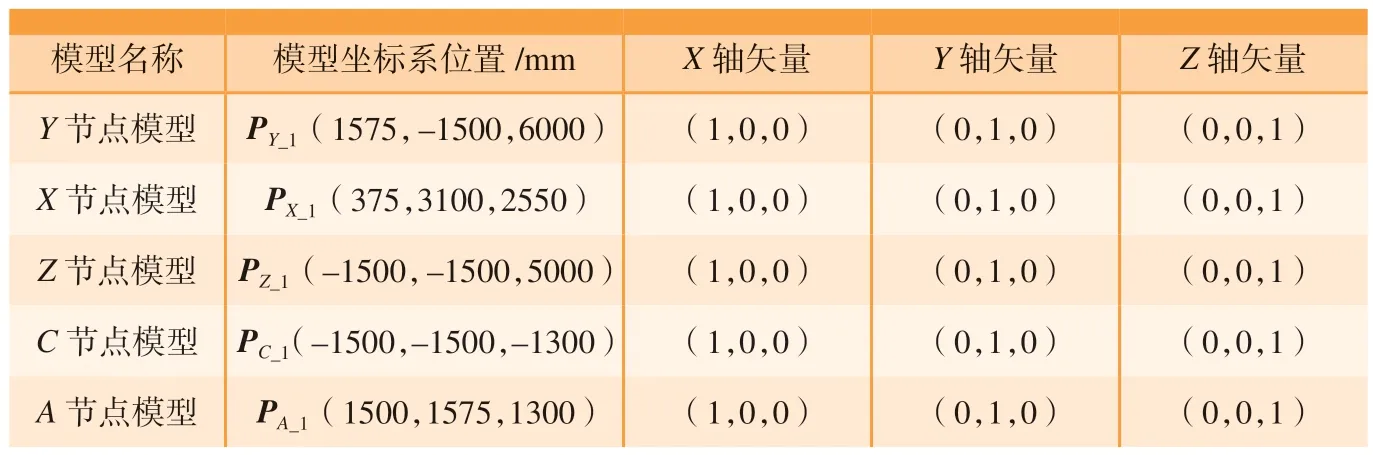
表7 调整后的机床模型坐标系位姿数据Table 7 Adjusted position and attitude data of machine tool model coordinate system
对某NC程序进行解析,程序部分示例如图6所示。

图6 NC程序示例(部分)Fig.6 NC program example (part)
提取NC程序中未密化的仿真运动数据,进行刀轴矢量转换与密化次数计算,获得密化次数q为100次,进行刀具轨迹位姿仿真密化计算,密化结果如图7所示。

图7 密化后刀具位姿数据(部分)Fig.7 Tool position and attitude data after densification (part)
设定进给速度F为1000 mm/min,程序起始速度vPCS_s与程序终止速度vPCS_e为0,仿真运动加速度aPCS为500 mm/s2,并进行仿真密化时间标记计算与转动轴转角计算,其计算结果如图8所示。

图8 密化后运动数据(部分)Fig.8 Motion position and attitude after densification (part)
基于密化后的机床仿真运动数据,结合表5中机床模型理论位姿计算方法,得到机床模型理论位姿数据如表8所示。
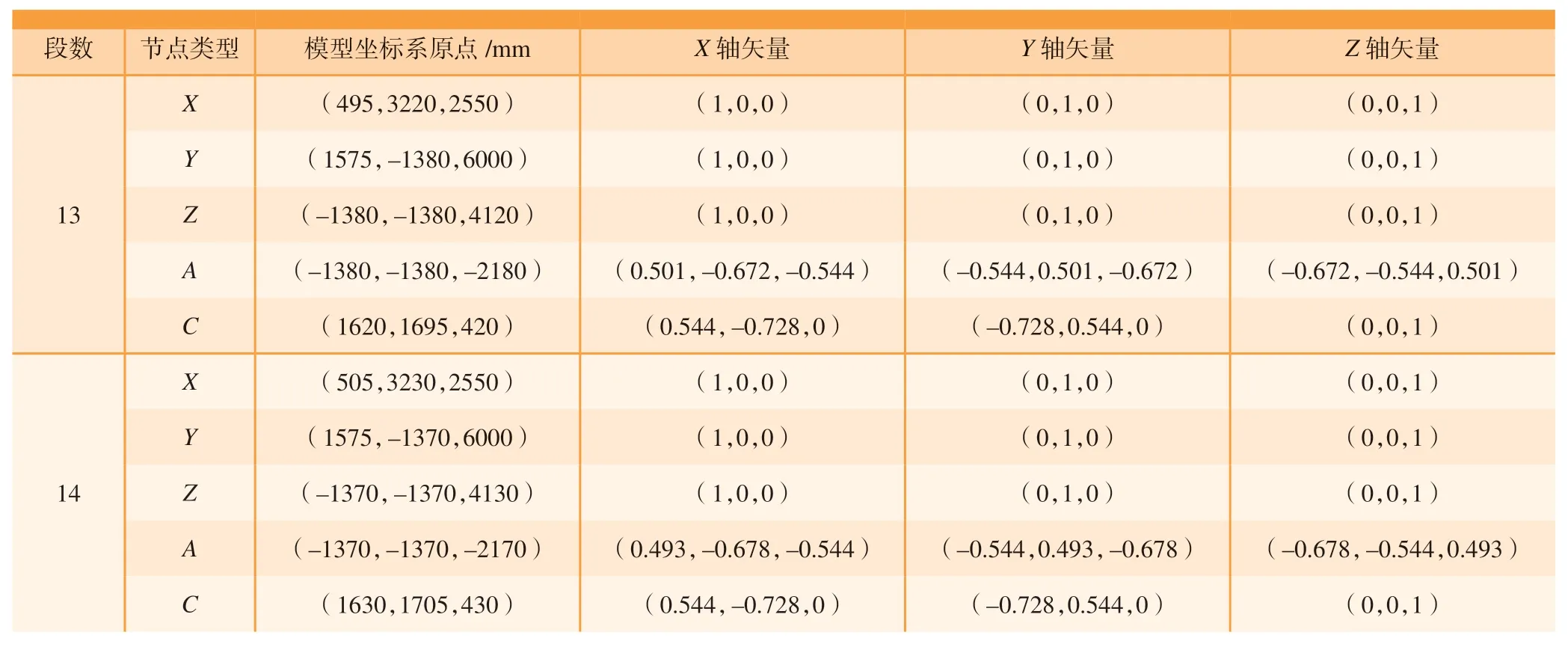
表8 机床模型理论位姿数据(NC程序第7行局部密化段)Table 8 Theoretical position and attitude data of machine tool model (local densification section in line 7 of NC program)
依据所测量的五轴数控机床运动轴几何误差数据,结合机床模型实际位姿变换矩阵,可得到机床模型实际位姿数据,如表9所示。

表9 机床模型实际位姿数据(NC程序第7行局部密化段)Table 9 Actual position and attitude data of machine tool model (local densification section in line 7 of NC program)
根据机床模型实际位姿数据,可得到机床仿真运动过程,如图9所示。
6 结论
本文研究了基于五轴数控机床仿真拓扑结构定义、刀具位姿仿真密化计算、刀具轨迹仿真密化时间标记计算与考虑五轴数控机床几何误差的机床模型位姿计算,得到了如下结论。
(1)针对五轴数控机床仿真拓扑结构定义了节点、机床模型与机床仿真坐标系,并对机床仿真运动位姿表达的相关参数进行了定义。
(2)针对刀具位姿仿真密化的计算方法,对数控系统指令模式、密化次数、矢量转换、刀轴矢量密化、刀位坐标密化的计算方式进行了阐述,保证了数控系统指令执行与机床仿真运动的一致性。
(3)针对刀具轨迹仿真密化时间标记的计算方法,采用简化后的S型曲线加减速算法,对密化后的刀具位姿数据进行速度控制,通过建立时间标记,实现对机床仿真运动时间的精确控制。
(4)对机床模型的理论位姿计算方法进行阐述,在机床模型仿真运动过程中引入机床几何误差项,保证机床仿真运动与实际机床运动的误差一致性。
