时间域航空电磁激发极化参数三维反演研究

满开峰， 殷长春， 刘云鹤， 孙思源， 熊彬

1 中国科学院深圳先进技术研究院， 深圳 518055 2 吉林大学地球探测科学与技术学院， 长春 130026 3 深圳市自然资源和不动产评估发展研究中心(深圳市地质环境监测中心)， 深圳 518040 4 中国自然资源航空物探遥感中心， 北京 100083 5 桂林理工大学地球科学学院， 桂林 541006

0 引言

时间域航空电磁法较传统地面电磁法具有勘探效率高、成本低、无需地面人员接近等明显技术优势，特别适合于地形复杂以及人员难以接近的地区(如高山、沙漠、湖泊沼泽及森林覆盖区)进行大面积勘查，已在油气、矿产、地下水和地热资源等领域获得广泛应用 (殷长春等，2015).基于实电阻率模型的时间域航空电磁中心回线(或重叠回线)装置得到的观测数据理论上是一个不变号的衰减曲线.然而，实际勘探中时间域航空电磁中心回线(或重叠回线)装置晚期道响应中常出现符号反转现象(如图1所示).众多学者对这种现象开展了深入的研究，认为这种符号反转现象是由地下介质存在激发极化效应(Induced polarization，IP效应)引起的，并一致同意基于传统实电阻率模型的成像和反演方法无法对此类符号反转数据进行有效解释(Lee，1975, 1981；Raiche，1983；Lewis and Lee，1984；Hohmann and Newman，1990；Flores and Peralta-Ortega，2009).因此，对此类电磁数据进行反演时需要考虑激电效应的影响.为描述方便，下文提到的航空电磁系统均为中心回线(或重叠回线)装置.

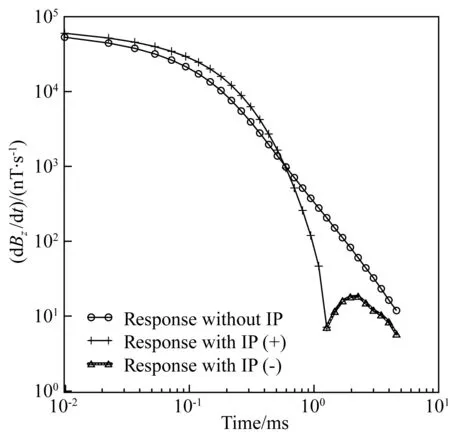
图1 时间域航空电磁响应(存在和不存在IP效应)Fig.1 Time-domain airborne EM responses (with IP and without IP)

电磁法勘探中激发极化参数反演的研究主要是近10年.Kratzer和Macnae(2012)提出了一种利用基函数拟合时间域航空电磁响应的方法.基于该方法时间域航空电磁数据可被分解成电磁感应和激发极化两部分，进而可以从激发极化数据中计算出视极化率.Chen等(2015)进一步提出了电磁响应分步提取技术：先利用基函数拟合提取出电磁感应产生的基本响应，然后根据基本响应和极化响应的关系再利用基函数拟合方法计算出极化响应，最后计算视极化率.随后，Macnae(2016)基于薄板模型设定基函数并提取出IP信息.此外，对于带激电效应的时间域电磁数据一维反演也取得了很好的进展.Yu等(2013)基于SVD方法对含IP效应的实测TEM数据进行反演，并从实测数据中分离出IP信息.Viezzoli等(2017)使用一维横向约束方法反演时间域航空电磁IP参数，结果表明当时间常数在一定约束范围内，该方法对电阻率和极化率有较好的求解能力.Lin等(2019)在一维横向约束基础上对反演做进一步改进，通过采用模型空间转换、在数据符号反转处增大误差、建立稳定的初始模型、设置合理的正则化因子等技术，获得了稳定的IP参数反演结果.缪佳佳等(2020)尝试利用Occam方法提取时间域航空电磁数据中心的激电信息，得到与真实模型较为接近的电阻率和极化率值.刘卫强等(2021)利用粒子群算法对各向异性激发极化进行反演，得到各地层在平行层理与垂直层理两个方向上的电阻率、充电率及时间常数.路俊涛等(2022)采用横向约束反演同时计算激电参数及层厚，增加约束条件从而改善多解性问题.此外，对于三维反演也有部分学者进行了尝试.Kang和Oldenburg(2016)对时间域航空电磁激发极化数据进行了三维反演.该方法将早期响应作为背景电阻率模型响应，并用总电磁响应减去背景电阻率模型响应近似得到极化响应后，再反演得到极化率.然而，该方法的反演精度受限于对背景电导率模型的准确估计和对极化响应的有效校正，实用性受到较大限制.

时间域航空电磁激发极化效应涉及电阻率，极化率，时间常数，频率相关系数等多个参数.由于激电参数之间灵敏度差异较大，时间域电磁法中激电参数反演存在严重的多解性，给反演结果的稳定性带来了极大的考验(缪佳佳等, 2020).另一方面，地下极化体的电阻率和极化率之间存在一定的相关关系，本文电磁数据反演中我们将这种相关性作为正则化项对反演进行约束，从而减小激电参数反演的多解性.统计中的Pearson相关系数可以描述两个变量的线性相关性，本文利用Pearson相关系数构建电阻率和极化率的相关关系，并在反演目标函数中引进由其构建的相关性约束项，从而实现基于Pearson相关性约束的时间域航空电磁数据反演.此外，实测数据反演中还需要考虑时间常数和频率相关系数，由于两者的灵敏度很小，与电阻率和极化率同步反演很难得到真实的参数值，本文采用深度学习方法预测时间常数和频率相关系数，通过给定时间常数和频率相关系数较小的约束范围，进一步减少反演多解性.我们将通过理论和实测数据验证本文反演算法的有效性.

1 三维正演计算

目前，用于描述岩矿石激电特性的模型有很多，使用较为广泛的是Pelton等(1978)提出的Cole-Cole模型，其表达形式为：

(1)

其中，ρ0表示零频电阻率；η为极化率，τ为时间常数，c为频率相关系数，i为虚数单位，ω为角频率.

假设时谐因子为eiω t，将总场分离为背景场和散射场，则由电磁场双旋度方程可得散射场满足如下偏微分方程(Newman and Alumbaugh, 1995)：

(2)

其中，μ0=4π×10-7H·m-1是自由空间磁导率，Ep是背景电场，Es是散射电场，σ(ω)是与频率相关的复电导率.

利用基于交错网格的有限差分方法(Alumbaugh et al., 1996)对式(2)进行离散，得到的线性方程组可表示为：

KEs=s,

(3)

其中，K为系数矩阵，s是右端项.我们采用拟残差法(QMR)(Siripunvaraporn et al.，2002)求解该线性方程组，得到电场值Es，并与一次场Ep相加得到总电场值E，进而由法拉第感应定律(式(4))可得到频率域的磁感应强度B.之后，我们利用殷长春等(2013)提出的反余弦变换法并与发射波形褶积，即可得到任意发射波形条件下时间域航空电磁响应.式(4)为：

(4)

2 基于Pearson相关性约束的三维电磁反演方法

统计学中的Pearson相关系数主要用来衡量两个变量之间的线性相关程度.其值介于-1和1之间.当两个变量的线性相关增强时，相关系数趋于1或-1.当两个变量的线性相关越弱时，相关系数越趋于0；若相关系数等于0，则表明两变量之间不相关.若存在两组长度相同的变量X={x1,x2,…,xN}、Y={y1,y2,…,yN}，则它们的Pearson相关系数可写为：

(5)

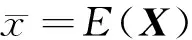
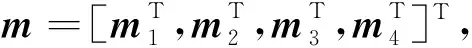
(6)

(7)

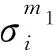
综合式(6)、(7)可以得到如下基于子域Pearson相关系数的相关性约束项，即：

(8)

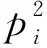
在使用梯度类反演算法对目标函数进行求解的过程中，需要计算目标函数的梯度.我们采用复合函数求导法则计算φs(m1,m2)对地下物性参数的导数，可得：

(9)

则每个子域内pi对物性参数m的导数可表示为：

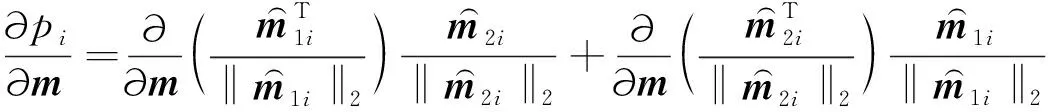
(10)

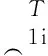
(11)

(12)

基于上面讨论的Pearson相关性约束，我们可以进一步讨论三维时间域航空电磁数据反演问题.为此，引入公式(8)的Pearson相关性约束项作为稳定泛函，构建如下正则化反演目标函数：

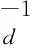
(13)

其中，d为观测数据，m0为初始模型参数，Cd为数据协方差矩阵，Cm为模型协方差矩阵.F(m)为正演算子，是一个非线性函数，需要对其进行线性化处理.为此，对F(m)进行泰勒展开，并忽略二阶及以上的高阶项可得：

F(m)=F(mk)+Jk(m-mk).

(14)

将式(14)代入式(13)，对m求导并化简后得到：

进而，令gk=0得到如下反演求解方程：

(16)

式(16)可利用共轭梯度法进行求解，得到模型更新量Δm.该向量指向目标函数的下降方向.我们采用Haber(2014)提出的线性搜索方式得到步长s，再利用公式mk+1=mk+sΔm获得每次迭代后新的模型参数.

3 激电参数预测

如上所述，激电参数之间灵敏度差异很大，特别是时间常数和频率相关系数的灵敏度远远小于电阻率和极化率，因此同步直接反演四个参数难度很大.本文先利用深度学习对激电参数进行估计，以此为基础给定时间常数和频率相关系数一个较小的约束范围后再反演电阻率和极化率，从而解决四个参数同步反演的多解性问题.

4)对于海底光缆频繁受损现状，在加强与海事、港监、边防等政府部门单位联络协调的基础上，利用现有的海缆监测平台增强实时监控能力，对禁锚海域展开全天候巡视，一旦发现情况，立即警告驱离，防止船只锚损事件重复发生。及时修复受损海底光缆，对承载有继电保护、图像监控和视频会议等业务的海底光缆提前做好相关的应急预案。

神经网络可以近似为如下非线性映射关系，即：

fθ∶X,H→Y，

(17)

其中，X是电磁响应数据，Y是激电参数模型.θ代表神经网络的参数，主要是指权重和偏置.f通常是一个复杂的非线性函数.我们可以通过神经网络来近似表示这种映射关系.

神经网络结构的构建通常依据经验设置.由于长短期记忆神经网络(LSTM)擅长于处理时间序列的数据，我们选择使用该神经网络.同时，为了提取数据特征，我们使用CNN+LSTM的网络模型，即在LSTM模型之前使用卷积神经网络CNN提取数据特征.在卷积层中，激活函数采用ReLU函数，在LSTM层中则采用tanh函数.网络收敛条件采用Early stopping方法.

我们可以通过训练集训练神经网络获得式(17)的映射关系.训练集主要包含神经网络的输入数据和输出数据(标签).输入数据为电磁响应，而输出数据对应地下激电参数.显然，我们的目标在于构建训练集来训练一个神经网络，使得向该神经网络输入一个电磁响应后，输出与该电磁相应对应的地下激电参数模型.通过在合理的参数范围内设计随机激电参数，进而使用一维正演软件 (Man et al., 2020)生成相应的电磁响应数据.在准备训练集过程中，需要对样本数据进行预处理.激电参数设计为均匀半空间模型，其中零频电阻率ρ0的取值范围为1～10000 Ωm，并按照对数域设计随机值.首先取[0,4]范围内的随机数R1，即R1∈[0,4]，则电阻率的取值为10R1.极化率范围设定为[0,1]，同样按照对数域取值，即假设对数极化率取值为10R2，R2∈[-4,0].同理，时间常数取值为10R3，R3∈[-5,-2].频率相关系数取值为10R4，R4∈[-2,0].

设计大小为200000的样本数据，包括训练集195000个和测试集5000个.在训练神经网络的过程中，我们使用minbatch gradient-descent方法对神经网络参数进行更新，主要过程是从训练集中选取一小部分样本子集(本文中batch的大小选取64)，通过梯度下降法使得该样本构成的代价函数值最小.本文使用的代价函数为Mean Absolute Error (MAE), 定义为预测值与期望值之间的平均绝对误差，即：

(18)

其中，K是矢量y的长度.式(18)可以通过反向传播BP算法求解.

4 理论模型反演

为了验证本文算法的有效性，我们首先设计理论模型进行反演测试.理论模型采用VTEM航空电磁系统.发射波形如图2所示.数值仿真时，我们假设发射线圈半径为17.5 m，匝数为2匝，发射电流峰值1000 A，发射磁矩峰值为9621100 Am2.接收机位于发射线框的中心，发射线框和接收机距离地表高度均为30 m.

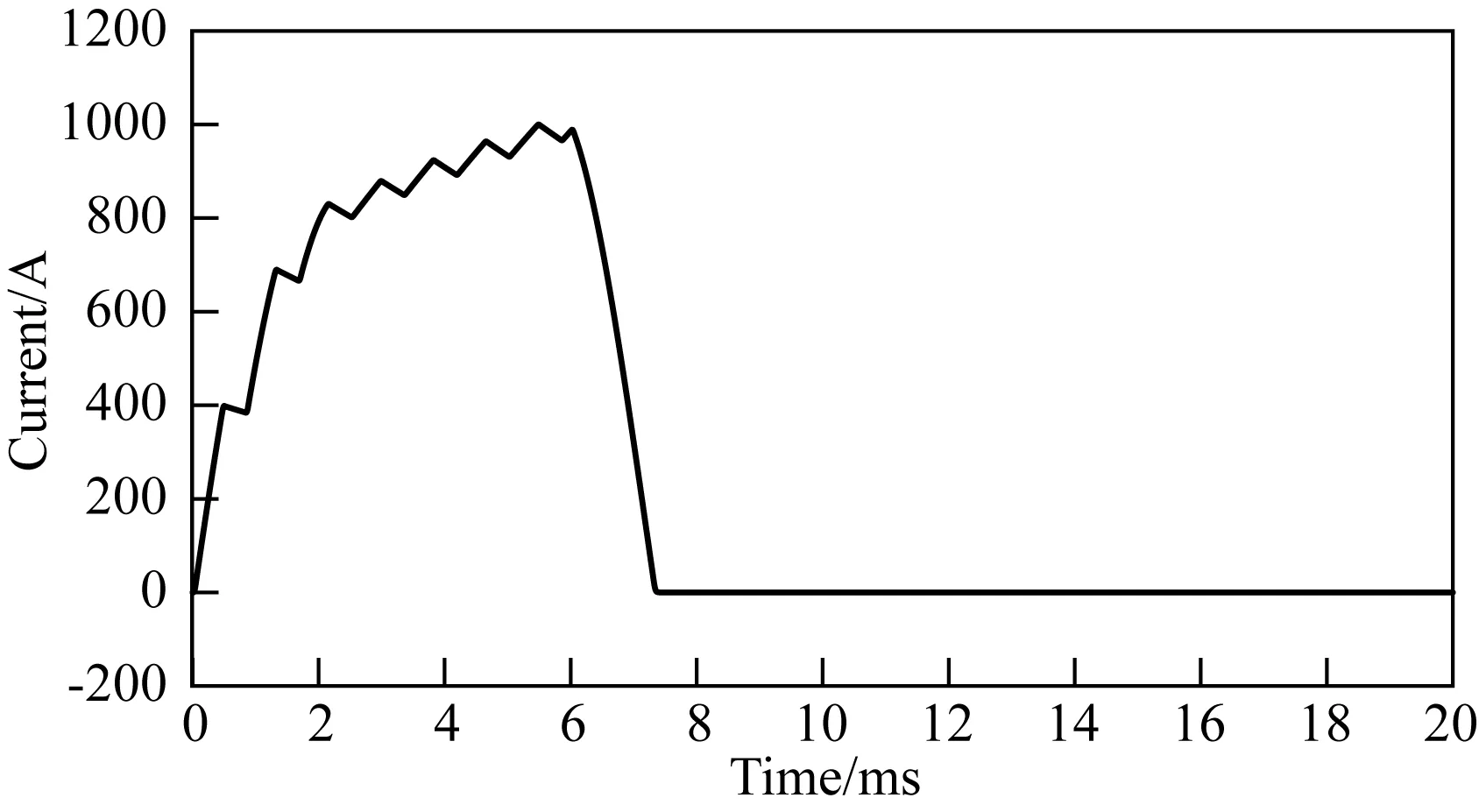
图2 VTEM系统发射波形Fig.2 Transmitting wave of VTEM system

4.1 电阻率和极化率的反演

电阻率和极化率是反映地下电性结构的重要信息，因此我们讨论如何从观测的电磁数据中反演得到地下介质的电阻率和极化率.由Cole-Cole模型可知，地下极化体包含电阻率、极化率、时间常数和频率相关系数四个参数，而得到的含有激电效应的电磁响应数据是由这四个参数共同作用的结果，因此实际上四个参数应该同步参与反演.考虑到四个激电参数的灵敏度差别很大，极化率的灵敏度小于电阻率，而时间常数和频率相关系数的灵敏度相对更小，因此本文先讨论赋予时间常数和频率相关系数真实值，并将其固定不变，再同步反演电阻率和极化率.由于电阻率和极化率灵敏度差异也较大，同步反演多解性也很严重，我们采用基于Pearson相关约束方法对电阻率和极化率施加相关性约束，以改善电阻率和极化率反演效果，减少多解性.

4.1.1 双棱柱异常体模型

下面首先设计一个双棱柱异常体模型，其xy和xz截面如图3所示.两个棱柱体的大小分别为150 m×180 m×46 m和150 m×180 m×55 m，埋深分别为30 m和37 m，两者的水平间距为120 m.两个棱柱体的电阻率均为10 Ωm，极化率为0.5，时间常数为0.001 s，频率相关系数为0.5.围岩的电阻率设计为100 Ωm，极化率为0.1，时间常数为0.0001 s，频率相关系数为0.1.我们采用30个断电时间道(off-time)计算时间域电磁响应并加入5%的随机噪声，将最终的合成数据作为待反演的理论数据.

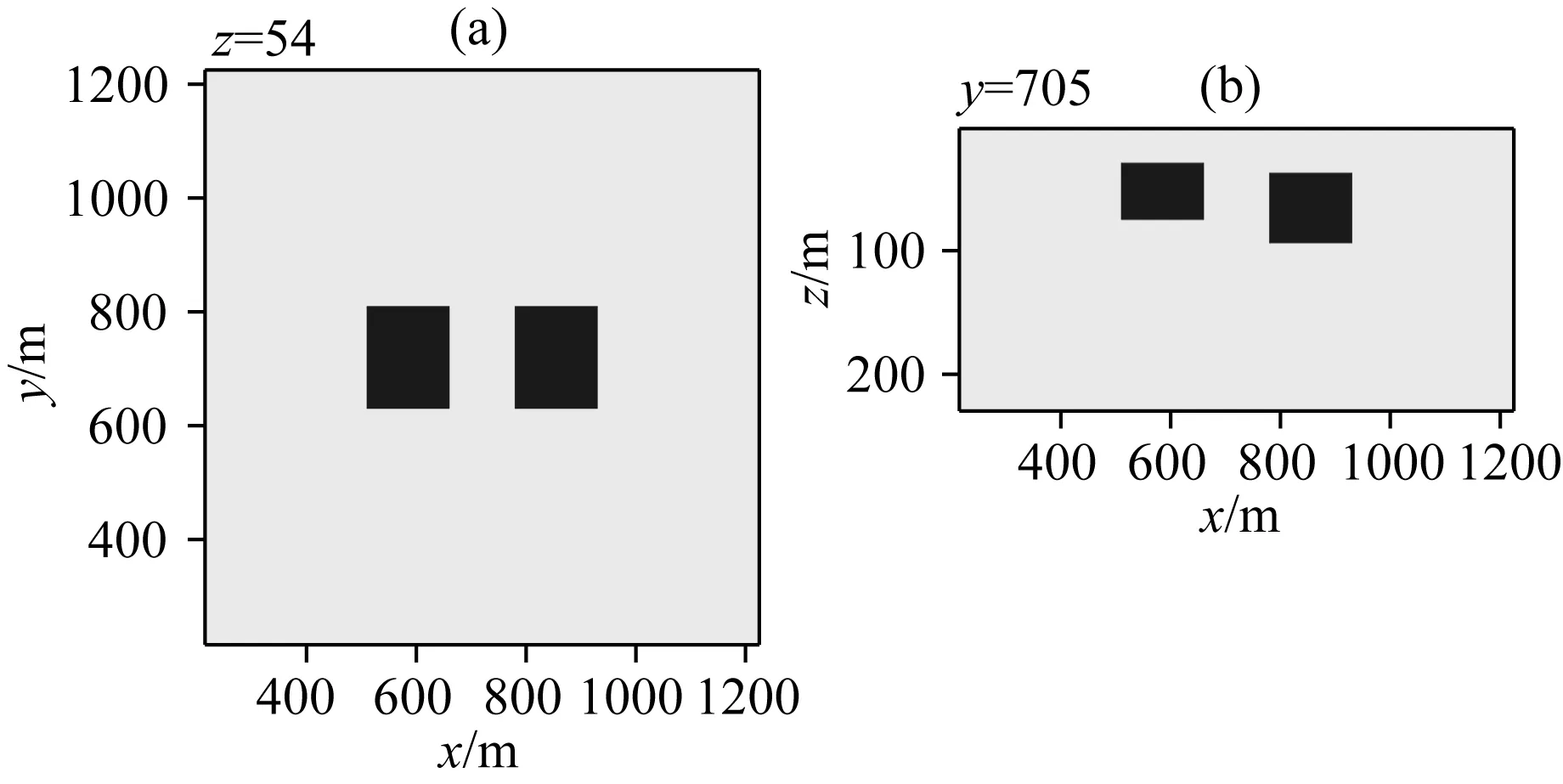
图3 双棱柱体模型示意图(a) z=54 m处xy剖面图； (b) y=705 m处xz剖面图.Fig.3 Schematic diagram of double prism model(a) xy section at z=54 m; (b) xz section at y=705 m.

首先对图3中的双棱柱异常体模型在固定时间常数和频率相关系数的条件下进行电阻率和极化率同步反演.图4和图5分别给出高斯-牛顿和基于Pearson相关约束的反演结果.从图4中可以看出，高斯-牛顿反演得到的两个异常体电阻率横向分布范围与真实模型基本一致，电阻率值与真实值较为接近，但两个异常体的电阻率纵向分布范围较大，两个异常体的深部边界均向下的延伸，左侧浅部异常体的地面位置出现了部分低阻假异常.对于极化率，两个异常体极化率的横向分布范围比真实模型稍大，而两个异常体在深部均有较大的延伸，在深部两个异常体连接在一起，难以区分.从图5中可以看出，基于Pearson相关约束反演得到的两个异常体电阻率横向分布范围和电阻率值均与真实模型基本一致，电阻率纵向分布范围也与真实模型较为接近，电阻率整体反演效果良好.对于极化率，两个异常体极化率横向分布范围与真实模型基本一致，而纵向分布范围稍大，有一定纵向延伸.

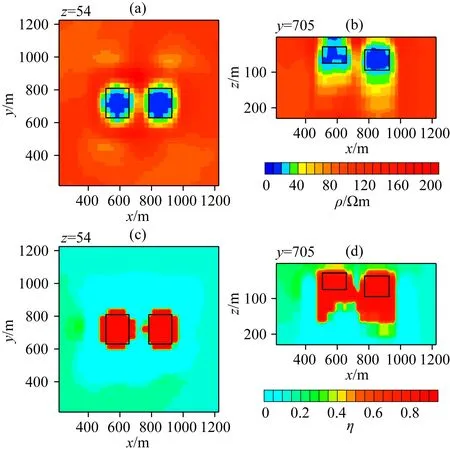
图4 高斯-牛顿法双棱柱模型电阻率和极化率反演结果Fig.4 Inversion results of resistivity and chargeability of double prism model by Gauss Newton method

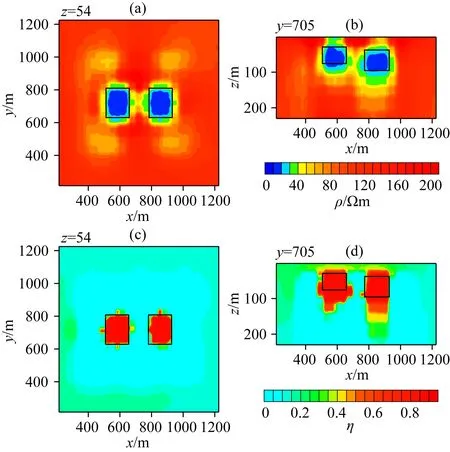
图5 Pearson相关约束双棱柱模型电阻率和极化率反演结果Fig.5 Inversion results of resistivity and chargeability of double prism model by Pearson correlation constrained method

对比两种反演方法得到的电阻率和极化率反演结果可以看出，两种方法得到的电阻率异常形态和电阻率与真实模型较为接近，电阻率反演结果总体比极化率的反演结果好.这主要是由于电阻率的灵敏度比极化率的灵敏度大很多，从而使得同步反演两个参数时电阻率较为灵敏，容易得到好的反演结果.对比高斯-牛顿和基于Pearson相关约束的电阻率和极化率的反演结果可以看出，基于Pearson相关约束的反演结果明显好于高斯-牛顿的反演结果，尤其是极化率的反演，高斯-牛顿反演不能在深部区分两个异常体，而基于Pearson相关约束反演得到的异常体在深部能够得到区分.这主要是由于基于Pearson相关约束反演考虑电阻率和极化率的相关性，减少了极化率反演的多解性.

4.1.2 拱形异常体模型

为进一步验证Pearson相关约束反演的效果，我们对图6中的拱形异常体模型进行反演试算.拱形异常体上顶面的水平方向大小为90 m×240 m，上顶面埋深为30 m，中部下低面的深度为60 m，左右两端下底面深度为120 m.异常体沿y方向的延伸长度均为240 m.拱形异常体的电阻率为10 Ωm，极化率为0.5，时间常数为0.001 s，频率相关系数为0.5.围岩的电阻率为100 Ωm，极化率为0.1，时间常数为0.0001 s，频率相关系数为0.1.对拱形模型进行正演计算，将生成的正演响应加入5%的随机噪声，最终合成的数据作为待反演的理论响应数据.

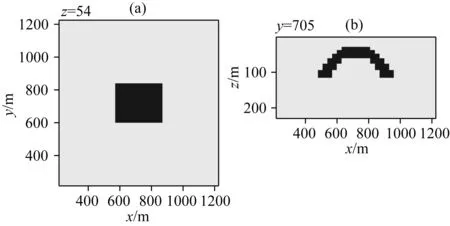
图6 拱形模型示意图(a) z=54 m位置xy切片； (b) y=705 m位置xz切片.Fig.6 Schematic diagram of arch model(a) xy section at z=54 m; (b) xz section at y=705 m.

图7和图8分别给出高斯-牛顿和基于Pearson相关约束的电阻率和极化率反演结果，其中黑色实线框为真实模型的位置.从图7中可以看出，高斯-牛顿反演得到的拱形异常体电阻率横向分布范围与真实模型基本一致，而拱形异常体的电阻率纵向分布与真实模型有一定的差异，左右两端下底面相对真实模型均呈现向下延伸，而拱形异常体上顶面上方出现低阻假异常.对于极化率，拱形异常体极化率的横向分布范围比真实模型大，中间和两端的下底面相比真实模型均有较大的延伸，左右两只连成一体.从图8可以看出，基于Pearson相关约束反演得到的拱形异常体电阻率和极化率横向分布范围与真实模型相当一致.特别是极化率呈现左右两只分开的形态，更接近真实模型分布特征.由此得出结论，基于Pearson相关约束的反演效果明显好于高斯-牛顿方法.

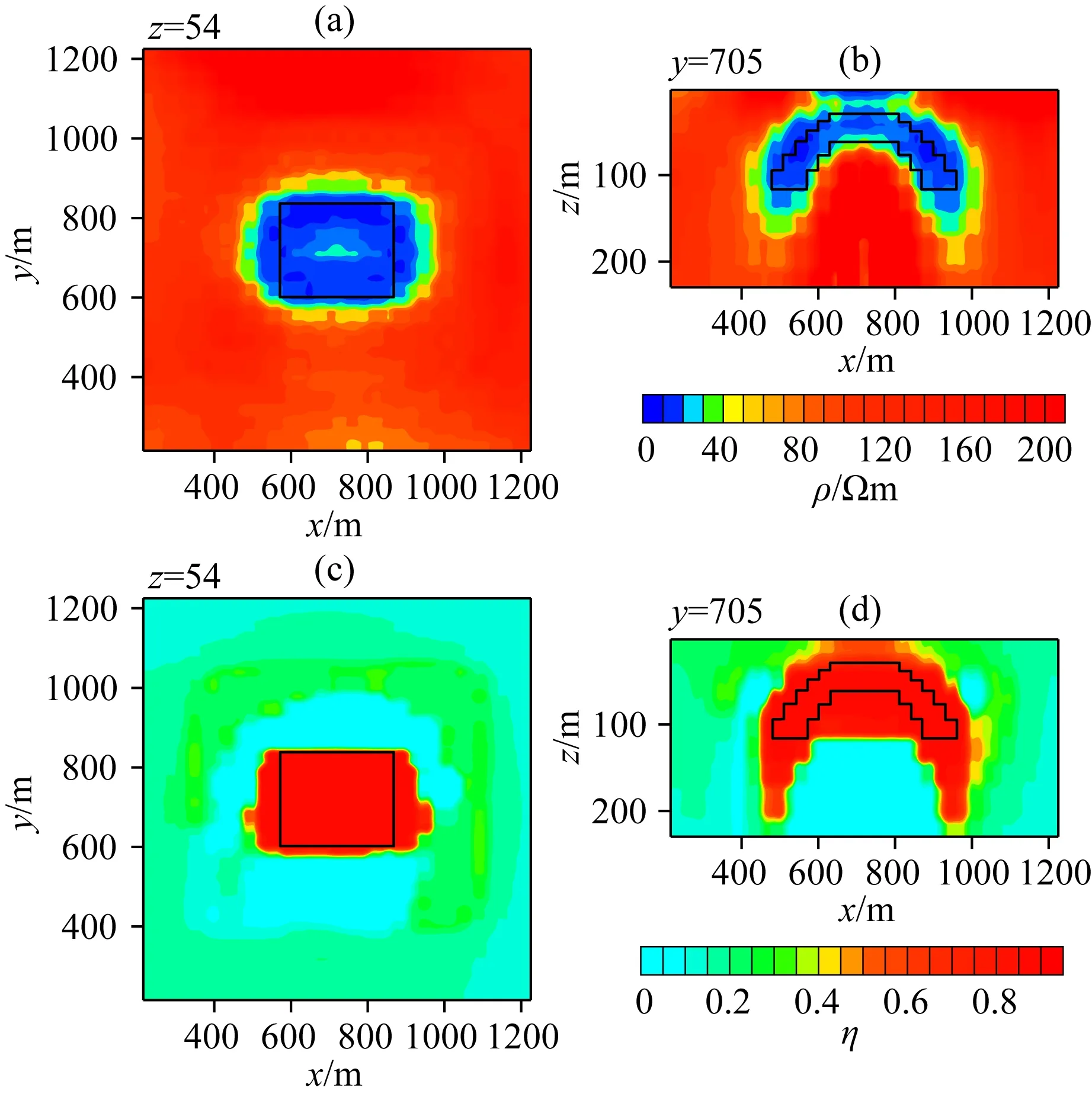
图7 高斯-牛顿法拱形模型电阻率和极化率反演结果Fig.7 Inversion results of resistivity and chargeability of arch model by Gauss Newton method

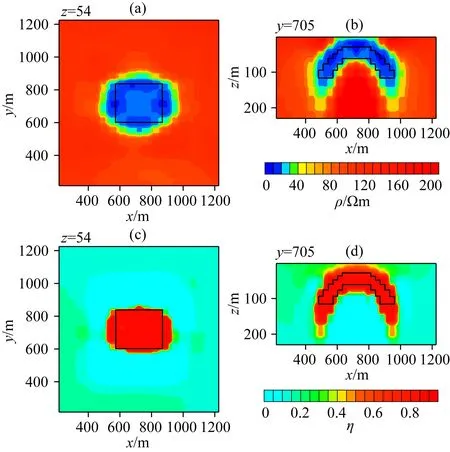
图8 Pearson相关约束拱形模型电阻率和极化率反演结果Fig.8 Inversion results of resistivity and chargeability of arch model by Pearson correlation constrained method

4.2 考虑四个激电参数的反演

为了实现四个激电参数的三维反演，本文提出深度学习估计激电参数和基于Pearson相关约束相结合的联合反演策略.为验证其有效性，我们利用深度学习对图6中拱形模型的时间常数和频率相关系数进行估算后，再进行电阻率和极化率反演.从图9给出的结果可以看出，利用该联合反演策略，拱形异常体电阻率和极化率形态与真实模型基本一致，但纵向分布范围有所增大.这是由于时间常数和频率相关系数估算结果不精确造成的.将图9中的反演结果与图8进行对比发现，利用深度学习估算时间常数和频率相关系数后，电阻率和极化率反演结果与给定真实时间常数和频率相关系数的电阻率和极化率反演效果相当，仅在纵向分布上向下拓展.这种现象不难理解.事实上，由于机器学习无法对时间常数和频率相关系数进行精确估算，因此联合反演无法获得与使用真实模型参数时相同的反演结果.

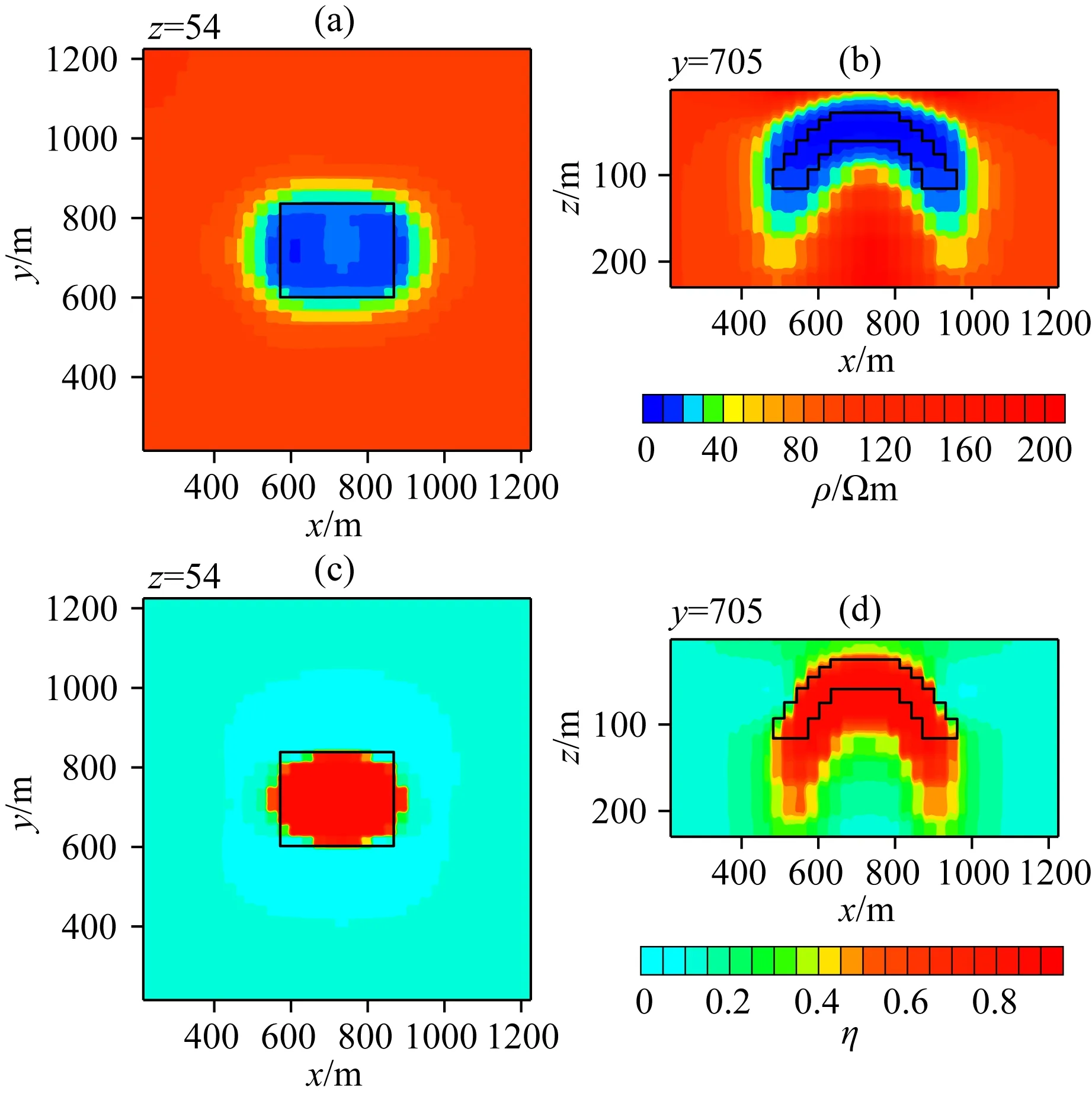
图9 利用深度学习估计时间常数和频率相关系数后拱形异常体电阻率和极化率反演结果Fig.9 Inversion results of resistivity and chargeability of arch model after estimating time constant and frequency exponent by depth learning method

5 实测数据反演

为了进一步测试本文反演策略的有效性，我们对澳大利亚马斯格雷夫省北部实测数据进行反演.航空电磁采用SkyTEM系统.发射波形如图10所示，on-time为5 ms.发射线圈面积为337 m2，匝数12匝，最大发射磁矩为473000 Am2，发射基频25 Hz.发射和接收线圈高度约为45 m.图11中红线给出航空电磁测线位置.本文中我们选取测线L502201、L502301、L502501、L502601、L502701中Northing 702739.4～702939.4范围内的实测数据作为测试区，测试区位于图12中蓝色矩形位置，每条测线点距为100 m，测点间距为250 m，包含有25个off-time时间道.为简单起见，下面讨论中将它们简单标记为L1、L2、L3、L4和L5.

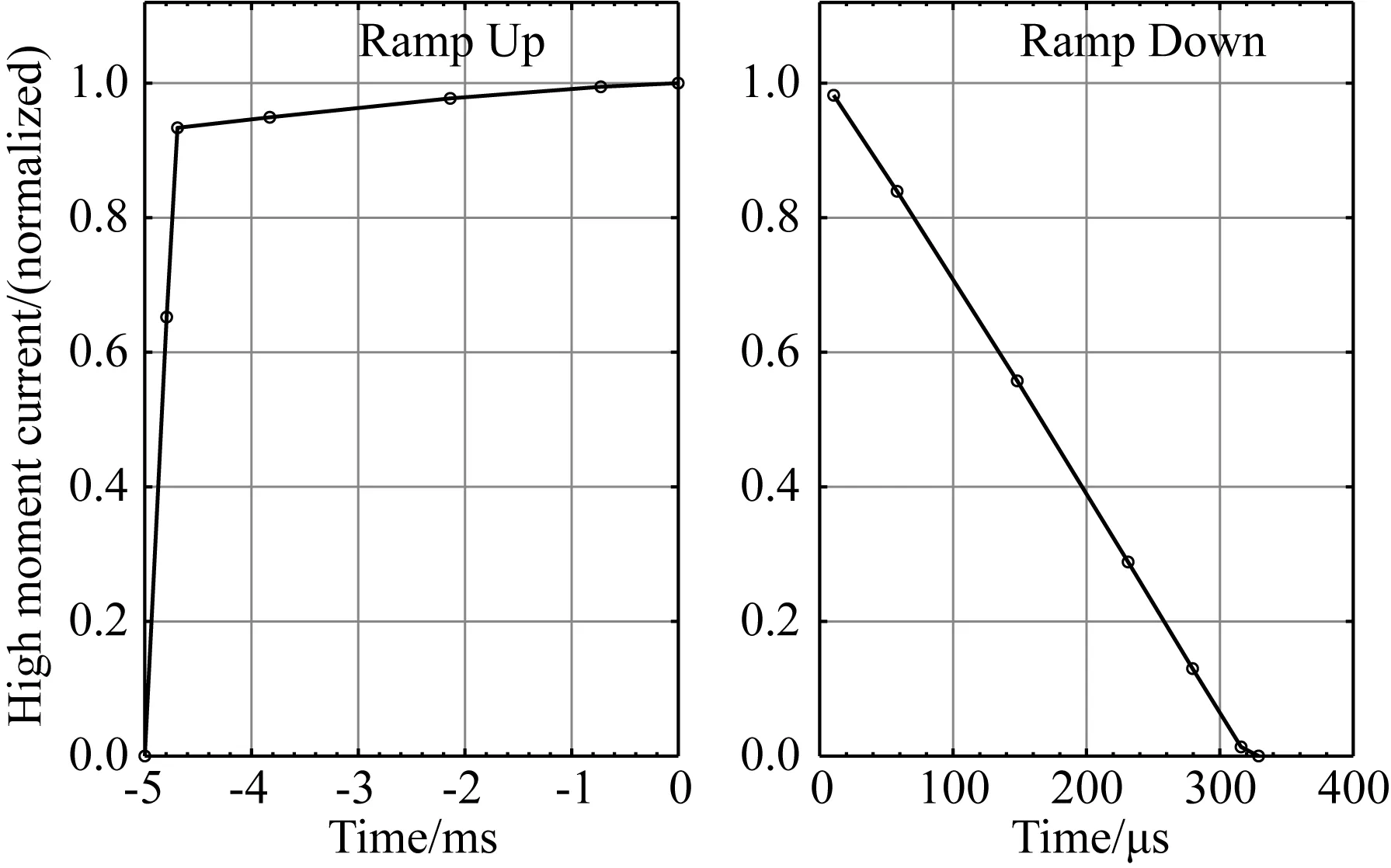
图10 SkyTEM系统发射波形Fig.10 Transmitting wave of SkyTEM system

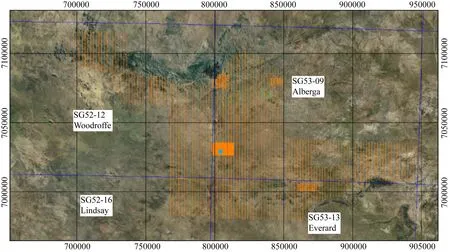
图11 澳大利亚马斯格雷夫省航空电磁测区示意图图片来自:https:∥ ecat.ga.gov.au/geonetwork/srv/chi/catalog.search#/metadata/110284.Fig.11 Schematic diagram of airborne electromagnetic survey area in Masgrave Province, Australia Picture from https:∥ecat.ga.gov.au/geonetwork/srv/chi/catalog.search#/metadata/110284.

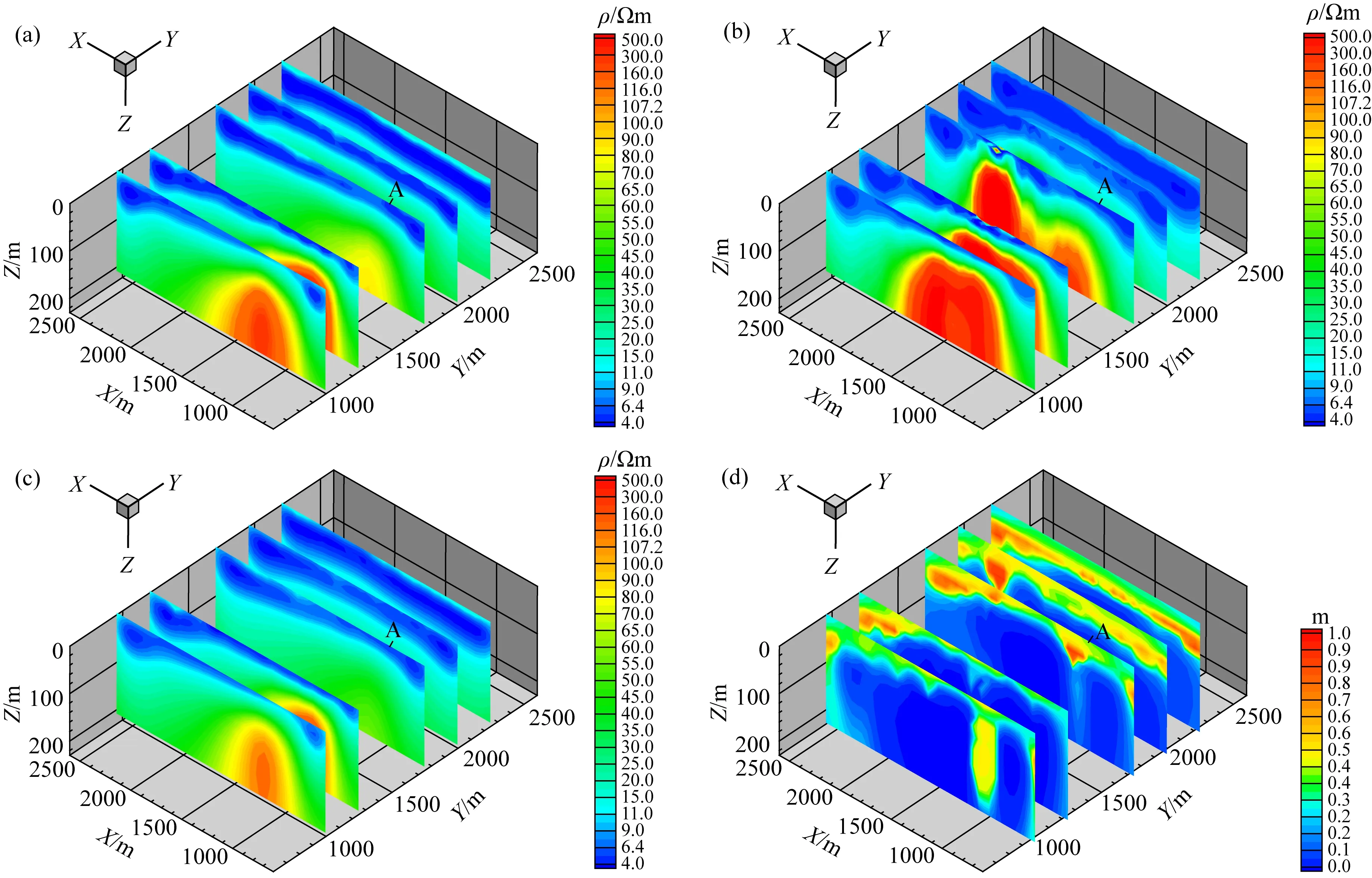
图12 澳大利亚马斯格雷夫省实测数据反演结果(a) 不考虑IP效应反演的电阻率结果(不包含负响应的19个时间道数据)； (b) 不考虑IP效应反演的电阻率结果(包含负响应的25个时间道数据)； (c) 考虑IP效应反演的电阻率结果(包含负响应的25个时间道数据); (d) 考虑IP效应反演的极化率结果(包含负响应的25个时间道数据).Fig.12 Inversion results of measured data in Musgrave Province, Australia (a) Resistivity inversion results without considering IP effect (excluding 19 time channel data with negative response); (b) Resistivity inversion results without considering IP effect (including 25 time channel data with negative response); (c) Resistivity inversion results considering IP effect (including 25 time channel data with negative response); (d) Chargeability inversion results considering IP effect (including 25 time channel data with negative response).

下面分别对不包含负响应的数据(19个时间道)进行不考虑IP效应的反演，对包含负响应的数据(取25个时间道)进行不考虑IP效应的反演和考虑IP效应的反演，反演结果如图12所示.图12a给出对19个时间道的正响应数据进行不考虑IP效应的反演结果，图中沿Y方向依次为测线L1～L5的电阻率反演剖面.从图可以看出，测线L2、L3、L4地下大致分为两层，浅部为低阻层，电阻率在4～10 Ωm，厚度5～100 m，深部为相对高阻层，电阻率为50～200 Ωm.测线L1中X=1000～1500 m处浅部低阻层消失，而地下存在一个高阻异常体.测线L5地下则表现为三层电性分布特征.图12b给出对包含负响应的25时间道数据在不考虑IP效应条件下的反演结果.与图12a相比，L4和L5测线的低阻层变厚，而测线L1、L2、L3均出现了电阻率为500 Ωm的高阻体.图12c给出对包含负响应的25个时间道数据，在考虑IP效应条件下的电阻率反演结果.从图可以看出，相比于图12a、b，测线L1、L2、L3、L4中低阻层更加连续，界面更加清晰，而测线L5的反演结果分为三层，与图12a反演结果一致.图12d给出对包含负响应的25个时间道数据进行考虑IP效应的极化率反演结果.从图可以看出，极化率表现为与电阻率分布特征类似的层状结构，高极化与低电阻率存在对应关系.综合图12c、d可以看出，测线L1、L2和L3均表现为浅部低阻高极化层，而深部为高阻低极化基底.测线L4和L5电性分为三层，中间层为低阻高极化层.

图13给出不考虑IP效应19个时间道数据反演、不考虑IP效应25个时间道数据反演和考虑IP效应25个时间道数据反演结果与实测数据的对比结果(以测线L3为例).从图可以看出，对不考虑IP效应19个时间道数据反演，理论和实测数据在19个时间上均拟合较好，而对不考虑IP效应25个时间道数据反演，理论和实测数据在x=1800～2000 m区间早期道没能很好地拟合，而晚期20～25时间道的数据无法得到拟合.对于考虑IP效应25个时间道数据反演，理论实测数据在早期道有较好的拟合，在包含负响应的晚期道也有一定程度的拟合.综上，对正响应数据进行不考虑IP效应的反演和对包含负响应数据进行不考虑IP效应反演均无法很好地拟合全时间道数据，而考虑IP效应的反演能够相对较好地拟合全时间道数据，说明考虑IP效应进行电磁数据反演的必要性.

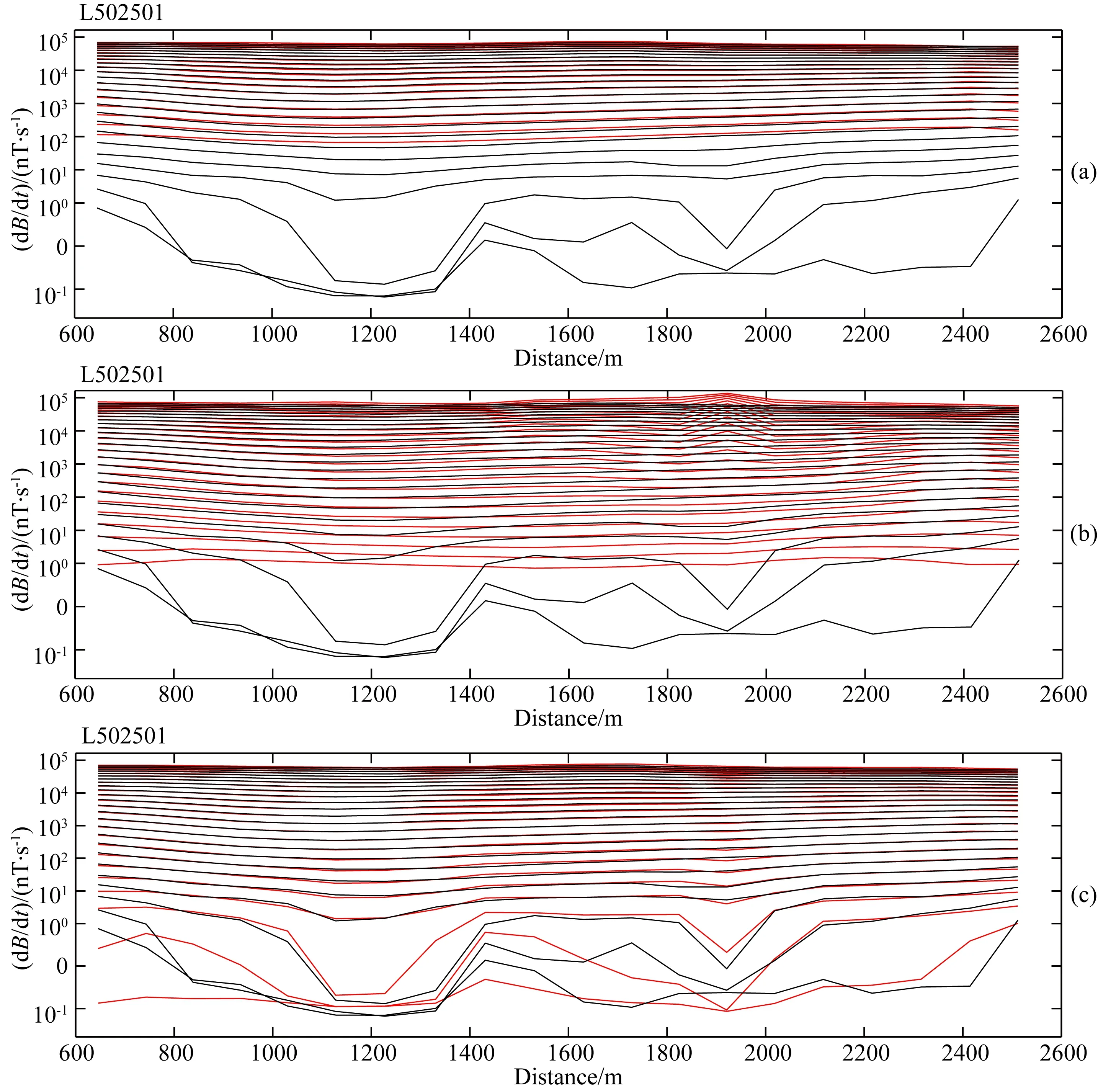
图13 (a) 不考虑IP效应19个时间道数据反演结果与实测数据对比； (b) 不考虑IP效应25个时间道数据反演结果与实测数据对比； (c) 考虑IP效应25个时间道数据反演结果与实测数据对比Fig.13 (a) Comparison of 19 time channels measured data and the results without considering IP effect; (b) Comparison of 25 time channels measured data and the results without considering IP effect; (c) Comparison of 25 time channels measured data and the results with considering IP effect

6 结论

本文将电阻率和极化率的Pearson相关性约束和深度学习预测激电参数成功应用于带激电效应的时间域航空电磁数据反演中，通过对理论和实测数据反演得出如下结论：

(1)高斯-牛顿法反演得到的极化率分布较为发散，而基于Pearson相关约束反演，由于考虑电阻率和极化率的相关性特征，得到的异常体极化率横向和纵向分布相对聚集，相比没有施加约束的高斯-牛顿法的反演结果更接近真实模型.电阻率反演结果也有一定的改善.

(2)本文提出的时间域航空电磁多激电参数联合反演是较为成功的反演策略.利用深度学习估计时间常数和频率相关系数后，基于估计的参数对电阻率和极化率进行相关约束反演，可以改善极化率反演效果.

(3)对不包含负响应数据进行不考虑IP效应的反演，对包含负响应数据进行不考虑IP效应的反演和考虑IP效应的反演结果表明，考虑IP效应反演的低阻层更加连续，界面更加清晰，数据拟合程度高，说明反演中考虑IP效应的必要性.

致谢感谢吉林大学电磁研究团队成员在本文准备过程中给予的帮助.感谢Geoscience Australia提供的实测航空电磁数据 (https:∥ecat.ga.gov.au/geonetwork/srv/chi/catalog. search#/metadata/110284).最后，对两位审稿人提出的建设性意见表示衷心感谢！