地面多分量地震数据P/S波分离的深度学习方法
2023-03-15黄河王腾飞程玖兵熊一能朱峰
黄河, 王腾飞, 程玖兵, 熊一能, 朱峰
1 页岩油气富集机理与有效开发国家重点实验室, 北京 100083 2 中国石化弹性波理论与探测技术重点实验室, 北京 100083 3 同济大学海洋与地球科学学院, 上海 200092
0 引言
多分量地震数据较完整地记录了地震波的三维矢量振动信息,有助于联合纵波(P)与横波(S)信号改善气云区、火成岩及盐下等复杂地质构造成像以及降低岩性区分、裂缝检测、储层预测与流体识别的多解性(李彦鹏和马在田,2000; Stewart et al.,2002;Hardage et al.,2011; 李向阳和王九拴,2016).在常规处理流程中,为了在速度建模与偏移成像中克服P与S波相互串扰,一般需先采用P/S分离技术将多分量地震数据分解为标量P波与S波记录(陶春辉和何樵登,1993;Van der Baan,2006),然后开展各自的速度分析和偏移成像处理(李录明和罗省贤,1998;许士勇和马在田,2002;芦俊等,2018).近年来,针对多分量地震数据反射走时层析和全波形反演问题,王腾飞(2017)和Xu等(2019)发现P/S分离数据或梯度预条件对降低非线性、压制参数耦合和提高反演收敛性也有很大帮助.
多分量数据P/S分离通常依据两种波模式的视速度或偏振(极化)特征差异,基于地震波传播理论(Dankbaar,1985;Wapenaar et al.,1990;Amundsen and Reitan,1995)或者采用信号处理方法(Esmersoy,1990;胡天跃等,2004)进行数据分离.前者除了依赖于表层介质弹性参数(Schalkwijk et al.,1999;Sun et al.,2004;Li et al.,2016;王晨龙,2017;Gu et al.,2022),还很难准确处理临界反射角之外的地震信号(Wang et al.,2002).后者无需提供近地表参数的先验信息,但受限于局部平面波出射假设,涉及的局部慢度和极化方向估计需要密集的炮检分布,且难以处理复杂的波场传播效应(Cho and Spencer,1992;Al-Anboori et al.,2005).无论是陆地还是海洋多分量地震数据处理,有效的P/S分离仍是一个尚未解决好的课题(Lu et al.,2017;刘学义等,2021;刘学义,2021).
多分量地震数据P/S分离可视为一类复杂的数据重构问题.近年来,人工智能方法在地震学领域受到极大关注,启发了一些学者依靠卷积神经网络强大的非线性表达与函数拟合能力,尝试建立不依赖于表层介质参数和局部平面波假设的P/S分离新方法.一方面,针对各向异性介质弹性波P/S模式解耦问题,基于偏振投影低秩近似算法(Cheng and Fomel,2014)构建的标签数据集,利用循环生成对抗网络模型(Kaur et al.,2019)或基于编码器-解码器的U-net网络模型(Huang et al.,2021),构建的深度学习方法可以有效降低波前快照P/S分离的计算成本.另一方面,Wei等(2020)提出了基于多任务学习的垂直地震剖面(VSP)数据P/S分离方法,Xiong等(2020)提出了基于U-net网络的地表多分量数据P/S分离方法.值得注意的是,这些监督学习方法需要大量标签数据用于训练网络模型.由于在实际应用场景下很难获得精度可靠,有广泛代表性的标签数据,它们都基于理论模型合成数据构建P/S分离训练样本.显然,理论模型与训练样本的代表性会直接影响网络的泛化性能,但相关的分析和讨论却不太充分.
本文根据地面多分量地震数据处理需要,基于编码器-解码器结构的卷积神经网络模型,提出一种稳健、实用的P/S分离方法.首先,将多分量地震记录P/S分离视为一个逐点预测非线性反问题,给出相应的深度学习方法原理.然后,重点论述理论模型与训练样本集的构建方式,并结合数值实验展示网络训练、验证和测试过程,揭示网络模型的泛化性能.最后讨论数据频率特征、炮检距范围以及噪声等因素对网络预测性能的影响.
1 基于U-net网络的P/S分离方法
多分量地震记录P/S波分离本质上是将观测数据按波型差异重新进行能量分配,属于点到点预测问题,可利用卷积神经网络强大的非线性表达能力建立相应的深度学习方法.在二维情况下,深层神经网络将地面地震记录的水平分量ux和垂直分量uz视为双通道输入数据,对空间-时间域每个样点预测其波型成分,最终输出独立的标量P波和S波地震数据,即:
(1)
其中OP和OS分别表示网络输出的P波与S波信号,f(·)代表卷积神经网络模型,θ为网络参数.这里采用的U-net是一种编码器-解码器结构的卷积神经网络(如图1),具有强大的非线性函数拟合与多尺度特征提取能力(Ronneberger et al.,2015).基本卷积单元含有两个卷积层,其中卷积核大小为3×3,步长为1,在每个卷积层后设置ReLU激活函数.图中N表示经过第一个基本卷积单元后的特征图数量.编码器部分包含四次下采样过程,通过步长为2的卷积降低特征图的空间分辨率,以提取输入数据更为抽象的特征.每次下采样后特征图数量将翻倍.解码器部分则对应四次上采样过程,通过步长为2的转置卷积增大特征图的空间分辨率,最终将其恢复至输入数据的大小.编码器与解码器之间通过跳层连接将相同分辨率的特征图沿通道方向进行拼接,从而实现不同尺度特征的融合.最终通过1×1的卷积操作得到两个通道的输出,分别对应分离后的标量P波与S波记录.
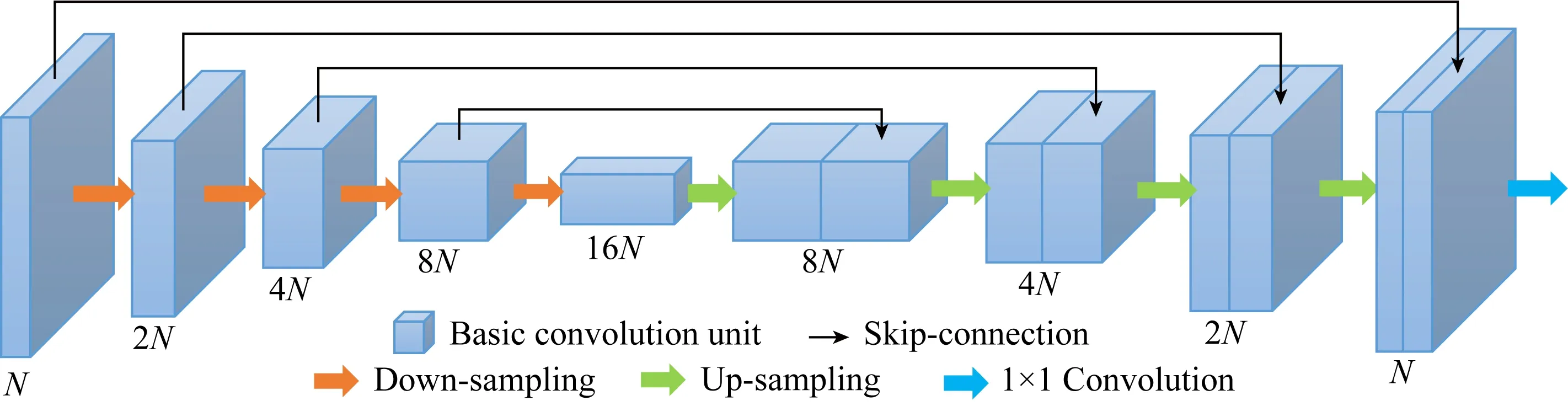
图1 面向P/S分离的U-net网络结构示意图Fig.1 The U-net architecture for P/S separation
神经网络训练是求解最优化问题的过程.这里采用L1范数定义网络训练的损失函数:
(2)
在每次迭代中,利用标签数据(uP,uS)和网络预测结果计算损失函数,然后通过反向传播算法求得损失函数关于网络参数的偏导数(泛函梯度),进而更新网络参数直至损失函数最小化.最终根据网络模型在验证集上的表现选取最优参数,用于后续的测试过程.
为了使网络模型能够适应任意尺寸的地震炮道集,我们在训练过程中将单炮数据随机裁剪为大小一致的数据块作为网络输入,而在验证和测试过程中通过滑动窗口的方式完成对整个炮道集的处理.这种方式能在一定程度上丰富训练样本并减少显存占用,从而更好地适应计算资源.
2 训练样本集
监督类深度学习方法通常需要大量的标签数据用于网络模型训练,以便合理地建立输入与输出之间复杂的非线性映射关系.这类方法对数据分布特征有较严格的要求,若目标数据与训练样本之间存在严重的特征不匹配,则网络在目标任务中一般难有较好的表现.此外,准确的标签数据能为网络训练提供精准的迭代优化拟合目标,使得网络提取出的映射关系更加可靠,预测结果更加可信.因此,对于P/S分离问题而言,训练样本的丰富性与标签数据的准确性对网络的性能与泛化能力十分重要.
构建丰富的训练样本需要考虑地下介质速度结构对波场传播与偏振特征的影响.从物理上看,表层介质速度直接影响到达检波器的P波和S波的出射与偏振方向,而中、深层速度结构则影响地面多分量地震记录的时距关系和振幅变化.在实际数据处理中,由于表层介质参数不易准确估计以及波场十分复杂,很难基于物理学原理或信号处理方法从多分量地震记录中分离出准确的P/S数据作为训练样本.因此,一种构建训练集的可行方案是基于理论模型合成多分量记录P/S分离结果.其优势在于:①便于仿真多种多样的地下弹性介质情况,在训练集中包含浅表与中、深层不同速度-密度结构对应的波场分离样本,提升训练集的丰富性和代表性,进而增强网络的泛化能力;②由于理论模型介质参数已知,可以通过亥姆霍兹分解理论计算精确解耦的P/S波数据,因此保证了标签数据的可靠性.由此看来,构建用于合成多分量记录的弹性介质模型是本文方法最基础、最关键的环节.
这里采用两个步骤建立训练所需要的样本数据库:首先,考虑实际地质情况的多样性和复杂性,构建大量具有典型构造特征和表层介质条件的弹性参数模型,形成理论模型样本库;然后,针对库中模型开展弹性波数值模拟,合成多分量地震记录,并基于亥姆霍兹分解得到精确解耦的P与S波记录,从而形成一整套适用于网络训练的标签数据集.
2.1 理论模型样本库
利用勘探地球物理协会(SEG)和欧洲地球科学家与工程师协会(EAGE)近30年来公开的大量地质和弹性参数模型,采用恰当的数据增广策略,借助弹性波数值模拟和精确解耦构建丰富的P/S分离标签数据集.以地质模型纵波速度为例,模型样本扩充的策略和步骤如下:
(1)基础模型增广.鉴于SEG和EAGE公开的Marmousi、Hess、Sigsbee、SEAM2D、BP等理论模型都有纵波速度数据,故通过仿射变换对所有纵波模型进行扩充,并从中随机裁剪出任意长宽比的小块作为样本库的基础模型.
(2)模型随机扰动.对基础模型中速度值施加随机的整体扰动,并通过缩放使所有模型宽度一致.然后再进行一次小幅度的仿射变换,使扰动后的速度模型深部结构符合地质意义且更加多样化.
(3)表层介质建模.为随机扰动后的速度模型添加厚度为h的表层介质,使其代表复杂多变的近地表速度结构.具体而言,先对扰动后模型顶面速度进行横向平滑,然后以此为基准按如下公式向上延拓以添加厚度为h的表层非均匀介质,即:
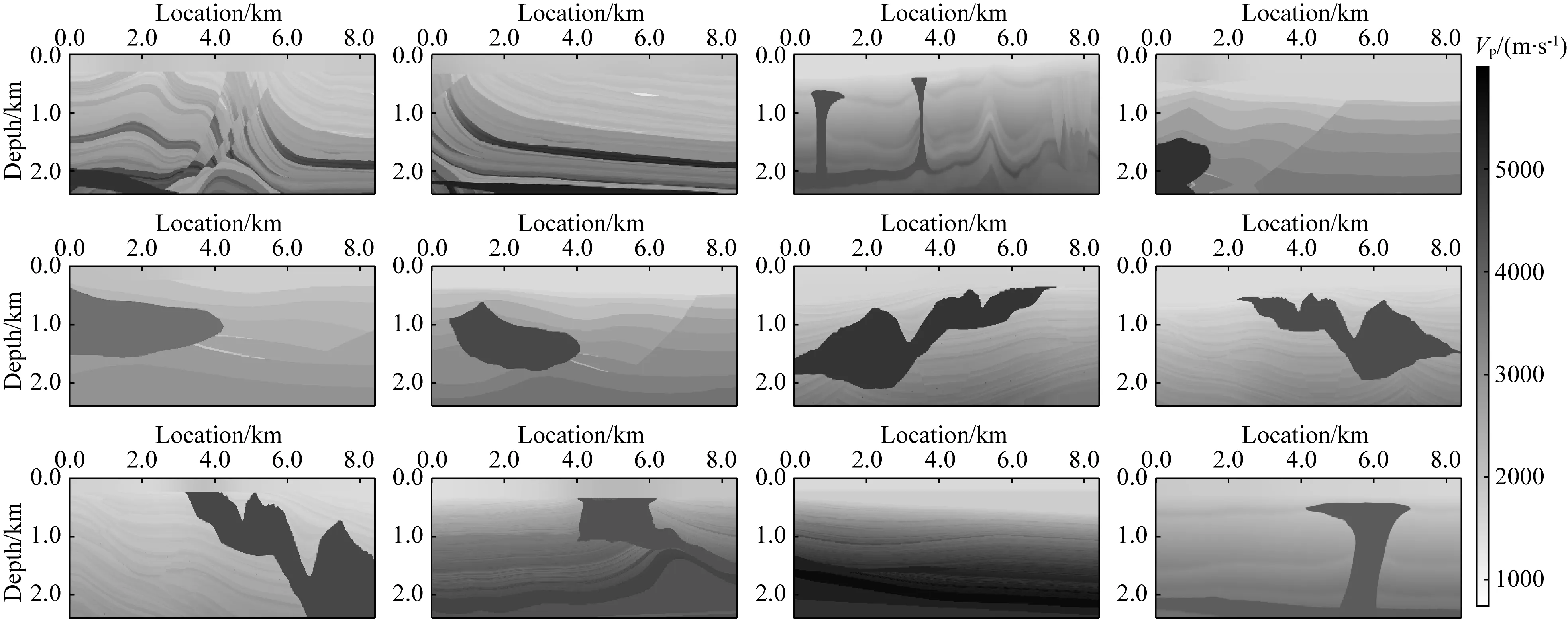
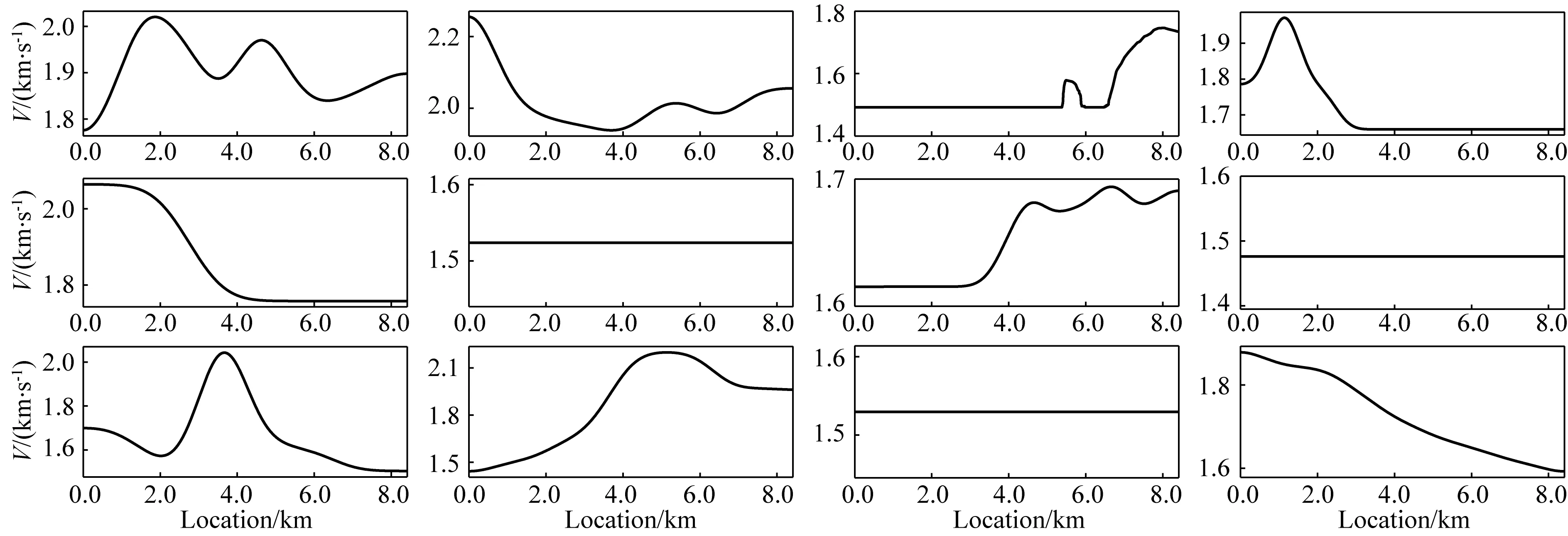
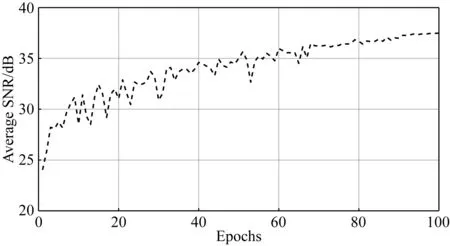
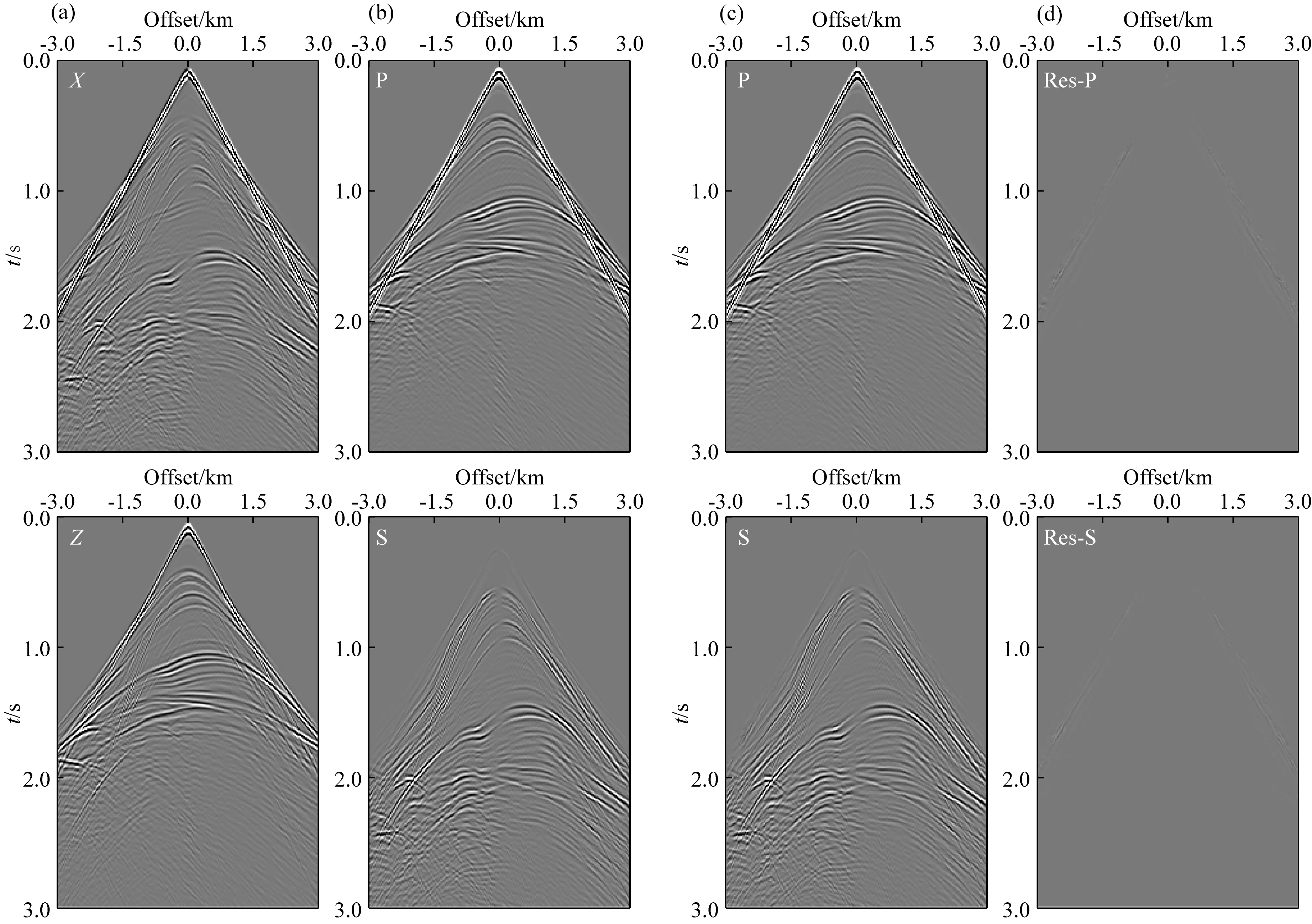
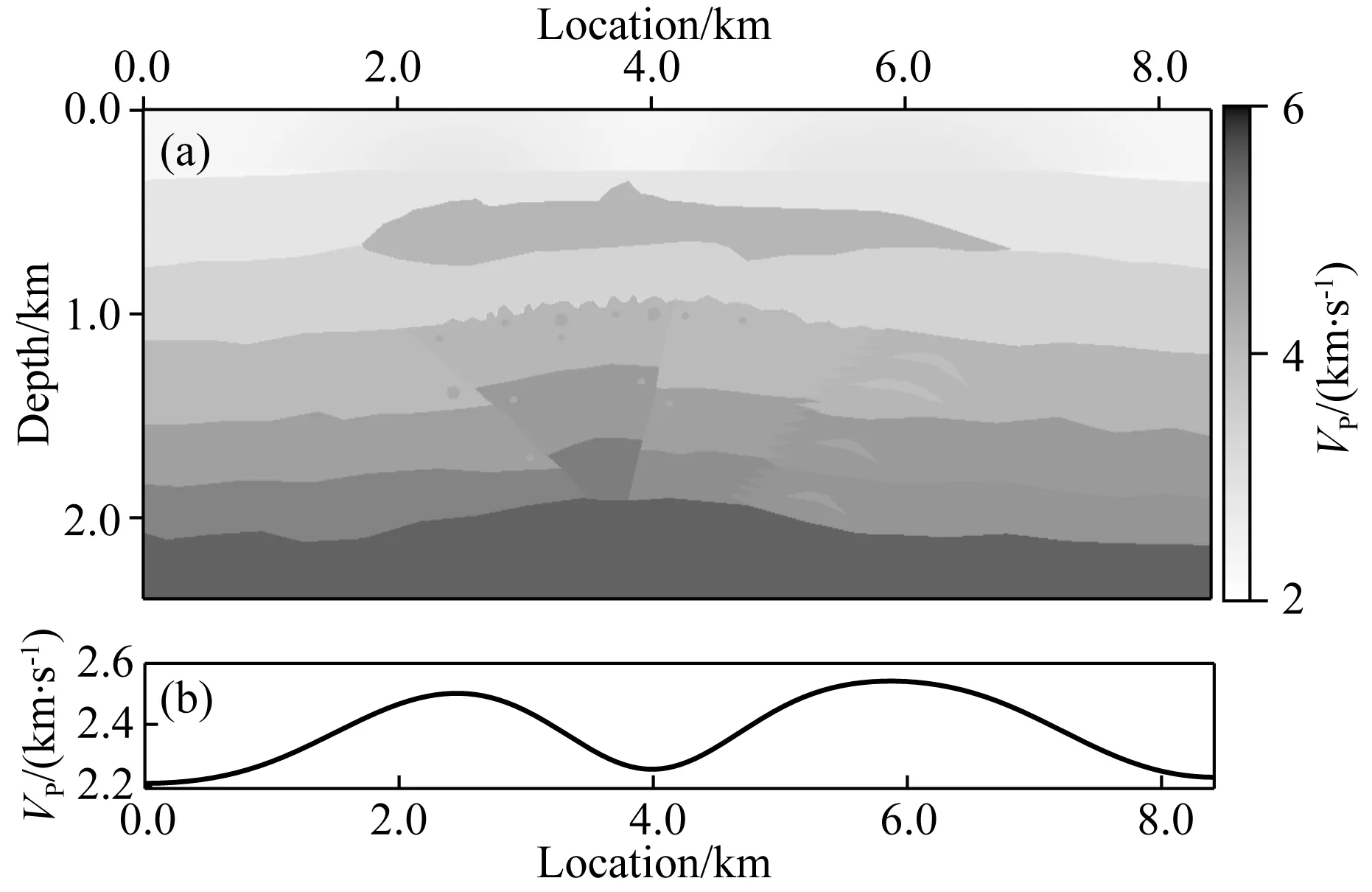
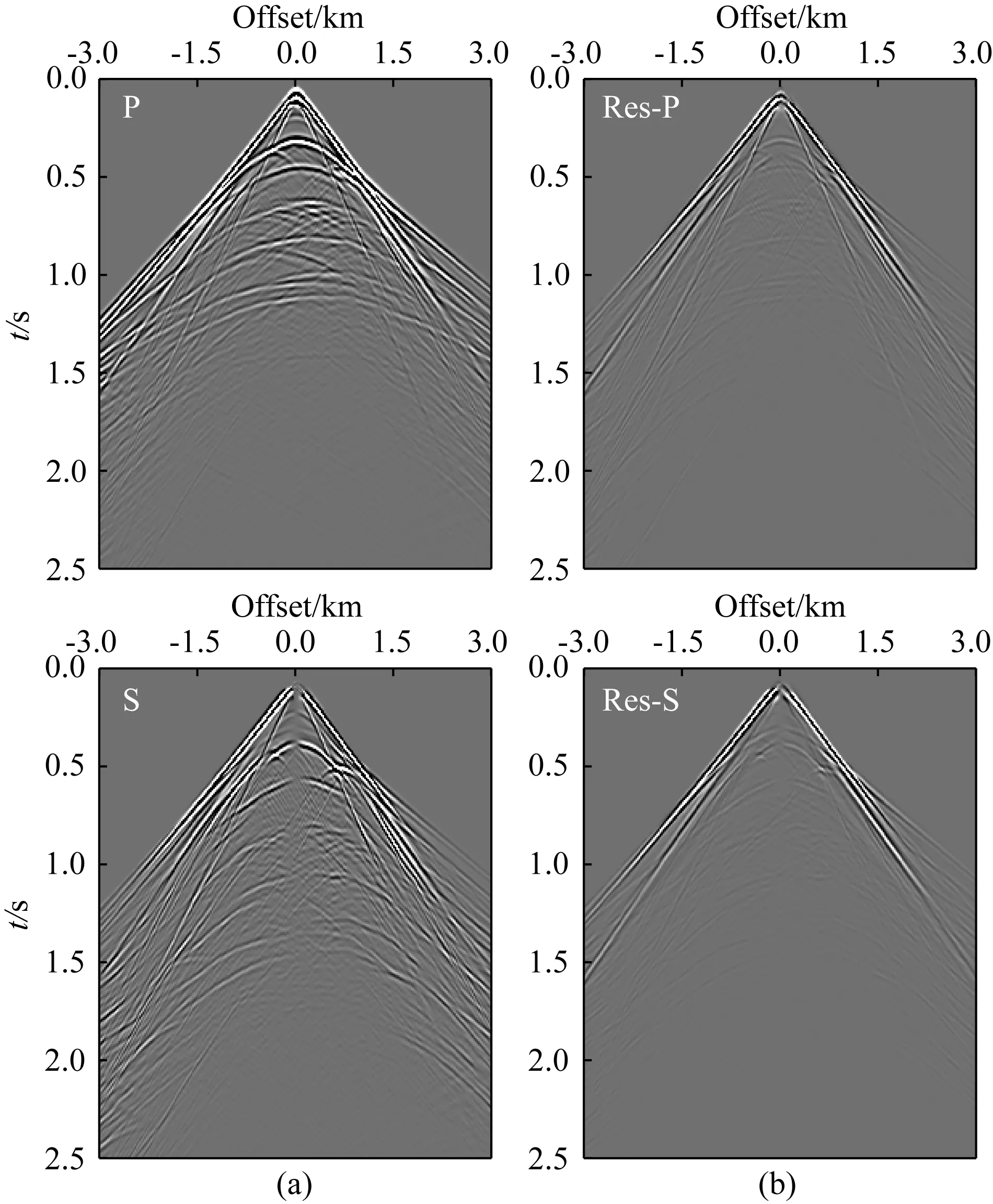
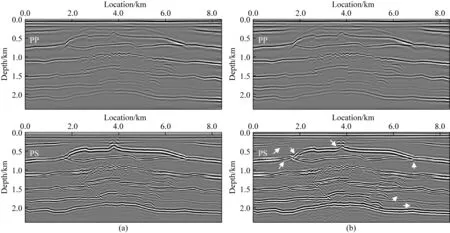
v(x,z)=v(x,h)+αx-β(h-z)γ,z (3) 其中平滑后的v(x,h)与α共同决定表层介质的横向非均匀性变化,而系数β与γ则控制表层介质的垂向非均匀性.这些系数在合理范围内随机取值,以保证表层介质纵波速度符合一般地质规律(如宏观上随深度递增). 按上述步骤构建大量纵波速度模型之后,在合适范围内选定不同的纵横波速度比得到对应的横波速度模型,并由经验公式转换获得密度模型(如Gardner et al.,1974).至此,样本库为人工合成多分量地震记录并生成丰富的标签数据提供了大量地质构造特征与表层介质条件均具有广泛代表性的弹性参数模型. 即便已知表层纵横波速度参数,基于波动理论的多分量记录P/S分离方法在远炮检距或大入射角情况下也容易产生模式泄露.因此,为了提高标签数据的可靠性,本文基于各向同性介质假设,针对模型样本库中任意一组弹性参数模型,先通过交错网格有限差分算法求解弹性波方程,获得时间-空间域的弹性矢量场u(x).然后根据亥姆霍兹分解理论,利用散度、旋度运算从u(x)中分离出P波或S波数据,即: (4) 本节基于前文方法步骤建立模型样本库和P/S分离标签数据集,然后进行U-net神经网络模型的训练、验证和测试.为了评估网络模型的泛化能力和样本构建策略的有效性,我们把训练好的网络用于新的弹性模型,检验对其合成多分量记录P/S分离的应用效果,并与常规基于表层速度模型的偏振投影分离结果进行比较.为了定量分析深度学习方法的性能表现,这里先选用信噪比指标来评价P/S分离结果,即: (5) 其中A为信号的均方根振幅.最终通过分离后P波和S波数据的叠前深度偏移成像质量进一步检验方法的有效性. 首先,对从SEG和EAGE官网下载的标准速度模型进行仿射变换,并从中随机裁剪得到不同长宽比的基础模型.然后对每个基础模型的纵波速度施加20%以内的整体随机扰动,并将模型缩放至相同宽度.接着构建其表层速度结构:先对这些模型的顶界面进行不同尺度的高斯平滑,再根据公式(3),设定α=0,β∈(0,1),γ∈(0.5,2),将平滑后的顶界面速度向上延拓得到最终模型的表层结构,其厚度在240~480 m的范围内.经过上述步骤之后,表层速度的横向与纵向变化既与原有模型相关,又加入了一些随机扰动和不同尺度的空间非均匀性,使得表层速度结构具有更为丰富的变化特征.最终为样本库构建出300个弹性参数模型.如图2所示,即便源自同一标准模型,变换后的最终模型的速度结构也有不同程度的差异,且符合一般的地质规律.它们的表层速度既可能是常数,也可能具有复杂的横向非均匀性(图3).在此基础上,按照纵横波速度比在1.49至2.0内变化以及Gardner经验关系,由纵波速度模型变换得到横波速度与密度模型,完成弹性参数模型样本库的构建. 图2 弹性参数模型样本库中部分纵波速度结构Fig.2 Some P-wave velocity structures of the elastic model library 图3 图2中模型表层纵波速度的横向变化曲线Fig.3 The lateral variations of the surface velocity for the models in Fig.2 接下来针对任意一组弹性参数模型,采用交错网格高阶有限差分算法合成二维二分量(2D2C)地震记录,并在数值模拟过程中利用散度-旋度运算分离出标量P和S波信号,生成共炮域的多分量地震数据及对应的P/S波记录.为了降低标签数据集的制作成本,我们在每组模型上仅以均匀的间隔放置10个P波点震源,每炮合成数据包含1001个接收道,道间距为6 m.震源时间函数采用主频为20 Hz的雷克子波,记录时间总长为3 s,时间采样间隔为1 ms.最终整个标签数据集包含3000组2D2C炮记录及对应的标量P/S波数据.图4显示了其中两组标签数据,包含原始炮记录的X和Z分量以及分离的P和S波共炮道集.由于地质构造和弹性参数结构的明显差异,矢量弹性波记录对应的P和S波反射同相轴有不同的时距关系和振幅变化特征. 图4 部分标签数据集(a)和(b)代表两组弹性模型对应的合成2D2C共炮记录及其标量P/S波道集.Fig.4 Part of the labeled dataset(a) and (b) represent the 2D2C common-shot data and the corresponding scalar P/S gathers, with respect to two different elastic models. 在训练网络之前,先对炮集数据进行归一化处理.将每炮X与Z分量视为整体,合并统计其标准差,再将这两个分量及其解耦的P/S分量标签分别除以该值.注意,这个过程不会影响数据本身的信噪比.随后根据弹性模型样本将整个标签数据集以80%、10%、10%的比例随机划分为训练集、验证集以及测试集,并且保证同一模型对应的炮记录不会同时出现在训练、验证和测试集中.在训练阶段,将数据随机裁剪为256×256的大小,最终获得48000个数据块用作训练样本集. 针对图1中的U-net网络结构,设置第一个基本卷积单元中的卷积核数为32(即N=32).网络训练的批量大小(Batch Size)为32,选用Adam算法(Kingma and Ba,2014)作为优化器更新网络参数.初始学习率设为0.0005,并随训练轮次按指数规律衰减.实验中使用NVIDIA GeForce RTX 3090显卡进行网络模型训练,每次迭代耗时约1.4 s.在每轮训练结束后检验网络模型在验证集上的表现.在验证过程中,通过滑动窗口的方式对完整的炮集数据进行波型分离(预测),滑窗大小为256×256.最后合并统计P和S波炮集数据的平均信噪比对验证过程进行评价.如图5所示,经过100个训练轮次(Epoch),在验证集上的最高平均信噪比达到37.49 dB.最终选取在验证集上表现最佳的网络模型用于后续的测试.在测试集上,网络预测的P波数据平均信噪比为40.49 dB,S波数据的平均信噪比为25.94 dB,其中某炮数据的分离结果如图6所示.可见,网络预测结果(图6c)十分接近精确解耦的P/S数据(图6b),仅在直达波附近有微小偏差(图6d).从近炮检距和远炮检距单道记录振幅曲线也可以发现网络预测的P与S波同标签数据匹配得非常好,尤其是其中的反射信号一致性非常高(图7).由于P波直达波的强烈干扰,网络预测的S波信号在远炮检距处出现了少量的模式泄漏.如后文所展示的,这些微弱的误差几乎不会对多炮偏移叠加成像结果产生明显的影响. 图5 网络模型在验证集上的平均信噪比随训练轮次的变化曲线Fig.5 The average SNR of the network model on the validation set along with training epochs 图6 测试集上的P/S分离结果(a) 输入网络的多分量地震数据; (b) P波与S波数据标签; (c) 网络预测结果; (d) 预测结果与标签数据之间的残差.Fig.6 The separation results on the testing set(a) The input multi-component seismic data; (b) The labeled P- and S-wave data; (c) The predicted results with trained network; (d) The residuals between (b) and (c). 图7 测试集结果单道振幅比较(a) 近炮检距P波与S波信号(offset=-240 m); (b) 远炮检距P波与S波信号(offset=-2760 m).Fig.7 Single-trace comparisons of the testing set(a) P- and S-wave signals at near offset (offset=-240 m); (b) P- and S-wave signal at far offset (offset=-2760 m). 为了证实本文P/S分离深度学习方法的有效性,接下来构建一个全新的弹性模型,并对合成的多分量地震数据进行处理.该模型纵波速度结构如图8所示,其表层含较大幅度的横向与纵向速度变化,浅部存在高速火成岩体,其下方存在溶洞、断层等复杂构造以及一些速度反差较小的岩性界面,这些复杂地质特征与弹性参数结构导致合成的多分量数据波场响应十分复杂,给P/S分离带来一定的挑战.这里采用地表2D2C观测方式,共模拟200炮多分量地震记录.震源时间函数采用主频为20 Hz的雷克子波,接收点横向间隔为6 m, 记录时间总长为2.5 s,时间采样步长为1 ms.图9显示了其中震源位于3000 m处的单炮X和Z分量及其P/S数据标签. 图8 用于泛化能力测试的速度模型(a) 纵波速度; (b) 表层速度横向变化曲线.Fig.8 The velocity model for generalization test(a) P-wave velocity; (b) Lateral velocity variation in the shallow part. 图9 目标测试数据P/S分离结果(a) 原始多分量地震数据; (b) P波与S波标签; (c) 网络预测结果; (d) 网络预测结果与标签数据之间的残差.Fig.9 The P/S separation result of the target test data(a) The original multi-component seismic data; (b) The labeled P- and S-wave data; (c) The predicted results with trained network; (d) The residual between (b) and (c). 首先,将训练与验证后的网络用于该数据体的P/S分离,预测结果如图9c所示,其中P波道集平均信噪比为35.257 dB,S波道集平均信噪比为18.540 dB.可见,将网络直接应用到情况复杂的新数据体上,依然有很高的预测精度.从单道振幅曲线可发现,无论在近炮检距或远炮检距,网络预测的P波与参考数据(即在数值模拟过程中的精确解耦结果)很一致.同样,由于强振幅直达P波的干扰,网络预测的S波会在干扰区存在少量误差.值得注意的是,这个测试过程完全不依赖新模型的表层介质参数.此外,为了说明本文模型样本增广的重要性,特意仅基于SEG/EAGE公开的纵波速度模型按与前文一致的纵横波速度比和Gardner经验关系转换得到横波速度和密度结构,然后利用这些有限的弹性参数模型生成一套“小型的”P/S分离标签数据集.其中在每个模型上合成50炮数据,其它观测参数均与前文一致.接着按照相同的步骤进行网络的训练和验证,最后用这个新的网络模型对图9中的2D2C共炮记录进行处理,发现其P/S分离表现急剧恶化(图10),直达波与反射波存在不同程度的信号串扰.预测的P波道集的平均信噪比仅为6.181 dB,S波道集的平均信噪比为-10.010 dB.这表明,只有用于训练网络的弹性模型样本足够多,构造和表层介质特征足够丰富,才能保证训练好的P/S分离网络在处理不包含在模型样本库中的其他弹性介质地面多分量地震记录时有良好的表现. 图10 基于未做增广的数据集训练的网络对目标数据(图9a)的P/S分离结果(a) 网络预测结果; (b) 预测结果与标签数据(图9b)间的残差.Fig.10 The P/S separation of target dataset (Fig.9a) using the trained network without data augmentation(a) The network′s prediction; (b) The residuals between (a) and Fig.9b. 然后,将本文卷积神经网络与常规偏振投影方法(Li et al.,2016)的分离结果进行比较.后者是一种典型的模型驱动方法,它利用P波和S波在接收点处的偏振方向进行波型分离.因此,它需要根据表层介质的纵波和横波速度,按频率-波数域的频散关系分别估算P波和S波在地表的出射和偏振方向.为了模仿实际地震资料处理过程,这里不采用真实的速度参数,而是根据多分量记录中的直达P波的斜率估计表层纵波速度,约为2350 m·s-1.表层横波速度按纵横波速度比1.73换算得到.这样估算的纵横波速度偏离真实情况不到10%.按这种偏振投影方法分离的结果如图11所示,模式泄露或串扰比较明显,这在分离的S波记录上表现地甚为严重(图12).由于表层速度横向剧烈变化,而基于直达波估计的速度误差导致偏振方向存在较大偏差,影响了P/S分离效果.相反,深度学习分离方法不需要提供表层速度模型,而是在从有广泛代表性的标签数据集中训练获得了表层速度与弹性波传播、偏振之间的内在关系,因此在新模型数据上获得了很好的预测表现. 图11 目标数据偏振投影P/S分离结果(a) 分离的P波与S波数据; (b) 预测结果与标签数据(图9b)间的残差.Fig.11 The P/S separation results of the target dataset with polarization projection(a) The separated results; (b) The residuals between (a) and Fig.9b. 图12 目标数据P/S分离结果单道对比(a) 近炮检距P/S信号(offset=-240 m); (b) 远炮检距P/S信号(offset=-2760 m).Fig.12 The single-trace comparison of P/S separation of the target dataset(a) Near-offset trace (offset=-240 m); (b) Far-offset trace (offset=-2760 m). 最后,将分离后的200炮P与S波数据进行逆时偏移(RTM),从反射PP波和PS波的成像结果对比验证P/S分离的效果.如图13,深度神经网络相比于偏振投影方法,其分离结果成像质量更高,火成岩体、断层等地质结构以及速度反差不大的岩性界面刻画更准确、更清晰,而偏振投影方法分离的S波数据存在明显模式泄漏,导致PS成像剖面出现了一些假象和噪声,火成岩边界成像振幅一致性变差(见图中箭头指示). 图13 不同分离方法所得P/S波数据对应的逆时偏移成像结果(a) 网络预测; (b) 偏振投影方法.Fig.13 RTM results of separated P- and S-wave data using different separation methods(a) The trained network; (b) The polarization projection method. 对于监督类深度学习方法而言,标签数据集的丰富程度是确保网络良好泛化性能的关键之一.本文在构建弹性模型样本库时,通过常用的图像变换与地质信息约束(如宏观上速度从浅到深递增),尽可能考虑了地质构造和表层速度结构的多样性.由此制作的P/S分离标签数据具有一定程度的代表性,训练的网络模型在目标测试数据上取得了很好的应用效果.然而,实际地下介质的情况可能更为复杂,陆地或海洋环境的表层介质更是有所不同,在构建弹性模型库时完整地代表地下介质的复杂情况是非常困难的,也会大幅增加标签数据构建与网络模型训练的难度.因此,更为合理的标签数据构建方法是利用目标探区的先验地质信息,在构建弹性模型库时加入符合探区特点的地质模型,这样既可以降低数据标签构建的工作量,又能大幅提高网络模型的泛化性能.当然,地下介质的各向异性、非弹性衰减等更复杂的波场效应对P/S分离也会有显著的影响.若要在智能网络P/S分离中考虑上述效应,就需要在弹性模型库和标签数据制作中加以考虑,这超出了本文的研究范畴. 在本文数值实验中,由于在构建标签数据集时考虑了地质构造和表层速度结构的多样性,训练后的网络模型可以很好地对复杂含火成岩地质模型的合成数据进行P/S分离.为了进一步考察该网络模型的泛化性能,下面讨论数据频带、炮检距范围、信噪比等实际因素可能带来的影响. 为了调查数据频带对网络预测效果的影响,基于图8含火成岩的弹性模型按与图9中实验同样的观测系统,分别用主频为15 Hz和30 Hz的震源子波重新合成2D2C共炮集数据进行试验.将前文训练好的网络(20 Hz主频数据训练)直接用于这两份数据体上,分离结果如图14、图15所示,其中主频15 Hz数据网络预测P波与S波信号的平均信噪比分别为21.354 dB和8.996 dB.而主频30 Hz数据网络预测P波与S波信号的平均信噪比则分别为24.780 dB和13.508 dB.由于这两份新的测试数据与训练集数据在主频上存在偏差,在直达P波同相轴附近的分离效果受到一定影响(见图14d、图15d).然而这部分信号对PP和PS波成像几乎没有贡献,因此分离结果完全在可接受的范围内.这表明本文基于深度学习的P/S分离方法对数据频带有较强适应性.此外,当工区内震源类型多样或子波主频差异较大时,有必要根据先验信息相应地扩充标签数据库,使网络在训练中学会对这些复杂性的应对能力. 图14 主频15 Hz震源子波合成数据的P/S分离结果(a) 多分量地震记录; (b) P波与S波数据标签; (c) 网络预测结果; (d) 预测结果与标签数据的残差.Fig.14 The P/S separation results of the synthetic data modeling with a Ricker′s wavelet of a 15 Hz peak frequency(a) The multi-component recording; (b) The labeled P- and S-wave data; (c) The predicted results with trained network; (d) The residuals between (b) and (c). 图15 主频30 Hz震源子波合成数据P/S分离结果(a) 多分量地震记录; (b) P波与S波数据标签; (c) 网络预测结果; (d) 预测结果与标签数据的残差.Fig.15 The P/S separation results of the synthetic data modeling with a Ricker′s wavelet of a 30 Hz peak frequency(a) The multi-component recording; (b) The labeled P- and S-wave data; (c) The predicted results with trained network; (d) The residuals between (b) and (c). 即便基于准确的近地表速度,基于波动理论的P/S分离方法通常在大炮检距存在明显的误差.这里探究炮检距范围对本文网络预测效果的影响.针对同样的弹性模型,将采集方式由双边观测改为单边观测,合成多分量地震记录的最大炮检距由3 km增大到6 km.我们发现前文训练好的网络在本数据集上依然有较好表现(图16c),信噪比指标甚至略高于双边观测情况(P波平均信噪比为35.446 dB,S波平均信噪比为19.562 dB).基于深度学习的分离结果与标准答案非常一致(见图16b和16c),表明该方法对炮检距范围不敏感.相反,偏振投影分离结果在大炮检距存在明显的模式泄露(如图16d中箭头指示). 图16 大炮检距观测下P/S分离结果(a) 多分量地震数据; (b) P波与S波数据标签; (c) 网络预测结果; (d) 偏振投影分离结果.Fig.16 The P/S separation results for long-offset acquisition(a) The multi-component recording; (b) The labeled P- and S-wave data; (c) The predicted results with trained network; (d) The results using the polarization projection method. 实际地震数据往往受到噪声的干扰,可能影响网络的预测性能.为了测试本文深度学习P/S分离方法的抗噪性,基于前例中的弹性模型,对震源位于4200 m处合成的多分量数据中分别添加不同水平的随机噪声,使其信噪比分别为10 dB、6 dB和2 dB,然后用训练好的网络对其进行波型分离,结果如图17所示.总体而言,网络在含噪数据上的预测性能有所下降,尤其是S波记录中有较强的直达P波信号泄露(图17中箭头所指).随着噪声增强,深部弱信号逐渐被噪声淹没,而且直达波附近的模式泄露也愈发明显.尽管如此,道集中主要反射波和绕射波信号的P/S分离还是有效的,这表明本文方法具有一定的抗噪能力.此外,实际地震资料可能存在自由表面多次波、层间多次波以及面波等相干噪声,可能会给P/S分离的深度学习方法带来挑战.这就需要在标签制作和网络训练中加以恰当的应对.这是下一步值得探究的课题. 图17 含噪数据P/S分离结果(a) 标签数据; 信噪比分别为(b)10 dB、(c)6 dB和(d)2 dB数据的分离结果.Fig.17 The P/S separation results of noisy data(a) The labeled P- and S-wave data, (b) to (d) represent the separated results with (b) 10 dB, (c) 6 dB and (d) 2 dB noise, respectively. 针对地面多分量地震数据P/S分离问题,本文提出了一种基于U-net网络结构的深度学习方法,强调了标签数据集的合理构建及其意义.以SEG/EAGE公开的大量标准模型为基础,通过仿射变换、随机剪裁、表层扩充等数据增广方式构建了样本丰富、代表性强的弹性参数模型库.基于所有模型样本,通过弹性波数值模拟合成多分量地震记录,并利用亥姆霍兹分解创建高质量的P/S分离标签数据集.将不同分量的地震炮集数据视为U-net网络的多通道输入,按照深度学习机制预测(分离)每个时间-空间样点的P波与S波成分.训练与验证后的深度神经网络在测试集上获得了很好的P/S分离结果,证实了模型样本库和标签数据集的创建方式明显提高网络的泛化能力.网络对数据频带、炮检距范围和信噪比变化也有一定的适应性.相比于经典的偏振投影方法,本文方法克服了对表层速度参数的依赖性和长炮检距模式泄漏问题,提升了PP和PS波叠前深度偏移成像质量.本文P/S分离深度学习方法对相干噪声的适应性和实际多分量地震数据处理是下一步需要开展的工作. 致谢感谢多位审稿人对本文提出的宝贵建议.2.2 多分量记录P/S分离标签数据集

3 数值实验
3.1 训练数据集

3.2 网络训练、验证及测试

3.3 网络模型泛化能力测试



4 讨论
4.1 数据频带


4.2 炮检距范围
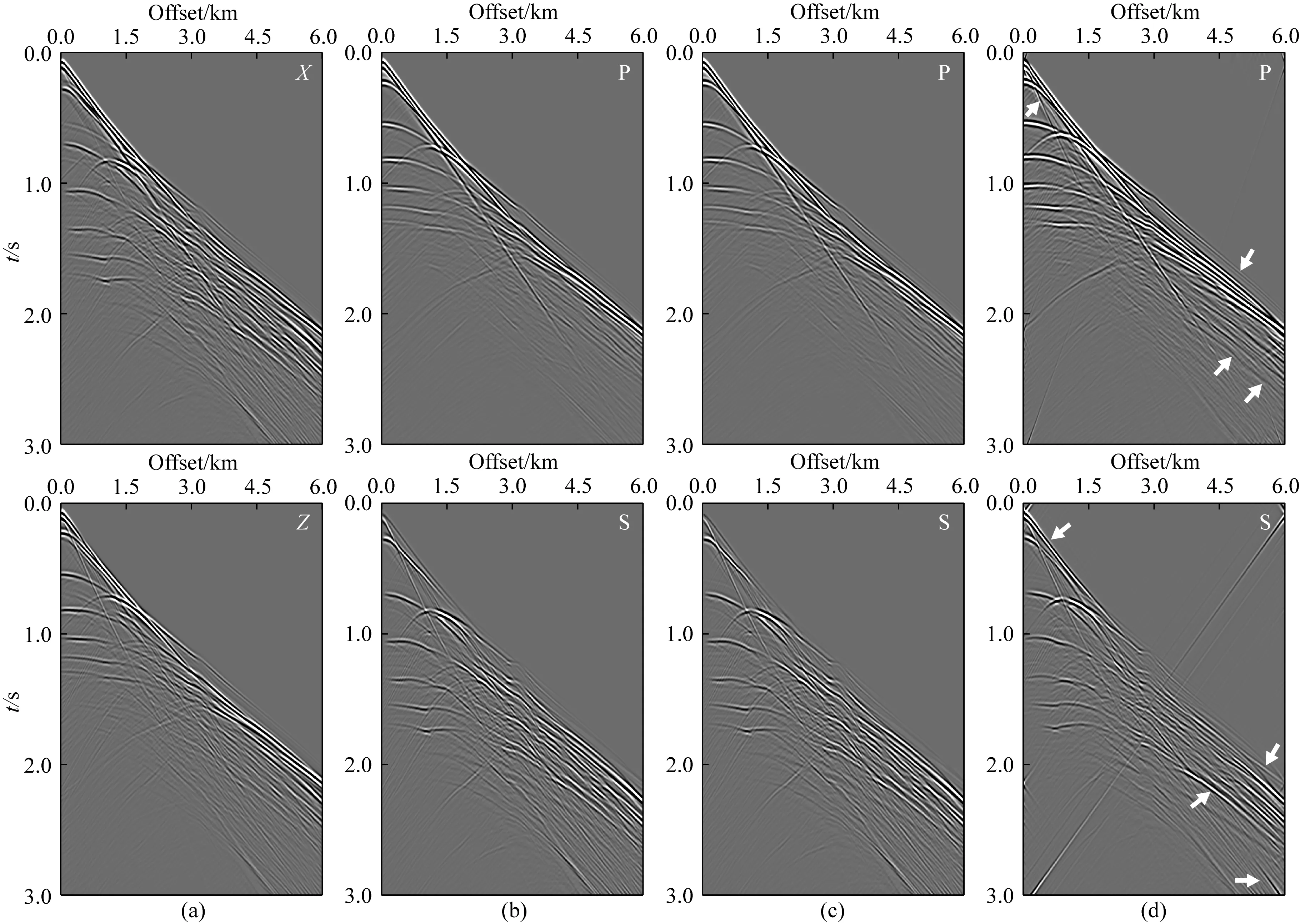
4.3 信噪比

5 结论
