基于Info-gap 理论的巷(隧)道围岩岩爆稳健可靠性预测

张晓君 魏金祝 刘 啸 王宇晨

(1.山东理工大学资源与环境工程学院,山东 淄博 255000;2.山东理工大学矿山工程技术研究所,山东 淄博 255000;3.山东省冶金设计院股份有限公司,山东 济南 250101)

岩爆是深部地下空间开挖与资源开采过程中亟待解决的问题,是前沿研究的热点和难点。岩爆的发生源于其内因和外因的共同作用,很多学者结合内外因,开展了岩爆预测研究。仝跃等[1]基于PSO-SVM算法和岩爆实测数据,对岩爆预测参数的敏感性做出了分析;轩俊杰等[2]基于应力场反演和弹性应变能积聚、汤志立等[3]基于过采样和客观赋权法、谭文侃等[4]基于LOF 与改进SMOTE 算法组合、李明亮等[5]基于变异系数与序关分析法—多维正态云模型、何佳其等[6]通过引入梯度应力强度、吴枋胤等[7]基于萤火虫投影寻踪算法(FA-PP)、田睿等[8]基于RFAHP-云模型、孙臣生[9]基于改进MATLAB-BP 神经网络算法开展了岩爆等级预测工作。当前岩爆预测工作基本上是以确定性参数值代入模型的方法来得出结果,其严格依赖于物理力学等参数的准确性。实际上巷(隧)道围岩的物理力学参数值存在较大的变异性,作为荷载的应力场在不同位置也存在差别,加之室内、现场测试数据有限,对岩爆预测结果的可靠性造成较大影响。

鉴于巷(隧)道围岩的物理、力学及环境等参数的不确定性及现有岩爆预测方法对数据准确性的依赖性较强,需要探寻定量处理参数不确定性问题的新方法。不确定性问题可以用概率论和模糊理论来处理,但概率和模糊预测模型需要较多的数据且相关计算量较大,同时概率可靠性对概率模型参数也很敏感,工程中难以获得大量的测试数据,且数据存在明显变异性,在一定程度上影响了该方法在岩爆预测方面的应用。岩爆常发生在完整或比较完整的岩体中,具有岩爆倾向性的巷(隧)道围岩对损伤有很强的临界敏感性,因此参数值的微小变化都可能引发岩爆。而工程岩体物理、力学、环境等参数的变化范围存在或大或小的波动,这种波动对于具有岩爆倾向性的围岩是不可忽视的。很多情况下,工程岩体物理、力学、环境等参数的变化范围可大体确定,因此,基于区间理论的非概率可靠性的方法来解决参数不确定性问题具备一定优势[10-12]。

综上可见,考虑工程岩体物理、力学、环境等参数波动幅度的岩爆预测方法将更符合实际,预测结果也更可靠。基于Info-gap 理论的稳健性分析方法正好解决上述问题[13-14],目前尚未应用此方法开展岩爆预测研究的报道。本研究基于Info-gap 理论,考虑巷(隧)道围岩物理、力学、环境等参数的波动变化,建立岩爆烈度预测模型,通过工程实例探讨各参数对岩爆预测结果的影响,为岩爆预测及控制提供依据。

1 基于Info-gap 理论的岩爆预测

1.1 Info-gap 模型

影响岩爆预测结果的因素有很多,存在很多不确定性变量,可分为两大类。一类是与防控岩爆措施有关的可控变量,比如岩爆解危参数、岩爆支护参数、岩爆智能调控参数等,这些参数可以根据具体情况进行调整,使其处于正常的防控工作状态,属于设计变量,用向量u表示。另一类是巷(隧)道本身受到的荷载及自身的物理力学参数等变量,这些参数天然具有不确定性,难以根据具体情况进行调整,属于设计参数,这些不可控变量用向量v来表示。综合以上,可得到岩爆预测的巷(隧)道围岩状态功能函数M(u,v),即为含有设计变量u和设计参数v的岩爆预测响应模型。

巷(隧)道围岩系统抵抗不确定性的能力越强,也就越稳定。建立Info-gap 模型来描述巷(隧)道围岩系统不确定因素的波动变化,当模型不确定时:

式中,F为描述某因素的真实函数;为已知近似函数;α为不确定性参数,用以反映不确定因素的波动幅度,即近似函数与真实函数F的偏离程度,其值越大,偏离程度越大,反之越小。

当参量不确定时:

1.2 Info-gap 稳健函数及评价

α作为不确定性参数,也是稳健性的度量指标,这一量值取决于巷(隧) 道围岩状态功能函数M(u,v) 是否满足稳定性要求,针对具有岩爆倾向性的巷(隧)道围岩可得:

表明具有岩爆倾向性的巷(隧)道围岩稳定时的M(u,v) 最小满意值为0。

根据M(u,v) 的取值情况可得到稳健性度量值α的集合:

式中,U(α,) 为描述设计参数v的Info-gap 模型;rl为临界值,对于本文问题,此处取值为0。

具有岩爆倾向性的巷(隧)道围岩的稳健性表达即为式(4)的最小上界:

结合式(4)、式(5),可变为最优规划求解式,即为稳健函数:

根据式(6),α取最大值的情况下,巷(隧)道围岩状态功能函数M(u,v) 大于或等于临界值rl,表明具有岩爆倾向性的巷(隧)道围岩是稳健的、可靠的,不会发生岩爆。(u,rl) 值越大,M(u,v) 可容许不确定参量的扰动或波动变化幅度越大,抵抗应力、物理力学、环境变化的能力越强,反之,稍有扰动或波动,都可能导致其可靠程度降低,诱发失稳岩爆。因此,(u,rl) 可作为稳健可靠度评价指标。具有岩爆倾向性的巷(隧)道围岩稳定的稳健评价模型为

式中,(u,rl) 为稳健评价指标;αc为不确定参量变化幅值的最大值,也是岩爆预测评价的临界值,具体可由式(2)确定。式(7)即为岩爆预测的评价模型(图1),满足式(7)条件时将不发生岩爆,形成由(u,rl) 和αc控制的稳健区,否则将发生岩爆。岩爆预测评价的临界值αc可作为稳健可靠性设计的阈值用于设计中。

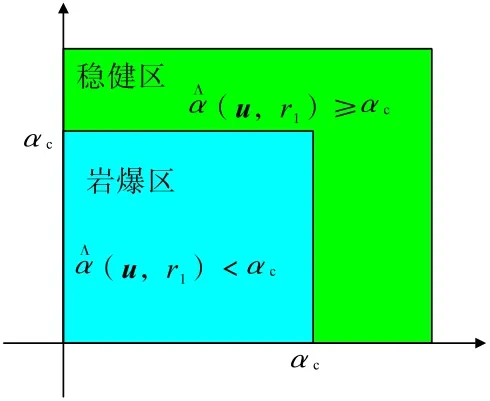
图1 稳健区与岩爆区Fig.1 Robust zone and rockburst zone

根据式(7),定义安全系数F为

由式(7)、式(8)知,当F≥1 时,巷(隧)道围岩是安全的,不会发生岩爆。这里安全系数的含义是不确定参量容许波动范围与不确定参量最大波动范围的比值,该比值越大,巷(隧)道围岩越安全。当F=1时,不确定参量最大波动范围与容许波动范围一致,此时巷(隧)道围岩处于临界安全状态;当F >1 时,不确定参量容许波动范围大于不确定参量最大波动范围,此时巷(隧)道围岩处于安全状态,其值越大,容许波动范围超出最大波动范围更多,安全冗余度越大;当F <1 时,不确定参量容许波动范围小于不确定参量最大波动范围,此时巷(隧)道围岩处于不安全状态,其值越小越不安全。这里定义的安全系数F考虑了参量波动变化,具有明确的含义,可以较好地评价巷(隧)道围岩安全性。

对于工程设计而言,根据给定的安全系数Fl,可得到满足要求的设计参量容许波动范围:

2 岩爆预测的功能函数及流程

2.1 功能函数

采用抗力—荷载模型,则岩爆预测的功能函数为

式中,R为抗力;S为荷载。

根据弹性理论,可得到圆形巷(隧)道围岩的切向应力即荷载S表达式:

式中,P为竖向地压;λ为侧压系数,可通过现场地应力测试获得;r为离巷(隧)道中心的距离;a为圆形巷(隧)道半径;P0为支护力,可通过实际的支护结构获得;θ为极角。

当r=a,θ=0,P0= 0 时,式(11)变为

对于其他形状的巷(隧)道围岩切向应力,可通过将式(11)中的r替换为r0的当量半径折算法获得:

式中,r0为巷(隧)道的当量半径;s为实际巷(隧)道断面积;k为修正系数,形状为直墙拱形时取1.10。

基于岩石单轴抗压强度,考虑岩爆烈度分级,得到抗力R表达式:

式中,χ为岩爆烈度系数,岩爆烈度分级标准见表1,判定弱岩爆时取0.3,判定中等岩爆时取0.5,判定强岩爆时取0.7;σc为岩石单轴抗压强度。

表1 岩爆烈度分级标准Table 1 Classification standard of rockburst intensities

所以,岩爆预测的功能函数可进一步表示为

考虑最危险的情况,当r=a,θ=0,P0=0 时,式(15)变为

2.2 岩爆烈度预测流程

根据上述分析及给定的岩爆预测资料,具体的岩爆烈度预测流程如下:

(1)根据给定的资料并结合功能函数(式(15))确定各参量的数值、变化范围及名义值,确定用于稳健可靠度评价的不确定参量,得到不确定参量的变化幅值最大值。

(2)考虑危险的情况,首先确定强烈岩爆的发生情况,根据岩爆预测的功能函数(式(15)),岩爆烈度系数χ取0.7,通过最优规划求解式即稳健函数(式(6)),得到稳健可靠度指标(u,rl),再根据稳健评价模型(式(7)),判定其是否发生强烈岩爆。

(3)如果经过评价将发生强烈岩爆,则中等岩爆和弱岩爆必发生,如果经过评价不发生强烈岩爆,则继续评价中等岩爆(χ取0.5),步骤同上。

(4)如果经过评价将发生中等岩爆,则弱岩爆必发生,如果经过评价不发生中等岩爆,则继续评价弱岩爆(χ取0.3);如果经过评价弱岩爆发生,则评定发生弱岩爆,反之不发生岩爆。

3 工程实例与参量分析

采用文献[15]、[16]的资料进行实例分析,根据式(16),考虑最危险的情况,λ、P为不确定参量,侧压系数λ的变化范围为(0.3,0.5),αc(λ)=0.25,竖向地压P的变化范围为(20,40),αc(P)=0.33,则岩爆预测评价的临界值αc= 0.33。岩石单轴抗压强度σc取最大值130 MPa,考虑强烈岩爆的发生情况,岩爆烈度系数χ取0.7,如果经过评价确定发生强烈岩爆,上述计算只是考虑最危险的位置(临空面),则中等岩爆和弱岩爆必发生,无须再进行评价。

稳健可靠度评价指标(u,rl) 求解,由式(6)知:

通过优化求解求得(u,rl)=0.2,(u,rl) 与αc进行比较,可见(u,rl)<αc,表明不确定参量波动范围在容许波动范围外(图2)。由式(8)计算得安全系数F为0.6(<1),系统是不稳健、不安全的,将会发生强烈岩爆;同理,中等岩爆、弱岩爆也必然发生。工程的实际情况是轻微岩爆28 段,中等岩爆11段,强烈岩爆4 段,分析结果与其基本一致,表明基于Info-gap 理论的岩爆预测模型是合理和适用的。

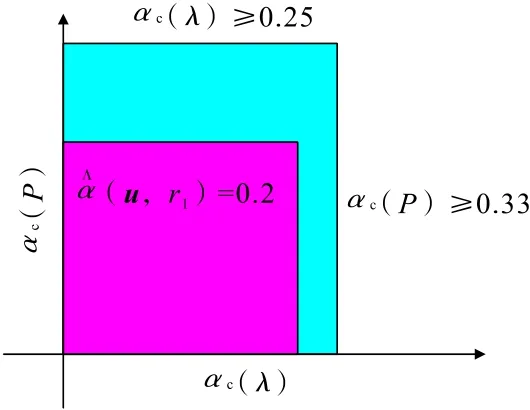
图2 稳健可靠度指标与参量变化幅度Fig.2 Robust reliability index and amplitude of parameter change

如果考虑支护力的控制作用,在其他参量相同的情况下,可得到稳健可靠度评价指标(u,rl) 随支护力P0的变化关系,见图3。可见,随支护力的增加,稳健可靠度指标增加,当支护力达到7.5 MPa 时,(u,rl)=αc= 0.33,此时安全系数为1,将不发生强烈岩爆,表明支护对岩爆烈度降低及岩爆发生与否有重要控制性作用,可通过稳健可靠性设计指导岩爆支护设计。

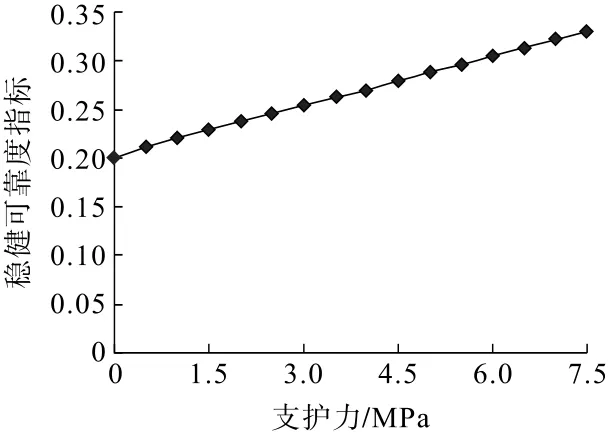
图3 稳健可靠度指标随支护力的变化Fig.3 Variation of robust reliability index with supporting force

当θ=0,P0= 0 时,在其他参量相同的情况下,可得到稳健可靠度评价指标(u,rl) 随r/a的变化关系,见图4。可见,随r/a的增加,稳健可靠度指标增加明显,当r/a=1.05 时,(u,rl)=0.336,不再发生强烈岩爆。当巷(隧)道半径为4 m 时,强烈岩爆发生深度为0.2 m,超过该深度强烈岩爆不再发生,但依然会发生中等及弱岩爆,同样可计算出相应的临界深度。由此可见,强岩爆的发生必伴随着中等乃至弱岩爆的发生,爆坑深度也最深,所以爆坑呈现V形;中等岩爆的发生伴随着弱岩爆,爆坑深度次之,所以爆坑呈现弧形;仅发生弱岩爆时爆坑深度最小。对于巷(隧)道围岩内部而言,所处位置不同,其岩爆烈度是不同的,通过稳健可靠性分析可得出不同岩爆烈度的岩爆深度。

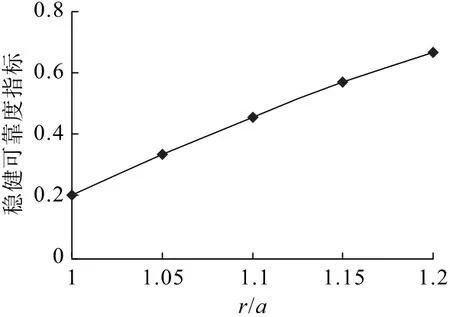
图4 稳健可靠度指标随r/a 的变化Fig.4 Variation of robust reliability index with r/a

当r=a,θ=0,P0=0 时,在其他参量同上的情况下,得到稳健可靠度评价指标(u,rl) 随侧压系数λ名义值、竖向地压P名义值的变化关系见图5。可见,随侧压系数λ名义值的增加,稳健可靠度指标增加明显,随竖向地压P名义值的增加其增加程度明显降低;随垂直地压P名义值的增加,稳健可靠度指标明显降低,发生强岩爆的可能性不断增加。表明地应力值的变化对岩爆烈度及岩爆发生与否有重要影响。

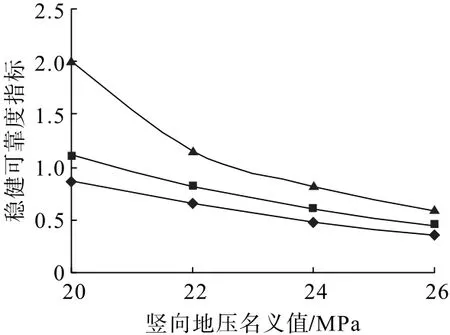
图5 稳健可靠度指标随垂直地压名义值的变化Fig.5 Variation of robust reliability index with nominal value of vertical ground pressure

需要特别说明的是,由于岩爆本身的复杂性及对功能函数的简化等原因,考虑的岩爆因素非常有限,更深入的岩爆预测模型还有待进一步研究。

4 结论

(1)考虑巷(隧)道围岩物理、力学、环境等参数的变化幅度,针对岩爆预测,建立了基于Info-gap 理论的Info-gap 模型、稳健函数及评价模型,得出的稳健评价模型即为岩爆预测的评价模型,满足模型条件将不发生岩爆,形成由(u,rl) 和αc控制的稳健区,否则将发生岩爆。定义了具有明确含义的安全系数F,考虑了参量波动变化,可以较好地评价巷(隧)道围岩安全性。

(2)基于岩爆烈度分级标准,采用抗力—荷载模型,建立了岩爆预测的功能函数。结合岩爆预测评价模型,若经过评价将发生强烈岩爆,则中等岩爆和弱岩爆必发生;若经过评价其不发生强烈岩爆,则继续评价中等岩爆,若经过评价将发生中等岩爆,则弱岩爆必发生;若经过评价其不发生中等岩爆,则继续评价弱岩爆,若经过评价其发生弱岩爆,则评定为弱岩爆,反之不发生岩爆。

(3)通过工程实例验证了基于Info-gap 理论的岩爆预测模型可靠性,并探讨了各参数对岩爆预测结果的影响。随支护力的增加,稳健可靠度指标增加,支护对岩爆烈度降低及岩爆发生与否有重要控制性作用,可通过稳健可靠性设计指导岩爆支护设计。随着离巷(隧)道围岩临空面距离的增加,稳健可靠度指标增加明显。对于巷(隧)道围岩内部而言,所处位置不同,其岩爆烈度是不同的,通过稳健可靠性分析可得出不同岩爆烈度的岩爆深度。地应力值的变化对岩爆烈度及岩爆发生与否有重要影响。