基于DAEKF 算法的锂离子电池主要状态在线联合估计

罗玉涛 吴志强

（华南理工大学 机械与汽车工程学院， 广东 广州 510640）

三元锂离子电池因其单体电压高、能量密度大、适用温度范围广等优点，已成为电动汽车动力电池的首选。但由于电池内部电化学反应动力学机理和电、热、力等多物理场耦合的复杂性，使得如何准确、稳定地在线估计三元锂离子电池的主要状态，成为了实现先进电池管理、保障电动汽车安全与节能时亟待解决的问题。

锂离子电池的主要状态包括荷电状态（State of Charge， SOC）、能量状态（State of Energy， SOE）和健康状态（State of Heath， SOH）。SOC针对电池的剩余电量，指示着系统的可运行时间和充放电策略制定，是电池状态中最核心的内容之一；SOE是表征电动汽车的续航参数指标；SOH是用于评价锂离子电池剩余寿命及剩余价值的量化指标。除了传统的安时积分法［1］，锂离子电池SOC和SOH的估计方法大致可分为基于数据驱动的方法［2-3］、基于模型的方法［4-5］和SOC+SOH 联合估计法［6-7］，在这些方法中，扩展卡尔曼滤波（Extended Kalman Filter， EKF）［8-9］得到了广泛的应用。在锂离子电池的3 种主要状态中，SOC 只能代表剩余容量，不能代表可用能量储备［10］，SOE 才能更有效地反映电池当前时刻及历史充放电工况的影响，对续驶里程和续航时间的估计更为可靠［11］。然而，SOE 作为反映续航能力的主要状态却往往被忽略。SOE 的估计方法中，功率积分法［12］这种开环方法不可避免地会由于不确定噪声、传感器采样率和测量缺陷而产生累积误差，滤波类算法仍是SOE 估计的主要方法［13-15］。Li 等［16］通过CKF（Cubature Kalman Filter，容积卡尔曼滤波）算法与递推最小二乘在线参数辨识算法对锂离子电池的能量状态进行了估算，得最大估算误差为4.2%。

文中针对三元锂离子电池SOC、SOE和SOH这3 种主要状态的在线联合估计问题，提出一种基于双自适应扩展卡尔曼滤波（Double Adaptive Ex⁃tended Kalman Filter，DAEKF）算法的多时间尺度主要状态在线联合估计方法。在二阶RC 模型基础上构建DAEKF 算法的状态空间方程，采用带遗忘因子的递推最小二乘法（Forgetting Factor Recursive Least Squares，FFRLS）进行在线参数辨识，通过自适应协方差变化来克服不确定噪声干扰、传感器采样率限制和测量缺陷的影响，以较长的时间尺度估计SOH，以较短的时间尺度估计SOC和SOE，实现对锂离子电池3 种主要状态的在线联合估计。最后，通过NVR18650B 型锂离子电池的充放电实验来进行方法精度、有效性及稳定性的验证，以期提高对锂离子电池SOC、SOE和SOH的估计精度及稳定性，实现三元锂离子电池3种主要状态的在线联合估计。

1 电池模型的建立

1.1 二阶RC模型

二阶RC模型由两个RC网络串联，能够同时考虑欧姆内阻、电化学极化和浓差极化，如图1 所示。图1 中，Ut为电池端电压，UOC为开路电压（Open Circuit Voltage，OCV），iL为电池电流，R0为欧姆内阻，R1和C1分别为浓差极化电阻和电容，R2和C2分别为电化学极化电阻和电容，U1和U2分别为两个RC网络两端的电压［17］。

图1 二阶RC等效电路模型示意图Fig.1 Schematic diagram of second-order RC equivalent cir⁃cuit model

规定放电电流为正，充电电流为负，由基尔霍夫电压定律可得二阶RC 模型中的动态特性微分方程如下：

二阶RC模型中的端电压输出方程为

1.2 OCV曲线拟合

通过放电静置法进行锂离子电池的OCV 测试，将静置过程中趋于稳定的电池端电压视为锂离子电池的OCV［18］。在不同荷电状态下进行测试，再利用Matlab 软件中的Curve Fitting Tool 工具箱对OCV-SOC 曲线进行多项式拟合，获得的八次多项式拟合曲线如图2 所示，其多项式函数关系为：y= -54.515x8＋204.660x7-294.760x6＋197.630x5-56.176x4＋2.889x3＋0.283x2＋0.732x＋3.440（y代表OCV，x代表SOC），r2= 0.999 9，有着较好的拟合精度。

图2 SOC-OCV拟合曲线Fig.2 SOC-OCV fitting curve

1.3 参数辨识

二阶RC 模型中共有5 个待辨识参数，分别是R0、R1、R2、C1和C2。FFRLS 在最小二乘法的基础上引入遗忘因子λ（一般取值0.95~1.00，文中取为0.98），以降低累积数据饱和度［19］，提高在线辨识效率。在此基础上，文中基于锂离子电池1C 放电数据，采用FFRLS来进行在线参数辨识，辨识结果如图3所示，图中t为采样时间。

图3 FFRLS在线参数辨识结果Fig.3 Results of FFRLS online parameter identification

由辨识结果可以看出：在辨识前期，模型参数变化较为剧烈，这是由模型参数初始值的设定与真实值有较大偏差造成的；辨识中后期，各参数的辨识值趋于平缓，并最终收敛于某一数值，此数值视为RC 参数辨识结果。模型的RC 参数均在120 s 内稳定在某一固定值，达到收敛状态，这种快速收敛性能够满足在线实时辨识及状态估计的需求。另外，R1C1和R2C2的乘积呈现为不同的数量级，根据时间常数小、响应速度快的特点［20］，R1C1描述为电池的浓差极化特性，R2C2描述为电池的电化学极化特性，因此辨识结果是符合锂离子电池实际放电特性的。

1.4 参数辨识结果验证

为了验证前述二阶RC模型中OCV-SOC曲线和在线参数辨识结果的有效性，对所建立的模型进行端电压估计，将模型端电压估计值与测量端电压参考值进行对比，结果如图4和5所示。

图4 模型端电压估计值与测量端电压参考值的对比Fig.4 Comparison of the estimated value of the model terminal voltage with the reference value of the measured termi⁃nal voltage

图5 模型端电压估计值与测量端电压参考值的误差Fig.5 Error between the estimated value of the model terminal voltage and the reference value of the measured termi⁃nal voltage

可以看出：由八次多项式拟合及FFRLS在线参数辨识后建立的锂离子电池二阶RC等效电路模型，其端电压估计值与电池测量端电压参考值较为接近，误差基本维持在0.02 V 以内；在放电末期及充电初期，由于电化学反应的不稳定以及电流的剧烈变化而导致误差增大，最大误差为0.018 V。以上结果说明，该参数辨识方法的精度较高，所建立的二阶RC 模型能够应用于锂离子电池的主要状态估计。

2 基于DAEKF 算法的主要状态在线联合估计

2.1 AEKF算法的原理

动力电池在实际应用过程中受到环境噪声、传感器采样率限制及测量缺陷等因素的干扰，广泛应用的EKF算法在计算过程中假设噪声不变，这显然与电池应用工况的复杂性和多变性不相符［21］。噪声信息协方差匹配可以使得EKF中的噪声统计特性随着估计结果的变化而自适应更新，因此，文中提出一种基于DAEKF 算法的三元锂离子电池主要状态在线联合估计方法，以解决各种噪声干扰的影响，同时保证该方法对3种主要状态的估计精度。

对于某一非线性离散系统，可由状态方程和观测方程分别表示为

式中：xk为系统状态；uk为系统输入；yk为系统观测值；ωk表示系统白噪声，其均值为零，协方差为Qk；vk表示均值为零的测量白噪声序列，其协方差为Rk；ω和v相互独立；A、B、C、D分别为对应的线性化后的系数矩阵。AEKF 的计算流程主要分为以下几步。

1）初始化。设置状态观测器的初始值。

2）先验状态预估。将状态和协方差估计从前一时刻k- 1推算到当前时刻k，系统状态预估如下：

误差协方差预估如下：

式中，xk-1和Pk-1分别为k- 1 时刻的系统状态和协方差，和分别为先验估计的状态和协方差。

3）后验估计修正。先计算信息误差ek和卡尔曼增益矩阵Kk，再用k时刻的观测值yk校正状态估计xk和协方差估计Pk，即

同时进行噪声协方差自适应匹配计算，即

式中：Hk为估计协方差函数，用于进行噪声的自适应修正，与EKF 算法假设噪声统计特性不变相比，估计协方差函数Hk将随着测量值和估计值之间的信息误差不断更新，从而对环境噪声、传感器采样率限制及测量缺陷等因素带来的干扰进行自适应匹配，提高估计精度；M为开窗大小。

4）最后输出修正后k时刻的状态和协方差矩阵，同时准备k+ 1时刻的状态估计。

2.2 多时间尺度主要状态在线联合估计

基于DAEKF 算法的多时间尺度主要状态联合估计，其中一个AEKF 算法会建立较长时间周期的宏观时间尺度，另一个则会建立较短时间周期的微观时间尺度，宏观时间尺度的AEKF 用于估计变化较慢的电池参数，微观时间尺度的AEKF 用于估计变化较快的电池状态，以此来实现锂离子电池在多时间尺度下的主要状态联合估计。

基于SOC和SOE的定义［5，10］：

其中SOC(t)和SOE(t)分别为t时刻的荷电状态和能量状态；SOC(0)和SOE(0)分别为初始时刻的荷电状态和能量状态；η为库伦效率，ηe为能量充放电效率，文中均取值为1；Δt为采样间隔；Cact为实际最大可用容量；Ee为额定能量。设系统的状态变量为=[SOCSOEU1U2]，输入为负载电流iL（放电为正，充电为负），输出为电池端电压Ut，将式（1）、（14）和（15）离散化后，可得电池系统的离散状态方程如下：

则电池系统的离散端电压输出方程为

对于SOH 估计模型，将最大可用容量定义为SOH的指标［5］，即

式中，SOH为电池健康状态，Ce为额定最大可用容量。由式（14）得到实际最大可用容量Cact如下：

基于DAEKF 算法的锂离子电池多尺度主要状态在线联合估计的计算流程如图6所示。由式（19）即可得到Cact，经由SOH 的定义即可估计SOH 的状态值，Cact短期内不会发生大的变化，但随着使用时间的增加，Cact将发生衰减。因此考虑将Cact作为宏观尺度下的待估计参数θ，SOC 及SOE 作为微观尺度下的待估计状态χ，以LZ作为时间尺度转换标准，当微观时间尺度累积达到转换标准LZ时，同时进行微观和宏观时间尺度的更新，即同时更新SOC、SOE和Cact。否则只进行微观时间尺度的状态更新，即只更新SOC 和SOE，保持Cact的当前值。LZ的设置将直接影响SOH估计值的跳转，因此，LZ的设置与SOH的估计时间有关，可以根据不同的工况进行选择。为保证估计结果的有效性，文中选择LZ在总工况时长的2/3节点处。

图6 基于DAEKF算法的多尺度主要状态在线联合估计流程图Fig.6 Flow chart of multi-scale multi-state online joint estimation based on DAEKF algorithm

DAEKF 的参数初始化将影响系统的收敛速度，由于没有先验数据，对于初始状态

将其设置为［1 1 0 0］T，初始参数Cact设置为标称容量，同时假设SOC、SOE和SOH的初始误差为10%，U1和U2的初始误差为1 V；过程噪声则受到电池系统动态特性的影响，文中使用的电池标称容量为3.35 A·h，标况下平均一次充电或放电的时间约为4 h，SOC 与SOE 的最大值为100%，最大电压为4.2 V，则ωSOC=(m ax(|dSOC|))2= 100% ×Δt( 3 600 × 4 )，同理可得U1和U2的系统过程噪声为ωUi=(m ax( |dUi|))2= 4.2 × Δt(3 600 × 4)； 假设数据采集设备的误差在1%以内，则测量初始误差为νU=(max(dU))2≈0.001。DAEKF 算法参数初始值的调整与电池系统的标称容量、充放电时间和采样间隔Δt有关［22］。

3 实验验证与分析

3.1 实验设置

为了验证文中提出的基于DAEKF 算法的多尺度主要状态在线联合估计方法的有效性及鲁棒性，选择松下NVR18650B型锂离子电池作为实验对象，电池基本参数信息如表1 所示。采用Neware CT-4000 5V6A 型高性能电池检测系统作为电池监测设备，在实验室环境下对模型进行实验验证，电池检测系统实验平台如图7所示。

表1 实验验证用锂离子电池的基本参数信息Table1 Basic parameter information of lithium-ion battery for test validation

3.2 实验验证工况

进行锂离子电池充放电实验，在上位机中编辑需要进行的实验验证工况的步骤，以验证文中所提方法的准确性及收敛性。

验证工况1 以100%的初始SOC 开始，先进行1 C恒流放电，截止电压为2.75 V；搁置5 min后进行1 C 恒流恒压充电，截止电流为0.05 C，即0.168 A；采样间隔为1 s，总充放电时长为9 760 s，电池平均温度为32.24 ℃。验证工况1 的电压及电流曲线如图8所示。

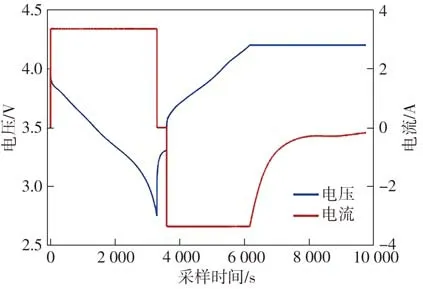
图8 实验验证工况1下的电压、电流曲线Fig.8 Voltage and current curves under experimental verifica⁃tion working condition 1

而为了验证文中方法在动态脉冲工况下在线联合估计的有效性及稳定性，工况2 选择HPPC（Hy⁃brid Pulse Power Characteristic，混合功率脉冲特性）脉冲测试过程，具体步骤如下：

①以1 C的电流大小恒流放电10 s；

②静置40 s；

③以1 C的电流大小恒流充电10 s；

④静置40 s；

⑤以0.33 C 的电流大小恒流放电10% 的SOC值；

⑥静置1 h。

如图9所示，重复步骤①至⑥，直至SOC 达到10%，采样间隔为1 s，总放电时长为42 456 s，电池平均温度为26.52 ℃。

图9 实验验证工况2下的电压、电流曲线Fig.9 Voltage and current curves under experimental verifica⁃tion working condition 2

3.3 结果对比与分析

基于NVR18650B 型电池的充放电实验对文中提出的多时间尺度主要状态在线联合估计方法进行验证，其中SOC、SOE和SOH参考值由电池状态检测系统获得。

如图10所示，在1 C恒流放电及恒流恒压充电的验证工况1下，文中提出的算法能够有效地估计锂离子电池的主要状态SOC和SOE，其中SOC的最大估计误差为0.859%，SOE 的最大估计误差为0.751%，均未超过1.0%。针对SOH，设置状态转换标准LZ= 2 h，在宏观时间尺度下得到Cact=3.116 A·h，以初始额定容量3.35 A·h作为标准值，得实验验证条件下SOH 估计值为93.02%。通过在 上位机设置额定容量，以电池检测系统的最大容量作为参考值，SOH参考值为94.54%，两者绝对误差为1.52%，具体的SOH 估计结果如表2所示。以上结果表明，针对1 C恒流充放电过程，文中提出的方法具有较高的估计精度，同时具有较好的估计收敛性，能够准确估计锂离子电池的SOC、SOE和SOH。

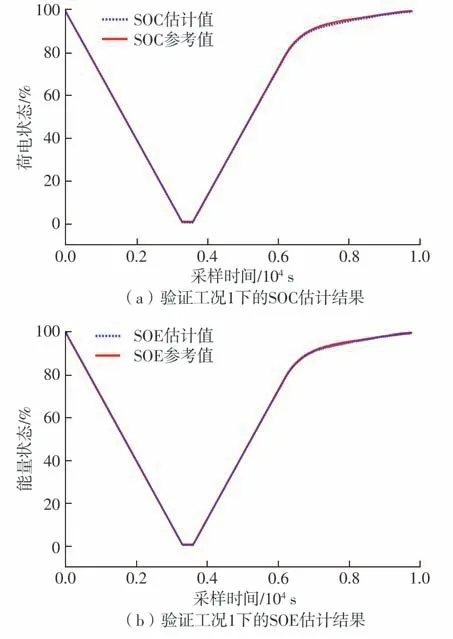
图10 验证工况1下SOC和SOE的估计结果及误差Fig.10 Estimation results and errors of SOC and SOE under verification working condition 1

为了验证文中所提方法的在线估计稳定性，以脉冲测试工况作为验证工况2，其SOC 和SOE 的估计结果及误差如图11 所示。由图可知，针对脉冲工况进行锂离子电池主要状态的在线联合估计时，文中方法同样能够保持较高的估计精度，SOC的最大估计误差为0.848%，SOE 的最大估计误差为0.844%，都保持在1.0%以内。对于SOH，如表2所示，设置状态转换标准LZ= 8 h，在宏观时间尺度下得到Cact=3.149 A·h，以初始额定容量3.35 A·h作为标准值，得到实验验证条件下SOH 估计值为94.00%，参考值为94.54%，两者的绝对误差为0.54%。这说明，文中方法能够有效地针对脉冲工况进行锂离子电池主要状态的在线联合估计，且具有较高的估计精度及收敛稳定性。

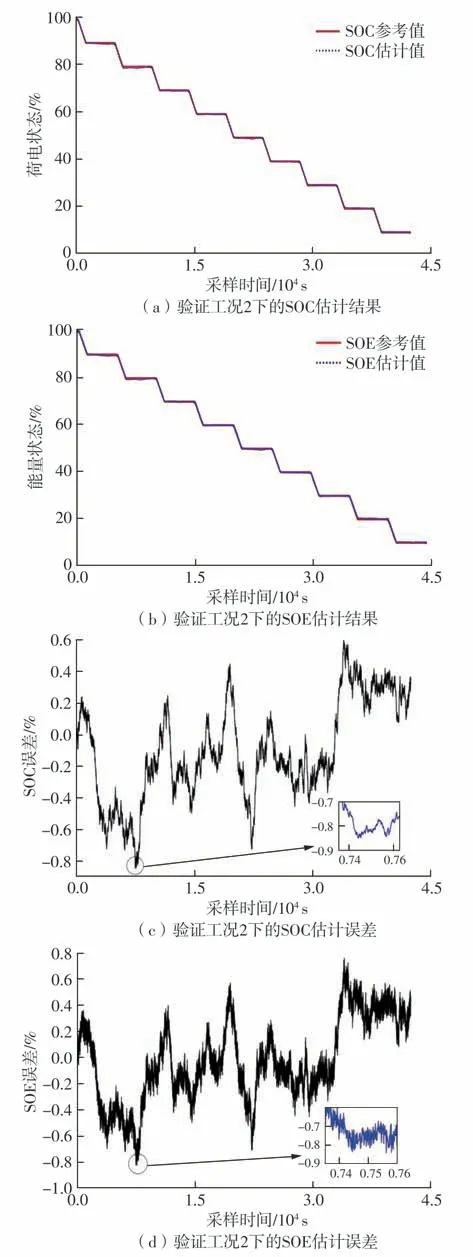
图11 验证工况2下SOC和SOE的估计结果及误差Fig.11 Estimation results and errors of SOC and SOE under verification working condition 2

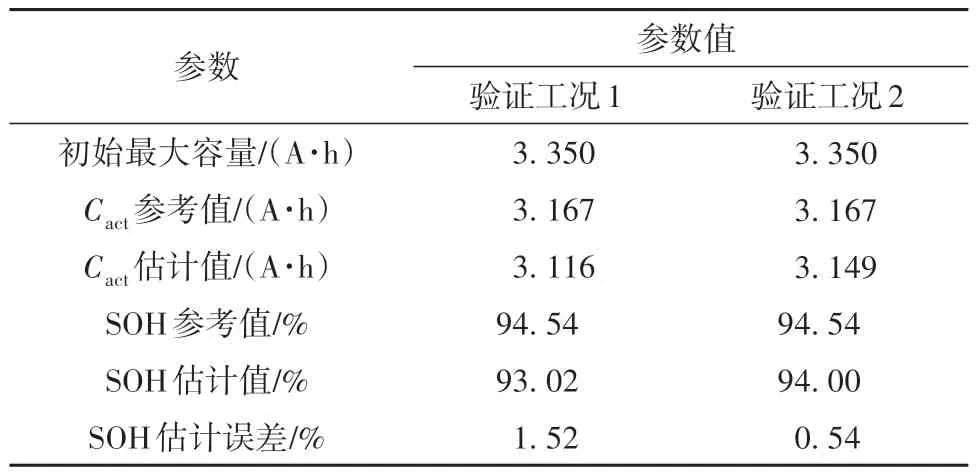
表2 两种验证工况下SOH的估计结果及误差Table 2 Estimation results and errors of SOH under two work⁃ing conditions

为进一步说明文中提出的估计方法的优势，以SOC 为例进行图示和分析，将文中方法与EKF估计算法进行对比，结果如图12 所示。可以看出，两种算法的估计曲线趋势相似，都较好地贴合了SOC参考值，但文中提出的状态联合估计方法具有更高的估算精度和更好的估计稳定性。这是因为，与DAEKF 算法相比，EKF 算法缺乏对噪声的自适应功能，在应对环境噪声、传感器采样率限制及测量缺陷等因素带来的干扰时，无法进行自适应匹配，所以对SOC的估计稳定性更差，最大误差超过2.5%。

图12 EKF算法与DAEKF算法的SOC估计结果对比Fig.12 Comparison of SOC estimation results between EKF and DAEKF algorithms

SOE 的对比结果与SOC 的类似，此处不再赘述。两种算法的SOC、SOE和SOH的最大估计误差见表3。

表3 EKF与DAEKF算法的最大估计误差对比Table 3 Comparison of maximum estimation error between EKF and DAEKF algorithms

由上述验证结果可知：文中提出的基于DAEKF 算法的多时间尺度主要状态在线联合估计方法能够有效地应用于NVR18650B 型锂离子电池的3个主要状态的在线联合估计；并且，与EKF算法相比，该方法在不同的验证工况下都能够实现三元锂离子电池SOC、SOE和SOH的精准估计，其中SOC 和SOE 的估计误差均保持在1%以内，SOH 的最大估计误差为1.52%，说明该算法具有较高的精度和在线估计收敛稳定性。

4 结论

文中针对三元锂离子电池主要状态的在线联合估计问题，为适应由不确定噪声、传感器采样率限制和测量缺陷带来的扰动，提出了一种基于DAEKF 算法的多时间尺度三元锂离子电池主要状态在线联合估计方法。在二阶RC 模型基础上构建DAEKF 算法的状态空间方程，通过FFRLS 进行在线参数辨识，实现对三元锂离子电池的荷电状态、能量状态和健康状态这3 种主要状态的在线联合估计。

实验验证及与EKF 算法结果的对比表明，文中提出的在线联合估计方法具有更高的估计精度。在1C 满放满充的验证工况下，SOC 和SOE 的估计误差均小于1%，SOH 的估计误差小于1.6%；在脉冲测试的在线验证工况下，SOC、SOE 和SOH 的估计误差均保持在1%以内，说明文中方法具有较高的估计精度及较好的在线估计收敛稳定性。

综上，文中提出的基于DAEKF 算法的多时间尺度主要状态在线联合估计方法能够有效地进行三元锂离子电池的SOC、SOE 和SOH 这3 种主要状态的在线估计，且估计误差均保持在1.6%以内。后续可以将此方法集成于电动汽车电池管理系统，基于实时采集的数据，实现三元锂离子动力电池主要状态的在线实时联合估计，从而为车载动力电池状态检测及动力电池梯次利用等应用场景提供一定的参考，并推广至其他类型的电池。