一种小型码垛机械臂刚柔耦合动态特性分析
2023-03-14林红刚袁锐波陈有锦
林红刚,袁锐波,罗 威,陈有锦,朱 正
(1.昆明理工大学 机电工程学院, 昆明 650504;2.光机电液系统集成与控制研究所, 昆明 650504)
0 引言
当今世界,经济全球化成为时代趋势,科技的迅速发展,导致国际竞争日益加剧,世界各国都在努力发展经济。在国家新一轮工业产业升级的背景下,对许多大型港口的吞吐量提出了更高的要求,码垛机器人作为港口装卸货的重要设备之一,国内对其控制算法从未停止研究,但是针对码垛机器人工况位姿的研究较少[1]。
目前国内对码垛机器人的仿真研究主要从以下方面进行:简化机器人机构在Matlab或者ADAMS软件中进行运动控制和算法分析、对设计的机器人在ANSYS或者ADAMS软件中进行主要部件的刚性分析、对机器人的关键部件在ANSYS和ADAMS软件中进行刚柔耦合联合仿真分析。可以发现国内对码垛机器人的仿真研究渐入佳境,但是针对码垛机器人在软件中进行独立刚柔耦合的工况位姿研究较少。
基于此,本文结合企业生产线的装载卸货的工位需求,拟设计一种小型的码垛机械臂结构,通过在ANSYS软件中对该机器人在不同工况下进行静力学与刚柔耦合的对比分析,并分析其运动特性,对机械臂的使用寿命进行下一步的计算具有一定的意义。
1 机械臂的结构及工作原理
根据各行业对机械臂的使用情况,机械臂主要对产品进行转移,对机械臂的位姿有极高的需求,参考生产线上的具体工作情况,对工作的位姿进行分析,设计了一种小型的机械臂结构。
本文设计的小型机械臂主要由6部分构成[2]。分别是:底座、腰部、小臂、大臂、末端执行器和电机。其具体的组成结构见图1。

图1 机械臂的组成结构示意图
机械臂具体的工作流程为:
1) 底座固定在移动设备上,设置工作参数;
2) 启动底座电机,腰部零件在底盘和腰部传动系统作用下绕底座轴线开始旋转运动;
3) 通过腰部电机与小臂驱动电机可使末端执行器达到机械臂运动空间内的目标位置,机械臂末端执行器最终将产品传递到目标位置上。
本机械臂适用于当自动化生产线上产品运输或者生产结束时,由机械臂将产品转移和堆放到指定位置。
2 机械臂的运动学模型及位姿空间选取
2.1 机械臂的运动学模型
机器人运动学主要是通过对关节与构成机器人的各个刚体之间的运动关系进行研究。常用的机器人运动学描述方法有D-H参数法与指数积公式法[3];D-H法作为一种经典的操作臂建模方法,它是关节空间向位姿空间转换的桥梁,是解决串联机器人运动学建模问题的重要工具,现已成为现代工业中串联机器人的主流建模方式。
故本文通过D-H参数法来获得机械臂的运动学模型。要想推导机械臂关节空间到位姿空间的变换,首先要建立相应的机械臂的连杆坐标系,所需机械臂的连杆坐标系如图2。

图2 机械臂连杆坐标系示意图
参考文献[3-4],有机械臂连杆的坐标变换阵的通用算式:
(1)
式(1)中的各个参数所表达的含义如表1所示。

表1 参数定义
结合图2所示的机械臂和表2的参数,通过将各个参数导入式(2)可以得到各个关节的转换矩阵,同时得到任意坐标系的姿态。

表2 机械臂连杆参数
表中d1=210 mm;d2=245 mm;d3=1 280 mm;d4=1 365 mm;d5=125 mm。
关节转换矩阵公式:
(2)
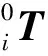
(3)
(4)
(5)
(6)
(7)
其中:ci、si分别代表cosθi、sinθi,i=1,2,…,5。
由以上矩阵可得其相对于基坐标系的位姿矩阵:
(8)
(9)
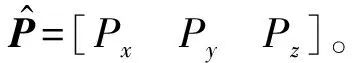
2.2 工况位姿的选取
通过市场调研[5-7],采用Q235号钢作为机械臂材料,在机械动力学中,不同的转角组合对设备模型影响程度是不一样的,针对其不同工况位姿的要求,对以下3种基本位姿进行了研究。
1) 位姿1:机械臂的腰部绕底座旋转90°,大臂绕腰部旋转-30°,小臂绕大臂旋转25°,到达左右工位。
2) 位姿2:在位姿1的基础上,机械臂的腰部绕底座旋转60°,大臂绕腰部旋转-15°,小臂绕大臂旋转50°,到达近点工位。
3) 位姿3:机械臂的腰部绕底座旋转30°,大臂绕腰部旋转-30°,小臂绕大臂旋转50°,到达远点工位。
3 ANSYS静力学分析
3.1 机械臂模型的假设
对于绝大部分的码垛机械臂结构而言,它们的结构非常复杂,为了研究机械臂在整个过程中的主要受力情况,本文对机械臂模型作了一些简化与假设。在ANSYS中对模型做了如下假设[8-11]:
1) 对机械臂内未参与传动的零部件进行Form New Part操作;
2) 忽略模型的尺寸公差及装配误差;
3) 在机械臂的刚柔耦合模型中仅将机械臂大臂进行柔性化,其余的零部件设为刚体。
3.2 ANSYS静力学仿真
在ANSYS的Static Structural项目里的Engineering Data设置好机械臂各部件需要的材料参数,各构件材料采用236钢,在 Engineering Data 中设置材料密度为7 850 kg/m3,泊松比为0.3,杨氏模量为2.1×105MPa;然后在Geometry中导入模型并进行假设1的设置,接下来在Model中进行假设3的设置,然后进行材料的添加,对其进行网格划分。
在完成约束设置后便可对机械臂添加驱动[12-16],在Model模块里创建所有连接,固定约束1个,旋转副3个,接触形式为摩擦接触摩擦因子取0.2,机械臂在整个运行周期内,始终受到地球重力的作用,参数为9.8 m/s2,方向负Z轴。同时将其运动过程划分为启动、平移、举起、取料4个阶段分析;通过角度驱动的方式进行4个阶段的设置,得到如图3所示的机械臂的刚柔耦合动力学模型的约束设置。
3.3 结果分析
在上述约束条件下进行静力学分析,求解后得到3个位姿工况全程最大等效应力值分别为 5.358 2、4.938 4、5.085 8 MPa,如图4所示。出现在大臂和底盘连接部位。根据要求安全系数一般取1.5,根据大臂的安全系数N=σb/σmax,求得N1=44.045,N2=47.79,N3=46.404,完全符合要求。

图3 机械臂模型的静态约束设置示意图
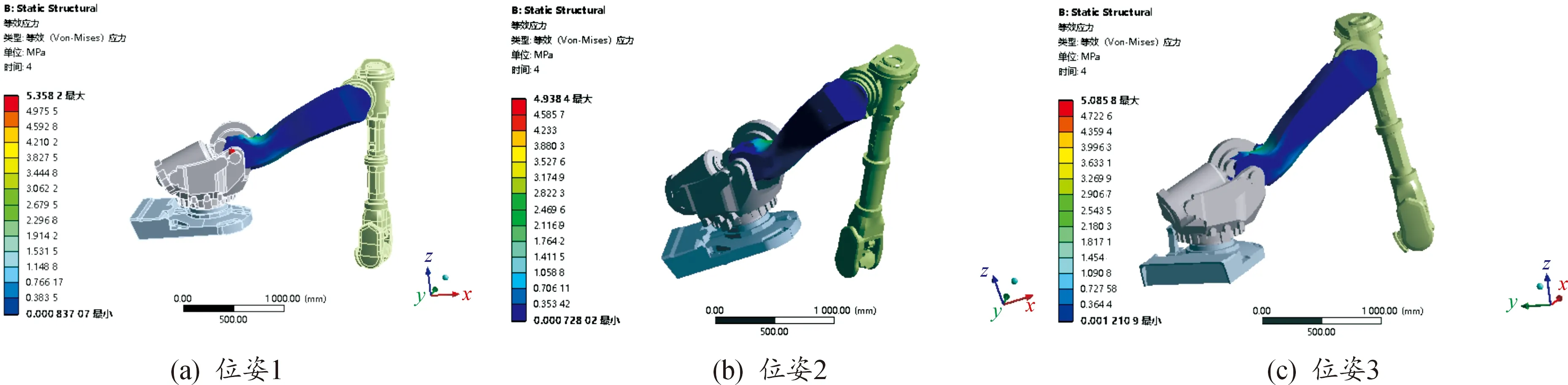
图4 静态应力云图
4 ANSYS刚柔耦合动力学分析
4.1 机械臂模型的建立方式
有很多方式可以建立用于刚体动力学模型,比较常见的刚柔耦合分析步骤:先在ANSYS软件对柔性体进行网格划分后保存为.mnf文件,导入ADAMS软件替换原来刚性的部件,然后进行约束驱动以及求解的设置[17-21]。本文刚柔耦合瞬态动力学分析通过ANSYS软件进行分析,考虑到机械臂模型结构的复杂性,为了减少多个软件之间导入导出的误差,直接在动力学仿真软件ANSYS中,导入SolidWorks中的刚体动力学模型,具体模型如图5所示。
4.2 工况的仿真设置
在ANSYS的Transient Structural项目里的Engineering Data设置好机械臂各部件需要的材料参数,然后在Geometry中导入模型并进行假设1的设置,接下来在Model中进行假设3的设置,将机械臂的大臂设置为柔性材料,将其余部件设置为刚性材料,然后进行材料的添加,对其进行网格划分,共生成 156 148个网格,106 616个节点如图6。
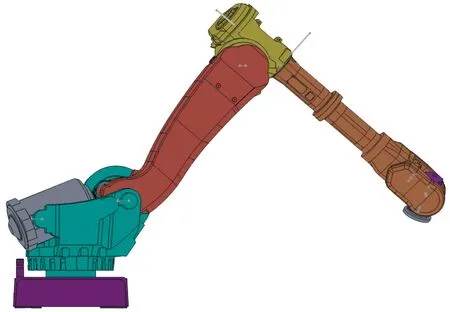
图5 机械臂装配模型示意图

图6 大臂的有限元网格划分示意图
在完成约束设置后便可对机械臂添加驱动在Transient Structural 模块Model里创建所有连接,设置情况与3.2小节一致;得到如图7所示的机械臂的刚柔耦合动力学模型的约束设置。
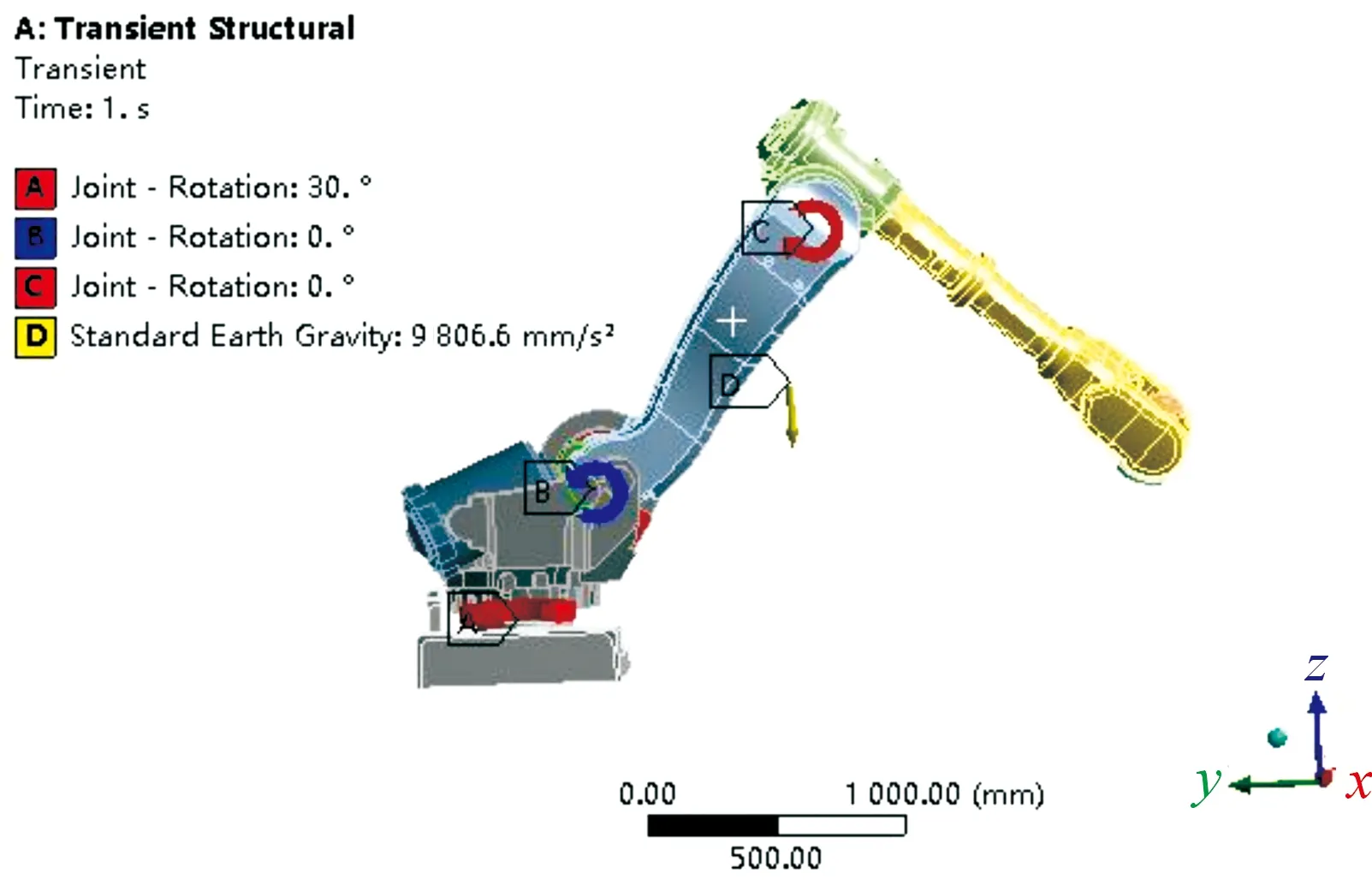
图7 机械臂模型的约束设置
设置仿真分析时间为4 s,最小步长为0.01 s,通过上述对约束及驱动的设置,便可对机械臂进行仿真。
4.3 结果分析
在ANSYS软件中按照上述步骤,对比静力学分析,分别得到3种位姿下的等效应力图,如图8所示。在约束条件下进行静力学分析,求解后得到3个位姿工况全程最大等效应力值分别为19.15、16.05、18.494 MPa。出现在大臂和底盘连接部位。大臂的安全系数N=σb/σmax,求得系数分别为N1=12.324,N2=14.704,N3=12.760,安全系数取1.5,也完全符合要求。
与静力学分析结果对比,静力学分析的等效应力结果与瞬态动力学的结果偏差很大,可以发现采用瞬态动力学分析所得到的结果对安全的评估更为精确。

图8 静态应力云图
4.4 运动特性分析


图9 大臂的受力曲线
从图9可以看出在相同时间内位姿1的应力最大值滞后于位姿2和3,且出现2个峰值,最后趋于稳定。
图中可以分析出第一个峰顶是机械臂底盘电机工作时出现,分别为72.199、50.034、25.878 MPa,第二个峰顶是在大臂工作时出现分别为82.941、57.74、28.898 MPa,数据结果表明,机械臂进行作业时,大臂受力最大,在机械臂空间运动情况下,机械臂最容易发生故障。
同时也可以求得机械臂3个位姿工况下的大臂的应力安全系数N=σb/σmax,求得为Nmin=σb/σmax=236/82.941=2.845 4,安全系数取1.5,机械臂仍然满足材料的要求。
对比采用最大等效应力进行分析,在瞬态动力学分析中,应力最大值为82.941 MPa,与最大等效应力19.15 MPa差值极大。因此,从安全的角度来看,采用全过程的最大应力分析的方法更为精确有效。
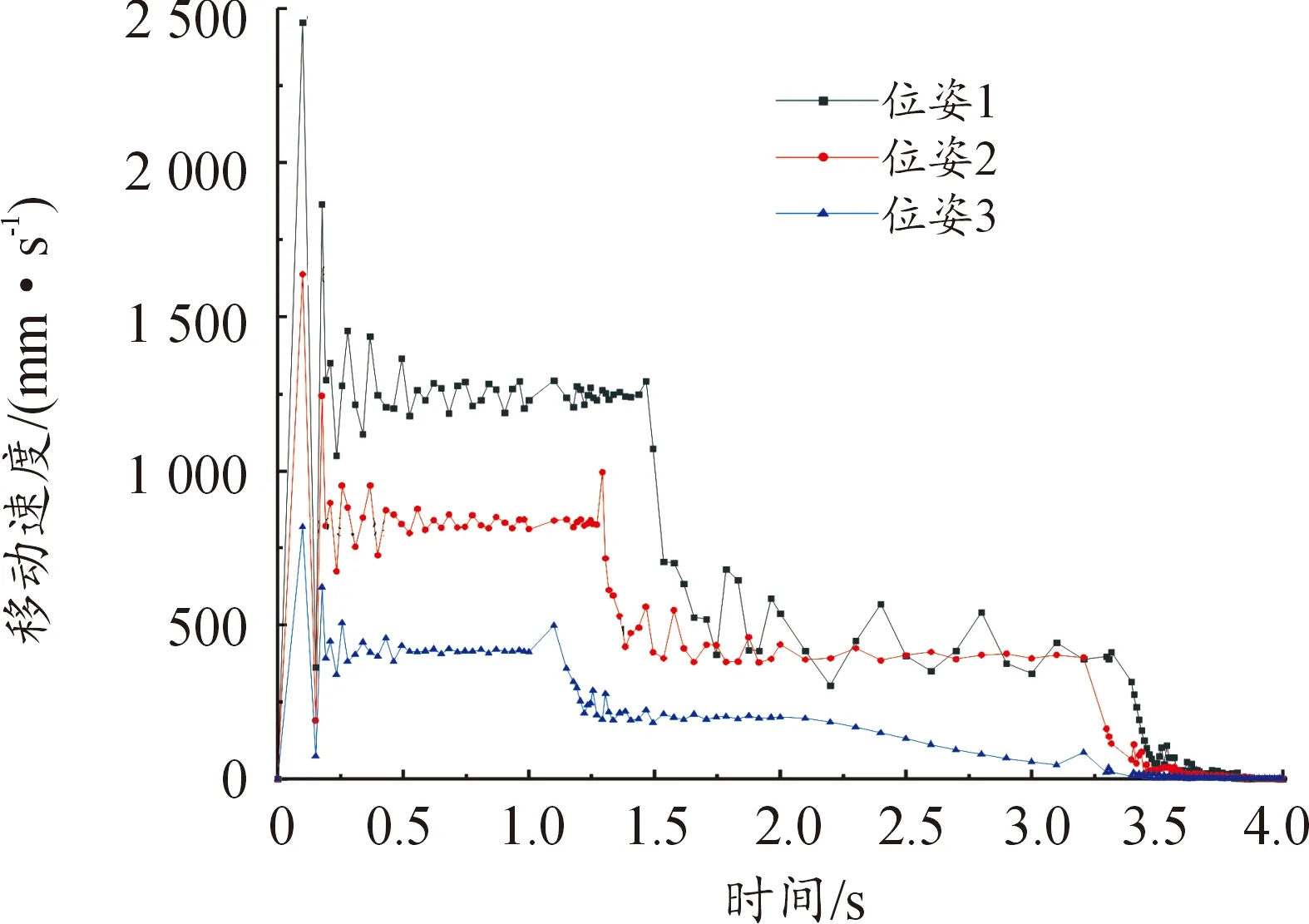
图10 大臂的速度曲线
从图10可以看出,在相同时间内,位姿1的速度最大值滞后于位姿2和3,随着工作时间推移,最后趋于稳定。
图中可以读出3个位姿的速度峰值分别为2.455 1、1.637、0.819 24 m/s,且达到速度峰值的时间几乎是同一个时间节点0.25 s,随着时间推迟,大臂移动速度波动逐步趋于稳定,并且由于速度峰值越大,速度波动越大,趋于稳定的时间越慢。这说明速度移动峰值对大臂的移动稳定性影响较大。

图11 大臂的位移曲线
从图11可以看出,在相同时间内,位姿1的位移拐点值滞后于位姿2和3,随着工作时间推移,最后趋于稳定。同时可以得出,机器人在3种位姿下的最大工作范围为1 372.7 mm。由此可以进一步对码垛生产线机器人安装位置进行设计。
5 结论
1) 与传统的刚柔耦合分析方法相比,本文所采用的设计思路减少了软件之间模型转换的过程,减少了设计周期的时间成本和软件之间模型转换的影响误差。
2) 仿真数据和计算表明:当采用静力学刚性分析结果精度低,同时采用最大等效应力来分析并不能准确判断其结构的安全;在一定时间内,速度移动峰值会极大影响大臂的移动稳定性。
3) 通过对比3种工作情况的位姿和最大应力小于材料的屈服强度。且在3种位姿下能达到 1 372.7 mm的工作范围,本文设计的小型机械臂在进行作业时,满足工业设计的要求。
4) 考虑到动力学模型输出特性对接触刚度非常敏感,一般来说,接触刚度设置为0.01~1,对输出结果影响较小,为了提高计算效率,本文仅作常规设置,对接触刚度与输出特性的关系有待进行深入探究。
