输电塔钢管涡激振动控制措施的风洞试验研究

2023-03-13黄铭枫

空气动力学学报 2023年2期

夏谦，杜海，冯衡，高彬，黄铭枫，*

(1.中国电力工程顾问集团中南电力设计院有限公司，武汉 430071；2.浙江大学建筑工程学院结构工程研究所，杭州 310058)

0 引言

钢管塔是被广泛应用于特高压输电线路中的一种塔型。钢管输电塔具有承载力高、稳定性强、受力均匀且承受风荷载相对较小的特点，在我国“西电东送”、“北电南送”等长距离特高压送电工程中发挥着至关重要的作用。然而钢管塔中一些长细比较大的钢管构件，特别是趋于水平布置的构件，在低风速下容易发生横风向的涡激振动[1-2]。长期高频、大幅度的涡激振动容易造成钢管节点螺栓连接松动、脱落甚至是构件的疲劳破坏，严重威胁着特高压输电线路的安全运营和维护。

许多学者提出了不同的涡激振动控制措施，包括主动控制和被动控制措施。汤爱平等[3]研究了基于主动吸气的圆柱涡激振动控制措施，通过在圆柱表面布置吸气孔来改变局部流场的分布，但抑振效果最大仅为70%。Wang 等[4]分析了合成射流参数与抑振效果的关系。陈威霖等[5]通过在主圆柱周围增加旋转小圆柱来实现主圆柱的抑振，并在研究了控制角度、间隙比、旋转角速度、旋转方向、阻尼比几个参数影响的同时，进行了参数优化，确定了最优参数组合。

相比于主动控制，被动控制措施的成本更低、实用性更强，相关研究更为广泛。涡激振动被动控制措施大致可以分为整流罩[6-7]、分离盘[8-9]、扰流板[10-11]、螺旋列板[12-13]、控制杆[14-15]等。其中，扰流板是一种由数个肋板组成的扰流装置，能够扰乱结构局部流场的规律涡脱从而抑制涡激振动的发生。Zhang 等[16]通过风浪流水槽试验研究了月牙形扰流板对海洋立管涡激振动的抑制效果，试验中研究了7 种不同的扰流板布置形式，但其中只有两种形式能达到70%以上的抑振率。Gu 等[17]设计了一种可自由旋转的片状扰流板用于圆柱体涡激振动的控制，试验中扰流板最高能够减小96%的气动升力。Liang 等[18]采用柔性扰流板对圆柱涡激振动进行控制，试验结果表明其控制效果与扰流板的长径比有关，而当长径比过大时，圆柱则会出现舞动现象。

针对特高压输电塔钢管构件涡激振动控制的相关研究较为缺乏，部分研究表明输电塔钢管的节点型式对其涡激振动的特性具有较大的影响[19-20]。但目前学者们基本采用的是基于结构无限长假定的气动弹性节段模型，并未考虑真实节点连接型式的影响。在扰流板研究方面，研究对象大多是某种单一型式的扰流板，缺乏不同型式和布置情况对钢管涡激振动控制的参数化研究。如何利用扰流板对输电塔钢管涡激振动实现经济有效控制的优选分析也相对欠缺。

本文考虑了输电塔钢管的具体节点型式，进行了C 型节点钢管的风洞试验，验证了文献[21]中提出的输电塔钢管涡激振动幅值预测公式。进一步研究了扰流板外形、间距、长度和肋高等设计安装参数对钢管涡激振动的控制效果，并综合材料、安装成本和抑振效果对不同设计参数下扰流板的性价比进行评估，最后基于帕累托最优解法选取了考虑成本后的扰流板最优设计安装方案，给出了工程应用建议。

1 临界风速和涡振幅值计算

不少国内外学者[22-24]提出了半经验公式来计算确定圆柱体涡激振动的临界风速和涡振幅值，但这些公式大多没有考虑钢管节点型式对涡激振动的影响。C 型节点（如图1（b）所示）在钢管输电塔中有着广泛的应用。Huang 等[21]基于足尺风洞试验，针对输电塔C 型节点支承钢管提出了涡激振动临界风速和最大幅值的计算公式。其中，C 型节点支承钢管涡激振动临界风速可计算如下：

式中：λ为钢管的长细比；E为钢管的弹性模量，取值2.06×1011N/m2；ρ为钢管的密度，取值7 850 kg/m3；St为斯托罗哈数，当雷诺数在亚临界范围内时可以近似取值0.2[25-26]。

C 型节点支承钢管涡激振动最大位移的预测公式为：

式中：y为钢管横向位移；D为钢管的直径；L为钢管的长度；ρa为空气密度，取值1.25 kg/m3；γ为模态归一化系数；ψ(x)为结构的模态函数；c为阻尼系数，通过对C 型节点钢管试验数据进行拟合得到，取值5.79 kg/s。

对于C 型节点钢管，假设边界条件为简支，其一阶模态函数可以表示为：

将公式（4）代入公式（3），得到模态归一化系数γ为1.274。

对于其他节点型式的钢管，γ根据模态函数不同需重新计算；钢管阻尼、刚度受节点型式影响，其阻尼系数c需要进一步通过试验确定。

2 风洞试验

风洞试验在浙江大学ZD-1 风洞实验室进行，ZD-1 边界层风洞为单回流闭口立式结构，试验段长18 m、宽4 m、高3 m；风洞的最高风速55 m/s。试验选用均匀流场作为测试风场。如图1（a）所示，在风洞实验室两侧布置有两根刚性立柱，试验钢管通过两端的C 型节点板与立柱进行连接固定。试验钢管为Q345 钢，直径D为63.5 mm，壁厚为4 mm，长度为3 125 mm，长细比为151。

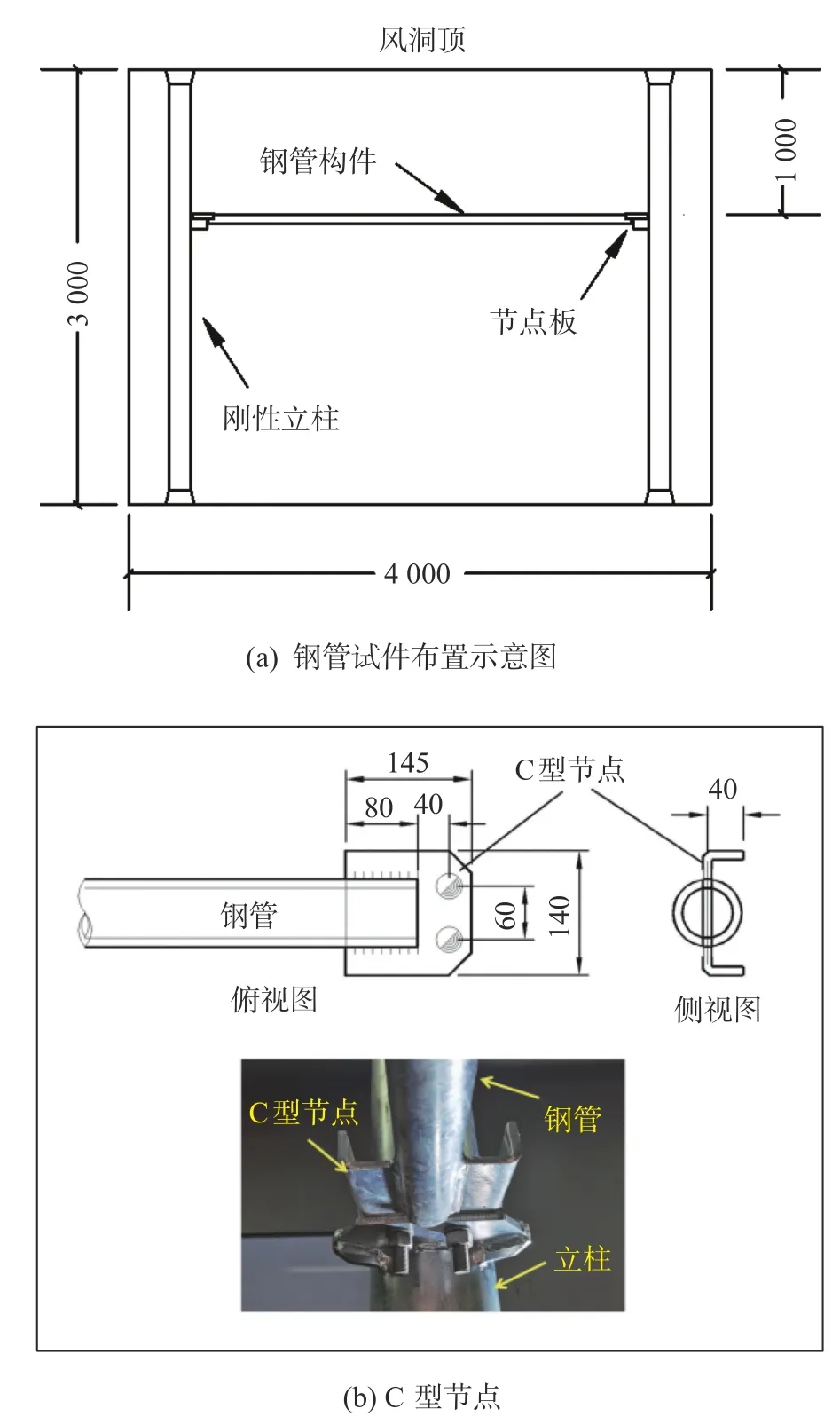
图1 钢管模型风洞试验Fig.1 Experimental setup of the wind tunnel test

根据公式（2）计算得到该钢管试件涡激振动临界风速为6.018 m/s。钢管涡激振动的试验风速设置为3～8 m/s，风速间隔为0.5 m/s。试验中同步采用加速度传感器和计算机视觉方法[27]来测量钢管的加速度和位移响应，如图2 所示，每种工况下的数据采集时间为60 s。加速度传感器型号为Kistler 8640A50，采样频率2 048 Hz，量程±50 g，灵敏度100 mV/g。

采用的计算机视觉识别技术主要由工业相机和计算机软件系统组成，通过识别设置在钢管跨中背风侧的位移标志物，结合计算机图像识别算法来提取目标位移信息。其精度主要取决于图像的大小，本次试验拍摄的图像大小为128 pixel × 128 pixel，如图2（b）所示，其中50 pixel 对应实际30 mm 的长度，再利用双抛物线拟合法亚像素技术，使定位分辨率提升至0.02～0.05 pixel，理论上能够实现0.03 mm 的测量精度。

图2 基于计算机视觉技术的位移测量Fig.2 Displacement measurement based on computer vision-based method

根据Stansby 和Pinchbeck 对“十”字型扰流板的研究[28]，当扰流板肋高和宽度为D/3、布置间距为2D/3 时，扰流板的抑振率可达70%。本文试验中扰流板为Q235 钢，采用无量纲化的设计，主要考虑了扰流板间距、长度、肋高和外形的影响，不同型式的扰流板的设计如图3（a）所示，扰流板沿钢管等间距布置，以工况2 为例，布置图如图3（b）所示。试验中共研究了5 种不同外形的扰流板，其中型式1 具有8 根肋板且呈“米”字型，型式2、4、5、6 具有4 根肋板且呈“十”字型，型式3 具有4 根肋板且呈“X”型，型式7 和型式8 分别为在型式1、型式2 的基础上，使肋板倾斜了45°，扰流板厚度均为0.03D。扰流板设计参数与试验工况如表1 所示。

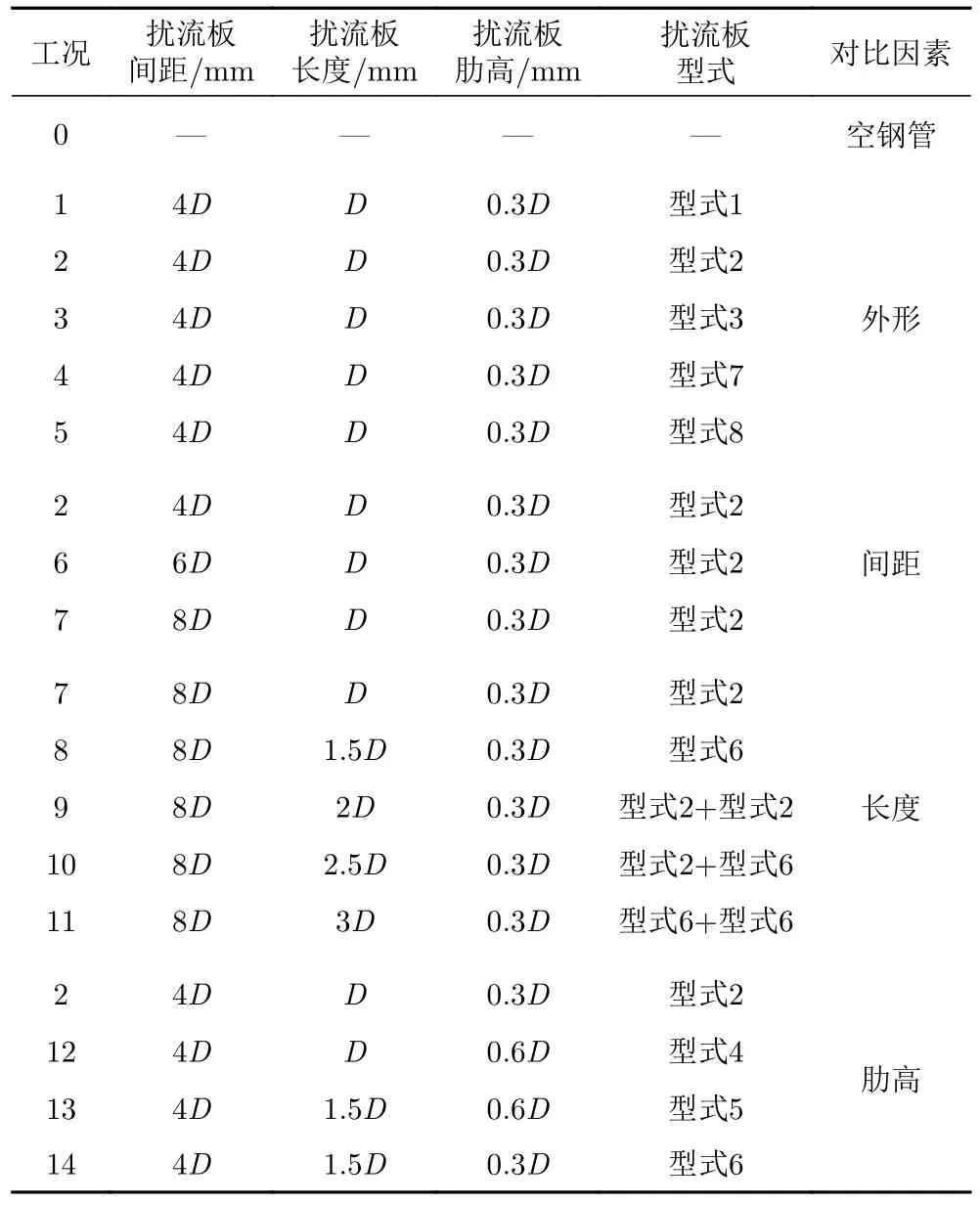
表1 扰流板参数与风洞试验工况Table 1 Design parameters of spoilers and conditions of wind tunnel test

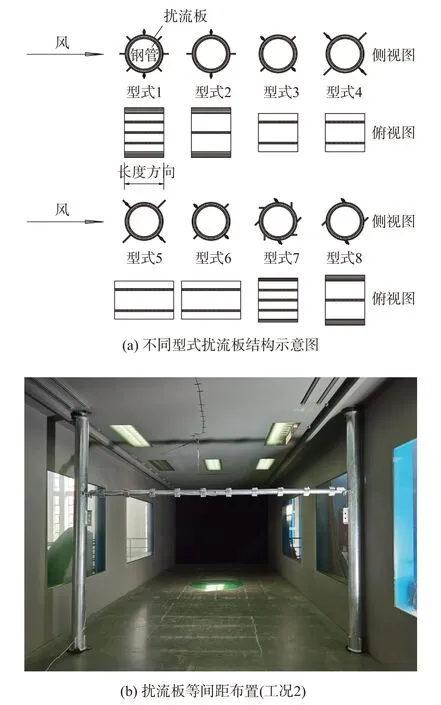
图3 不同型式的扰流板的设计与试验布置Fig.3 Design and experimental setups of different types of spoilers

3 试验结果分析

3.1 涡激振动的预测

试验钢管在不同风速下的最大位移如图4 所示，可见当风速在3～8 m/s 的区间内时，钢管的最大位移随着风速的增加先增大后减小。当风速小于5 m/s时，钢管的最大位移值变化不大，均在0.1 mm 以内；当风速大于5 m/s，涡振幅值迅速增大，在6 m/s 时出现峰值为0.803 mm，最大位移均方根值为0.370 mm，此时钢管的位移时程如图5 所示。当风速继续增加，涡振幅值又迅速减小并降至0.2 mm 以下。在0.5 m/s风速间隔下，风洞试验捕捉到钢管在风速6 m/s 时发生涡激共振，故试验确定临界风速为6 m/s。

图4 不同风速下钢管的最大位移Fig.4 Maximum displacement of steel tube under different wind speeds

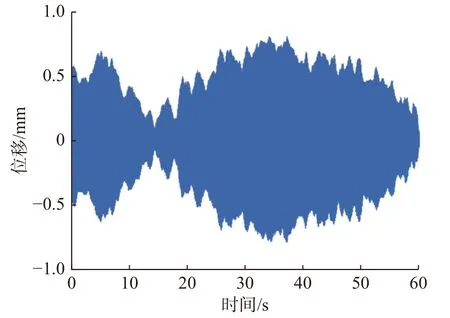
图5 钢管试件在临界风速下的位移时程（6 m/s）Fig.5 Displacement time history of the steel tube at VIV critical wind speed 6 m/s

表2 给出了钢管涡激振动的预测值与试验值，根据公式（1）预测得到的钢管临界风速为6.018 m/s，与试验值6 m/s 较为吻合。根据公式（2）预测得到的钢管跨中最大位移为0.987 mm，试验值为0.803 mm，公式（2）略微高估了钢管涡激振动的最大振幅，但总的来说两者相差不大，预测值具有较高的参考价值。结果表明，公式（1）和公式（2）能够较好地预测C 型节点钢管涡激振动的临界风速与最大幅值。

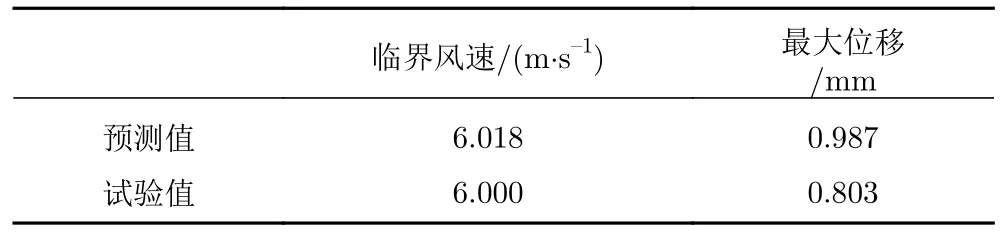
表2 钢管涡激振动的预测值与试验值Table 2 Predicted value and experimental value of VIV

3.2 涡激振动的抑制

试验中涡激振动抑振率的定义如下：

式中，η为抑振率；Yb为无扰流板钢管的风致响应均方根；Yd为钢管安装扰流板后的响应均方根。抑振率越高说明扰流板的减振效果越好。

3.2.1 扰流板外形影响

图6 给出了不同外形的扰流板对钢管涡激振动的抑振率。相比于型式1、3、7，型式2、8 的抑振效果相对较好。型式2、8 的扰流板的抑振率均超过了95%，而型式1、3、7 的扰流板的加速度抑振率均未达到85%，位移抑振率均小于80%。

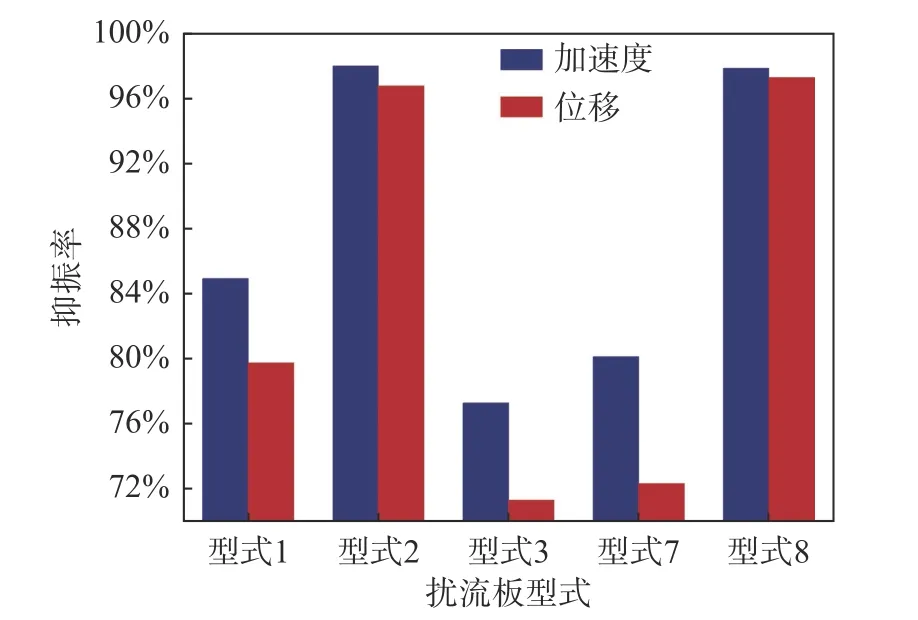
图6 不同外形扰流板的抑振率Fig.6 VIV suppression rate of spoilers with different configurations

上述结果表明，扰流板的外形对于抑振率的影响较大。当分别采用型式1、2、3 的扰流板时，抑振效果型式2＞型式1＞型式3，对应不同肋板外形下的抑振效果为“十”字型＞“米”字型＞“X”型，“十”字型扰流板的抑振率比“X”型扰流板高出约20%。对比肋板倾斜前后的试验结果可知，当“十”字型肋板倾斜45°后，抑振率变化不大，当“米”字型肋板倾斜45°后，抑振率减小约5%，可见肋板倾斜带来抑振率的改变程度小于肋板外形的改变。

对比“十”字型、“X”型和“米”字型扰流板，“十”字外形的扰流板对钢管涡激振动的控制效果最好，“米”字型次之，“X”型效果最差。且将肋板倾斜45°后，对抑振率的提升不明显，反而会有所降低。

在亚临界范围内，发生涡振时旋涡的分离点位于钢管上下两端附近[29]，“十”字型扰流板的上下肋板会干扰分离点附近的气流，从而避免旋涡进行规律的脱落。“X”型因为肋板位于45°的位置，对涡脱的抑制程度没有“十”字型好；“米”字型肋板沿环向布置较密，对钢管气动外形改变不大，仍然呈类似圆形的钝体，抑振效果不及“十”字型扰流板；肋板倾斜后使肋板沿径向的有效长度减小，且肋板倾斜后钢管气动外形更接近圆形，从而对旋涡脱落的干扰效果有所下降。

3.2.2 扰流板间距的影响

如表3 所示，对于型式2“十”字型扰流板，无论间距为4D、6D还是8D，其抑振率基本可达到90%以上，表明有较好的抑振效果。总体而言，扰流板布置越密抑振效果越好，究其原因在于密布的扰流板破坏了钢管表面旋涡脱落沿长度方向的相关性，从而起到抑振的效果，布置越密，对单位长度钢管气动外形改变越大。当扰流板间距由8D减小至6D，抑振率由90%左右增长至96%左右；当扰流板间距进一步减小至4D，抑振效果提升幅度趋于减小，抑振率提升不到2%。

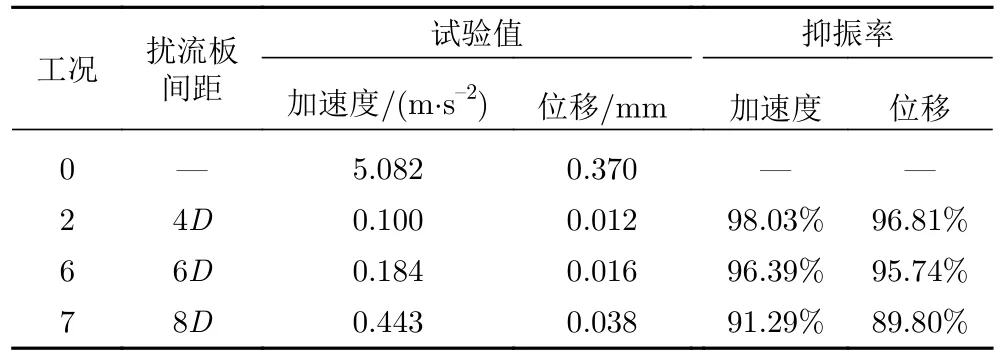
表3 不同扰流板间距下的抑振率Table 3 VIV suppression rate of spoilers with different spacings

3.2.3 扰流板长度的影响

如图7 所示，随着扰流板长度的增加，抑振率先是大幅增加，然后趋于稳定。当扰流板长度大于1.5D时抑振率基本在96%以上，而扰流板长度为1D时的抑振率相对较低，约为90%。相比于位移抑振率，扰流板的加速度抑振效果更好，加速度抑振率基本在97%以上，扰流板长度为2.5D时最大为97.4%。位移抑振率则在扰流板长度为2D时达到最大。改变扰流板长度与调整间距的抑振机理类似，均通过改变钢管气动外形的同时破坏钢管表面旋涡脱落沿长度方向的相关性来抑制规律涡脱的发生。

图7 不同扰流板长度下的抑振率Fig.7 VIV suppression rate of spoilers with different lengths

3.2.4 扰流板肋高的影响

如表4 所示，本文研究的0.6D和0.3D两种肋高的扰流板均能够实现较好的抑振效果，位移抑振率均超过了95%。在工况2 与工况12 扰流板长度为D的情况下，肋高为0.3D时的抑振效果要更好；在工况13 与工况14 扰流板长度为1.5D的情况下，肋高为0.6D时的抑振效果更好，抑振率均大于96%，相比之下，0.3D肋高时的加速度抑振率较低，约为88%。从抑振机理看，肋板越长，对分离点附近旋涡的干扰效果越明显，抑振效果要更稳定。总体而言，扰流板肋高为0.3D时的抑振效果即可满足工程上的要求。

表4 不同扰流板肋高下的抑振率Table 4 VIV suppression rate of spoilers with different heights

4 方案优选

4.1 考虑成本的扰流板抑振效果分析

综合考虑扰流板成本，对安装外形为“十”字型扰流板下的10 种方案进行抑振效果分析。结合实际制作安装费用和材料成本，取钢材密度为7 850 kg/m3，钢材价格为5 000 元/吨，扰流板的人工制作安装费为50 元/个进行计算评估。各方案下的扰流板基本信息如表5 所示。

表5 扰流板基本信息Table 5 Basic information of spoilers

为综合考虑抑振效果，取平均抑振率为各方案下位移抑振率和加速度抑振率的平均值，记为。考虑扰流板各项费用后得到各个方案的总成本与对应的抑振率大小如表6 所示。从表6 可以看出，10 种方案的平均抑振率均达到90%以上，方案1 抑振效果最好，平均抑振率达到97.42%，但此时总成本较高；方案4 总成本最低为207.85 元，但抑振率未达到97%，抑振效果不及方案1。综合分析10 种方案可知，成本与抑振率无法同时达到最优，需进行多目标优化。

表6 10 种方案的成本与效益Table 6 Costs and benefits of 10 options

4.2 基于帕累托最优方法的最优方案

在对扰流板进行优化设计时，需要同时实现两个目标：一是抑振率高；二是总成本低，总成本包含材料成本和安装成本。为进行最小化双目标优化，记平均抑振率的倒数1/为 η0，此时优化目标为 η0与总成本均要最小。4.1 节分析表明上述方案均无法使成本与效益同时达到最优，该多目标优化问题可通过帕累托最优理论进行分析。

对于n个目标最小化多目标优化问题可表述为：min{f1(x),f2(x),···,fn(x)}，其中fk(x)为该问题的多个目标函数。根据帕累托最优理论，对于该问题的解若满足以下两个条件：

则称解x0支配解x，若x0不被其他任何解所支配，则x0为该问题的一个帕累托最优解，最优解往往不止一个，所有的帕累托最优解组成的集合为帕累托前沿，对于双目标优化问题，帕累托前沿为一条曲线。

以 η0为纵坐标，总成本为横坐标，将表6 中10 个方案的成本与效益的数据点绘于图8 中，各方案的总成本与抑振效果的关系如图8 所示。

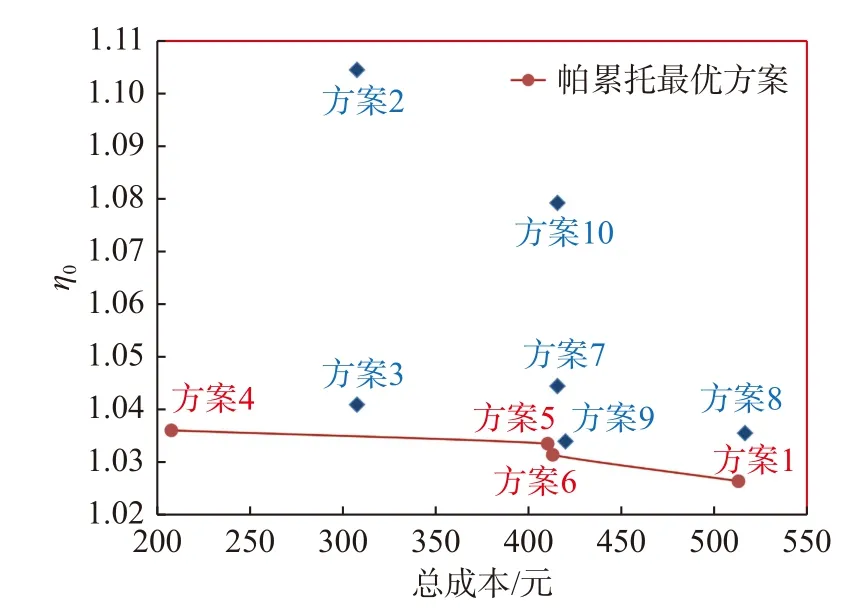
图8 帕累托最优方案Fig.8 Pareto Optimal Solution

从图8 中可知，方案1、方案4、方案5、方案6 对应的点互相不支配，且不被其他点支配，为上述方案中的帕累托最优解。连接四个帕累托最优解得到帕累托曲线，该曲线较为平坦，表明上述四种帕累托最优方案的抑振效果差别不大。方案1 能使抑振率达到最大，但总成本最高；方案4 的总成本最小但抑振效果要弱于其他三个方案。设计者可根据具体需求进行方案的选择。