地震作用下桥梁结构多点碰撞影响参数研究

肖 恒

（重庆三峡学院，重庆 404000）

0 引言

桥梁结构的相邻梁体因各自存在的动力特性差异，在地震激励下其动力响应不同，从而产生相邻梁体位移不同步的现象。当相邻梁体的相对位移大于桥梁伸缩缝的距离时，便会发生碰撞。碰撞会在极短时间内对梁体产生巨大的冲击荷载，造成梁体开裂、位移、支座破坏等，是引起桥梁破坏倒塌的主要原因。

数值模拟仿真分析是研究桥梁碰撞响应的重要手段。目前，已有众多学者采用数值分析方法对桥梁的碰撞响应问题展开了研究，也取得了不错的成果［1-4］。相关研究表明，整个碰撞过程的发生时间都非常短，其碰撞物理行为复杂，形式多样，并且在伸缩缝的碰撞形式中，不仅有横向的摩擦碰撞，也存在纵向的不均匀碰撞，这使得对桥梁在地震荷载下的碰撞问题进行计算变得十分困难［5］。因此在开展桥梁结构的数值仿真分析时，可以对桥梁结构进行力学上的简化。

1 建立简化多点碰撞模型

1.1 桥梁简化模型

目前，在进行桥梁性能研究时，通常将伸缩缝两侧结构视为独立结构分别展开研究，而梁体与桥台之间及梁体之间的伸缩缝就简化为碰撞接触单元，图1为常见桥梁形式。基于以上思路，在研究桥梁多点碰撞响应时将桥梁结构进行简化，并在有限元软件中创建碰撞模型进行结构多点碰撞的影响参数分析。计算结果不仅可以为桥梁多点碰撞研究提供参考，还可以为桥梁简化模型多点碰撞振动台试验进行探索。

图1 常见桥梁形式

桥梁简化模型的有限元模型如图2所示，3个边长150 mm的碰撞块均采用混凝土材料，两侧碰撞块由边长50 mm、高920 mm的方钢管托举，中间碰撞块由两块宽50 mm、厚3 mm、高920 mm的钢板托举。

图2 简化碰撞模型

1.2 碰撞接触单元

目前，接触单元法常见的几种接触单元模型中，线弹簧-阻尼模型（Kelvin模型）的碰撞模拟效果较好，并且容易在有限元软件中实现，因此得到了广泛的应用［6-8］。

Kelvin模型将桥梁伸缩缝简化为线性弹簧单元并联了一个线性阻尼单元，通过弹簧刚度来反应梁体碰撞刚度，通过弹簧的压缩来计算碰撞力，梁体在碰撞过程产生的能量损失则由线性阻尼器表达。Kelvin模型的力—位移关系如图3所示，其理论模型如图4所示。

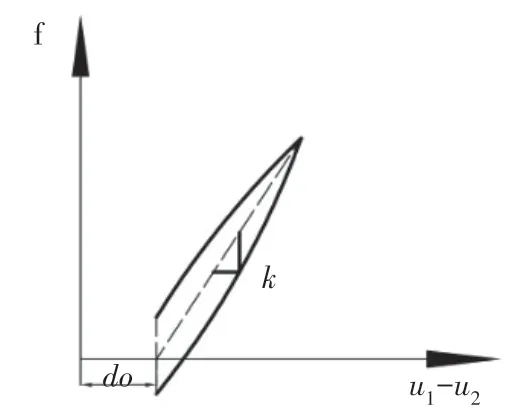
图3 Kelvin模型的力—位移关系

图4 Kelvin单元理论碰撞模型

Kelvin模型的碰撞力公式如式（1）。

式中：u1-u2-d0≥0，当u1-u2-d0＜0时，也就是梁体相对位移没达到伸缩缝距离时，未发生碰撞，碰撞力为0。本研究计算时采用Kelvin接触单元模型计算。

2 结构多点碰撞影响参数分析

2.1 碰撞刚度影响

为了研究碰撞刚度对碰撞响应的影响，本研究选取多个碰撞刚度进行计算分析，使用EL-Centro地震波，加速度峰值调整为0.45 g，工况布置如表1所示。

表1 不同碰撞刚度工况

图5给出了两侧间隙最大碰撞力随碰撞刚度变化的曲线图；图6给出了不同工况下的相邻碰撞块相对位移最小值在不同碰撞刚度下的变化曲线。从这些计算结果可以看出，当碰撞刚度增大时，会使间隙两侧碰撞块的相对位移减小，并不断趋近于初始碰撞间隙，但随着碰撞刚度继续增大，这种趋势会逐渐变得平缓，但碰撞块的相对位移总会超出初始碰撞间隙，超出的位移值实际上就是碰撞处节点互相侵入的距离。

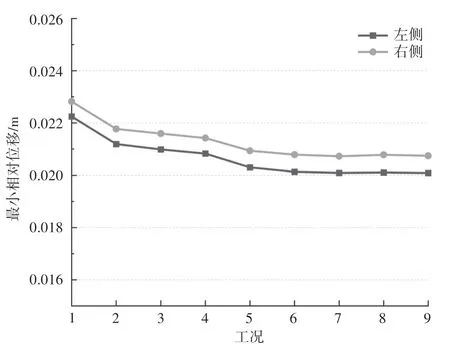
图6 左、右间隙碰撞块最小相对位移

由图5可知，碰撞力只在一定范围内随碰撞刚度增大而增大，当碰撞刚度继续增大后，由于碰撞块相对位移的减小，其碰撞力不但没有增加，反而减小了，继续增大碰撞刚度，最大碰撞力的变化曲线出现了离散现象，变化规律变得紊乱，右侧间隙处甚至出现了不合理的大碰撞力值。并且在实际计算中，当刚度过大时，也容易使计算不收敛。因此，合理的碰撞刚度取值对桥梁结构碰撞计算十分重要。

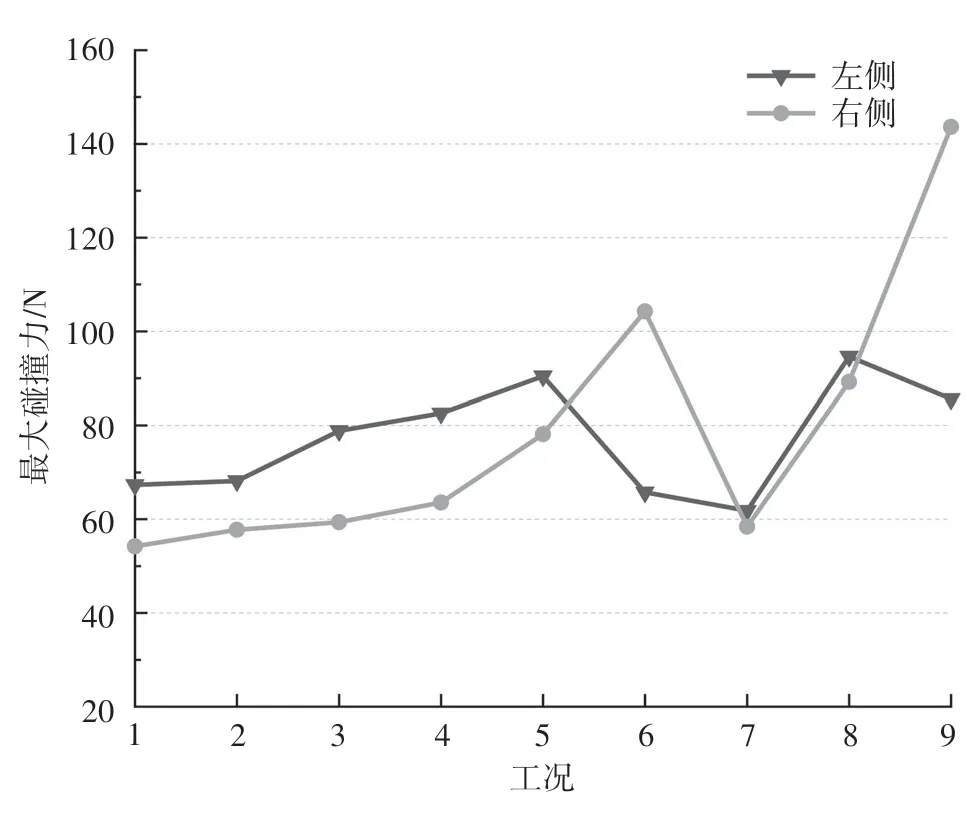
图5 不同碰撞刚度工况峰值碰撞力变化曲线

2.2 碰撞间隙的影响

初始碰撞间隙是结构碰撞的一个重要影响因素，本节将从17~32 mm之间取6个间隙值作为碰撞工况，采用EL-Centro地震波、Taft地震波、Northridge地震波进行计算分析，地震波峰值加速度统一调整为0.6 g，碰撞刚度取2×105N/m。

图7、图8是两侧间隙的碰撞次数随初始间隙变化的曲线；图9、图10为最大碰撞力随间隙改变而变化的曲线。从图中可以看到，初始间隙对结构碰撞响应的影响十分显著，但是初始间隙值的改变对结构碰撞力变化规律的影响却并不十分明显，这可能是两侧碰撞点之间相互影响的结果。此外，在初始间隙相同的情况下，不同地震波作用下的最大碰撞力相差较大。由此可见，与无约束结构单点碰撞不同，引入桥台限制作用并考虑多点碰撞时，初始间隙对结构的最大碰撞力的影响没有统一的规律，碰撞点之间存在相互影响，并且地震波种类的差异对结构多点碰撞最大碰撞力的变化规律也有明显的影响。

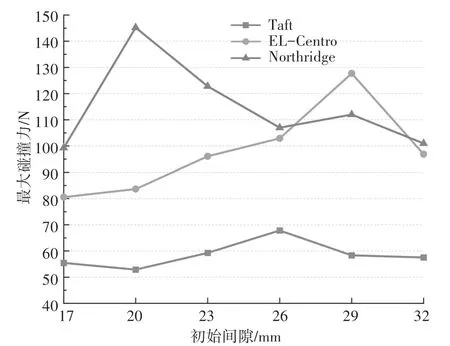
图9 不同地震波作用下各工况左侧间隙最大碰撞力

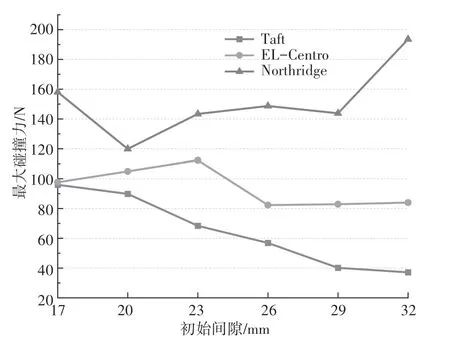
图10 不同地震波作用下各工况右侧间隙最大碰撞力

由图7、图8可以发现3条地震波激励下各不同碰撞间隙工况下两侧间隙的碰撞次数都呈现较明显的规律，即随初始间隙增大而减少。但是在同一初始间隙工况下，不同地震波作用下，模型左右间隙发生的碰撞次数也有明显差异，说明对于结构碰撞响应而言，地震波种类也是一个重要影响因素。

图7 不同地震波作用下各工况左侧间隙碰撞次数

图8 不同地震波作用下各工况右侧间隙碰撞次数

图11为墩底剪力随初始间隙变化的曲线。由图11可以看出，初始间隙对墩底剪力有明显的影响，在不同工况下墩底最大剪力变化呈现明显的规律，即随初始间隙增大而增大，且变化规律较为均匀，可见初始间隙是墩底冲剪受力变化的重要影响因素。

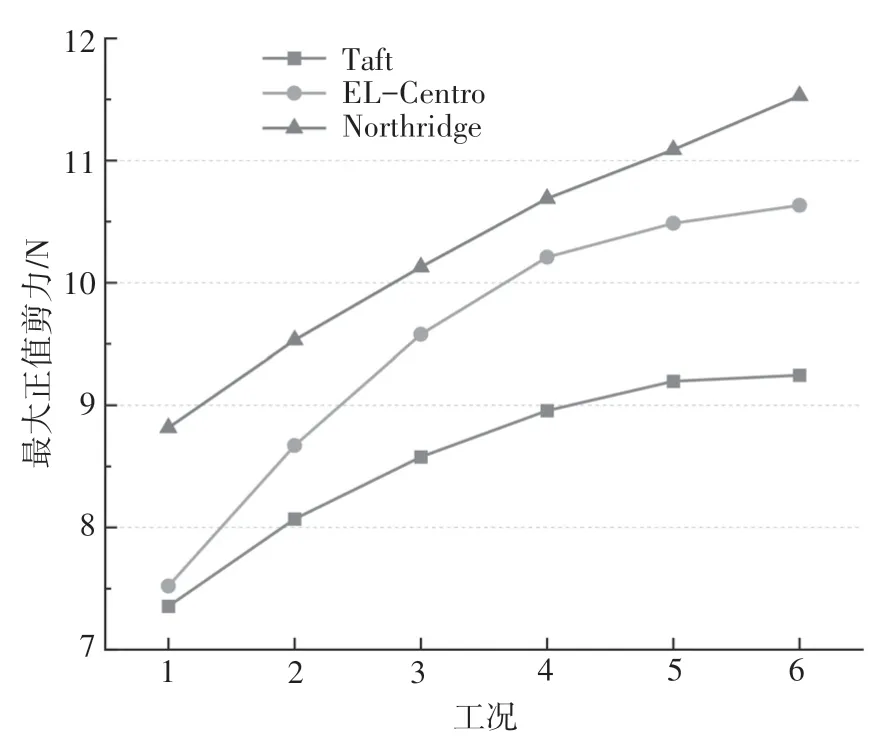
图11 不同地震波作用下各工况墩底最大剪力曲线

2.3 桥墩高度的影响

现有研究表明，桥墩高度变化对桥梁伸缩缝处的碰撞力有着显著的影响。为了探究结构高度变化对结构多点碰撞响应的影响。以初始高度0.92 m为第一个工况，共设置6个工况，后续每个工况墩柱依次增加0.1 m。

图12、图13给出了两侧间隙最大碰撞力随墩柱高度改变的变化曲线。从图中可以看出，在结构多点碰撞中，随着墩柱高度的增加，结构最大碰撞力的增长没有准确的规律性，其变化曲线起伏不定，但从总体上看，仍具备随墩柱高度增加而增大的这一趋势。在结构多点碰撞中，碰撞点之间存在相互影响，两侧刚度较大的碰撞块对中间碰撞块的位移有约束作用；另外，中间墩柱高度改变，而两侧墩柱的高度没有变化，相邻墩高比的变化也使得相邻结构的周期比改变，这些因素在一定程度上使碰撞模型的动力响应在地震荷载作用过程中有较大的改变，从而导致碰撞响应出现变化。这也是其碰撞力随结构墩柱高度改变的变化规律与单点碰撞有所出入的主要原因。

图13 不同墩柱高工况下右侧间隙最大碰撞力

图14 给出了各地震波在不同墩柱高工况下的墩底最大剪力。由图14可知，在结构多点碰撞中，结构墩柱高度对墩底内力有着显著的影响。随着结构墩柱高度逐渐增大，其刚度随之减小，墩柱底端剪力会逐渐减小，但这种趋势不会一直持续，当墩柱高度过大时，墩底剪力的变化速率会趋于平缓，直至不变。由此可见，在实际工程中，虽然较矮的桥墩可以有效地控制墩顶位移，但是会明显加大墩底的冲剪作用，当桥墩较矮时，应视实际情况对墩底予以加固。

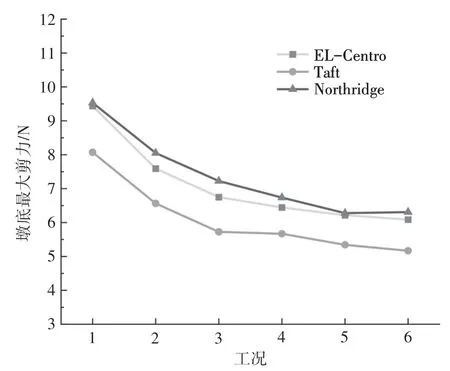
图14 不同墩柱高工况下墩底最大剪力

3 结论

本研究将常见桥梁形式按照力学规律进行了简化，形成了碰撞块的简化碰撞模型，通过有限元软件开展数值模拟仿真分析，对桥梁结构多点碰撞影响参数展开研究分析，得到以下结论。

①在结构多点碰撞中，碰撞刚度、碰撞间隙、桥墩高度都对碰撞响应有明显影响，但与影响规律与单点碰撞有较大的差异。

②桥墩高越高，相邻梁体间的碰撞力越大，但是墩底剪力变化趋势却与之相反。当桥墩高度降低，会使其刚度增大，进而放大地震作用下受到的冲剪作用。

③在结构多点碰撞中，除了上述影响因素外，地震波种类也是一个重要影响因素，不仅对结构最大碰撞力、碰撞次数有明显的影响，还在一定程度上影响桥墩受到的冲剪作用。