圆盘滚动的动力学分析
2023-03-13王盼李文博
王盼,李文博
圆盘滚动的动力学分析
王盼1,李文博2
(沈阳航空航天大学 1. 航空发动机学院,2. 理学院,辽宁 沈阳 110136)

圆盘;动力学;纯滚动;平面运动微分方程
圆盘的转动问题在日常生活中随处可见,如汽车车轮的滚动、齿轮的转动、圆柱形水杯的滚动等.圆盘按质量是否均匀分布可分为均质圆盘和偏心圆盘2类.万邦良[1]等对均质圆盘在平面纯滚动这一现象做了较为详细的理论分析,分析了此类圆盘在平面纯滚动的充分必要条件.偏心圆盘较均质圆盘滚动有更加有趣的现象,在第七届周培源大学生力学竞赛试题中,就有一道关于水平面偏心轮跳滚现象的解释题[2];在第十一届周培源大学生力学竞赛团体赛中,有关偏心轮在斜面跳滚现象的题再次出现[3].本文对圆盘在水平面和斜面上的滚动现象进行了较详细的动力学分析.
1 均质圆盘
1.1 均质圆盘平面滚动
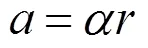
在圆盘上施加一水平力后,圆盘继续做纯滚动,摩擦力的方向可能会发生变化.以质心为坐标原点,建立坐标系(见图2).
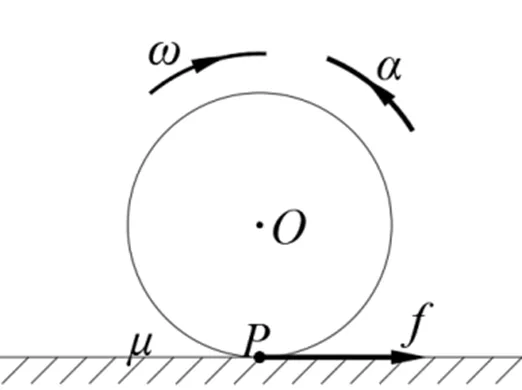
图1 圆盘平面滚动
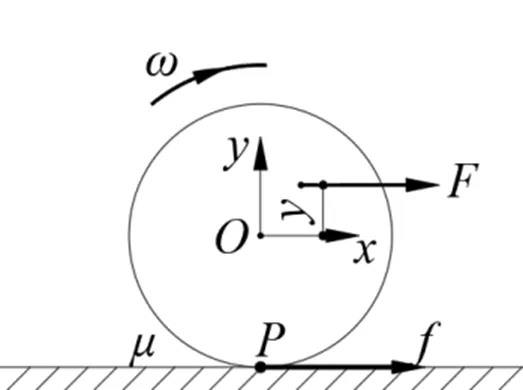
图2 圆盘受外力后滚动


1.2 均质圆盘斜面滚动
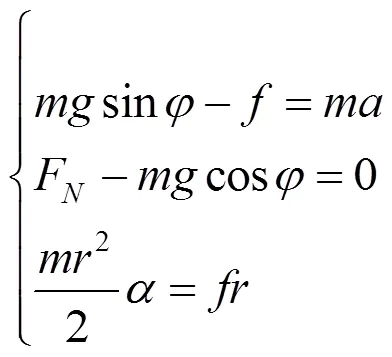

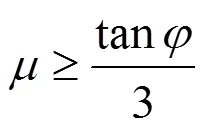
式(5)是斜面上未施加外力时圆盘做纯滚动的必要条件.考虑施加一沿斜面向上的外力后(见图4),与圆盘水平面施加外力分析相似,这里也是在质心处建立坐标系,轴方向沿斜面方向.
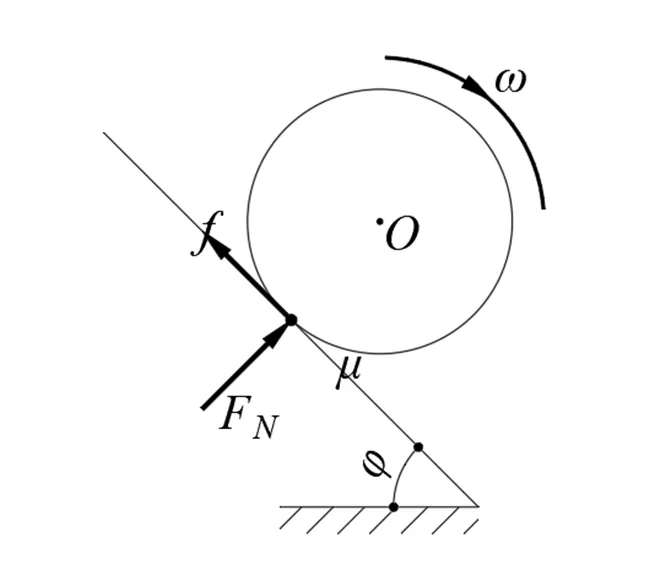
图3 圆盘斜面滚动

图4 圆盘受外力后滚动(斜面)

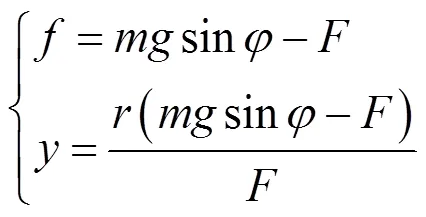
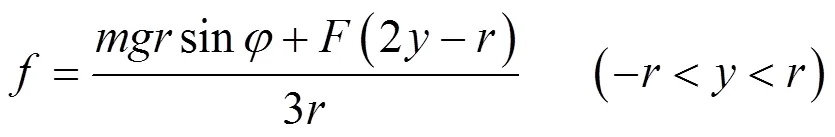
2 偏心圆盘
在上述分析中,所针对的圆盘均为均质圆盘,但在生活中,很难保证圆盘质量均匀分布.就非均质圆盘(偏心圆盘)在平面和斜面进行动力学分析.
2.1 偏心圆盘平面滚动
当偏心圆盘以一定角速度在粗糙水平面滚动时,与均质圆盘基本相似,但质心加速度略有不同.以圆心为基点,质心的加速度为
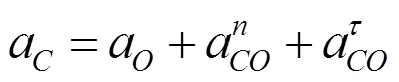


图5 偏心圆盘平面滚动

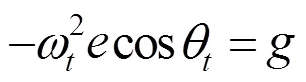
由于水平面存在摩擦,圆盘在水平面滚动时,角速度逐渐减小,最终使得圆盘在水平面滚动而不会跳起,出现偏心圆盘往回滚的现象.
2.2 偏心圆盘斜面滚动
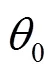
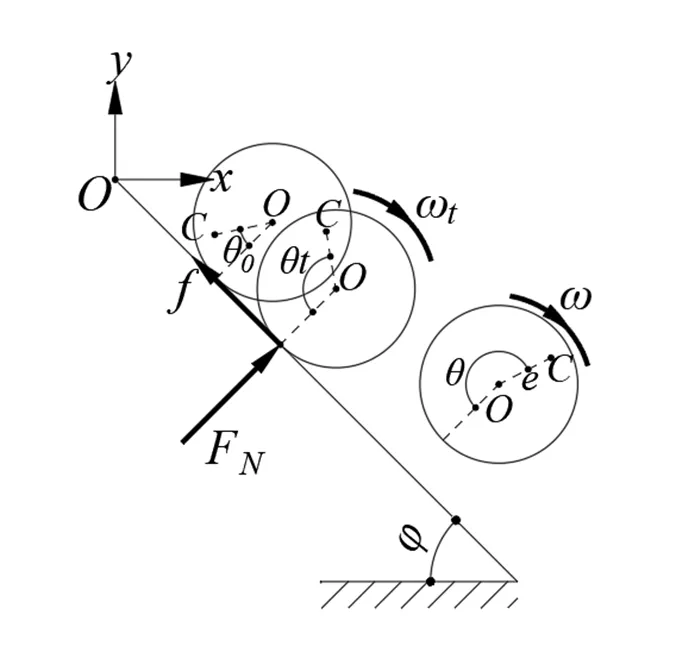
图6 偏心圆盘斜面滚动
偏心圆盘在斜面上的运动与在水平面运动一样,也会出现跳滚现象[5],偏心圆盘在斜面跳起的条件为


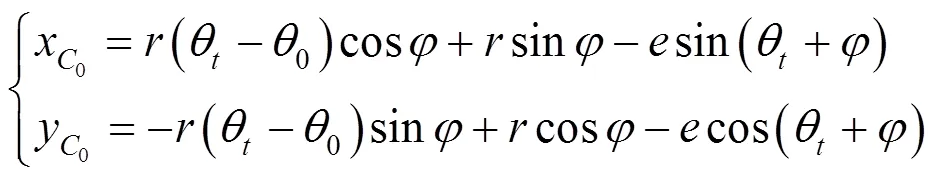
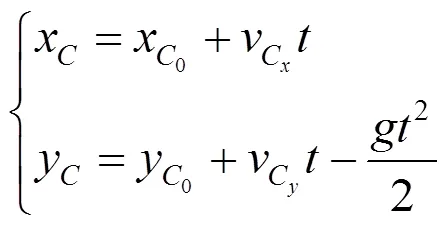
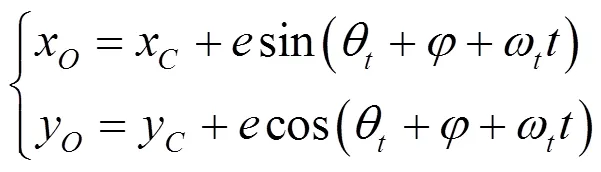
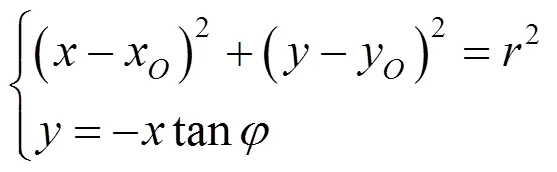
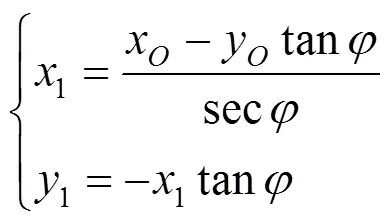
偏心圆盘离开斜面后,竖直方向速度变化与水平面起跳后竖直速度方向变化一样,也是先做加速上升运动,再做减速上升运动,最后做加速下降运动.偏心圆盘与斜面碰撞后,速度会发生变化,这里不再做具体分析.
3 结语
本文对均质和偏心2种圆盘在水平面及斜面的滚动进行了动力学分析.均质圆盘在水平面和斜面做纯滚动时,摩擦力不做功.在均质圆盘上作用外力时,外力的大小以及作用线位置不同,摩擦力的方向会发生变化.偏心圆盘在水平面和斜面滚动时会出现跳滚现象,偏心圆盘发生跳滚的角速度临界条件为,只与偏心距和接触面倾斜角度有关.当偏心圆盘离开接触面时,先做加速上升运动,再做减速上升运动,最后做加速下降运动.偏心圆盘在水平面做跳滚运动,由于有摩擦阻力,圆盘的角速度减小到临界角速度后,不会再跳起,甚至在水平面还会往回滚动.计算了偏心圆盘离开斜面后圆心运动方程和第一次与斜面的碰撞点坐标.
[1] 万邦良,邱支振.均质圆盘平面运动的动力学分析[J].华东冶金学院学报,1989(4):82-85,81.
[2] 西北工业大学.第七届全国周培源大学生力学竞赛试题[J].力学与实践,2009,31(4):103-105.
[3] 任毅如,方棋洪,肖万伸,等.第十一届全国周培源大学生力学竞赛“理论设计与操作”团体赛命题和竞赛总结[J].力学与实践,2018,40(5):599-608.
[4] 陈小亮.圆环跳滚现象的力学分析[J].力学与实践,2010,32(6):120-121.
[5] 彭凡,刘文洋,方棋洪,等.偏心圆轮沿斜面纯滚动至连续弹跳的动力学分析[J].力学与实践,2019,41(1):72-75.
Dynamic analysis of disc rolling
WANG Pan1,LI Wenbo2
(1. School of Aero Engine,2. School of Science,Shenyang Aerospace University,Shenyang 110136,China)
disc;dynamics;pure rolling;differential equation of plane motion
1007-9831(2023)01-0042-05
O313.3
A
10.3969/j.issn.1007-9831.2023.01.009
2022-07-08
沈阳航空航天大学创新创业训练计划项目(X202110143029)
王盼(2001-),男,湖南娄底人,在读本科生.E-mail:wangpan0244@163.com
李文博(1986-),女,黑龙江牡丹江人,讲师,博士,从事应用物理研究.E-mail:20180047@sau.edu.cn
