一般方程表示下曲面上曲线测地曲率的计算公式及其应用

梁钊，张量

一般方程表示下曲面上曲线测地曲率的计算公式及其应用

梁钊，张量

（安徽师范大学 数学与统计学院，安徽 芜湖 241002）

测地曲率是经典微分几何曲面理论中一个重要的内蕴几何量，测地曲率恒为零的曲线即曲面上的测地线．给出了一般方程表示下曲面上曲线测地曲率的计算公式，利用该计算公式给出了椭球面上圆截线问题的一种微分几何解决方法.

测地曲率；椭球面；圆截线

1　引言及预备知识

测地曲率可以用来反映曲面上曲线的局部弯曲情况，其本质只与曲面的第一基本形式有关，是经典微分几何曲面理论中一个重要的内蕴几何量．目前关于测地曲率的计算方法多数都是在曲线的参数表示下给出的[1-7]．本文给出一般方程表示下曲面上曲线测地曲率的计算公式，并利用该计算公式给出解析几何中椭球面上圆截线问题的一种微分几何解决方法．

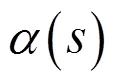
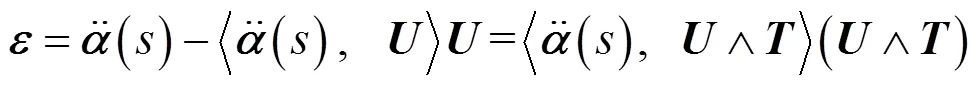
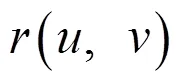
2　主要结果及证明

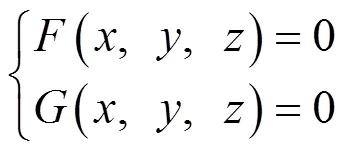
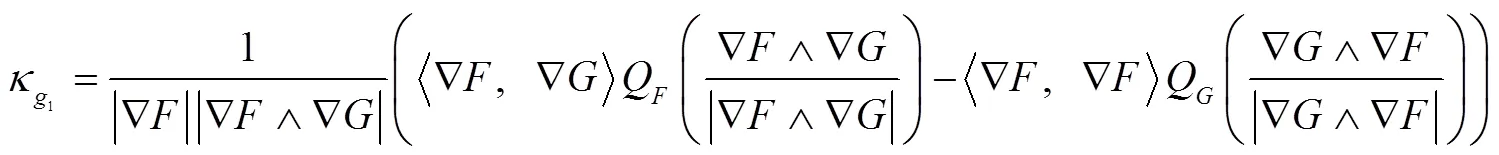
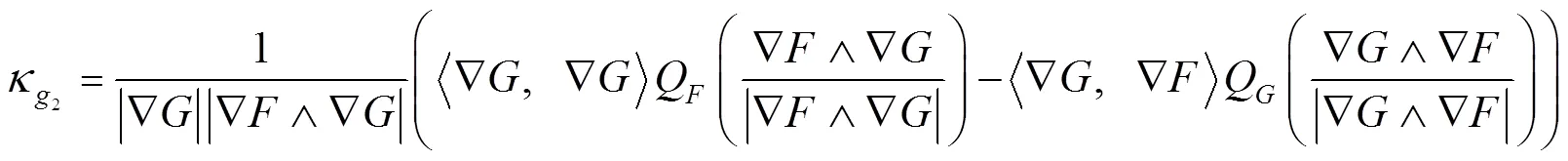
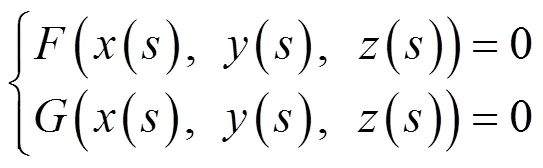
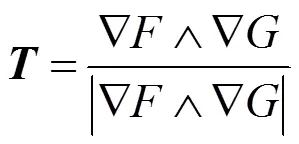
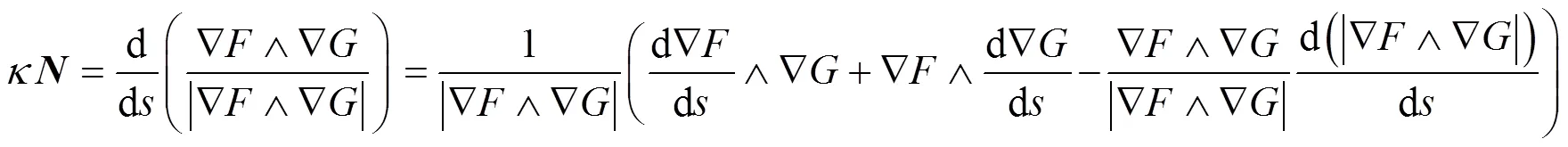
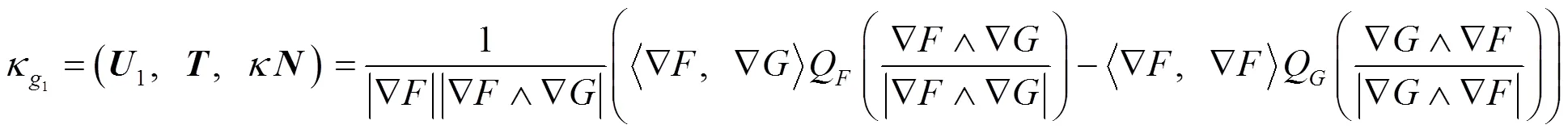
证毕．

椭球面的圆截线问题是解析几何中的一个经典问题[8-9]，文献[10]通过将椭球面与平面交线参数化给出了椭球面圆截线问题的一种微分几何解决方法．利用定理1，可得到不通过参数化给出椭球面圆截线问题的另一种微分几何解决方法．

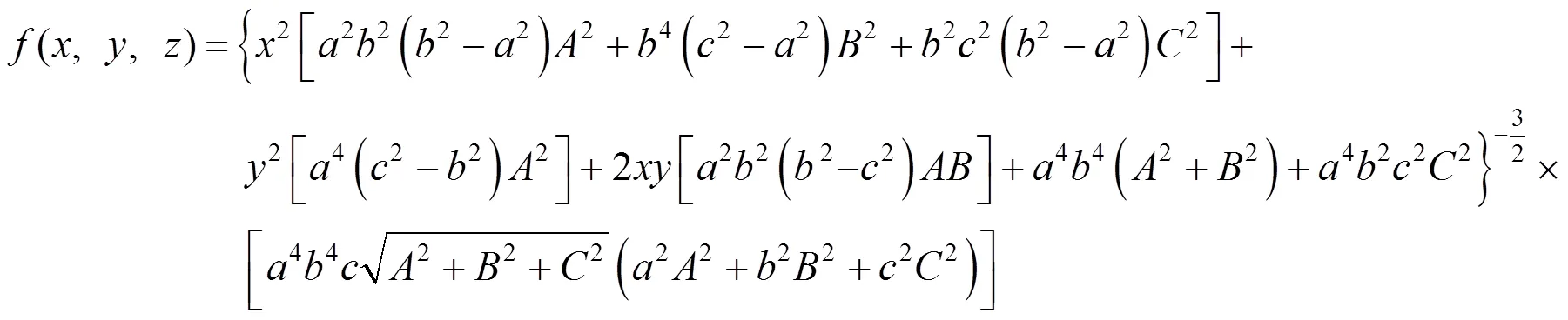
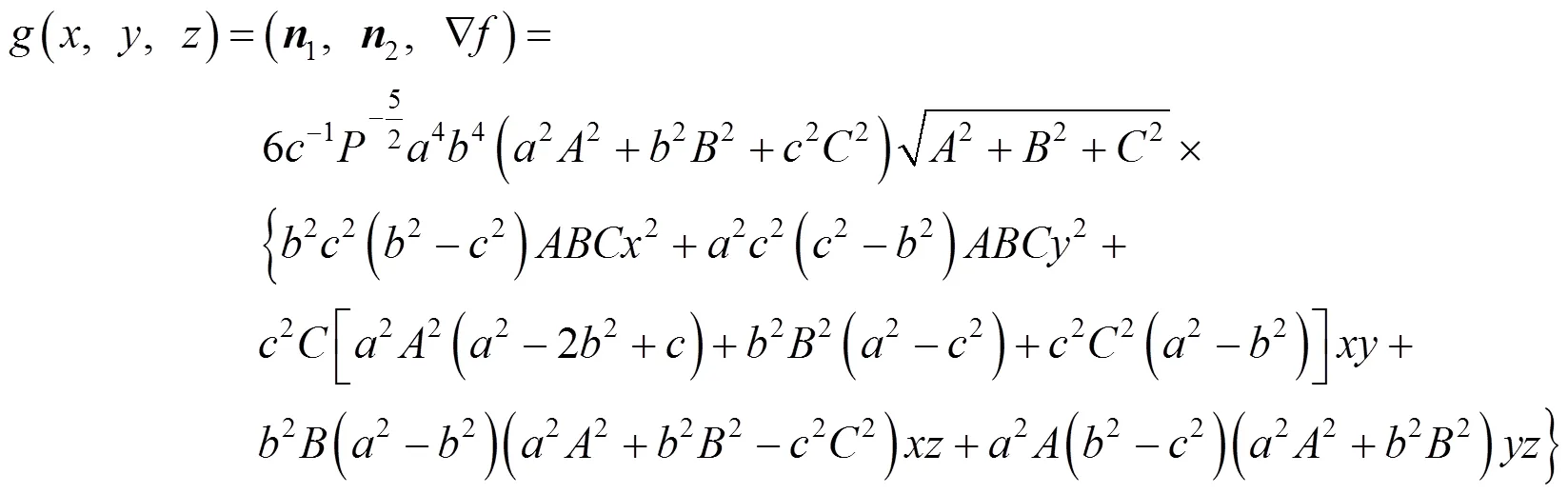
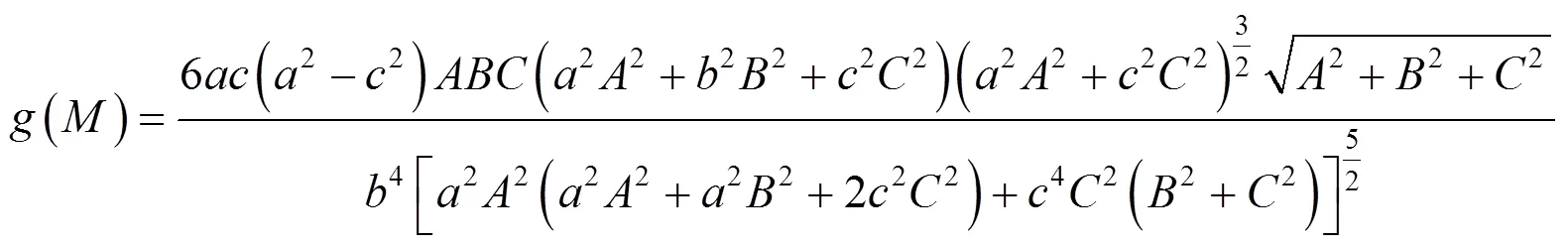
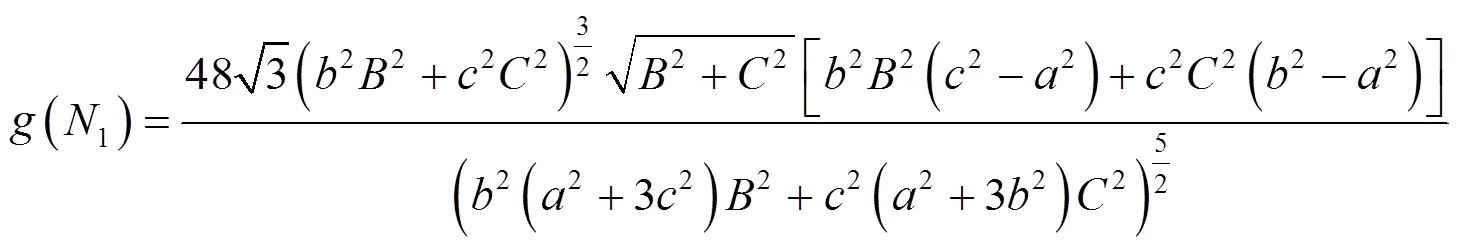
[1] Manfredo P，Carmod O．Differential Geometry of Curves and Surfaces[M]．Upper Saddle River：Prentice-Hall，1976：15-185．

[2] John O．Differential Geometry and Its Applications，Second Edition[M]．Cleveland：Cleveland State University Press，2004：17，154-195．

[3] 邢家省，张光照．曲面上曲线的测地曲率向量的注记[J]．吉首大学学报（自然科学版），2013，34（4）：8-10．

[4] 邢家省，白璐，罗秀华．测地曲率计算公式的推导方法[J]．吉首大学学报（自然科学版），2015，36（5）：8-11．

[5] 罗秀华，张光照，邢家省．曲面正交网下测地曲率和高斯曲率的计算公式的推导方法[J]．河南科学，2015，33（7）：1082-1086．

[6] 邢家省，高建全，罗秀华．曲面上测地线和短程线的性质[J]．四川理工学院学报（自然科学版），2015，28（1）：64-66．

[7] 黄瑞．几类特殊曲面曲线的法曲率测地曲率和测地挠率的计算[J]．阜阳师范学院学报（自然科学版），2017，34（3）：24-26．

[8] 房亮．关于椭球面的平截线的探讨[J]．泰安师专学报，2001（2）：23-26．

[9] 房亮．几种常见二次曲面的圆截线[J]．泰山学院学报，2004（6）：33-35．

[10] 姜旭，张量．椭球面圆截线问题的微分几何解法[J]．高等数学研究，2016，19（1）：75-77．

Calculation formula of the geodesic curvature of a curve on a surface represented by the general equation and its applications

LIANG Zhao，ZHANG Liang

（School of Mathematics and Statistics，Anhui Normal University，Wuhu 241002，China）

Geodesic curvature is an important intrinsic geometric quantity in the theory of surfaces in classical differential geometry，and it is known that a curve with constant zero geodesic curvature is a geodesic on a surface．A formula of the geodesic curvature of a curve on a surface represented by the general equation was given，and it was used to give a differential geometric solution to the circular transection problem on an ellipsoid.

geodesic curvature；ellipsoid；circular transection.

1007-9831（2023）01-0010-05

O186.11

A

10.3969/j.issn.1007-9831.2023.01.003

2022-05-10

梁钊（2000-），男，安徽淮北人，在读本科生．E-mail：2680990056@qq.com

张量（1979-），男，安徽芜湖人，副教授，从事几何学研究．E-mail：zhliang43@163.com