考虑伤情随机恶化的政企应急物资采购决策研究

王建华，赵俊明（江南大学 商学院，江苏 无锡 214122）

0 引言

各类灾害事故给我国经济民生造成损害的同时，也同样造成了人员伤亡。但是灾害自身的特性——突发性、不确定性也决定了对于应急物资的需求的不确定性，因此仅靠政府救灾存在不少的弊端。一是对于应急物资的储备难以满足应急的需要；二是政府自身采取行动不如发动全社会的资源来的有效。

针对于此，卢少平等人[1]提出社会化的应急物资储备，使供应商在救灾中充分发挥物资供给效用，为当前应急物资储备方式提供有效补充。田军等人[2-4]分别运用数量柔性契约、看跌期权契约、生产能力期权契约三种契约方式进行研究应急物资采购供应链中政企的最优采购决策。Zhongquan Hu 等人[5]更进一步利用看跌期权契约，构建出政企共同应急物资模型，并得出政企双赢的条件和协调应急物资供应链。但同时上述文献是基于突发灾害初始状态后不再转移，与现实条件不完全相符的前提，因此刘阳等人[6]将突发灾害转移视为有限齐次的Markov 链，构建应急物资采购定价模型进行分析，并得出既可以提高应急物资储备水平，又可以保障供应商的合理收益及控制政府成本的政企双赢。

应急物资的采购及使用其最终作用对象都是人，因此，人的伤情状态直接影响到应急物资的需求量。有学者从针对伤员伤情进行资源分配[7]、患者伤情对于医院的选择[8]、伤情的随机恶化[9]以及综合考虑路况和伤员数量等的影响[10]，对于灾民的伤情状态应急物资的调配应进行细化研究。

上述的国内外学者研究既分析了政企合作达成时条件以及在其中最优决策问题，又对于伤员伤情演变的影响进行了有效分析，并且取得了一定成果，但是上述文献中，对于伤员伤情的研究更多集中在应急物流调度方面，在应急物资采购方面的研究影响较少。因此，本文在考虑数量柔性契约的政企应急物资采购供应链中，引入伤情状态随机变化，对灾民伤情的转移情形概率对于政企决策的影响进行研究。

1 问题描述

1.1 问题和决策

突发事件后，出现伤情的灾民不同状态出现的应急物资需求不同，所造成的政企储备和采购决策也影响不同，在此基础考虑现实在突发事件采购中，政府补贴政策的影响，构建基于数量柔性契约的政企应急物资采购模型进行分析。作为决策中主导的政府，在突发事件发生前，向协议企业按照初始应急物资单位价格进行常规的应急物资储备采购；协议企业接受该契约，为政府提供常规应急物资数量订单的物资并制定相应的柔性物资生产与储备数量。在突发事件发生时，按照契约，政府根据灾民对应急物资的需求量，以契约中制定的柔性价格采购一定数量的应急物资。

1.2 参数符号

参数如下：

x：灾民对应急物资的需求量，最大值为U，密度函数f（x），分布函数F（x），F（x）∈(0,1]。P0：未发生突发事件前的初始应急物资单位价格，P0＞0。Q0：政府常备的应急物资储备量。C：协议企业应急物资单位成本，C=C1+C2，其中：C1为协议企业应急物资的单位生产成本，C2为应急物资的单位储存成本。δ：单位应急物资残值，P0＞δ。ω1：政府对应急物资需求在(Q0,Q0+Q1]区间内时，应急物资的单位补贴系数。m：政府协商和购买应急物资缺口所耗费的单位成本，m＞P0。Li：表示灾民不同的受伤状态，i=1,2,3，其意义分别为中伤，重伤和死亡。n 步转移概率，表示灾害初始状态为Li的概率，发生突发事件的应急物资单位价格，P1＞P0。Q1：协议企业的生产与储备的应急物资数量。ρ：突发事件发生的概率。ω2：政府对应急物资需求在(Q0+Q1,U]区间内时，应急物资的单位补贴系数，P0＞ω2＞ω1。

1.3 相关参数关系

m＞P0＞ω2＞ω1＞＞δ：政府购买所需不足物资耗费的成本大于应急物资的单位价格，其中单位应急物资的残值远远小于单位补贴、单位价格和耗费成本。

1.4 基本假设

（1）政府采购物资救援一个受灾点，受灾点有多个灾民，有一个物资供应协议企业，且有一个现货市场，政府不得强制性征用物资，采购定价模型发挥市场机制下的价格效果；（2）考虑不同灾民会出现不同伤情状态，产生不同应急物资需求，为方便计算，将灾民伤情状态看做统一整体进行计算；（3）灾民病情状态L1和L2互通，L1可达L3，L2可达L3，但L3不可到达L2或L1，其转移概率P31=P32=0（特殊的P33=1），此假设表明灾民L3状态时，不可状态转移，符合现实情况；（4）在政府储备或者政府可以从协议企业及时购买到物资储备时，L3状态不可发生，只有超出Q0+Q1时才可能发生伤员L3状态；（5）政企关系中，政府为主导地位，协议企业为从属地位，政府与协议企业是完全理性和风险中性的，且信息完全对称；（6）灾民的伤情状态转移具有平稳性，且状态转移步数是有限次的，最多允许二步状态转移；（7）突发事件的持续时间远小于政府救援时间，不考虑突发事件持续时间的影响。

1.5 伤情状态转移的Markov 过程分析

本文设为一个有限次Markov 链研究伤情状态转移过程，并基于伤员状态将其划分为L1、L2和L3三种状态。用P｛Xtn+1=Lj|Xtn=Li｝表示从处在tn时刻时伤情状态Li转移到处在tn+1时刻时伤情状态Lj的条件概率。

考虑到突发事件是ρ 概率发生的，并根据应急物资储备、伤员初始伤情状态以及状态转移的变化，推理出以下的情形：

（1）0＜x≤Q0时，即t0时刻，伤员的初始伤情状态随机。在突发事件发生后，即t1时刻，政府立刻调配政府储备应急物资进行救援，伤情状态一步转移路径集合为｛L1-L1,L2-L1｝，公式表示为P ｛Xt1=Lj|Xt0=Li｝，即

（2）Q0＜x≤Q0+Q1时，根据上一阶段的状态转移结果，在t2时刻做出相应的应急物资决策。伤情状态二步转移路径集合为｛L1-L1-L1,L1-L1-L2,L1-L2-L1,L1-L2-L2,L2-L1-L1,L2-L1-L2,L2-L2-L1,L2-L2-L2｝，公式表示为。例如，初始状态为L1，经过政府的救援，t1时伤情状态变为L2，政府需要加大对于应急物资的采购。t2时刻的决策实质上依赖政府储备物资满不满足灾民伤情的需要。

（3）Q0+Q1＜x≤U 时，经过t2时刻，政府从协议企业采购应急物资后，伤情状态再次发生转移，说明物资储备难以满足需求，转移至L3状态，伤情状态二步转移路径集合为｛L1-L1-L3,L1-L2-L3,L1-L3-L3,L2-L1-L3,L2-L2-L3,L2-L3-L3,L3-L3-L3｝，公式表示为P ｛Xt2=Lj|Xt0=Li｝，即

2 建立模型

2.1 考虑伤情随机变化的协议企业决策

针对于假设，构建协议企业利润函数式为：

公式（1）：第一、二项为协议企业固定获得政府Q0订单所带来的收益；第三项为未发生突发事件时协议企业的利润；第四项为未发生突发事件时(0,Q0]，(Q0,Q0+Q1]和(Q0+Q1,U]情形下协议企业的收益。

（P1-δ+ω1-C时，公式（3）为负值，则公式（1）是关于Q1的凹函数，存在着使协议企业利润获得最大值的最优物资量。通过对于公式（2）取零，可得最优生产与储备的物资量如下：

存在协议企业所允许的政府制定的单位最低物资价格，使得协议企业达到盈利而政府最低成本的条件。

由于函数的复杂性，因此本文以伤情状态随机恶化为例。引用龚英等人[10]论文中情形1 的伤情变化矩阵，如下所示：

将以上公式代入公式（4）和公式（5），化简可得：

2.2 考虑伤情随机变化的政府决策

政府作为Stackelberg 博弈中的主导者，在考虑到协议企业对于政府的决策所能做出的反应后，根据突发事件的发生概率应急物资的成本等因素为参考，为做出以最优化成本和激励协议企业的物资生产储备为目的最优的决策，整理出以下成本函数：

公式（10）：第一项为政府Q0的采购和储备成本；第二项为突发事件未发生时的政府Q0残值收益；第三项为突发事件发生后的采购、补贴等成本，包括(0,Q0]，(Q0,Q0+Q1]和(Q0+Q1,U]三种情形不同转移路径所产生的成本。

2.3 数量柔性契约与分散决策对比

分散决策政企非合作条件下，只存在政府常规应急物资储备，极大限制了政府的救灾能力，无法保证应急物资的充足可用。同时，协议企业不存在应急物资的储备，根据政府的订单生产应急物资[11]，因此协议企业的利润函数：

应急物资需求不同，政府会产生不同的成本情形，参考数量柔性契约下成本函数，分散非合作决策下的政府成本函数为：

为了方便计算，设Q0为分散非合作下政府最大的应急物资储备。同时，得出合作机制和分散非合作的优劣，对两者的政府和企业利润和成本进行比较，ΔfG=fGd-fG,ΔfE=fEd-fE。

数量柔性契约机制与分散非合作下的政府成本之差为：

数量柔性契约机制与分散非合作条件下的协议企业利润差值公式：

当满足公式（19）时，协议企业在契约合作中的利润会得到进一步提高。

综述可得契约合作下协议企业利润，政府成本得到改善以及政企达成合作的条件：

3 仿真实验

3.1 案例描述与计算

政府与一个协议企业签订契约对应急物资进行储备合作。由于缺乏标准的相关算例，考虑到文献[10]的相似性，以其中的数据作为基础展开研究，相关参数如下：ρ=0.3、C1=40、C2=0.8、P0=45、δ=5、m=460、Q0=10 000、U=20 000、ω1=30、ω2=40，一步转移概率矩阵

借用MATLAB2014a，计算结果：协议企业能够接受的最低价格为614.54 元/件，政府最优的采购价格为1 792.45 元/件；协议企业的生产与储备应急物资量为1 960.47 件，基于以上的结果，政府最优成本为2 304 879.19 元，协议企业的最优利润为127 716.39 元。

3.2 敏感性分析

3.2.1 政府常规应急物资储备Q0的敏感性分析

政府Q0来自于对以往数据的总结，同时，储备受限于库存容量、购买成本以及突发事件中应急物资需求的不确定性和突发性等因素。因此，对于灾民所需的应急物资不可能次次满足。本节在政府Q0变化，而其他变量一定下，探究政府的采购策略影响，并分别对政府的成本和协议企业的利润进行敏感性分析，如表1 所示。

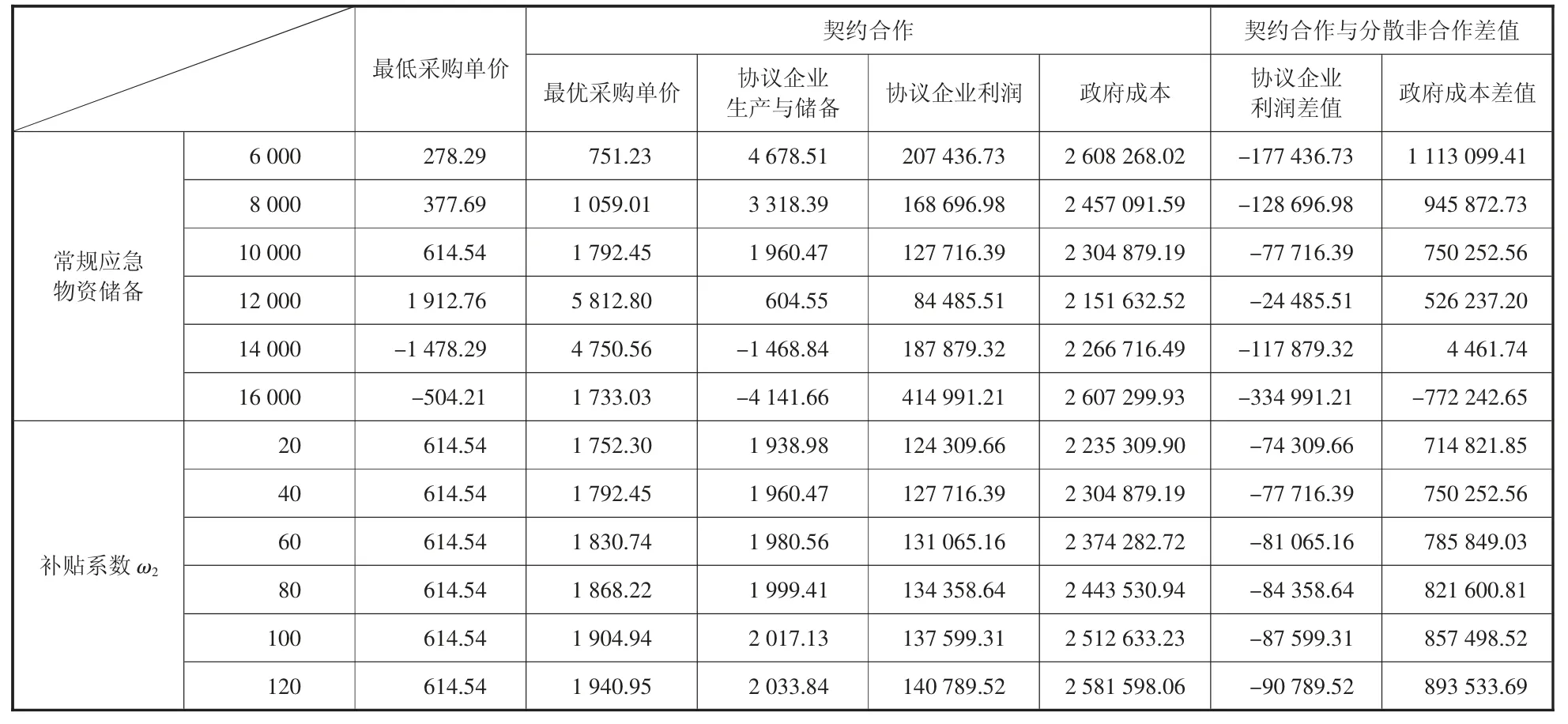
表1 敏感性分析数据表

（1）政府Q0与协议企业Q1成反比，Q0的增加使得协议企业出售应急物资的难度加大。当政府Q0处于较高水平即14 000以上而成本增加时，协议企业Q1远低于政府Q0，甚至负储备但是利润增加，表明政府的应急物资可满足灾民伤情的需要，协议企业的利润增加可能来自于应急物资价格增加。

（2）政府Q0增加变化的同时，协议企业利润差和政府成本差也出现降低的总趋势变化，这表明契约合作下协议企业利润减少和政府成本增加，政府合作的意向逐渐降低。政府Q0与协议企业Q1成反比，政府能满足伤者应急物资的需求，但是却没有保障协议企业相关利益。这表明保持适当水平常规应急物资对于保证协议企业利润和政府成本的重要性。

（3）政府Q0变化对于应急物资的采购单价产生重要影响。一方面，随着政府Q0增加，最优采购单价逐渐拉大与最低采购单价差距，表明协议企业的库存成本和物资残值的浪费等总和不断增加；另一方面，在任意固定政府Q0下，应急物资的最低或者最优采购单价都远超出突发事件前的采购单价，灾民个人无法承担伤情的治疗费用，需要政府出面支持治疗和强有力的调控市场应急物资的单价。

3.2.2 政府补贴系数ω2的敏感性分析

在应急物资需求超过政府Q0与协议企业Q1总量时，政府不仅需要承担相应的协商和购买单位物资缺货成本，还需承担为了补贴和激励市场协议企业提供应急物资进行单位物资的补贴成本，本节将对不同单位补贴系数下的政企决策策略进行敏感性分析，如表1 所示。

（1）单位补贴系数ω2的变化对于政府制定的最低采购单价没有影响。应急物资最低采购单价始终不变且始终低于最优采购单价，协议企业提供应急物资储备的意愿不强烈。数量柔性契约的机制，在一定程度上给予了协议企业自主权，且政府制定的最低采购单价，是保障协议企业的利润下限，提高提供应急物资积极性的重要方式。

（2）契约合作的协议企业利润和政府成本随着单位补贴系数ω2的增加而增加，表明伤者病情状态恶化加剧，需要大量的应急物资逐渐超出了政府的控制，政府通过提高最优的采购单价来激励协议企业提高应急物资生产与储备，但影响微小，有利于协议企业利润增加而不利于政府成本。因此在政企合作前提下，政府应该积极寻找其他有效激励的同时，拓宽应急物资的获取渠道。

4 结论

本文考虑灾民伤情状态转移对于应急物资采购定价决策的影响，构建了基于灾民伤情随机恶化转移的数量柔性契约采购定价模型，分析了灾民伤情随机恶化下政企达成契约合作的条件以及双方的最优决策。

研究结果表明，相较于分散非合作的条件，考虑数量柔性契约合作下的灾民伤情随机恶化的应急物资采购定价模型既可以有效地应对突发事件的冲击，提高模型的稳定性，又可以采取合理的定价保障协议企业的利润以及控制政府的成本，实现政企双赢的最优决策。同时，根据敏感性分析，政府追求成本与协议企业追求利润是矛盾点，在一定条件下，政府应该加强宏观调控稳定市场，首先保证应急物资储备充足和对于灾民伤情稳定，并给予一定的补贴保证协议企业的盈利下限；政府对于应急物资的采购应实现多渠道，避免单一供应商，控制成本并实现有效的应急物资救援；将伤情划分为三级，并对其不同的需求进行预测，更有利政府应急物资资源的有效利用。

本文将Markov 链与灾民伤情状态相结合，使得应急物资的采购更加具有现实意义，不仅提高了政府对于应急物资储备水平的成本控制和协议企业的利润改善，同时也使得应急物资采购决策更具有意义。但是，本文只分析了随机恶化状态下的一步与二步转移概率对于政府应急采购的影响，后续可以研究多步的转移概率对于应急物资采购的影响。