考虑有色噪声影响的脉冲星导航2级强跟踪差分滤波器

2023-03-12许强崔洪亮丁邦平赵爱罡赵阳

航空学报 2023年3期

许强，崔洪亮，丁邦平，赵爱罡，赵阳

青州高新技术研究所测试控制系，潍坊 262500

X射线脉冲星是一种能够周期性发射稳定X射线脉冲信号的中子星［1］。利用这一脉冲信号实现定位、授时功能的导航方法称为X射线脉冲星导航。它相比于传统的惯性导航、无线电导航和星光导航等导航方式具有累积误差较小、潜在应用情景广泛、信号不易受地面干扰源和天体运动影响、兼具授时功能等优点。目前已经有大量的国内外学者研究了其在近地卫星导航任务和地月轨道转移、火星探测等行星际探测任务中的应用问题［2-4］。

根据相关原理，X射线脉冲星导航需要使用到包括中心天体在内的众多太阳系天体的星历数据［5］。而以近地卫星为例，目前已发表的相关文献证明1 km的地球轨道误差就会对导航结果带来将近千米级的定位误差［6-7］。所以X射线脉冲星导航技术的应用对太阳系内天体的星历数据精度提出了较高要求。此外，目前绝大多数的研究文献均将导航滤波器模型中的过程噪声与观测噪声认为是高斯白噪声［8-11］。过程噪声主要为除中心天体外其他天体对航天器的摄动影响，而观测噪声为探测器对X射线光子的探测噪声。实际上，这2部分噪声在天体运动等各方面因素的影响下不仅很难保证为白噪声，而且两者间还可能存在相关的情况。如果采用基于白噪声假设的数据模型进行建模解算，那么同样会影响计算精度。

目前，太阳系内行星星历的计算主要依赖于甚长基线干涉测量技术（Very Long Baseline Interferometry， VLBI）技术和不同空间任务返回的观测数据，测定精度着实有限。以目前应用较为广泛的由美国喷气推进实验室发布的DE（De⁃velopment Ephemerides）星历为例，地球的位置精度只能精确到千米以内，木星更是仅能到几十千米［12-13］。因此，如何降低太阳系内星历误差对X射线脉冲星导航的影响已经成为一项亟待解决的实际问题。有学者研究了增广估计算法以排除星历误差的干扰［7］。但是该方法会导致系统的状态量维数增加，带来较重的运算负担和数值病态问题。而且，增广估计算法将太阳系内星历误差认为是不变的。考虑到实际星历误差会存在缓慢的变化，增广估计算法长时间运行时的跟踪性能无法保证。其他学者还研究了不同形式的差分导航算法［14-16］。但是这些导航算法大多没有考虑差分计算过程中会导致过程噪声与观测噪声相关的问题。虽然文献［14］考虑了该问题，但它与其他研究文献一样，对原始模型中的过程噪声和观测噪声都非常理想地认为是高斯白噪声。而文献［16］采用的方法是多航天器间观测数据的差分计算。该方法虽然具有一定效果，但并不适合单个航天器的导航系统。

本文针对以上问题提出了适合绕某一中心天体轨道运行的2级强跟踪差分卡尔曼滤波器（Two-stage Strong Tracking Differential Kal⁃man Filter，TSTDKF）。首先将变化较为缓慢的中心天体星历误差作为独立偏差滤波器的状态量予以实时估计。考虑到星历的周年变化，构建了多重自适应调节因子以保证算法的跟踪精度。为解决原始模型中可能存在的有色噪声问题，将第1级滤波器设计为一种改进的差分卡尔曼滤波器，提高其对有色噪声的鲁棒性能，拓宽X射线脉冲星的应用范围。

1 X射线脉冲星导航原理

以绕地球运行的航天器为例，X射线脉冲星导航的原理可描述为如图 1所示。其中，c为光速；rsat为卫星在国际天球参考坐标系（Interna⁃tional Celestial Reference System， ICRS）［17］中的位置矢量；rE和νE分别为地球在ICRS坐标系中的位置和速度矢量；r和ν分别为航天器在地球质心坐标系（Earth Centered Inertial， ECI）中的位置矢量和速度矢量，且满足rsat=rE+r；tSSB和tSC分别为太阳系质心SSB（Solar System Bary⁃center，SSB）和航天器处的脉冲信号到达时间TOA（Time-of-Arrival，TOA）；n为脉冲星在ICRS坐标系中的单位方向矢量。

图1 X射线脉冲星导航原理Fig. 1 X-ray pulsar navigation principle

安装在航天器上的X射线探测器配合相应的信号恢复算法，可以获得tSC。而tSSB可以根据对应脉冲星的相位时间模型进行预测［18］。tSC与tSSB之间的差值Δt便是脉冲信号在航天器与SSB之间沿脉冲星方向传播的时间，也就等价于两点间距离在该脉冲星方向的投影。如果选用3颗不同方向的脉冲星，则通过坐标变换即可得到航天器在ICRS坐标系中的绝对位置。配合卡尔曼滤波等迭代算法即可获得稳定持续的导航信息。

根据几何关系，tSSB和tSC之间的时间差Δt与rsat满足：

考虑到脉冲信号在传播过程中会受到引力延迟效应和周年视差效应等因素的影响，其高阶模型实际上可近似表示为［5］

式中：D为脉冲星到SSB的距离；b是SSB在ICRS坐标系中相对于太阳质心的位置矢量；b和rsat分别为b和rsat的长度模量；G是万有引力常量；Msun是太阳质量。

式（2）便是目前TOA计算应用最为广泛的一种高阶模型，也是脉冲星导航卡尔曼滤波器中的观测模型。而状态模型则可用航天器绕中心天体飞行所满足的动力学方程。对近地航天器而言，其在ECI坐标系中满足的动力学方程为

式中：r=[rx，ry，rz]T；v=[vx，vy，vz]T；μ=GMEarth是地球引力常数；MEarth为地球质量；J2为地球的二阶带谐项；REarth为地球半径。ΔFx、ΔFy、ΔFz为其他天体对航天器的引力摄动，是过程噪声的主要组成部分，f(•)为式（3）中的函数关系。若将系统的状态量x选为航天器在ECI坐标系中的位置r与速度v，观测量确定为tSSB和tSC之间的时间差Δt，则系统的状态空间方程为

式中：w为系统的过程噪声，除其他天体的引力扰动外，还包括太阳光压，地球潮汐等摄动影响；x=[rkvk]T为状态量；z为观测量，即不同脉冲星观测的时间差Δt；h(•)为式（2）等号右侧的函数关系式；V为观测噪声。

为满足线性滤波器的应用，常将式（4）利用雅克比矩阵进行离散并线性化，将式（5）采取近似省略和泰勒展开方式进行线性化。离散线性化后的状态空间方程可表示为［19-20］

式中：Φk|k−1、Gk、Xk、Wk、Zk、Vk分别为离散化后的状态转移矩阵、噪声驱动矩阵、状态量、过程噪声、观测量及观测噪声，且Xk=[rkvk]T=[rxk，ryk，rzk，vxk，vyk，vzk]T；Δti为脉冲星i在航天器与SSB之间的时间差；rsatk−1为离散化后ICRS坐标系中航天器在k-1时刻的位置矢量，rsatk−1为其标量形式；Ek=[rEkvEk]T为离散化后ICRS坐标系中地球的位置及速度矢量；rk、vk为离散化后ECI坐标系中航天器的位置及速度矢量，且满足rsatk=rEk+rk；ni与Di分别为不同脉冲星的单位方向矢量和到SSB的距离；Hk为观测矩阵。

2 误差分析

2.1 星历误差

在国际地球自转服务组织（International Earth Rotation and Reference Systems Service，IERS）2003、2010规范中，分别将DE405和DE421历表作为ICRS坐标系中的动力实现［21-22］。受不同时期观测技术的限制，DE系列星历的精度也是在逐渐提升的。2008年发布的DE421相对于1995年的DE405而言，其定位精度就得到了极大地改善［23］。虽然无法获得天体真实的位置数据，但是通过不同星历数据间的比较作差也能较为直观地展示出精度上的提升。以地球为例，分别利用DE405和DE421计算其从2015-10-1704：00：00到2016-10-1604：00：00在ICRS坐标系中的位置变化情况，采样点间隔设置为5 h。2种星历计算结果间的差值如图 2所示。

通过图 2，基本上可认为DE421相对于DE405轨道误差降低了数十千米。但是DE421仍然是不完美的。其中金星、地球和火星的轨道精度仅为亚千米级，而水星的轨道误差约为数千米，木星和土星更是达到数十千米［12］。

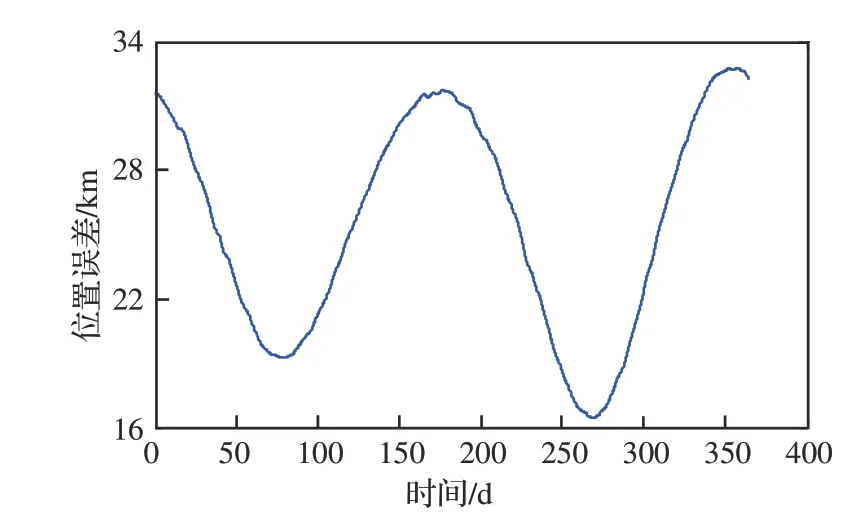
图2 DE405与DE421间地球星历位置误差Fig. 2 Earth position error between DE405 and DE421

根据导航原理和文献［7］的数据分析可以判断，能够对导航结果产生显著影响的主要为中心天体的星历位置误差。因此，本文的星历误差分析均以中心天体的星历位置误差为对象，所涉及的仿真实验均为应用场景最多的近地卫星，星历计算和误差设置也均参考DE421。选择地球以外的其他中心天体或参考星历对本文分析结论并无实质影响。

假设地球真实的位置矢量rE与根据星历计算得到的位置矢量E满足：

式中：δrE为地球星历误差。

若导航系统使用带误差的位置矢量E进行导航解算，便会得到带有误差的观测量Δ：

式中：Δ为带有模型误差的时间差。

由于sat满足：

则此时真实的时间差Δt应当满足［14］：

式中：B为地球星历位置误差导致的模型误差；Γk为地球星历误差的观测矩阵。

目前众多已发表的文献证明，在X射线脉冲星导航的数百乃至上千秒的单个观测周期内可认为天体的星历误差δrE和对应的模型误差B是不变的［7，14-16］。但是长时间来看，这部分误差却因天体运动而存在缓慢且大幅的变化，存在导致算法发散的隐患。

为验证以上分析，利用STK软件产生一条卫星仿真轨道，参数如表 1所示。假设该轨道上运行的某一航天器装有X射线脉冲星导航系统，且其观测的脉冲星为B0531+21、B1821-24、B1937+21，具体参数如表2所示［24-25］。

表1 卫星轨道参数Table 1 Parameters of satellite orbit

表2 脉冲星参数［24-25］Table 2 Parameters of pulsars［24-25］

由于DE421中地球轨道精度为亚千米级，且大小变化受天体周期运动影响大多呈现类似的三角函数关系。因此，本文的数据仿真中假设ICRS坐标系中地球的星历位置误差变化满足：

式中：torbit为地球距离2015-10-1704：00：00的运行时间；Tearth为地球公转一周的时间。

导航使用扩展卡尔曼滤波器（Extended Kal⁃man Filter，EKF），观测周期tobs为300 s，探测器面积等其他导航参数见表 3。初始误差δX0取为［1 km， 1 km， 1 km， 0.02 m/s， 0.02 m/s， 0.02 m/s］。

表3 其他参数Table 3 Other parameters

脉冲星的观测噪声方差σV可确定［5］为

式中：Sdec为有效观测面积；d为Pwidth与Ptime之比。

仿真过程中导航系统的均方根误差（Root Mean Squared Error，RMSE）、地球星历误差、模型误差c·B变化情况如图 3～图 6所示。

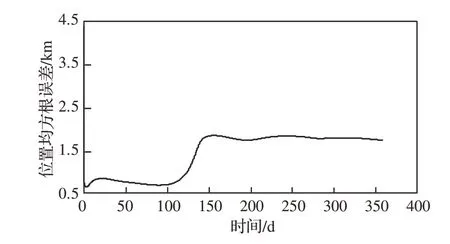
图3 位置均方根误差Fig. 3 Position RMSE of navigation system

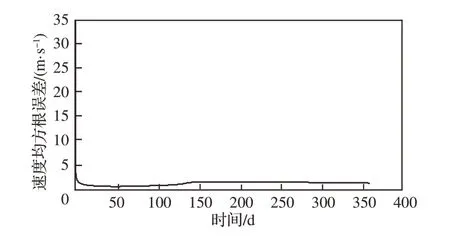
图4 导航系统速度均方根误差Fig. 4 Velocity RMSE of navigation system

表3、图 3～图 6验证了理论分析结果，证明对中心天体星历误差进行实时估计时，有必要考虑算法的跟踪性能，以解决星历误差缓慢变化的影响。

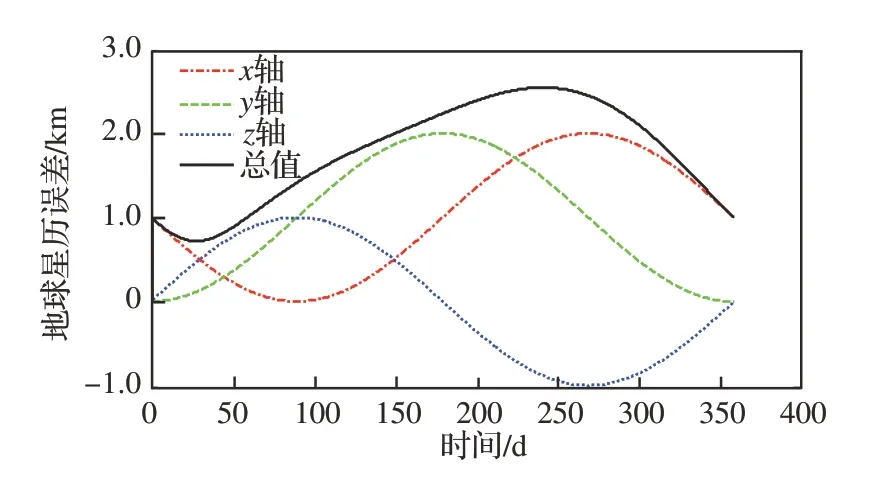
图5 地球星历误差Fig. 5 Earth ephemeris error

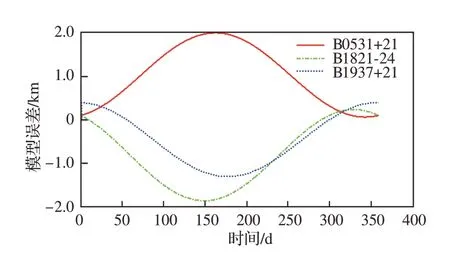
图6 星历误差导致的模型误差Fig. 6 Model errors caused by ephemeris error

2.2 有色噪声

式（4）所示的状态方程中，将地球以外的第三天体引力ΔFx、ΔFy、ΔFz作为白噪声计入过程噪声，实际环境中这部分噪声是难以保证为白噪声的。同样以表1中的卫星轨道为例，利用DE421星历计算卫星受到的第三天体引力。第三天体引力模型为［5］

式中：μ3rd−body为不同天体的引力常量；rsat3rd−body为航天器相对第三天体的位置矢量；r3rd−bodyEarth为第三天体相对地球的位置矢量；rsat3rd−body和r3rd−bodyEarth分别为对应矢量的长度模量。

所考虑的第三天体包括：太阳、水星、金星、火星、木星、土星、天王星、海王星、冥王星及月球。ICRS坐标系中不同轴向的引力摄动及频谱分析结果如图 7和图 8所示。显然，该仿真轨道上的第三天体引力摄动都不符合高斯白噪声的特点。

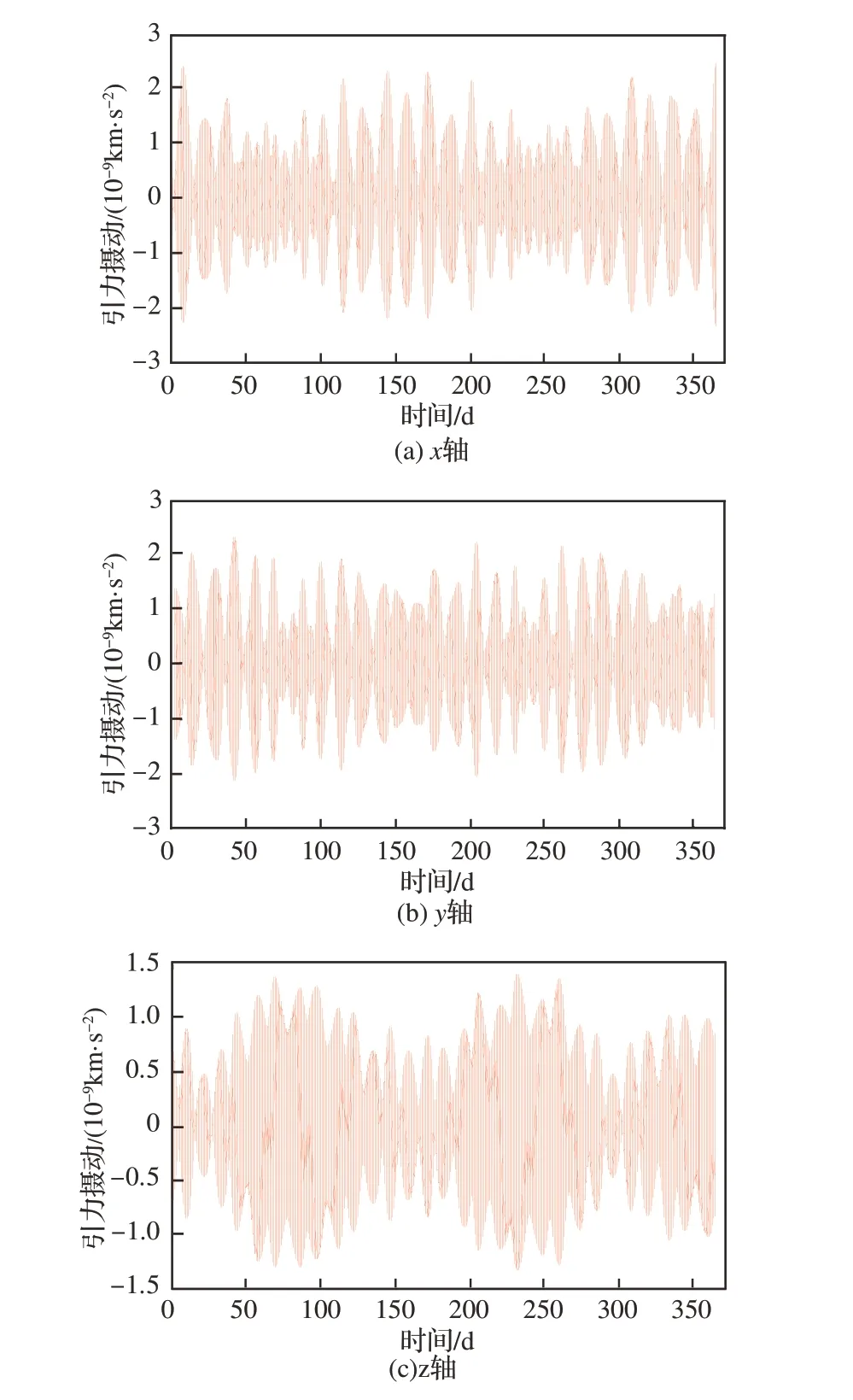
图7 不同轴向引力摄动Fig. 7 Gravitational perturbation in different axes

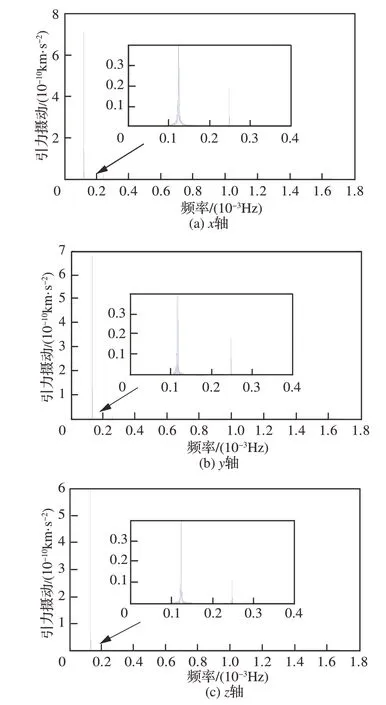
图8 引力摄动频谱分析Fig. 8 Spectrum analysis of gravitational perturbation

对于观测噪声而言，X射线探测器在工作时受自身精度及电流扰动等因素影响，也会产生设备噪声，该部分噪声往往是有色噪声。除此之外，式（2）的高阶模型实际上也是省略了部分高阶项的近似非线性观测模型。省略的高阶项为太阳系内除太阳与地球外其他天体运动对脉冲星观测的影响。结合以上观测噪声的分析，这部分噪声极有可能也为有色噪声。且由于都与第三天体运动有关，还可能出现过程噪声与观测噪声相关的情况。因此，为保证算法的可靠性，有必要针对普通卡尔曼滤波器进行改进设计。

3 TSTDKF算法设计

2级卡尔曼滤波器（Two-stage Kalman fil⁃ter，TKF）的设计初衷便是代替增广算法解决线性系统中的定常偏差问题［26］。它具有收敛速度快、运算量低等优点，也适用于对普通卡尔曼滤波器的优化改进［27］。TKF由2部分组成，第1级为无偏滤波器，实际上是不考虑偏差影响的普通卡尔曼滤波器，第2级为独立偏差滤波器，单独用于实现偏差量的估计及结果补偿。

根据式（11）～式（16）的分析，因Γk作为观测矩阵可根据天体参数实时求解，则可采用2级滤波方法将地球星历误差δrE作为独立偏差滤波器的状态量予以估计。但由于δrE存在缓慢变化的性质，因此在TKF基础上本文设计了TSTDKF滤波器。该滤波器将无偏滤波器改进为一种考虑相关噪声的差分无偏滤波器，并在独立偏差滤波器中添加了多重自适应调节因子以增强其对缓慢变化量的跟踪性能，解决传统TKF只对定常偏差有效的局限性。

3.1 差分无偏滤波器

假设式（6）和式（7）中的过程噪声Wk与观测噪声Vk为满足以下一阶自回归模型的有色噪声：

式中：ξk、ek为互不相关的高斯白噪声，方差分别为σξ、σe；L、J、F均为对角相关系数矩阵，表征有色噪声的相关性强弱；假设此相关系数矩阵均已通过参数辨识等手段获得；当相关系数矩阵均为零矩阵时说明过程噪声与观测噪声为白噪声。

根据以上关系可构造新的观测量Z′k如下所示：

显然此时新构建的观测方程中除HkXk、ξk外均为已知量，而观测噪声也变为了白噪声ξk。但是结合式（22）可见，此时观测噪声与过程噪声仍然存在相关关系。因此，根据式（6）、式（22）及式（24）构建如下方程：

若要求过程噪声与观测噪声不相关，则应当要求变量Ωk满足：

即

式中：I为单位矩阵；HkGkJ+I需满足为非奇异矩阵。

因此，新构建的方程式（25）即可认为是差分无偏滤波器的状态方程。结合式（24），可将新的差分无偏滤波器状态空间方程表述为

式中：Φ′k|k−1为新的状态转移矩阵；W′k为过程噪声，且与观测噪声ξk无关；Ψk为已知输入量。

显然，经过重构得到的状态空间方程满足观测噪声ξk为高斯白噪声，过程噪声W′k与观测噪声ξk无关的条件。但此时的过程噪声W′k仍为有色噪声。由于仅当过程噪声为有色噪声时，对卡尔曼滤波的影响仅体现在状态量一步预测方差PXk|k−1的计算中［28-29］，因此下面结合以上关系推导PXk|k−1新的迭代方程。

定义：

则此时状态量预测方差PXk|k−1应满足：

式中：E（·）为求期望运算。

而根据卡尔曼滤波的迭代关系，重构后的最优估计值应满足如下关系：

即

进而求得协方差PXk−1，W′k为

结合式（21）、式（26）及式（32），可将式（38）整理为

式中：

其中：PVk−2，Vk−1、PQk−1，Qk为对应变量协方差。

同理，结合式（32）可求得PW′k满足：

式中：PVk−1、PQk为对应变量方差。

而根据一阶自回归模型的相关性质可得

将式（38）～式（46）结论代入式（35）即可求得PXk|k−1。

结合以上推导及普通卡尔曼滤波的相关知识，可将差分无偏滤波器的迭代方程总结为

显然，根据Φ′k|k−1、Ψk及W′k的定义，当观测噪声与过程噪声为不相关的白噪声，即L、J、F阵均为零阵时，以上过程退化为EKF。

3.2 强跟踪独立偏差滤波器

结合式（15）、式（28）和式（29），若普通独立偏差滤波器的状态量bk确定为地球星历位置误差δrE，则迭代方程可表述为［30］

式中：Λk为独立偏差滤波器对无偏滤波器状态量的纠正矩阵；Sk和Uk为该级滤波器迭代的中间量；Mk相当于该级滤波器状态量的协方差；为该级滤波器增益矩阵。

通过分析式（57）可以发现，独立偏差滤波器的状态更新仍需用到无偏滤波器的残差信息。对于TKF而言，无偏滤波器的残差变化一定程度体现了独立偏差滤波器状态量bk的变化趋势。因为除噪声因素外，无偏滤波器的残差主要由bk，即系统偏差决定。因此，本文采用无偏滤波器的残差方差作为强化独立偏差滤波器跟踪性能的依据，在增益矩阵的计算中构建多重自适应调节因子λk如式（59）～式（61）所示：

式中：ρ=[ρ1，ρ2，ρ3]为尺度调节参数，可由先验知识确定，无先验知识情况下ρ1、ρ2、ρ3可设置为1；ΔZ′k为根据状态量预测值所确定的观测残差；τ为记忆参数，用于确定λk计算的渐消记忆窗口长度；(•)i，i表示矩阵的第i个对角线元素。

实际上，尺度调节参数ρ是调整在线跟踪性能的指标参数。尺度调节参数越大，跟踪性越强。在已经出现大范围误差的情况下可以更快速的完成误差纠正，但是在已经接近实际结果的稳态下，该参数越大，越会增加稳态下估计结果的波动性。因此，该参数可以在有先验知识情况下进行调整，例如可定期对使用脉冲星导航的卫星轨道进行测定，以确定不同阶段尺度调节参数的大小，进而远程进行参数注入。若偏离误差较大，可适当增加尺度调节参数大小；若已达到误差允许范围内的稳态，可适当减小该值。取值范围一般在（0，50］区间即可。

4 仿真分析

为验证算法的有效性，使用表 1中参数所确定的卫星轨道进行仿真分析，横向比较有色噪声条件下，存在地球星历误差时EKF、TKF及TSTDKF的导航性能。3种算法的观测周期为300 s，位置及速度误差采用均方根误差计算，其他参数仍同表2和表3。对于TSTDFK而言，ρ=[8， 15， 9]，τ=100。

假设观测噪声与过程噪声满足式（21）～式（23）所示的一阶自回归模型，具体参数取值如下所示：

σξ由式（19）确定，σe在2.2节数据分析基础上，综合考虑其他参数的影响设置为

式中：e1=(10−8)2；e2=(10−10)2。

其他相关变量的初始值设置为

当星历误差变化满足式（17）关系时，3种算法的仿真结果对比如图 9所示。通过对图 9的分析可以发现，在噪声相关且存在变化星历误差条件下，TSTDKF的位置及速度均方根误差均低于TKF和EKF。在星历误差估计方面，TSTDKF也比TKF收敛更快，效果更好。

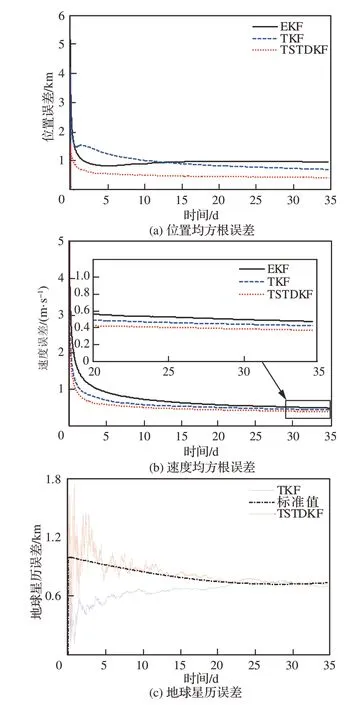
图9 不同算法的仿真结果Fig. 9 Simulation results of different algorithms

为进一步验证算法对地球星历误差的跟踪性能，在相同参数条件下将观测周期延长为1 a，并将星历误差变化趋势在式（17）基础上，增加式（69）、式（70）2种趋势，观察TKF与TSTDKF的跟踪情况，如图 10所示。

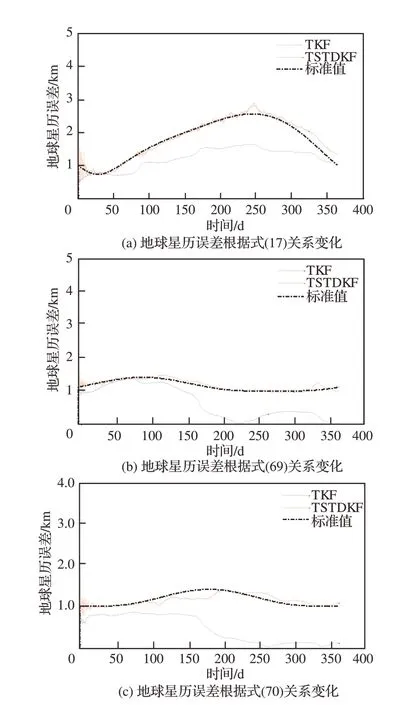
图10 不同算法对星历误差的跟踪情况Fig. 10 Tracking accuracy of ephemeris errors by different algorithms

结合图10，虽然长期来看TSTDKF也会在某些拐点存在一定的失真，但均能够有效纠正，总体精度较为稳定，说明本文所设计的TSTDKF在应对变化的星历误差方面是有效的。

为说明TSTDKF在应对不同噪声情况下的鲁棒性，根据表 4中的实验设置分别对3种算法各进行50次蒙特卡洛仿真，时间30 d。星历误差仍根据式（17）设置，最终不同导航算法的均方根误差统计如表 5所示。

表4 实验条件设置情况Table 4 Setting of experimental conditions

通过对表 5数据的分析可以直观发现：不同噪声条件下，TSTDKF的导航精度均优于其他算法，且性能表现相对稳定；位置误差对噪声条件的敏感度比速度误差高；在实验1条件下，TSTDKF优势最为突出，位置和速度均方根误差分别比EKF提升56.49%和27.66%，比TKF提升35.18%和17.07%；相比于过程噪声，观测噪声为有色噪声时对算法影响更大；在实验5条件下，TKF结果与TSTDKF结果相当。

表5 实验结果统计Table 5 Statistics of experimental results

之所以在实验5条件下TKF和TSTDKF结果相当，是因为各噪声为白噪声时，TSTDKF的无偏滤波器退化为与TKF完全一致。此时两者的差别仅体现在独立偏差滤波器的设计上。而根据图9和图10可见，TKF算法在开始的30 d内虽然收敛较慢，但仍可缓慢地接近标准值。但是长时间运行时TKF往往难以保证较好的跟踪精度，因此随着时间增加，导航误差将会逐渐增大。

这是因为TKF的设计初衷便是应对定常偏差问题。虽然在其他文献中也指出针对缓慢变化的误差具有一定的有效性，但是这仅仅是短期及小范围内。如图9所示，在初期TKF确实可以在一定程度上实现对星历误差的追踪。这是因为地球星历误差变化缓慢且小幅，基本可认为常值。但是随着时间延迟、变化幅度增大，TKF缺乏有效跟踪性能的问题就会暴露，如图10所示。