综合脉冲星时研究进展

杨廷高，高玉平，3，，童明雷，李变，赵成仕，罗近涛，朱幸芝，魏飞

1．中国科学院 国家授时中心， 西安 710600 2．中国科学院 时间频率基准重点实验室， 西安 710600 3．中国科学院大学 天文与空间科学学院， 北京 100049

国 际 原 子 时（International Atomic Time，TAI）是 国 际 计 量 局（Bureau International des Poids et Mesures，BIPM）利用全世界70个守时实验室约460台原子钟和若干频率基准钟构建与保持的时间尺度。协调世界时（Coordinated Universal Time，UTC）与地球自转相位相近似，与TAI只差整数秒。为进一步修正TAI的误差，BIPM每年还对守时与时间比对资料进行事后处理，得到地球时TT（BIPMXXXX），其中XXXX表示发表年份［1-2］。TT（BIPMXXXX）滞后一年才能得到，一般情况下，每年更新一次。为方便起见，如不特别说明，本文也用TT表示TT（BIPMXXXX）。

原子时是积分时间尺度，具有误差累积的特性，影响其长期频率稳定性。基于毫秒脉冲星自转建立的时间尺度称为脉冲星时。射电脉冲星计时观测得到脉冲星脉冲到达时间（Time of Arrival，TOA）。脉冲到达时间测量是以观测站原子钟为参考的，通过时间比对，可将观测站原子钟改正到TAI或TT时间系统。脉冲星TOA测量等效于脉冲星钟与参考原子钟之间的时间比对。但因为脉冲星与地面射电望远镜存在复杂的相对运动，且脉冲星的空间位置坐标与速度、自转参数等是未知的，所以通过TOA测量并不能立刻得到脉冲星钟与原子钟的钟差。只有通过脉冲星TOA数据序列分析，测量得到脉冲星的位置、速度与自转参数，并改正脉冲星与望远镜之间的相对运动影响、星际介质传递的信号延迟以及相对论效应等，才能由TOA计算得到计时残差。理论上，如果所有物理因素（计时参考的原子时误差除外）对TOA影响都消除掉情况下，计时残差可看作脉冲星钟与原子钟比对的钟差时间序列，将此称为脉冲星时。可见，脉冲星时研究与影响TOA的物理因素建模和分析方法是密切相关的。与原子钟不同，各个脉冲星钟的频率稳定性、噪声水平、TOA测量精度（取决于信号强弱与脉冲形状）等是不同的，即便是毫秒脉冲星，不同脉冲星钟性能也会有明显差异。选择自转频率稳定的多颗毫秒脉冲星，采用合适算法构建综合时间尺度，可以进一步消除单星计时噪声以及其他误差影响，以期得到比任何单星都更稳定的时间尺度，即综合脉冲星时。综合脉冲星时建立实际上是更复杂的多颗星计时资料的综合分析过程［3］。通常以国际原子时TAI为参考建立综合脉冲星时（Ensemble Pulsar Time-scale，EPT），得到EPT-TAI时间序列；同样地，如果计时观测以TT为参考，则可以建立综合脉冲星时EPT-TT。

射电天线配置脉冲星计时终端系统就可以实现射电脉冲星计时观测。对选定的一组毫秒脉冲星，按照事先设计好的观测方案，进行长期计时观测的工作模式，被称为脉冲星计时阵（Pul⁃sar Timing Array，PTA）［4-5］。世界上著名的有北美引力波天文台脉冲星计时阵、澳大利亚Parkes脉冲星计时阵、以及欧洲5个射电望远镜联合组成的脉冲星计时阵。世界上的脉冲星计时阵联合起来，被称为国际脉冲星计时阵（International Pulsar Timing Array，IPTA）［6-8］。至今，IPTA已经长期坚持60多颗毫秒脉冲星计时观测，其中部分毫秒脉冲星已积累20年以上的资料。2016年IPTA公开释放了49颗星的数据［9］。2019年又第二次公开释放了65颗毫秒脉冲星数据，其中包括第一次释放后的新观测数据［10］。在中国，中国科学院国家天文台、上海天文台、新疆天文台、云南天文台与国家授时中心负责或参与合作观测的5个中小口径射电望远镜的脉冲星计时观测，也已经积累了多年的计时观测资料。近年来，中国500 m口径射电望远镜（Five hundred meters Aperture Spherical Radio Telescope， FAST）已经投入毫秒脉冲星计时阵观测项目，其计时观测精度比IPTA有显著提高。

国际上，利用IPTA资料，已经发表了综合脉冲星时的研究结果。中国学者采用不同算法也取得了类似的结果。射电脉冲星计时观测原始数据经过处理，才能得到以原子时为参考的TOA［11-12］。脉冲星计时观测得到的TOA序列可表示为计时模型信号、计时噪声（包括白噪声与红噪声）和有关系统误差的叠加［13］。用向量d表示脉冲星TOA序列数据，向量τTM表示计时模型信号，τWN表示白噪声，τRN表示脉冲星自转红噪声，τDM表示星际介质色散延迟，τCLK表示参考原子时误差，τEPH表示太阳系天体历表误差，τGW表示引力波信号，有

其中计时模型信号通过脉冲星星历参数拟合确定（见第1节），各个脉冲星的白噪声与红噪声参数采用专门设计的研究方法确定（见2.1.1节）。

星际介质色散延迟与色散量参数（Disper⁃sion Measure，DM）（描述脉冲星至观测站电子柱密度的参数）及其随时间的变化有关。DM及其变化由多个观测波段的TOA数据分析研究确定［14-15］。这些物理量对不同脉冲星而言，是彼此独立的，被称为各个脉冲星的独立参数。计时观测参考原子时误差、太阳系天体历表误差和引力波信号与不同脉冲星之间具有各自不同的相关性［16］。这些参数被称为脉冲星计时阵的公共参数，必须用脉冲星计时阵包括的多颗脉冲星的TOA序列分析研究确定。这些公共参数是需要提取的信号，公共参数探测与研究是IPTA的重大科学目标。脉冲星各个独立参数的测量误差会影响公共参数的确定精度。因而，在研究公共参数时，根据具体情况设计合适的算法是非常重要的。通常的做法是，利用长序列（一般5年以上）TOA资料和TEMPO2软件包［17］，先拟合得到每颗脉冲星的近似计时模型参数与DM参数，再用剩余的计时残差序列，设计合适的研究方案，进一步精密分析各个脉冲星的独立参数与感兴趣的公共参数。

由于主要目的是构建综合脉冲星时，也就是说，希望利用脉冲星计时阵长期计时残差序列，提取出参考原子时的误差信号，即综合脉冲星时与计时观测参考原子时差值的时间序列信号。为此，在构建综合脉冲星时的时候，必须精确测量每颗脉冲星的独立参数，并尽量设法消除观测设备变化、太阳系天体历表误差与引力波信号扰动的影响。利用国际脉冲星计时阵长期TOA资料研究表明，近年来新发布的太阳系天体历表仍存在不可忽略的系统误差，引力波信号基本上是属于比原子时误差更难测量的弱信号［13］。在脉冲星计时阵中，原子时误差是单极性的，与所有脉冲星具有相同的相关性；太阳系天体历表误差是二极性信号，对于脉冲星计时阵中位于相反空间方向的2颗脉冲星而言，太阳系历表误差对二者计时残差的影响大小相等、符号相反；引力波是更复杂的四极性信号，其对计时残差的影响是计时阵中两两脉冲星对相对于观测站张角的函数。以上3种公共参数具有各自可识别的特征［13］。设计合适的综合脉冲星时算法，完全能够有效提取出原子时误差信号，并尽量消除太阳系天体历表误差与引力波扰动的影响。

构建综合脉冲星时还需要尽量消除计时噪声影响。各个脉冲星具有不同特征的红噪声，其主要来自于自转的不稳定性，也与没有消除掉的DM变化有关。多数毫秒脉冲星由于自转不稳定引起的红噪声是弱红噪声。DM随时间变化的不确定性与星际介质的散射效应是射电计时观测的主要误差源［18-19］。DM变化的精确测量需要同时进行多个不同波段的TOA观测。由于DM引起的信号延迟与观测频率的平方成反比，因而DM不确定性对低频观测影响最大。鉴于此，低于1000 MHz频率的计时观测主要用于DM测量，但对于脉冲星时研究难以做出重要贡献［20］。有的计时资料，由于没有充分的多波段观测数据，DM误差会与计时红噪声混淆，无法将二者区分开。

观测数据预处理是脉冲星时研究分析的必要步骤，其中包括每颗脉冲星计时模型参数初步拟合、DM及其变化影响的消除、TOA测量误差的校准和计时红噪声模型参数近似估计等。观测数据预处理后得到的每颗脉冲星的计时残差基本消去了DM与观测系统变化等因素的影响，但包括有每颗星的计时噪声与计时阵的共同信号［10］。精确的预处理，有时可以在某种程度上简化综合脉冲星时算法。目前，综合脉冲星时算法有基于TEMPO2软件的广义最小二乘拟合、基于TEMPO2与TEMPONEST软件的贝叶斯分析方法和维纳滤波算法。

本文第1节将概述脉冲星计时模型参数拟合原理。第2节重点描述综合脉冲星时的3种算法。在第3节给出综合脉冲星时的主要研究结果与比较。第4节是有关综合脉冲星时研究的总结与讨论。

1 脉冲星计时模型参数拟合原理

脉冲星自转频率及其对时间的导数称为脉冲星自转参数；脉冲星的赤经、赤纬、自行与视差，对于双星系统还包括双星轨道参数等称为脉冲星天体测量参数，这些参数又统称为计时模型参数或脉冲星星历参数。观测到的TOA与脉冲星脉冲辐射时刻之间的转换关系用计时模型描述［21-22］。由于恒星际介质与太阳系行星际介质的色散效应，还需要利用测得的DM参数对不同频率观测的TOA进行色散延迟修正［14-15］。利用射电计时观测资料拟合脉冲星计时模型参数，必须精确知道射电望远镜相对于地球质心的三维坐标，同时，还需要知道观测时刻地心相对于太阳系质心的位置坐标与速度（由已知的太阳系天体历表提供）。

在脉冲星参考架，脉冲星脉冲发射时刻tp与其自转参数关系可表示为

式中：t0是参考历元；t和t0是脉冲星时；φ0、v和v̇分别是t0时刻脉冲星的自转相位、频率及其一阶导数。假设tobs是以原子钟为参考，地面射电望远镜观测得到的脉冲星脉冲TOA，tobs与tp之间有下述关系：

其中：ΔtC包括计时观测站原子钟到国际原子时的改正和国际原子时到质心坐标时（Time of Barycentric Coodinates， TCB）的改正［23-25］，这2项改正通常采用事先计算好的数值表内插得到；c是光速；n是脉冲星在（太阳系）质心坐标系的单位矢量；V是脉冲星相对于太阳系质心速度矢量；Δt=t−t0，即观测时刻与参考历元差值；s是观测时刻望远镜相对于太阳系质心的位置矢量；DM是色散量；vg是计时观测频率；k是色散常数，k=2.41×10−16Hz−2·cm−3·pc·s−1（pc为秒差距Par⁃sec缩写）；R0是参考历元脉冲星相对于太阳系质心距离；G是牛顿引力常数；Mj是第j个太阳系天体的质量；sj是在观测时刻望远镜相对于第j个太阳系天体位置矢量；sj是sj是的模；n是计算Shap⁃iro延迟采用的太阳系主要天体数量；sΘ是观测时刻望远镜到太阳的距离；mΘ是太阳质量；Ψ是太阳和脉冲星在观测时刻相对望远镜的张角。

式（3）中，tobs（观测得到的TOA）和s（望远镜相对于太阳系质心矢量）为已知量，其中s由望远镜相对地心位置矢量（事先已知），利用地球自转参数、岁差、章动和太阳系天体历表提供的地心相对于太阳系质心位置坐标计算得到［21］。式（3）右边第3项是由于望远镜相对脉冲星运动引起的脉冲信号延迟改正，称作Roemer延迟，第4项是视差改正项，第5项是与脉冲星速度有关的一阶多普勒改正，第6项是与观测频率有关的色散延迟改正，第7项是脉冲星加速度引起的改正，第8项与第9项是Shapiro延迟改正，式（3）最后一项Δtob是脉冲双星轨道运动延迟改正，包括轨道运动的Roemer延迟、Shapiro延迟和时间坐标相对论改正等［21］。

脉冲信号的真空传播延迟包括由于相对运动引起的随时间变化分量和不变的常数分量。式（3）只计算延迟随时间变化的分量，忽略常数分量，虽然常数分量是个很大的数值。另外，式（3）还应该包括观测系统（设备）变化引起的TOA跳变。脉冲星在参考历元t0的自转相位φ0、自转频率v及其导数v̇是待求的自转参数。对于毫秒脉冲星，自转频率的二阶导数可以忽略，但对于自转较慢的普通脉冲星，自转参数还应该包括自转频率的二阶及其以上高阶导数。式（3）中脉冲星位置矢量（包括方向和距离）以及运动速度参数与通常采用的脉冲星赤经、赤纬、自行与视差参数之间具有确定的转换关系，这些是待求的天体测量参数［26-27］。脉冲星计时观测只能测量自行，不能测量视向速度。对于脉冲双星，待求的参数还应该包括脉冲星的轨道参数以及可能测量的后开普勒参数［28-31］。

通常脉冲星计时模型参数的近似值总是知道的，对于小量参数，如脉冲星自转频率的导数等，其近似值可设为0。将参数近似值作为采用值分别代入式（2）和式（3），利用脉冲星的长期计时观测得到的TOA时间序列（n个TOA），可以计算得到每个TOA的计时残差。在忽略脉冲星红噪声情况下，计时残差的系统性变化被认为是由脉冲星参数采用值误差所致。利用脉冲星计时残差（称为拟合前残差）采用最小二乘拟合，可以进一步得到脉冲星参数采用值的改正值及其协方差。最小二乘拟合需要将非线性方程式（3）在各个参数采用值处进行级数展开，从而把式（3）转换成包含脉冲星参数采用值误差的线性方程。假设R向量是拟合前的计时残差，脉冲星参数采用值的误差向量为P，脉冲星参数的系数矩阵（也称为计时模型矩阵）为M，如果观测TOA数量为n，脉冲星参数总数量为m（n>m），则M是n×m的矩阵。用矩阵表示的最小二乘拟合的线性方程为

式中：E是拟合后的计时残差向量。参数的最小二乘解为

通过迭代，利用式（4）可以得到更精确的脉冲星参数解及其协方差。实际上，考虑到各个TOA测量误差不同，需要利用式（4）采用加权最小二乘求解，权取为1σ2i，σi是第i个TOA的误差，称为白噪声（与观测时间无关的噪声）。另外，考虑到脉冲星红噪声（与观测时间相关的随机噪声）影响，脉冲星计时模型参数拟合往往采用更复杂的算法（见2.1节）。TEMPO2软件及其插件是国际上进行脉冲星计时分析的基础性软件系统。

2 综合脉冲星时算法概述

综合脉冲星时算法的基础是正确拟合脉冲星计时模型参数，以便得到每颗星的计时残差。构建综合脉冲星时，就是从多颗脉冲星计时残差提取参考原子时误差信息的过程。在毫秒脉冲星计时观测初期，学者采用加权平均方法计算综合脉冲星时。将计时残差近似看作包含计时噪声和综合脉冲星时信号的时间序列。通过多颗脉冲星计时残差加权平均，进一步消除脉冲星计时噪声，从而得到综合脉冲星时［32］。随着脉冲星数量增加与计时观测精度提高，综合脉冲星时算法逐步趋于改进、优化与完善。

2.1 基于TEMPO2软件的广义最小二乘拟合算法

2.1.1 脉冲星计时模型参数的广义最小二乘拟合

脉冲星计时观测在一定积分时间内得到积分脉冲轮廓。利用相同波段大量观测平均建立模板脉冲轮廓。积分脉冲轮廓与模板脉冲轮廓拟合得到TOA，同时也提供TOA的拟合误差［12］。实际上，观测得到的TOA的不确定性比其拟合误差要复杂得多，TOA拟合误差往往不能反映TOA观测的真实误差。首先，由于星际闪烁效应，实际观测得到的脉冲强度随时间迅速变化，从而导致在不同时刻的观测信噪比是不同的［33］。另外，脉冲星辐射的脉冲形状具有抖动（Jitter）现象，TOA的不确定性还应该包括脉冲形状抖动引起的误差。假设第i个TOA的脉冲轮廓拟合误差为>σi，为其估计的真误差，二者具有下述关系：

式中：EFAC是比例因子；EQUAD是代表脉冲抖动的参数。这2个参数可以针对脉冲星每个观测系统数据，应用TEMPO2插件EFACEQUAD分析确定［20］。利用可以构建白噪声协方差矩阵（对角线元素是每个TOA的方差，矩阵的其余元素为0）。

用脉冲星长期计时资料拟合脉冲星模型参数还应该考虑到红噪声与DM变化影响。假定DM变化影响已经消除，只讨论红噪声存在情况下脉冲星参数拟合问题［34］。红噪声只取决于脉冲星，与观测频率无关。利用式（4）得到拟合后计时残差，除去白噪声以外，拟合后计时残差还包含有与时间相关的红噪声。用幂律模型描述拟合后计时残差功率谱密度［35-36］：

式中：P0是功率谱幅度；γ是谱指数；f是傅里叶频率；fc是红谱与白谱交叉点（拐点）的傅里叶频率。

利用TEMPO2的SPECTRALMODEL插件，由计时残差分析确定式（7）的参数，从而得到理论功率谱。再对理论功率谱进行傅里叶变换，可以得到反映红噪声影响的计时残差的协方差函数，进而构建红噪声协方差矩阵。将红噪声与白噪声协方差矩阵之和表示为C，则脉冲星计时模型参数的广义最小二乘解可表示为

对C进行Cholesky分解，得到矩阵U，C=UUT。用矩阵U−1分别对R和M进行归一化和白化，即定义RW=U−1R，MW=U−1M，则脉冲星计时模型参数的广义最小二乘解也可表示为

式（9）与普通最小二乘解表达式（5）具有相同的形式，其解与式（8）结果相同。为方便起见，TEMPO2应用式（9）求解。如果脉冲星红噪声的功率谱计算是正确的，用Cholesky分解计算得到的RW的功率谱应该是白谱，则式（9）结果是正确的。否则，需要迭代运算，以便求得精确的脉冲星参数解。经验表明，在大多数情况下，迭代过程收敛很快，往往只需一次或二次迭代就能获得正确结果。与普通最小二乘方法相比，广义最小二乘解析表达式包括了与计时噪声相关的协方差矩阵，能够有效避免计时噪声对计时模型参数拟合的影响，从而得到更精确的脉冲星参数及其协方差［36］。由于该方法必须对每颗星进行谱分析，该算法又称为频率分析方法。

为拟合并消除DM变化影响，一般情况下，还需要利用多个波段的TOA序列数据，在采用广义最小二乘拟合脉冲星计时模型参数时，再增加DM随时间变化的参数。在考虑到计时噪声情况下，同时拟合得到脉冲星计时模型参数与DM变化参数［15］。DM变化参数模型采用等时间间隔采样的线性模型，并增加约束条件，使得所有采样点DM变化值的和等于0。在测量DM变化时，必须计及红噪声对DM测量的影响。有关DM变化测量的详细描述，请参考文献［15］。

以上描述的单颗脉冲星计时模型参数求解方法可以推广到多颗脉冲星同时求解的情况，目的是分析研究多颗脉冲星的公共参数，如参考钟误差等。首先需要将每颗星的计时残差按照脉冲星编号顺序组合在一起，形成包含所有脉冲星的计时残差向量。将待拟合的公共参数与每颗脉冲星的独立参数依次组合成总参数向量，利用每颗脉冲星参数的采用值与公共参数数学模型计算得到总参数的系数矩阵。在计及每颗脉冲星白噪声与红噪声情况下，采用广义最小二乘同时拟合每颗脉冲星计时模型参数与公共参数。为简化计时残差协方差矩阵计算，每颗脉冲星的白噪声与红噪声参数可采用单星计时分析的结果，在此基础上构建初步的总计时残差的协方差矩阵。然后应用广义最小二乘迭代求解。

2.1.2 包括脉冲星钟误差参数的广义最小二乘拟合算法

脉冲星计时观测参考的原子时系统误差就是要提取的综合脉冲星时信号，简称为钟误差信号。钟误差是脉冲星计时阵中所有脉冲星计时残差中都包含的共同信号。只要建立能够描述钟误差信号的数学模型，在每颗脉冲星独立参数（计时模型参数）的基础上，进一步增加钟误差公共参数，就能够利用脉冲星计时阵多颗脉冲星的长期观测资料，采用广义最小二乘拟合算法，同时拟合得到每颗脉冲星的独立参数与综合脉冲星时参数。描述综合脉冲星时最简单的数学模型就是对其信号按照时间进行等间距采样。因要提取的信号是低频信号，其采样间隔可根据观测TOA采样平均间隔设计为半年或90 d等。因钟误差随时间呈现缓慢变化趋势，在其信号的每个采样间隔内，再采用线性内插法提取每个采样点的信号［3，15，20］。

对于包括脉冲星钟误差参数在内的多颗星计时分析的广义最小二乘算法，组合得到的包含所有脉冲星的总计时残差向量为Rtot（假定Rtot已经消除了每颗脉冲星DM变化的影响），包括钟误差模型参数与每颗脉冲星计时模型参数（参数采用值的改正值）的总参数向量为Ptot，待拟合的所有参数的总系数矩阵为Mtot。于是，可得如下线性方程：

式中：Etot是拟合后总计时残差向量。

应该指出的是需要拟合的综合脉冲星时参数与脉冲星某些计时模型参数具有相关性。从式（2）和式（3）可以看出，钟误差随时间的变化与脉冲星自转频率及其一阶导数相关，钟误差的周年变化与脉冲星的位置、自行参数相关。为尽量减小这种相关性影响，需要在最小二乘方程式（10）的基础上再增加以下约束条件方程［15，37］：

式中：ΔC(ti)是综合脉冲星时信号在ti（i=1，2，…，n）时刻的采样值；ϖ=2π年。加入这些约束条件，将综合脉冲星时信号与计时模型参数（主要是自转参数与脉冲星位置参数）的协方差减到最小。这些约束条件方程式连同式（10）共同构成如下最小二乘方程式：

其中：B是描述约束条件的矩阵；RB是约束条件向量，根据式（11）～式（15），有RB=0；EB向量是约束条件方程的拟合后残差。式（16）是利用多颗脉冲星同时拟合综合脉冲星时信号与每颗脉冲星各自计时模型参数的基本最小二乘方程。考虑到脉冲星计时观测不可忽略的白噪声与红噪声，还需要计算总计时残差的协方差矩阵（包括白噪声与红噪声的协方差矩阵），并采用广义最小二乘法同时拟合得到综合脉冲星时与每颗脉冲星的计时模型参数（见2.1.1节）。

随着脉冲星数量增加，计时残差向量长度大大增加，待拟合的参数也更多。在这种情况下，为简化广义最小二乘拟合过程，最好应用广义最小二乘法，首先单独分析得到每颗脉冲星的计时噪声参数与计时模型参数。然后，将每颗星的噪声参数用作计算多颗星总协方差矩阵的采用值，将每颗脉冲星的天体测量参数作为已知量，于是，式（16）中待拟合的参数向量Ptot只包含综合脉冲星时参数与每颗星的自转参数［20］。由于待拟合参数相对减少，拟合过程更易操作，也能够保障取得可靠的综合脉冲星时结果，但一至二次迭代过程是必要的。

在广义最小二乘拟合算法中，因引力波、太阳系行星历表误差对计时残差影响具有与综合脉冲星时不同的特征，在很大程度上能够削弱二者对综合脉冲星时信号的影响。

脉冲星TOA的非均匀采样、各个脉冲星观测总时间跨度不同，再加上综合脉冲星时参数的线性内插，会导致其信号的各个采样点之间具有不同程度的相关性［3，20］。在广义最小二乘算法输出的总参数向量的协方差矩阵中，综合脉冲星时各个采样点之间的协方差能够反映这种相关性。各采样点方差的平方根是综合脉冲星时数值本身的1σ误差。

2.2 综合脉冲星时贝叶斯算法

综合脉冲星时的贝叶斯算法，是在脉冲星计时分析贝叶斯方法的基础上发展起来的一种算法。脉冲星计时分析贝叶斯方法基于贝叶斯推论，能够同时估计脉冲星计时模型参数与计时噪声模型参数［38-42］，其基本分析软件为TEMPONEST［40］。

2.2.1 贝叶斯推论原理

贝叶斯推论表示为

式中：Pr(Θ|D，H)≡Pr(Θ)是给定观测数据D和物理模型H情况下，模型参数Θ的后验概率分布密度；Pr(D|Θ，H)≡L(Θ)是似然函数，即，给定物理模型及其参数情况下，观测数据的概率分布密度；Pr(Θ|H)≡π(Θ)是给定物理模型情况下，模型参数的先验概率分布密度；Pr(D|H)≡Z是贝叶斯证据。贝叶斯证据与参数Θ无关，因此，用式（17）估计模型参数时，可以忽略贝叶斯证据项（即假设其值是1）。

为估计模型参数Θ，需要采用合适方法从参数的后验概率分布对参数进行采样，例如采用标准马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）采样方法，再从参数Θ的大量采样样本统计得到参数估计值及其误差。为计算参数Θ的后验概率分布，其先验概率分布是必须知道的，一般可假定为均匀分布。贝叶斯证据对模型选择起决定作用。例如，对于同一观测数据D，为比较2个模型的优劣，需要分别计算这2个模型的贝叶斯证据Z，通常Z值较大的模型更优越。如果两模型的Z值接近，则优先采用参数较少、相对简单的模型。贝叶斯证据计算公式为

式中：n是参数空间的维数，显然描述模型的参数越多，证据计算越繁重。国际上已经建立的MULTINEST算法能够有效进行脉冲星模型参数后验概率分布采样，也能同时计算并给出贝叶斯证据［40，42］。

2.2.2 脉冲星计时似然函数

应用贝叶斯方法进行脉冲星计时分析，首先需要写出贝叶斯公式式（17）中的似然函数表达式。下面按照从简单到复杂的3种情况，分别导出观测数据TOA向量d的似然函数［40］。

1）假设d=τTM(ε)+τSTO，τTM(ε)是计时模型参数向量ε的函数，代表确定性的计时模型信号。τSTO是服从高斯过程的随机分量，对于第i个TOA，其不确定性σi代表随机分量。假设TOA数量为n，计时观测的似然函数可写为

式（19）是贝叶斯分析方法最简单的只包括脉冲星计时模型参数的似然函数表达式。

2）为正确描述脉冲星TOA白噪声，和2.1.1节的讨论一样，需要引入σi的2个修正因子EFAC与EQUAD。修正σi后的白噪声为

式中：α和β分别代表EFAC和EQUAD参数。注意式（20）与式（6）是不相同的，包括脉冲星计时模型参数与白噪声参数的似然函数表达式为

3）下面讨论再进一步包括脉冲星计时红噪声的情况。用幂律模型表示脉冲星红噪声的功率谱密度［20，38，40，43］为

式中：Ared是红噪声的幅度；γred是谱指数，二者是红噪声功率谱模型参数；fc=1/年。计时观测的协方差矩阵由红噪声协方差矩阵与白噪声协方差阵构成。红噪声的协方差矩阵的计算式为［20］

其中：下标i、j表示第i、第j个计时TOA，tij是第i和第j个TOA时刻的差值。积分下限频率为1T，T是TOA的总时间跨度。低于1T的傅里叶频率分量，在脉冲星自转参数拟合时被吸收到自转参数中了。白噪声的协方差矩阵用修正后的白噪声构建，是对角线矩阵N。单颗脉冲星计时观测的总协方差矩阵为C=N+Cred，Cred为红噪声协方差矩阵。于是，同时包括计时模型参数、白噪声与红噪声参数的计时观测似然函数表达式为

对于单颗脉冲星计时分析，用式（24）代替贝叶斯公式（17）中的L(Θ)项，可以用贝叶斯方法估计得到计时模型参数、白噪声、红噪声参数及其误差。和红噪声一样，DM变化的功率谱也可以用幂律模型描述。对于单颗脉冲星多个波段的观测资料，还可以写出再包括DM随时间变化参数的似然函数，从而在分析脉冲星计时模型与噪声参数的同时，也分析DM变化参数［14］。和最小二乘分析方法类似，脉冲星计时的贝叶斯分析也要求事先知道脉冲星各类参数的近似值。如果只对某类参数感兴趣，可以将其他参数边际化［38］，集中分析感兴趣的少数参数。

上述单星计时分析的3个似然函数表达式式（19）、式（21）和式（24）中，计时模型参数与TOA关系都是式（3）描述的非线性关系，贝叶斯方法能够用非线性分析方法直接求解脉冲星计时模型参数与计时噪声参数。如果先用TEMPO2软件对TOA序列数据（d向量）采用最小二乘方法（见本文第1节）得到初步拟合后计时残差δtpost与计时模型参数近似估计值，然后，用δtpost−Mδε（δε是脉冲星计时模型参数近似值的改正值，M是计时模型参数的系数矩阵）代替式（19）、式（21）和式（24）中的d−τTM(ε)，则这3个似然函数表达式中，计时模型就变成线性近似的形式了。用贝叶斯方法基于线性近似计时模型的似然函数表达式，也可以正确地求解脉冲星计时模型参数与计时噪声参数。在同时对多颗脉冲星资料进行分析时，采用线性近似计时模型更方便。在下面讨论综合脉冲星时贝叶斯算法时，采用脉冲星计时模型线性近似的分析方法。

2.2.3 综合脉冲星时的贝叶斯算法

原理上，贝叶斯方法可以扩展为基于多颗脉冲星在多个频率的长期计时观测资料，同时分析各个脉冲星计时模型参数、计时噪声参数、DM变化模型参数、综合脉冲星时参数、太阳系行星历表误差参数与引力波参数等的综合性分析方法。与单星分析相比，多星分析的参数数量急剧增加。不仅物理模型更复杂，且贝叶斯算法计算量更大，耗费计算时间更多。贝叶斯方法又可细分为多种不同具体算法，包括时域分析算法和时-频域分析算法［40-41］。不同算法的差异主要是各类噪声信号数学描述的不同。另外，还研究发展了从多维空间后验概率分布密度采样的不同方法，以便提高采样速度与可靠性［41］。

贝叶斯方法用幂律功率谱模型描述综合脉冲星时信号的功率谱，用最大似然估计方法估计综合脉冲星时信号模型参数，再用估计得到的信号模型参数重构脉冲星时信号波形。

为方便综合脉冲星时研究，首先用TEMPO2软件针对每颗毫秒脉冲星长期计时观测TOA序列进行分析，得到每颗星拟合后计时残差δtp，post与计时模型参数的初步估计值。假设拟合后计时残差已经消除了DM误差影响，所以，每颗星拟合后残差主要包括计时噪声与感兴趣的钟误差信号。参考式（24），对于单颗脉冲星，拟合后计时残差的线性计时模型形式的似然函数可表示为

式中：n是残差数；C是计时残差的协方差矩阵（白噪声与红噪声协方差矩阵之和）；Mp是计时模型参数的系数矩阵（计时模型矩阵）；δεp是计时模型参数改正值。

为求解综合脉冲星时信号，需要将单颗脉冲星的似然函数表达式扩展到多颗脉冲星，并包括参考钟误差（综合脉冲星时）信号的情况。将多颗脉冲星计时残差按照脉冲星顺序组合在一起，构成总的计时残差向量。一般情况下，多颗脉冲星计时残差能够近似覆盖共同时间段。原理上，在同一时间段内观测的星数越多，TOA数据越密，提取的钟信号误差会越小，反之则误差较大。各个脉冲星红噪声用式（22）幂律模型描述，彼此相互独立。作为所有脉冲星共同信号的综合脉冲星时功率谱也用幂律模型描述［20，43］，有

式中：Aclk（谱幅度）与γclk（谱指数）是需要用贝叶斯分析方法求解的钟信号参数。因为各个脉冲星计时模型参数改正值是线性的，其函数形式已知，可以解析地将每颗脉冲星计时模型参数边际化［38-39］。只包含综合脉冲星时与各个脉冲星计时噪声参数的多颗星总计时残差向量δt的似然函数可表示为［20，43］

式中：δt=δtpost−M(δε)，δtpost是多颗星拟合后总计时残差向量，δε是按顺序组合在一起的多颗星的计时模型参数改正值，M是δε的系数矩阵；I、J表示第I、第J颗脉冲星，i、j是指每颗脉冲星的第i、第j个残差；Ctot=CW+CTN+Cclk，其中Ctot是多颗脉冲星计时残差的总协方差矩阵，CW、CTN和Cclk分别是多颗星计时残差的白噪声、红噪声和综合脉冲星时信号的协方差矩阵。因为各个脉冲星的计时噪声是彼此独立的，当I≠J时，CW，I，J=0，CTN，I，J=0。综合脉冲星时是所有星的共 同 信 号，有Cclk，I，J，i，j=Cclk，i，jCclk，I，J，当I≠J时，Cclk，I，J=1。式（27）中有：

因为感兴趣的是综合脉冲星时参数，用贝叶斯方法计算综合脉冲星时幂律谱模型参数Aclk和γclk的后验概率分布时，还可以采用数值方法将式（27）中的其他噪声模型参数边际化［38-40］。由边际化的后验分布，用合适采样方法，得到脉冲星时幂律谱模型参数及其误差估计。综合脉冲星时谱模型参数确定后，就知道了与综合脉冲星时有关的总计时残差的协方差矩阵，进而可以用非等间隔采样的广义维纳滤波方法构建综合脉冲星时波形与协方差矩阵［20，43］。还可用广义维纳滤波内插信号采样数据点，如内插成等间距数据点，或外推预报信号数据点［14，44］。综合脉冲星时信号的波形及其协方差的计算式为

受计时残差δt误差影响，由式（29）得到的综合脉冲星时clk包含有不可忽略的高频噪声，进一步滤除高频噪声是必要的。

2.3 综合脉冲星时维纳滤波算法

脉冲星计时观测TOA序列利用TEMPO2正确拟合脉冲星计时模型参数后的残差，进一步经过预处理后，得到按采样时间均匀分布的计时残差序列，记为观测残差向量rI，下标代表第I颗脉冲星。rI包含脉冲星时信号、计时噪声与其他弱扰动信号（如太阳系行星历表误差、引力波）。令Qss表示与综合脉冲星时信号有关的计时残差的协方差矩阵，QrI表示残差向量rI（包括信号与噪声）的协方差矩阵，wI是第I颗脉冲星归一化的权重。假设共n颗脉冲星，则综合脉冲星时信号的最佳估计为［45-46］

维纳滤波的关键是如何从多颗脉冲星各自的残差向量rI估计QrI和Qss。首先需要估计协方差函数，然后由协方差函数构建协方差矩阵。显然，至少具有2颗以上脉冲星的观测才能估计共同信号的协方差函数。对于n颗脉冲星，可组成m个相互独立的脉冲星对，这里m=n(n−1)/2。由每个脉冲星对估计得到其脉冲星时信号（脉冲星对的共同信号）的互协方差函数。再由m个信号互协方差函数的平均得到综合脉冲星时信号的平均互协方差函数，进而得到Qss。由于不同脉冲星的计时噪声是互相独的，平均互协方差函数能够较好地消除各个脉冲星计时噪声的影响，也能最大程度地消除其他弱扰动信号影响。再由每颗脉冲星残差向量rI分别估计它们各自的自协方差函数，进而得到QrI。

脉冲星的自协方差与互协方差函数计算采用下述算法［45］。将脉冲星残差向量rI进一步表示为rI，L，下标I表示第I颗脉冲星，下标L是残差向量的第L个数据点，N是向量rI，L的长度，令δ为计时残差采样间隔，第I颗星残差向量的傅里叶变换为

式中：hL是残差向量的平滑窗函数，选择合适的平滑窗函数可以尽量减小频谱渗漏的影响［36］。n颗脉冲星的自功率谱（I=K）和互功率谱（I≠K）的计算式为

式中：(·)*表示复数共轭运算。自协方差（I=K）与互协方差（I≠K）的计算式为

其中：N表示第N个傅里叶频率。

等间距采样的维纳滤波算法利用脉冲星对的计时残差向量，通过互相关提取共同的综合脉冲星时信号，进而通过多个脉冲星对取平均，进一步消除红噪声、引力波与太阳系行星历表误差影响。维纳滤波方法相对简单，易于实施。但按照上述维纳滤波算法得到的综合脉冲星时仍然包含较强的高频噪声（主要来自于脉冲星计时残差向量rI），还需要设计合适滤波器，进一步滤除高频噪声［45］。

3 综合脉冲星时研究结果

因综合脉冲星时研究需要多颗毫秒脉冲星长期计时观测资料，在21世纪初，只有2颗约连续8年的计时观测资料及研究结果发表。利用这2颗星数据的综合脉冲星时研究主要是加权平均与维纳滤波方法［32，45-46］。结果表明，以TAI为参考的综合脉冲星时频率稳定度好于任何单颗脉冲星的频率稳定度，且综合脉冲星时6年以上频率稳定度优于1×10−15。不同算法结果比较表明，维纳滤波算法优于加权平均算法［46］。

2012年，Hobbs等［3］发表了利用Parkes脉冲星计时阵（Parkes Pulsar Timing Array，PPTA）19颗毫秒脉冲星约17年计时观测资料的综合脉冲星时研究结果。PPTA早期观测星数较少，且19颗星的观测数据分布非常不均匀，在2000年前后约1年多的时间内，甚至只有1颗星的数据可用。该研究结果采用基于TEMPO2软件的广义最小二乘拟合算法，得到采样间隔为1年（综合脉冲星时数据点间距为1年）的以TAI为参考的综合脉冲星时EPT（PPTA11）-TAI。请参见文献［3］。结果表明EPT（PPTA11）-TAI与已经消除线性及二次项的原子时TT（BIPM2011）-TAI具有类似的变化趋势，证明综合脉冲星时正确地揭示了TAI二阶以上的高阶系统误差。

应该指出的是，由于脉冲星自转参数拟合，计时观测参考原子时的线性及二次项误差被吸收到自转参数中了，脉冲星时只能探测原子时二次以上的高阶误差。为了方便脉冲星时与原子时的比较，本文中列出的原子时都是消除了二次多项式的原子时系统。

2019年Hobbs等［20］发表了利用国际脉冲星计时阵第一次释放数据研究得到的综合脉冲星时结果。利用IPTA 48颗毫秒脉冲星长期计时资料，采用基于TEMPO2软件的广义最小二乘拟合算法（作者团队又称之为“频率分析方法（Frequentist Analysis）”），得到的综合脉冲星时命名为TT（IPTA2016）。同时作者又从48颗毫秒脉冲星中筛选出8颗观测数据时间跨度较长，红噪声较小的毫秒脉冲星，采用贝叶斯算法构建了综合脉冲星时。因贝叶斯算法计算量非常大，耗时多，目前只能选用少数脉冲星构建综合脉冲星时。8颗星贝叶斯算法结果与48颗星广义最小二乘拟合算法结果在误差范围内相一致。作者团队同时给出了2种算法参考TAI的综合脉冲星时 TT（IPTA2016）-TAI和 参 考 TT（BIPM2017）的综合脉冲星时TT（IPTA2016）-TT（BIPM2017）。

图1重现了文献［20］由广义最小二乘拟合得到的综合脉冲星时TT（IPTA2016）-TAI及其误差棒，同时绘出了原子时TT（BIPM2017）-TAI，其中MJD表示修正儒略日。可见，综合脉冲星时TT（IPTA2016）-TAI与原子时TT（BIPM2017）-TAI变化趋势一致，表明综合脉冲星时TT（IPTA2016）-TAI基本上揭示了TAI的系统误差。从图1可看出，在MJD51000之前，综合脉冲星时TT（IPTA2016）-TAI与国际原子时TT（BIPM2017）-TAI偏离较大。主要是因为早期脉冲星计时TOA数量较少，且观测误差较大。作者给出的综合脉冲星时数据点1σ单边误差最大者达0.6 μs，最小约0.1 μs。综合脉冲星时数据点与国际原子时的偏离都在1σ误差范围内。另外，2种算法得到的以TT（BIPM2017）为参考的综合脉冲星时TT（IPTA2016）-TT（BIPM2017）具有相似的变化趋势，这或许在某种程度上反映了TT（BIPM2017）可能存在的系统误差［20］。通过太阳系行星历表误差对综合脉冲星时影响分析，Hoggs等［20］认为目前太阳系行星历表的误差可能是影响综合脉冲星时频率稳定度因素之一。

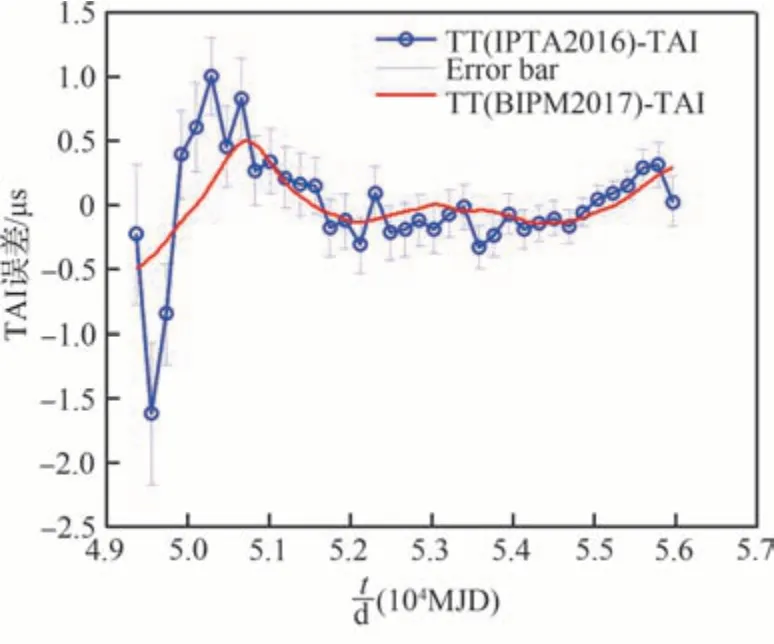
图1 综合脉冲星时TT（IPTA2016）-TAI与原子时TT（BIPM2017）-TAI比较［20］Fig.1 Comparison between ensemble pulsar time-scale TT（IPTA2016）-TAI and atomic time-scale TT（BIPM2017）-TAI［20］

最近，作者团队利用IPTA第二次释放的毫秒脉冲星计时观测资料［10］，采用改进的维纳滤波方法研究了综合脉冲星时。维纳滤波算法要求所有脉冲星观测数据覆盖相同时间跨度，并等间距采样。所以，作者团队选取了具有最长共同时间跨度（约16年），且中间TOA数据中断间隔小于400 d的10颗毫秒脉冲星。对传统维纳滤波算法的改进包括：

1）对计时残差的一次差进行傅里叶变换，然后再除以一次差分滤波器的转移函数［36］。试验证明这种方法比加平滑窗的傅里叶变换更能有效减小频谱泄露影响。

2）采用拟合得到的幂律模型功率谱计算自（互）协方差函数。

3）等间距采样的计时残差仍然包含较强的高频噪声，对计时残差进行适度平滑，消除高频噪声。

利用10颗星构建的参考TAI的综合脉冲星时EPT-TAI结果与误差棒绘于图2，图2还绘出了TT（BIPM2015）-TAI，可见EPT-TAI基本上反映了原子时TAI的系统误差TT（BIPM2015）-TAI。在图2中，综合脉冲星时1·σ单边误差最大者 为0.518 μs，最 小 为0.110 μs，平 均 为0.320 μs。综合脉冲星时误差与脉冲星计时TOA误差相关。进一步减小综合脉冲星时误差，有待于提高TOA测量精度与加密TOA采样数据点。在MJD53100附近，综合脉冲星时与原子时偏离较大，这与维纳滤波算法输入数据（拟合后计时残差）有关。很明显，综合脉冲星时所有数据点与原子时的偏离都在1·σ误差范围内。图1和图2是用2种不同算法得到的综合脉冲星时，采用的脉冲星数量与TOA时间跨度也不完全相同，但2种算法取得了类似的综合脉冲星时结果。采用同样方法，还计算了以TT（BIPM2015）为参考的综合脉冲星时EPT-TT（BIPM2015）。

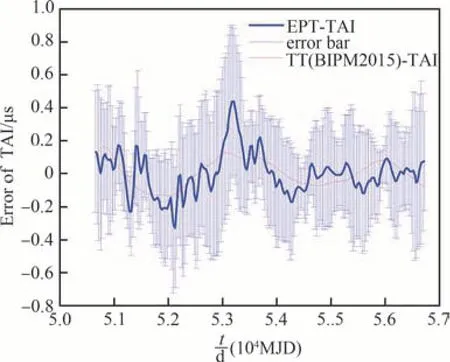
图2 综合脉冲星时EPT-TAI与原子时TT（BIPM2015）-TAI比较［10］Fig.2 Comparison between ensemble pulsar timescale EPT-TAI and atomic time-scale TT（BIPM2015）-TAI［10］

图3是综合脉冲星时EPT-TAI、EPT-TT（BIPM2015）、TT（IPTA2016）-TAI与 原 子 时TT（BIPM2015）-TAI频 率 稳 定 度（σZ［47］）的 比较。因为综合脉冲星时TT（IPTA2016）-TAI采样间隔较大（相邻采样点间隔为半年），共包含37个数据点（见图1），所以只能计算得到其4个σZ数据点。与傅里叶变换的功率谱分析相比，σZ更适合于低频红噪声的分析［47］。图3中，综合脉冲星 时EPT-TAI、EPT-TT（BIPM2015）在t=106.9s（等于90 d）的lgσZ值偏小，这是因为在计时残差数据预处理时采用了移动平均的缘故。从图3可看出，原子时TT（BIPM2015）-TAI的σZ曲线随时间增加，总体呈现上升趋势，说明原子时高频噪声较小，低频红噪声明显存在。而综合脉冲星时EPT-TAI、EPT-TT（BIPM2015）和TT（IPTA2016）-TAI的σZ曲线总体都呈现下降趋势，说明与原子时相反，综合脉冲星时存在明显的高频噪声，但看不出存在低频红噪声。综合脉冲星时在t=108.4s（约等于8年）及更长时间间隔的长期频率稳定度接近或略好于原子时TT（BIPM2015）-TAI。因此，脉冲星时与原子时具有互补作用，利用脉冲星时可以改进原子时的长期频率稳定度。脉冲星时长期频率稳定度优于与原子时，还有待于利用更多、更长时间序列资料进一步证明。由图1和图2也都能看出，原子时TT-TAI比构建的综合脉冲星时要平滑得多，表明原子时高频噪声比脉冲星时小，其短期频率稳定度优于脉冲星时（见图3）。

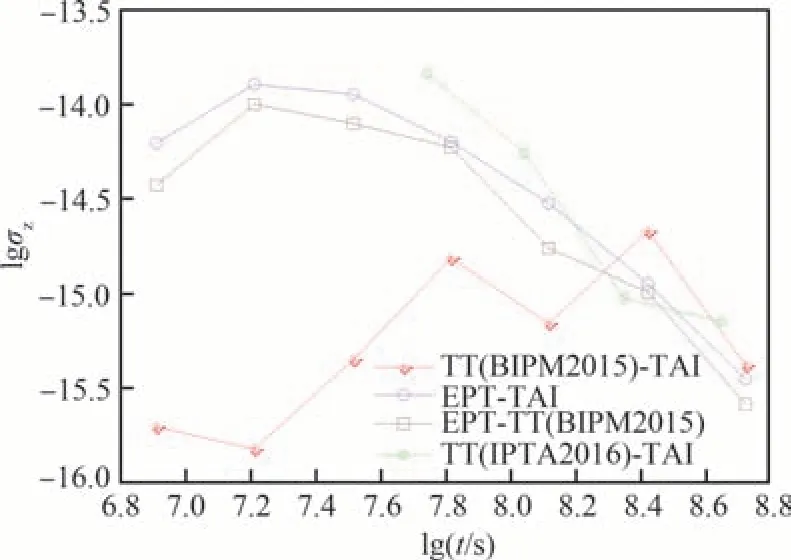
图3 综合脉冲星时EPT-TAI、EPT-TT（BIPM2015）、TT（IPTA2016）-TAI和原子时TT（BIPM2015）-TAI的频率稳定度［47］Fig.3 Frequency stability for ensemble pulsar timescales EPT-TAI， EPT-TT（BIPM2015）， TT（IPTA2016）-TAI and atomic time-scale TT（BIPM2015）-TAI［47］

有关用改进的维纳滤波算法构建综合脉冲星时的更详细描述，作者团队也在探索中。国际上和国内还有其他关于综合脉冲星时研究的结果，请见参考文献［48-49］。

4 总结与讨论

构建综合脉冲星时是从多颗脉冲星长期计时观测数据TOA中提取原子时系统误差信号的数据处理过程。只有在消除DM及其变化影响、正确估计每颗星的计时噪声、精确拟合每颗星计时模型参数情况下，才能利用合适算法提取出综合脉冲星时信号。目前，国际原子时TAI二阶以上的误差幅度小于0.2 μs，地球时TT的误差更小，而脉冲星计时观测平均精度为微秒量级。所以，综合脉冲星时算法是在具有微秒量级误差的TOA数据中，提取幅度小于0.2 μs的信号。脉冲星计时观测参考的太阳系行星历表误差，对计时残差影响与原子时误差影响量级上相近，来自宇宙的任何引力波可能是比原子时误差更弱的信号，目前，利用脉冲星计时只能给出随机背景引力波信号幅度的上限约束［50-51］。随着脉冲星计时观测时间长度增加，TOA观测精度不断提高，未来也许有可能采用更复杂的算法，同时探测原子时误差、太阳系历表误差与随机背景引力波信号［13］。

综合脉冲星时的广义最小二乘算法，需要将单颗脉冲星计时分析的广义最小二乘法推广到同时分析多颗脉冲星计时资料的情况，待拟合的参数除去每颗星计时模型参数外，再增加原子时误差模型参数。该方法输入数据包括每颗星的TOA序列数据、拟合后残差与每颗星计时模型参数近似估计值。利用每颗星计时模型参数的近似估计值，将计时模型线性化。由广义最小二乘法计算原子时误差模型参数与每颗星计时模型参数改正值，并同时计算所有参数的协方差矩阵。综合脉冲星时模型参数的最简单形式就是综合脉冲星时与原子时差值的直接采样。为得到精确的综合脉冲星时采样数据点，需要迭代运算。该方法的输出数据是等间隔采样的综合脉冲星时数据点、每颗星的计时模型参数及协方差矩阵。综合脉冲星时数据点采样间隔较大时，得到的综合脉冲星时较平滑，反之高频噪声较大。

综合脉冲星时贝叶斯算法，是将单颗脉冲星计时分析的贝叶斯方法推广到同时分析多颗脉冲星资料的情况，进而再增加综合脉冲星时模型参数，用贝叶斯方法同时分析得到综合脉冲星时参数、每颗星的计时模型参数与计时噪声模型参数。对于非线性计时模型的贝叶斯方法，其输入数据是每颗星的TOA序列数据与计时模型参数采用值。对于计时模型线性化的贝叶斯方法，输入数据还应包括每颗星拟合后残差。综合脉冲星时模型为幂律功率谱模型，其模型参数是谱指数与谱的幅度。贝叶斯方法的输出是每颗星的计时模型参数、计时噪声模型参数与综合脉冲星时模型参数。最后，由综合脉冲星时模型参数构建与综合脉冲星时信号有关的多颗脉冲星总计时残差的协方差矩阵；由每颗星的计时噪声模型参数和综合脉冲星时模型参数构建与计时噪声、综合脉冲星时信号有关的多颗星总计时残差协方差矩阵。再用这2个协方差矩阵按照式（29）构建综合脉冲星时波形，按照式（30）计算综合脉冲星时的协方差。最后得到的综合脉冲星时波形数据点分布与多颗星总计时残差数据点分布相同。受脉冲星计时白噪声影响，综合脉冲星时包含较大白噪声，进一步平滑处理是必要的。

与前二者不同，综合脉冲星时的维纳滤波算法首先是利用计时观测资料，分别对每颗脉冲星进行计时分析，获得每颗星拟合后计时残差，并对拟合后计时残差进行预处理，进一步得到等间隔采样的计时残差数据。并将此作为维纳滤波算法的输入数据。维纳滤波的特点是利用预处理后计时残差，计算每颗星残差的自协方差矩阵与不同脉冲星残差之间的互协方差矩阵，从而构建维纳滤波器。最后按照式（31）由每颗星等间隔采样的残差加权计算得到综合脉冲星时。维纳滤波算法输出数据就是综合脉冲星时采样数据点，其采样间隔与每颗星预处理后的残差间隔相同。由于脉冲星计时残差包含较大白噪声，为进一步削弱白噪声影响，还需要对维纳滤波得到的综合脉冲星时进行平滑处理。利用维纳滤波器与任何单颗星计时残差，还可以按照式（31）提取该单颗星的脉冲星时信号。综合脉冲星时误差由多颗星各自的脉冲星时信号加权平均的弥散度估计得到。

至今，所有已经发表的以TAI为参考的综合脉冲星时都能检测到TAI系统误差TT-TAI。文献［20］故意将TAI系统误差TT-TAI放大到2倍，得到假设的试验性时间尺度，用该试验时间尺度为参考构建的综合脉冲星时还能够检测到2倍的TT-TAI系统误差。利用同样的脉冲星计时观测资料，以地球时TT为参考构建的综合脉冲星时EPT-TT具有幅度更小的系统性变化。因为缺乏比TT更理想时间尺度作比较，EPTTT的误差主要来自于TT还是EPT，目前尚难确定。采用多种不同算法，利用不同计时观测资料构建EPT-TT，并进行互相比较，也许能够进一步揭示EPT-TT系统误差来源。以国际原子时TAI为参考构建的综合脉冲星时EPT-TAI是独立于TT-TAI的时间尺度，有可能作为地球时TT的另一个版本投入应用［3，20］。从未来的实际应用考虑，除去研究综合脉冲星时EPT-TAI构建方法（算法）外，还需要进一步研究综合脉冲星时的保持方法，即在构建EPT-TAI基础上，不断利用新的TOA观测资料延展并保持综合脉冲星时系统的问题。

目前，综合脉冲星时短期频率稳定度低于TAI，主要来自于较大的TOA测量误差。通过设计合适的滤波器，进一步滤除综合脉冲星时的高频分量，只保留需要的低频信号，可以改进综合脉冲星时的短期频率稳定度。虽然少数辐射信号较强、观测信噪比较高的毫秒脉冲星TOA测量精度最终会受到脉冲相位抖动的限制［52-53］，但对辐射信号较弱的大部分脉冲星，利用高灵敏度的设施能够不断提高TOA测量精度。例如中国FAST对毫秒脉冲星TOA的测量精度达到约0.05 μs，这将会明显改进未来综合脉冲星时的短期频率稳定度水平。综合脉冲星时的长期频率稳定度与地球时TT可比，甚至更好。随着脉冲星计时观测资料时间跨度增加，将会进一步验证综合脉冲星时长期稳定度水平。