基于仿脉冲星X射线信标的航天器定位方法

印俊秋，刘云鹏，2，汤晓斌，2，

1．南京航空航天大学 核科学与技术系，南京 210016 2．空间核技术应用与辐射防护工业和信息化部重点实验室，南京 210016

X射线脉冲星导航技术（X-ray Pulsar Navi⁃gation，XNAV）是一种具有发展潜力的新型空间自主导航技术。为了提高脉冲星导航定位精度，研究人员在脉冲星信号处理方法［1-2］、脉冲星数据库的建立［3］、导航算法［4-5］、导航误差分析［6］、高性能X射线探测器的研制［7］，以及与其他手段实现组合导航［8-9］等方面开展了大量的研究，并取得了一些积极的结果。XNAV本质上是一种信息传递的过程，脉冲星以固定的频率向航天器传递着特征波形信息，航天器将探测还原后的脉冲波形作为基本观测量对自身位置进行估计。脉冲星传递的X射线信号信噪比较低，影响了定位的实时性，因此导航信息更新慢、信号微弱探测难仍是目前制约X射线脉冲导航技术发展的最大障碍［10］。

受X射线脉冲星导航技术的启发，本文提出了一个新概念方案——基于X射线信标模仿脉冲星的航天器定位方法，即利用人造X射线信标模仿脉冲星发射高通量、高信噪比的特征脉冲信号，并将其编码在星历中；利用X射线探测器进行X射线的捕获分析，并与标准星历数据库中的数据进行对比，从而实现航天器的自主定位。这种航天器定位方法实质上是利用高质量的人造X射线源替代了脉冲星源发出X射线，将携带X射线源装置的信标卫星布置在行星层拉格朗日点等已知特定空间位置起到“脉冲星”的替代作用。此方案中设计使用X射线作为信标信号的载波，具有信号穿透能力强［11］、光束衍射极限低［12］、X射线源及探测器有小型化和集成化趋势［13-15］等优势。但该定位方案的可行性和其中不同因素对定位精度的影响尚待探究。

本文以火星探测转移段的航天器定位为例，系统研究X射线信标定位的实现过程和具体算法。考虑定位信标的寿命与轨道稳定性，选择行星层拉格朗日点布置信标卫星。航天器通过测量自身与信标卫星间的距离，基于三球交汇定位原理可实现对自身位置的估计。X射线信标作为定位基准，其自身轨道稳定性与辐射品质都会影响定位的精度，因此针对拉格朗日点卫星的自主导航方法进行简要描述，并基于优选脉冲星准则对辐射源参数进行初步优化。为研究X射线信标定位方法的具体性能，本文基于扩展卡尔曼滤波算法对航天器地火转移段进行仿真模拟，并对结果进行分析。

1 X射线信标定位方法

1.1 几何定位原理

X射线信标定位系统包括2部分：一是装载脉冲X射线辐射源的信标卫星，二是装有X射线探测器的航天器。信标卫星的实时轨道信息及播报信号特征都储存在航天器星载数据库中。脉冲X射线源通过调制X射线强度产生周期稳定的脉冲信号。由于X射线粒子性明显，辐射源出射的信号表现为离散的光子序列。在航天器运行中，探测器能实时接收来自视场内X射线信标的光子信号，在进行空间及物理效应的修正后按设定周期折叠还原可得航天器的脉冲到达时间（Time of Arrival，TOA）。同时提取星载数据库中信息推算出辐射源脉冲信号的发射时间，利用光速恒定的性质就可以计算航天器与信标卫星之间的距离。几何定位原理如图1所示。

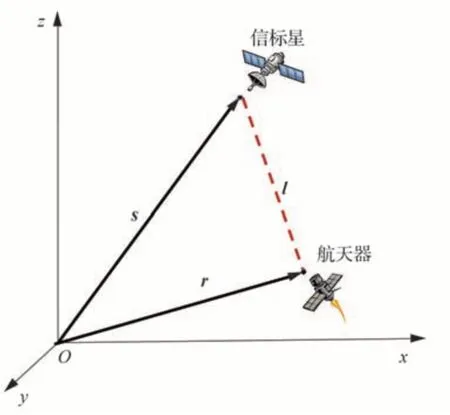
图1 X射线信标定位原理Fig. 1 Principle of X-ray beacon positioning system

以太阳中心为坐标原点，信标卫星的坐标矢量为s，其上发射某个脉冲的时间为t1。航天器的坐标矢量为r，探测到上述脉冲信号的时间为t2。信标到航天器的矢量为l，矢量l的模数值大小刚好对应着航天器与信标之间的距离值ρ，即

设光速为c，距离值可表示为

当同时观测3颗信标时，即可解算出航天器位置。

X射线信标定位方法的原理与X射线脉冲星导航类似，区别在于脉冲星距离太阳系非常遥远，X射线信号方向矢量看作常量并且无法准确获得航天器与脉冲星的距离，得出的导航观测量是航天器与太阳系内某一参考点（通常是太阳系质心SSB点）在脉冲星方向矢量上的投影长度。X射线信标作为太阳系内人造信标，航天器可以直接测量自身相对于信标的距离与方向矢量。

1.2 信标卫星位置的选取

对于深空导航，信标位置的选取是一个难题，需要综合考虑信标的覆盖范围以及中心天体引力与其他行星摄动力的综合影响。太阳系内，限制性三体力学是卫星运行的主要动力模型。对于这类问题，理论上可以解算出3个共线平衡解（Euler 特解）L1、L2、L3和2个等边三角形特解（Lagrange 特解）L4、L5，将这5个点称为拉格朗日点，也称为平动点。太阳系的拉格朗日点如图2所示。由于位于拉格朗日点的物体受到的引力加速度和向心加速度达到平衡，使得在拉格朗日点上部署的信标卫星可以处于受力平衡或亚平衡状态。卫星仅需消耗很少的能量就能进行轨道保持，增加了信标的寿命，还减小了信标网络的运营成本。因此，国内外研究者选取拉格朗日点放置卫星为各种深空探测器提供通信中继和导航的服务［16］。

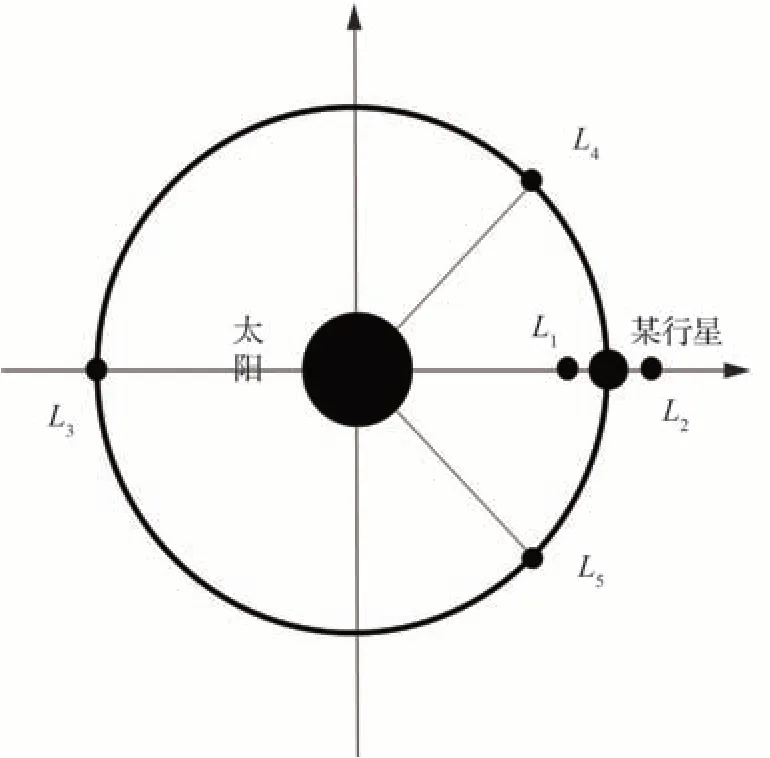
图2 太阳系中拉格朗日点的位置Fig. 2 Location of Lagrangian points in the solar system

拉格朗日点处的信标卫星实现深空航天器自主导航的前提是信标卫星能够保证自身轨道的稳定性。Hill［17］的研究表明，在第三体引力的强摄动影响下，拉格朗日点轨道处不具备强的旋转对称性，从而解决了地球附近卫星仅利用星间测距进行自主定轨时秩亏问题，因此可以仅利用星间测距实现拉格朗日轨道卫星的自主定轨；赵露华等［18］研究了X射线脉冲星导航方法应用于拉格朗日轨道卫星的自主导航；基于组合定轨方法，Yang等［19］进行了脉冲星与太阳的联合观测定轨研究，Gao等［20］进行了拉格朗日轨道导航星座与近地导航星座的长期自主定轨研究。

太阳系有八大行星，太阳与每颗行星都存在5个拉格朗日点。将太阳系八大行星轨道分为8个行星层，每一层都可以建立至少一组信标卫星网络。针对本文选取的航天器地火转移任务轨道，选择在地球层的拉格朗日点（简称日地系）和火星层的拉格朗日点（简称日火系）两组行星层发射信标卫星。但由于太阳质量太大，L3处卫星很多，而其对行星探测用处不大，所以在L3拉格朗日点处不设置信标。

2 数学模型

2.1 轨道动力学模型

以地火转移轨道为例，太阳引力为中心引力，在无轨道控制力作用时对航天器的运动起主要作用。在J2000.0日心黄道惯性坐标系上，建立航天器的轨道动力学方程［21］为

式中：r、v分别为航天器在日心黄道坐标系的位置矢量、速度矢量，且r=||r||；rpi为第i个摄动行星在日心黄道坐标系的位置矢量，且rpi=||rpi||；rri为第i个摄动行星相对于航天器的位置矢量，即rri=rpi−r，且rri=||rri||；μs为太阳引力常数；μi为第i个摄动行星的引力常数；np为摄动行星的个数；as为其他摄动力加速度矢量。本文对于地火转移轨道，考虑了太阳的中心引力以及地球与火星的引力摄动。

2.2 系统观测方程模型

在X射线信标定位系统中，信标的实时信号特征与轨道信息可由航天器内置的星载计算机精准计算并预报。当探测器捕获并恢复出信标的特征信号时，通过与星载数据库储存的信息进行相关对比，从而推算出航天器与信标间的距离形成导航的基本观测量。观测方程满足

式中：ρi（i=1，2，…，n）为第i颗信标与航天器间的距离；（xi， yi， zi）（i=1，2，…，n）为第i颗信标的坐标位置；（x， y， z）为航天器的坐标位置；η为观测噪声。

2.3 误差分析

X射线信标系统的定位精度主要依赖于系统观测方程模型的准确度，模型误差反映了模型与实际物理系统的偏差，即理论模型与实际情况越符合对于航天器位置的估计也就越精确。而轨道动力学模型的误差主要来源于计算中对于航天器所受摄动力的近似或取舍。实际上，滤波过程对于轨道动力学模型的误差并不敏感，而对脉冲到达时间观测量非常敏感。

在X射线信标定位方法中，不同信标组合的空间构型各有差异，对于航天器的位置估计效果也不同。X射线辐射源的稳定性和流量强度、观测时间、探测器的有效面积、探测器的时间分辨率、空间背景辐射都会对脉冲到达时间的测量造成影响，产生观测误差。信标卫星自主导航过程中也会存在误差，称为轨道误差，航天器与信标上装载的原子钟在没用校正的条件下也会发生单向漂移，称为时钟误差。因此，本文重点分析航天器的观测误差、观测信标的个数、信标的空间构型、信标网络的稳定性等对航天器定位性能的影响。

3 X射线辐射源

3.1 可行性分析

脉冲星属于高速旋转的中子星，稳定的自转周期与辐射特性使以接收到的脉冲星信号为基准对航天器进行导航定位成为可能。不同脉冲星产生的脉冲X射线周期与波形均不同，并且信号频率越高、脉冲宽度越窄，航天器定位精度越高［22］。因此，本文方案中人造辐射源的时间分辨率对提升航天器的定位精度尤为重要。以目前工艺成熟、易小型化的X射线管体制为例进行辐射源时间特性分析。

X射线管阴极产生的电子经过高压电场加速轰击阳极靶材，进而产生X射线。因此，X射线管辐射源的时间特性与电子产生及打靶的物理过程紧密相关。Hang等［23］对光控X射线管时间特性进行模拟研究，考虑光阴极外光电效应和微通道板电子倍增效应，计算得到最短调制脉冲为59 ps。日本滨松公司已开发出光阴极X射线管产品，可实现小于100 ps的超短脉冲发射［24］。Feng等［25］对热阴极栅控X射线管中电子运动进行模拟研究，计算得到电子弛豫时间小于10 ns，并且在后续实验中实现了5 MHz的重频脉冲发射，远超脉冲星导航中应用的毫秒脉冲星的自转频率。

X射线可以在真空中无衰减地传输，但实际的辐射源存在着一定的发散角，导致接收端的光子流量随距离的增加而减小。为探究辐射源的实际应用需求，建立如图3所示简化X射线信号传输模型。图3中，D为辐射源发射孔直径，θ为X射线经过准直后的发散角，L为X射线信号的传输距离。若辐射源的发射功率为Pt，探测器单位面积的接收功率为Pr，两者关系公式为

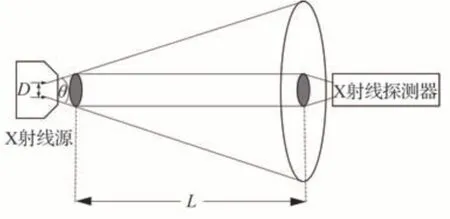
图3 X射线信号传输模型Fig. 3 X-ray signal transmission model

本文针对地火转移任务场景，考虑地火最远距离4×108km，假设辐射源发射孔直径为0.05 mm，光子能量为10 keV，使接收端光子流量达到蟹状星云脉冲星水平，分析辐射源所需要的发射功率与发散角。

由图4结果可知，若要保证接收端光子流量达到蟹状星云脉冲星水平，辐射源发射功率在100 W内，辐射源发散角需要收敛到μrad量级。为获得小发散角X射线光束，需要将辐射源匹配准直X射线光束的方法和光学器件使用。国内外科研工作者采用定向晶体、多层膜反射镜、毛细管X射线等光学器件［26］，获得了实验室光束发散度小的X射线源。Bernhardt等［27］在欧洲同步辐射光源上进行实验，使用单晶金刚石Channelcut型单色器将能量为9881.1 eV的X射线发散角收敛到6.1 μrad（定义中心亮度1/2处为光斑边缘）。Wang等［28］针对X射线空间传输设计准直光学，采用基于旋转圆锥面的结构对光束进行收敛，考虑韧致辐射X射线源的实际发散角，钨靶X射线能谱，W/SiO2薄膜实际粗糙度0.3 nm，计算得到光束发散角为2 μrad（定义中心亮度1/e处为光斑边缘）。

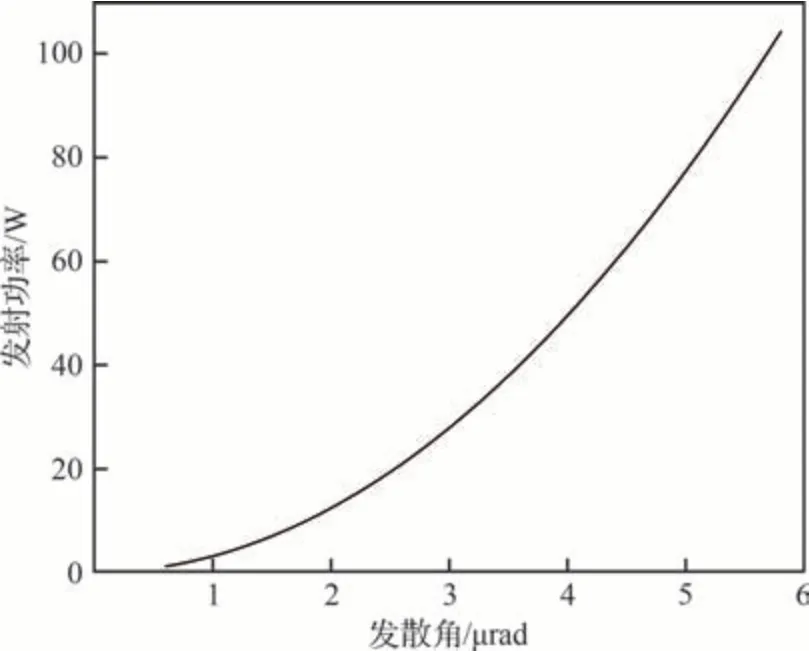
图4 辐射源不同发散角所需功率Fig. 4 Power required for different divergence angles

3.2 参数优化

在X射线脉冲星导航技术中，为保证航天器定位的有效性与精度，需要对航天器观测的脉冲星进行筛选，因此提出了优选脉冲星准则。优选脉冲星准则包括对脉冲星的可见性因素、品质因素、空间分布因素的分析，在X射线信标定位系统中依然适用。鉴于本文方案已选定拉格朗日点放置信标，所以着重对辐射源的品质因素进行优化。准则中通常使用品质因子Qx［22］评价射线源信号质量

式中：Fx为脉冲星辐射的射线光子流量；pf为脉冲流量比；P为脉冲周期；W为脉冲宽度。由式（6）可得，辐射源光子流量越大，背景辐射越小，信号频率越高，脉冲宽度越窄，该辐射源品质因子越大，定位精度越高。

航天器的定位精度主要受观测量影响，观测的测量精度与辐射源参数、探测器性能直接相关。脉冲到达时间的测量精度σTOA计算公式［29］为

式中：Tb为探测器的时间分辨率；tm为总的观测时间；λp为脉冲信号平均流量密度；λn为空间背景噪声的平均流量密度；A为探测器敏感面积；T50为射线脉冲信号半流量密度持续时间，该参数与脉冲信号的周期、轮廓有关。若给定探测器敏感面积A=1 m2，时间分辨率为1 μs；观测时间长度为300 s；空间背景噪声的平均流量密度为λn=50 photons/（m2·s）。可调整脉冲辐射源的信号辐射流量、脉冲轮廓特征以减小观测量的误差，进而提升定位精度。但在实际中，辐射源功率和带宽不能无限提升，探测器的时间分辨率也限制着波形的恢复精度。因此，下面基于现有脉冲星对辐射源参数进行初步优化。

在上述给定条件下，分别计算脉冲星PSR B1937+21、PSR B0531+21的TOA测量精度，其中PSR B0531+21蟹状星云脉冲星光子流量很强，PSR B1937+21脉冲星信号微弱但脉冲轮廓较好。X射线辐射源可通过调节发射功率和脉冲宽度实现波形及周期各异的脉冲X射线发射。设计辐射源适当减小脉冲宽度及周期，并在接收端将光子流量提升到与蟹状星云脉冲星相当。不同辐射源的TOA测量误差如表1所示。

表1 不同辐射源的TOA测量误差Table 1 TOA measurement errors for different radia‑tion sources

利用人造辐射源综合两颗脉冲星的优势特征，使得TOA测量精度大幅提升。优化后的人造脉冲辐射源50 ns的TOA测量误差对应的观测误差为15 m。

4 仿真验证及结果分析

4.1 仿真场景建模

为了验证信标定位方法的可行性及性能，以火星探测任务为背景，以实现地火转移轨道航天器自主定位为目标进行仿真。利用STK（Satel⁃lite Tool Kit）软件轨道机动模块Astrogator来设计航天器的任务轨道，航天器轨道参数如表2所示。

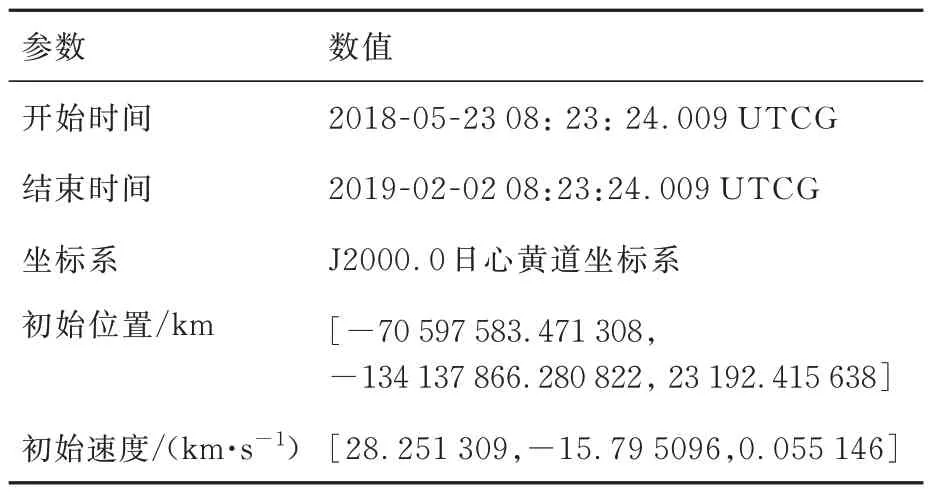
表2 地火转移轨道参数Table 2 Parameters of Earth-Mars transfer trajectory

建立日地系拉格朗日点对应4颗信标卫星 SE1、SE2、SE4、SE5的轨道，同样的，对于日火系拉格朗日点也建立了4颗信标卫星SM1、SM2、SM4、SM5，其中SE4和SM1卫星的轨道模型如图5所示。为了简化计算，本模型中不涉及多普勒频移。

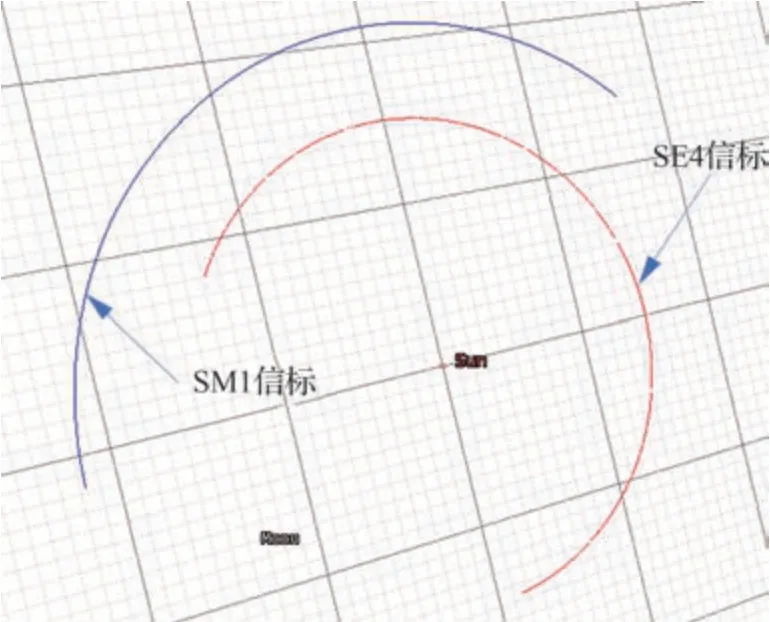
图5 日地系信标卫星SE4、SM1的3D示意图Fig. 5 3D schematic diagram of the Sun-Mars beacon satellite

4.2 可见性分析

由于地球等其他天体的自转和公转运动，航天器与信标卫星间可能会存在遮挡，当航天器与信标卫星可见时，直接的信号传输链路才能建立起来。分析信标卫星对于航天器的可见性是对航天器进行导航精度分析之前的必要步骤。

从STK软件建立的地火转移场景中得到信标相对于航天器的可见性分析如图6所示，整个仿真周期157 d内，航天器对于场景中建立的信标具有全程可见性。对于航天器的地火转移轨道场景，设置在日地系、日火系拉格朗日点的信标不仅受力稳定，而且还拥有星间遮挡少的优势。

图6 航天器对信标可见性结果Fig. 6 Visibility of spacecraft to beacons

4.3 扩展卡尔曼滤波算法

由于状态方程和观测方程一般存在着噪声，为了获取高精度的定位结果，就需要用合适的滤波方法对航天器的状态信息进行实时估算。Kal⁃man滤波器是解决线性估计问题的利器。然而，在深空探测器自主定位的过程中，观测模型和轨道动力学模型是非线性的，为了解决导航系统中的非线性问题，就出现了针对一般非线性问题的扩展卡尔曼滤波（Extended Kalman Filter，EKF），EKF的基本原理是将当前非线性系统方程在状态估值处以泰勒级数展开，保留一阶项、舍去高阶项按线性方程进行处理。

基于第3节辐射源初步优化结果，设计辐射源参数使TOA测量精度为50 ns，其他参数不变。表3给出了轨道的初始误差。

表3 轨道初始误差设置Table 3 Initial orbital error

仿真开始时间为 201808-1004：00：00.000 UTCG（Universal Time Coordinated Grego⁃rian），仿真时间为1 d。对于日地系、日火系共8颗X射线信标，同时观测3颗信标时存在56种组合方式，对每一种情况依次仿真并待滤波收敛后记录下航天器位置、速度的均方根误差。

4.4 信标几何分布的影响

放置在不同拉格朗日点的信标相互组合、协同工作，构成了一个庞大的信标定位网络。由于各个信标位置的不同，所组成的定位体系的空间构型也有所差异，为了探究不同空间构型对于定位性能的影响，分析56种信标组合的仿真结果发现如下规律：

1）1 d仿真时间内，同时观测3颗信标的56种组合滤波结果均收敛。共有31组误差在1 km内，其中22组误差在200 m以内；有20组误差处于1～5 km区间内；剩余5组定位误差均在5 km以上。定位精度最高的是SE2-SM1-SM5组合，误差为152 m；定位精度最低的是SE1-SE4-SM5组合，误差为14.96 km。

2）L1、L2拉格朗日点信标与其他信标的组合误差总是偏大的；观测组合中SE1、SE2或SM1、SM2互换对定位精度影响很小。

从信标的空间分布上对结果作简要分析，2018-05-2304：00：00.000 UTCG时刻日火系信标相对距离如表4所示，L1、L2拉格朗日点信标间的距离远小于其他信标之间的距离。从卫星仿真工具包（Satellite Tool Kit，STK）软件场景图（见图7）中也能观察到日地系与日火系的L1、L2拉格朗日点信标分别分布在地球与火星的轨道两侧，两者之间的相对距离对于地火转移轨道的尺度来说是比较小的，所以L1、L2点信标组合空间构型较差，定位精度较低。对于大尺度空间下的航天器定位，观测L1、L2点处的信标定位效果相当，但这两点处于行星轨道两侧，协同互补有覆盖整个宇宙空间的潜力。

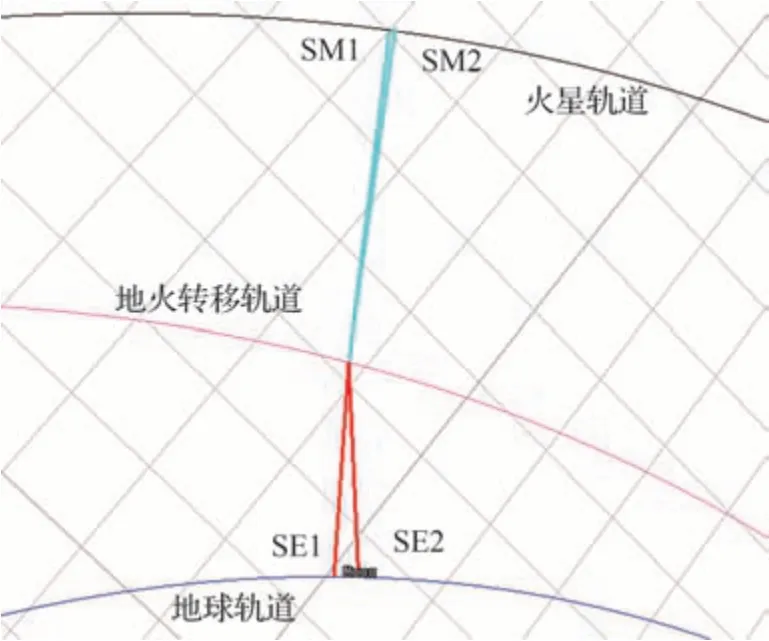
图7 STK3D场景中航天器与两系L1、L2点处信标的位置关系Fig. 7 Position relationship between spacecraft and the two series L1 and L2 points in the STK 3D scenario

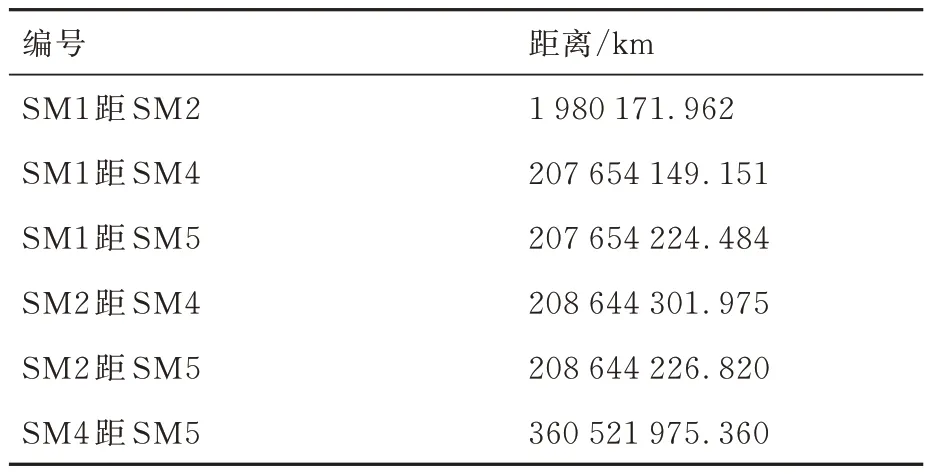
表4 信标间的距离Table 4 Distance between beacons

为了在实际空间任务中实时规划最优的导航信标组合，需要建立统一的评价标准对于不同的信标网络进行筛选。结合脉冲星导航、GPS导航系统选星方法经验，引入几何精度因子（Geo⁃metric Dilution of Precision，GDOP）表征不同信标空间构型对定位精度的影响

式中：H为一阶线性化后的观测矩阵。

如果GDOP越小，则估计精度越高，反之越低。分别计算56种信标组合的GDOP数值，可以发现GDOP与航天器位置估计误差相互对应。表5给出各误差区间若干信标组合的定位精度及对应的几何精度因子。

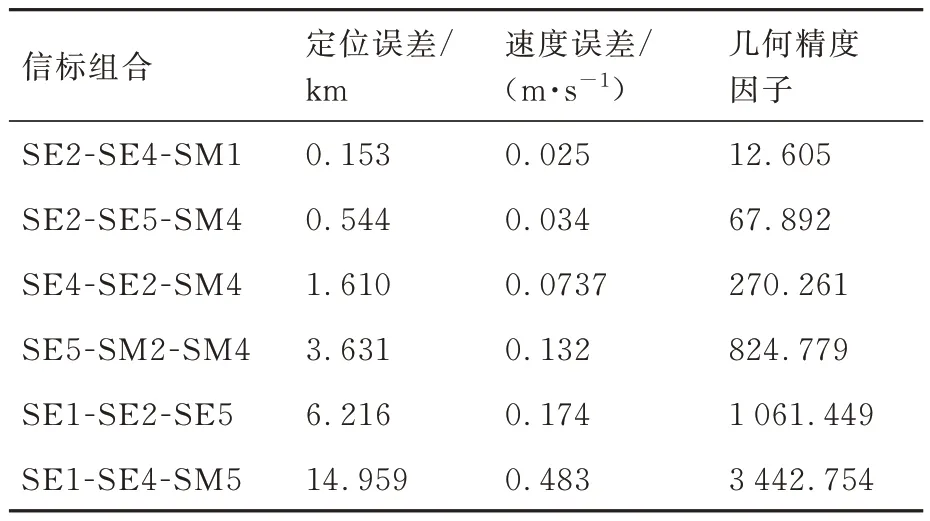
表5 部分组合定位误差与几何精度因子Table 5 Positioning error and GDOP for some groups

航天器的定位精度受信标的空间分布影响较大，定位过程中实时规划选取合适的信标组合非常关键。由于宇宙中拉格朗日点非常有限，可设置的信标数量较少，导致航天器运行期间可供选择的信标组合比较单一。信标设置在围绕太阳公转的行星轨道上，这些行星轨道的倾角都比较小，从大尺度上可以近似看作一个平面，本文的任务背景是地火转移轨道，这种空间构型阻碍了航天器定位精度的进一步提升。

4.5 观测误差的影响

X射线信标定位系统的基本原理是基于航天器与信标间的距离测量，距离测量的误差大小直接影响了航天器的定位精度。辐射源的光子流量、波形特征，探测器的面积、时间分辨率以及空间背景辐射都会对测量结果产生影响。为探究不同程度的观测误差对航天器定位性能的影响，假设TOA测量精度分别为50 ns、500 ns、5 μs、50 μs，选取GDOP值最优的SE2-SM1-SM5信标组合在对应的观测误差下进行仿真。表6、图8分别表示不同观测误差对应的定位精度以及滤波收敛过程。

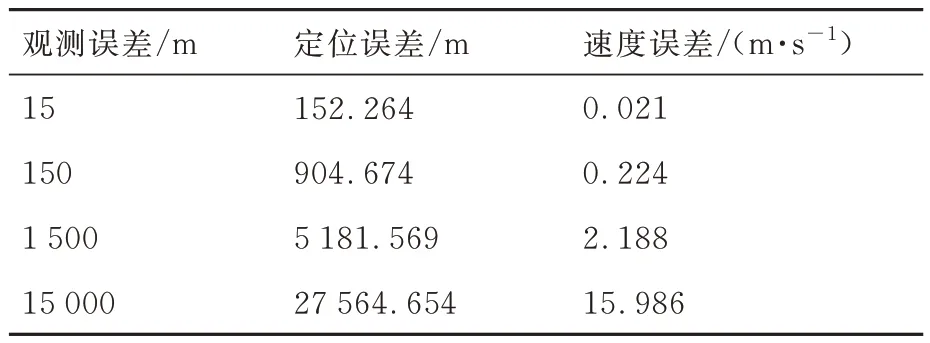
表6 观测误差对应的状态估计精度Table 6 State estimation accuracy corresponding to observation error

表8数据显示，随着观测误差的增大，航天器位置、速度的估计精度不断降低。从图8同样可以直观地看到观测误差对于定位精度的影响趋势，并且还可以注意到随着观测误差的不断增大，滤波的收敛时间也不断增加。为保证X射线信标导航系统的工程应用，可通过优化辐射源参数、研发高性能X射线探测器等措施减小观测误差。

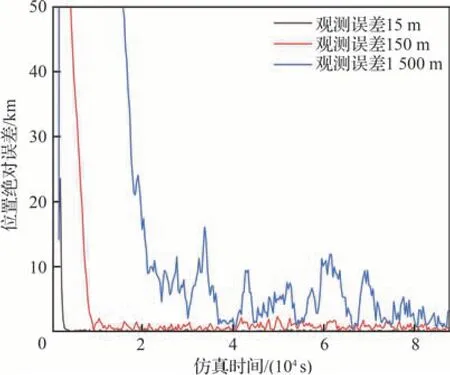
图8 观测误差对滤波性能的影响Fig. 8 Influence of observation error on filtering performance

4.6 信标数量的影响

由4.2节可见性分析，航天器在地火转移场景中始终对信标拥有良好的可见性，所以存在航天器同时观测多颗信标的情况。为探究航天器观测不同数量信标时的定位性能，分别选取GDOP较差的SM1-SM2-SE2信标组合和GDOP较好的SE4-SE5-SM4信标组合，随机增加或减少观测的信标数量进行仿真，记录下组合改变后的定位误差、速度误差以及对应的GDOP。表7、图9表示基于SM1-SM2-SE2组合改变信标数量的仿真结果。表8、图10所示为基于SE4-SE5-SM4组合改变信标数量的仿真q结果。

表7 SM1‑SM2‑SE2组合改变信标数量对应的状态估计精度Table 7 State estimation accuracy of changing number of beacons based on combination of SM1‑SM2‑SE2

图9 SM1-SM2-SE2组合改变信标数量对滤波性能的影响Fig. 9 Effect of changing number of beacons on filter⁃ing performance based on combination of SM1-SM2-SE2

图10 SE4-SE5-SM4组合改变信标数量对滤波性能的影响Fig. 10 Effect of changing number of beacons on filter⁃ing performance based on combination of SE4-SE5-SM4

仿真结果表明，仅通过距离测量，单信标及双信标的组合均无法对航天器的位置进行有效估计。通过增加观测的信标数量，滤波结果开始收敛，并且随着观测信标数量的增加，航天器对于自身位置的估计精度也不断提升，同时GDOP值的变化也能反映出此规律。增加观测的信标数量对原先定位误差较大的信标组合提升明显，如表7；对于原先定位精度较好的组合提升十分有限，如表8。因此航天器定位时，首先要基于GDOP筛选出最优的观测信标组合，根据需求合理选取观测信标的数量，不能一味地增加观测量，这对降低航天器功耗、优化资源配置具有重要意义。

表8 SE4‑SE5‑SM4组合改变信标数量对应的状态估计精度Table 8 State estimation accuracy of changing number of beacons based on combination of SE4‑SE5‑SM4

4.7 轨道误差与钟差的影响

X射线信标定位方法是一种相对定位方法，信标卫星的轨道稳定性影响着航天器的定位效果。位于拉格朗日点的信标卫星依靠自主导航方法对自身的轨道进行保持，但由于实际空间受力环境的复杂性，势必会造成实际位置与理论位置的偏移，称为轨道误差。为了探究位置偏移程度对于信标定位性能的影响，令信标轨道误差在0～1000 km变化，选取SE2-SM5-SM1信标组合进行仿真，结果如表9、图11所示。

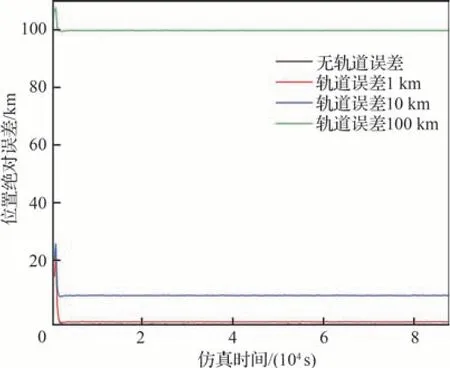
图11 轨道误差对滤波性能的影响Fig. 11 Influence of orbital error on filtering performance

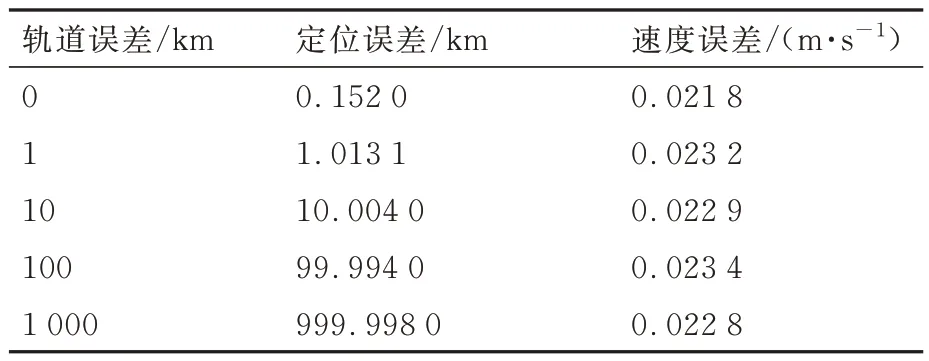
表9 轨道误差对应的状态估计精度Table 9 State estimation accuracy corresponding to or‑bital error

假设航天器与信标卫星上分别装载有铯原子钟。已知其振动频率为9192631770 Hz，当其测量1 s时误差为一个周期的误差。航天器共历时6809796 s，对应钟差为7.4×10−4s。信标运行1、5 a所产生 的钟差分别为3.43×10−3、1.71×10−2s。选取SE2-SE4-SM1组合在不同的钟差下进行仿真，结果如表10所示。

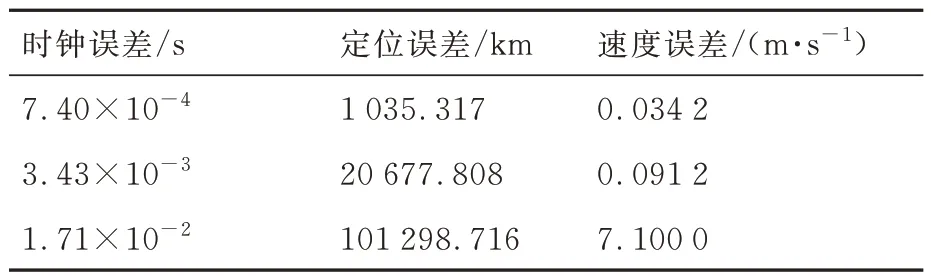
表10 钟差对应的状态估计精度Table 10 State estimation accuracy corresponding to clock errors

从仿真结果可以看出，随着钟差与轨道误差的不断增大，航天器的定位精度在不断下降，甚至会到达失效的程度。轨道误差与钟差同属于系统误差，卡尔曼滤波算法可以对定位过程中的随机误差进行滤除，但无法对系统误差进行有效的修正，所以轨道误差与时钟误差对于航天器的定位精度影响较大。

5 结论

受X射线脉冲星导航技术的启发，提出了一个新概念方案，即利用X射线信标模仿脉冲星发送高质量脉冲信号的航天器定位方法，并以地火转移轨道航天器自主导航为背景开展了初步仿真研究。仿真结果初步验证了方案的可行性，研究结果表明，设置在太阳系行星层拉格朗日点的信标运行稳定，覆盖范围广；本方案中设置的信标可以很好地为太阳系内的航天器提供定位服务，在同时观测3颗及以上信标，TOA测量精度为50 ns的条件下，大部分信标的组合都能将定位误差控制在1 km以内。此外，本方案中的X射线探测与信号恢复方法与脉冲星导航相似，可共用一套光学与探测设备，无需进行新模块的研发。航天器运行中，可进行信标信号与脉冲星信号的同时接收，进一步提升定位系统的定位精度与故障冗余度。

虽然此X射线信标定位方案的实现还面临着许多挑战，比如常规的栅控X射线管存在产生X射线的能量转换效率较低，光束发散角较大，需要使用高压电源等问题，就目前本方案的工程实现可能还存在相当的困难。但随着微焦斑X射线源［30］的迅速发展，X射线管光源的发散角及系统功耗可进一步减小；台面化激光等离子体X射线源［31］拥有更高的能量转化效率、更小的发散角，可能也是一个未来具有应用潜力的解决方案；本研究团队已开发的栅控X射线管频率可达5 MHz［25］，远超脉冲星导航中应用的毫秒脉冲星的自转频率，为本方案中的航天器定位精度和实时性的进一步提升打下了坚实的技术基础。因此，随着以上X射线源技术的不断发展，辐射源的功耗和发散角等参数可得到进一步优化，使本方案的工程实现成为可能。