利用Crab脉冲星X射线观测校准星载原子钟频率

童明雷，韩孟纳，杨廷高，赵成仕，朱幸芝

1．中国科学院 国家授时中心，西安 710600 2．中国科学院大学，北京 100049

脉冲星是大质量恒星超新星爆发或双星吸积塌缩后形成的带强磁场的中子星，其旋转产生的辐射束可被地面射电望远镜或空间高能探测器接收。因其超高温、超高压、超高密度、超强磁场、超强电场、超强引力场等极端物理条件，脉冲星成为天文和物理研究的天然实验室。脉冲星是20世纪60年代的四大天文发现之一。脉冲星的观测和理论研究自发现以来已持续了50多年，是天体物理领域重要的研究对象。

国内外对脉冲星的射电观测已长达数十年之久，随着各种地面大型射电望远镜的陆续建成，天文学家对脉冲星的形成、辐射机制、内部结构及旋转特征等进行了深入研究［1］。值得一提的是，2020年12月1日，因馈源平台坠落导致受损严重的阿雷西博射电望远镜（Arecibo）在其服役期间对脉冲星的观测取得了众多划时代成果［2］：1974年Hulst和Taylor发现了第1个脉冲星-中子星双星系统（PSR B1913+16），间接证明了引力波的存在［3］；1982年发现了第1颗毫秒脉冲星（PSR B1937+21）［4］；1992年Wolszczan和Frail发现第1颗伴星为行星的脉冲星（PSR B1257+12）［5］，这是人类首次发现系外行星。随着Are⁃cibo的落幕，被誉为“中国天眼”的500 m口径球面射电望远镜（FAST）于2021年3月31日对全球开放，接受来自全世界的观测申请。国际上，中国参与了平方公里阵（SKA）项目，并将脉冲星搜寻、脉冲星测时及引力检验作为重点研究方向之一。

深空探测任务具有距离远、延迟长、信号弱等特点，在此条件下高精度导航始终是深空测控技术需要重点解决的问题。X射线脉冲星导航作为一种新的天文导航方式，通过观测脉冲星辐射的X射线光子，便可获得高精度的测距信息与时间信息［6］。脉冲星辐射的高能X射线集中了绝大部分的辐射能量，易于被小型化探测器接收，有利于减小航天器有效载荷的尺寸。同时，脉冲星导航弥补了全球卫星导航系统（GNSS）导航精度随测控距离的增加而降低的缺陷，是一种真正意义上的自主导航，适用于广阔的太阳系空间的深空探测甚至星际飞行任务的航天器自主导航，近年来逐渐成为国内外研究的热点。

脉冲星导航虽然未来应用前景广泛，但由于X射线探测器的灵敏度较低，探测流量极低的毫秒脉冲星还比较困难，因此目前并没有实质的应用。而利用脉冲星进行空间自主守时有望更早地获得应用。由于脉冲星时的长期稳定性好，基于射电波段的长期脉冲星计时观测资料可以建立脉冲星时［7-8］。有些观测精度较高的脉冲星，利用其2～3年计时数据就可以建立稳定脉冲星时［9］。对于既有射电辐射又有X射线辐射的脉冲星，在利用射电波段构建脉冲星计时模型参数后可以作为数据库，联合X射线波段的计时观测用于空间守时系统。由于脉冲星的自转频率变化率通常很小，因此短时间内脉冲星的自转频率非常稳定，构成一种频率基准，基于此可以校准原子钟的频率，提高其准确度。本文将结合Crab脉冲星射电波段数据库和X射线计时观测进行空间自主守时研究，利用脉冲星改正空间原子钟的频率偏差而不依赖于地面。

脉冲星导航试验卫星（XPNAV-1）是由中国航天科技集团第五研究院研制的中国首颗X射线脉冲星导航试验卫星，于北京时间2016年11月10日在酒泉卫星发射中心由长征11号运载火箭发射升空［10］。卫星轨道高度500 km，轨道周期94 min。因在执行观测任务时为降低对探测器的损害，卫星在观测时避开了南大西洋异常区，每个观测弧段的持续时间通常只有30～50 min［11-12］。卫星采用整星零动量三轴稳定姿态控制方式，搭载了掠入射Wolter-I聚焦型探测器和准直型微通道板探测器［13］。Crab脉冲星（PSR B0531+21）作为天空中最明亮的X射线源之一，成为XPNAV-1卫星进行在轨标定的标准源。本文主要对XPNAV-1卫星的Crab脉冲星观测数据进行处理，分析研究了星载原子钟的频率偏差对脉冲到达时间的影响，据此进一步给出可对频率偏差进行修正的方法。

1 X射线脉冲星计时

与射电脉冲星计时不同，X射线探测器记录的是X射线光子的到达时刻。XPNAV-1卫星的公开发布数据［14］包括光子事件文件和轨道文件2类数据。由于光子到达探测器的时刻与卫星轨道遥测时刻并不一致，因此需要在光子到达时刻内插出航天器的位置与速度。卫星在绕地飞行时，其所处的引力场是在不断变化的，“多普勒效应”“引力红移”以及视差等效应会使探测器探测到的光子到达时刻失去周期性，需将光子到达探测器的时刻转换为到达太阳系质心（SSB）的时刻。到达时间的转换模型包括：卫星绕地运动和地球公转引起的几何延迟、引力场中光线弯曲引起的Shap⁃iro延迟、引力场中时间尺度变换的Einstein延迟等，具体过程可见文献［15-16］中的描述。

1.1 脉冲轮廓折叠

要得到脉冲到达SSB的时刻（TOA），需要将光子到达SSB的时间序列先进行历元折叠得到积分脉冲轮廓与标准脉冲轮廓，再由二者的相关获得脉冲到达时间。历元折叠方法是将脉冲星的自转周期均匀划分为N等份（bin数），统计落入每个bin的光子数，从而获得脉冲轮廓。折叠过程使用Jodrell Bank天文台射电观测的Crab脉冲星自转模型参数［17］，使用的2段Crab脉冲星自转参数如表1所示。在公开发布数据时间跨度内，Crab脉冲星自转参数更新过一次。表1中P1代表第1段自转参数，P2代表第2段自转参数。当光子到达时刻（以约化儒略日表示）<57727时，使用P1，否则使用P2。

表1 Crab脉冲星自转参数Table 1 Spin parameters of Crab pulsar

在进行脉冲轮廓折叠时，若子相位间隔数N取值太大，则折叠的脉冲轮廓会损失信噪比；若N取值太小，脉冲轮廓将过于平滑，丢失频域信息。图1给出了采用第24组数据、按不同N（分别取64、128、256、512、1024、4096）折叠的积分脉冲轮廓，显然脉冲轮廓的信噪比明显地依赖于N值的选取。表2给出了各脉冲轮廓的信噪比（SNR），计算公式［18］为

图1 积分脉冲轮廓随子相位间隔数的变化Fig. 1 Variations of integrated pulse profile with number of sub-phase intervals

式中：Npeak为脉冲轮廓主峰的光子数；Ntotal为观测的总光子数；p为曝光时间。表2中p均为44735 s。此外，N的取值也与探测器的灵敏度以及每个观测文件的数据量有关。脉冲星轮廓的SNR只是作计时数据处理的一个参考，不能作为唯一标准。尽管表2中N=64的信噪比最高，但其脉冲星轮廓的形状可能已经失真。后面的分析发现N取［64，512］的范围内，计时结果很稳定。因此如无特别说明，不失一般性地均取N=256［19］。

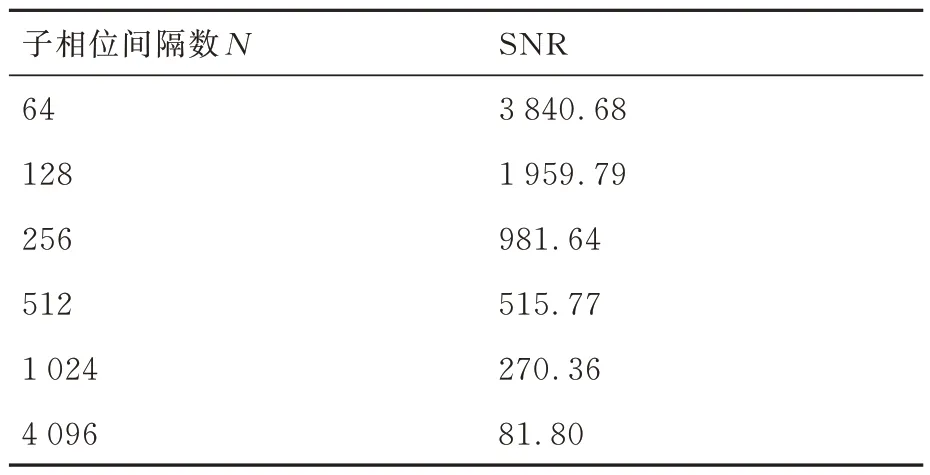
表2 按不同子相位间隔数折叠的积分脉冲轮廓SNRTable 2 Signal-to-noise ratio of integrated pulse profile folded by different number of sub-phase intervals

Jodrell Bank天文台发布的Crab脉冲星星历参数是基于美国JPL太阳系行星历表DE200得到的，而JPL历表参考的时间尺度是太阳系质心力学时（TDB），因此表1中t0给出的是TDB时刻。折叠的标准脉冲轮廓如图2所示。

图2 标准脉冲轮廓Fig. 2 Standard pulse profile

1.2 脉冲轮廓平滑

当脉冲轮廓折叠所用的光子数过少时，得到的脉冲轮廓信噪比会很低，从而影响脉冲到达时间的确定，通常需将轮廓进行平滑降噪处理。核回归作为一种非参数估计方法，其对数据的分布特征不附加任何假定，是一种从数据本身出发研究数据分布特征的方法［20］。定义x处的观测量为

式中：yi为x处的已知观测量；wi(x)为x处的权函数。权函数的定义为

其中：h为核宽度，h的大小决定了平滑程度；κ(m)为核函数。本文比较了3种常用的核平滑方法（Gaussian核平滑、Epanech⁃nikov核平滑以及Tri-cube核平滑）对脉冲轮廓的平滑效果。3种核函数的定义为

式中，κ1(m)、κ2(m)、κ3(m)分别为Gaussian核函数、Epanechnikov核函数以及Tri-cube核函数。

平滑的具体方法是选取其中一组原始积分脉冲轮廓，采用上述3种方法进行降噪处理，处理后的结果如图3所示。可以发现，当使用相同的核宽度时，相较于其他2种核回归法，Gaussian核回归可以有效去除脉冲轮廓中的随机噪声并保留信号的峰值特征，平滑效果最好。且由于高斯核函数灵活性比较高，当特征数较小时，一般采用高斯核回归平滑含噪声的信号。因此下文均采用Gaussian核回归平滑法对脉冲轮廓降噪处理。

图3 脉冲轮廓经3种核回归处理前后的结果比较Fig. 3 Results of pulse profile before and after being processed by three kernel regressions

1.3 计时残差获取

计时残差是衡量脉冲星计时水平的一个重要因素，要得到计时残差需要首先获得TOA数据。本文的TOA是采用积分脉冲轮廓与标准脉冲轮廓经DFT之后在频域互相关［21］的方法得到的，频域互相关相较于时域互相关可以获得更高的TOA测量精度。计时残差为测量的TOA与模型预报的TOA之差［22］，即

式中：R(t)表示计时残差；ϕ(t)为脉冲到达时刻t对应的相位，N(t)为与ϕ(t)最接近的整数，ν为所观测脉冲星的自转频率。

将XPNAV-1卫星的35组观测数据，结合Jodrell Bank发布的Crab脉冲星的射电计时模型参数，并拟合掉2个波段的零点相位差后得到的拟合前计时残差如图4所示，图中脉冲到达时刻用约化儒略日（MJD）表示。零点相位差不存在长期变化趋势，在短时间内变化很小，可近似视为常数［23-24］。图4的结果利用了全部数据构建的标准脉冲星轮廓，得到的计时残差均方根（RMS）值为29.4853 μs。在这35组观测数据的时间跨度内，Crab脉冲星更新了一次星历参数，可以尝试使用不同星历的观测数据段分别构建各自的标准脉冲轮廓，本文暂不讨论这种处理方法。图4中并没有出现线性项，说明Crab脉冲星射电计时模型参数对于一个月的X射线观测数据比较准确，计时残差主要由观测白噪声引起。当然，可以对计时残差进行二次多项式拟合，得到更新后更加准确一点的自转模型参数［16］。

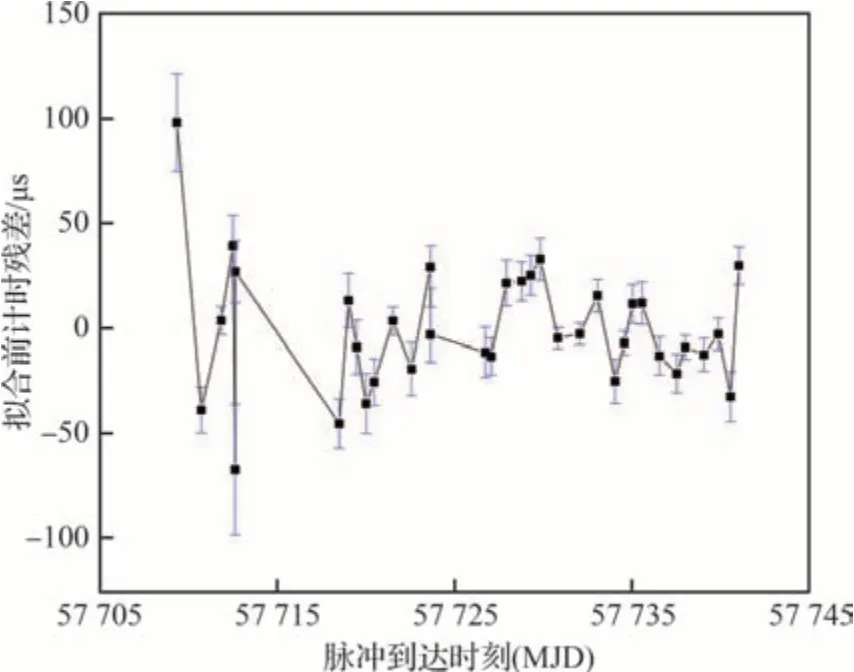
图4 拟合前计时残差Fig. 4 Pre-fit timing residuals

2 X射线脉冲星校准星载原子钟

2.1 参考钟对脉冲星计时的影响

对于X射线脉冲星观测而言，星载原子钟的稳定度与准确度会影响光子到达探测器时刻的测量精度。在理想情况下，原子钟频率源的输出信号为频率恒定的正弦波。但由于系统噪声和随机噪声的存在，频率源的实际输出频率会偏离其标称频率，瞬时相对频率偏差y(t)的定义为

式中：f(t)为频率源的输出频率；f0为标称频率；x(t)为原子钟实际输出信号相对于理想时间信号的时间偏差，可以表示为［25］

式中：x0为初始时刻时间偏差；y0为初始时刻相对频率偏差；a为原子钟频率漂移；xr(t)为随机噪声项。由于频率源输出频率的不稳定以及航天器所处空间磁场环境的变化，星载原子钟的输出频率与标称频率之间会存在一个频率偏差，该偏差值会影响航天器本地时间的准确度。

XPNAV-1卫星直接接收GPS卫星发播的系统时间。GPS时是GPS信号的时间基准，由地面监控站和卫星上的原子钟经加权算法得到［26］。GPS卫星轨道高度约为20200 km，星载钟主要受广义相对论的“引力红移”效应，若卫星发射之前星载钟未作频率调整，GPS卫星钟的走时将比地球时（TT）快。为使GPS钟的走时速率与TT一致，GPS卫星发射前将对原子钟进行频率调整，扣除相对论效应，不再以SI秒为单位测量原时。这种方法的优点是无需考虑地球的引力场及卫星相对于地心的速度对星载原子钟走时速度的影响。但这种时间接收方法只适用于地球表面的近地空间，对于更广阔的太阳系以及星际空间，由于距离问题，航天器无法接收到GPS信号，只能通过携带的星载钟来计时。对于XPNAV-1卫星，若用星载原子钟记录光子到达时刻，则需要考虑广义相对论的时空线元和度规，将原时转化为坐标时，并最终转为TDB。对于地球轨道卫星，原时到坐标时转换公式为［27］

式中：U为地球在卫星处产生的引力势大小，卫星所处的引力势与卫星的位置有关；v为卫星相对于地心的速度；c为光速。TT与地心坐标时（TCG）的关系为［28-30］

式中：LG≡6.969290134×10−10为一常数。若卫星飞行轨道近似为圆轨道，则卫星所处的引力场可视为常数。由式（7）与式（8）可得原时与地球时的关系：

式中：G为引力常量；M为地球质量；r为地球半径；H为卫星的轨道高度。若XPNAV-1卫星使用自己携带的原子钟，经计算，星载原子钟相对于TT走时的变化率为−2.6941×10−10。

对于各种波段的脉冲星计时观测，TOA是由参考钟记录的，进而通过时间转换溯源到更高精度的时间尺度。脉冲星的计时残差方程［2］：

原子钟的钟差、频率偏差、频率漂移均会使记录的光子到达时刻不准确，最终分别导致拟合前计时残差存在常数偏差、线性项以及二次项。式中：R为t时刻的计时残差；R0为t0时刻的残差；∆v0和∆v̇分别为v0、v̇的修正量；∆α、∆δ分别为对脉冲星赤经、赤纬的修正；μα、μδ分别为赤经方向上的自行与赤纬方向上的自行；A、B为脉冲星位置修正项的系数。

为研究星载时钟的频率偏差对X射线脉冲到达时间的影响，本文仿真了参考时钟存在频率偏差时脉冲星光子到达探测器的时刻，这里钟的相对频率偏差取为y0=2.6941×10−10，即卫星星载钟原时与TT速率的相对偏差。此时，第i个光子的到达时间变为

式中：ti表示参考时没有频率偏差时第i个光子的达到时间。

按照X射线脉冲星计时流程重新做处理，得到拟合前计时残差，注意，这里依然用了参考时没有偏差时构建的标准脉冲轮廓，这是为了避免参考钟偏差引起的标准脉冲轮廓变形和信噪比的降低，而这在实际情况中是比较容易做到的，只需利用Crab脉冲星时间校准过的历史数据构建标准脉冲轮廓即可。同时，为了避免复杂性，后面的讨论和计算不考虑分段构建标准脉冲轮廓的情况。对计时残差进行线性拟合，拟合结果如图5所示，拟合斜率为2.6858×10−10，拟合斜率的不确定度为4.2842×10−14。从拟合结果可以看出，通过计时残差的拟合斜率值可估计原子钟的相对频率偏差。因此，可通过X射线脉冲星观测自主校准星载钟的频率偏差，在一定程度上保证星载原子钟的准确度。而通过相对密集的频率驾驭，还可以提高星载钟的稳定度。需要指出的是，本文是基于真实观测数据仿真了记录光子到达探测器时刻的原子钟存在的频率偏差，这只改变了光子到达时刻的时间溯源，并没有仿真脉冲星信号的本身，因此完全保留了实测数据的噪声特征。

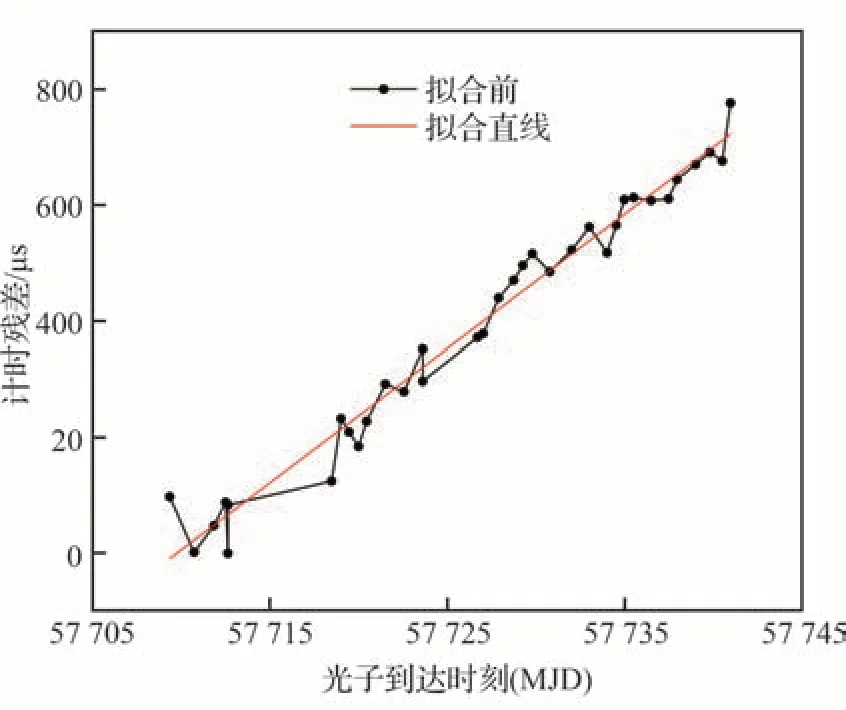
图5 星载钟存在频率偏差时的计时残差及线性拟合结果Fig. 5 Timing residuals and linear fitting results of spaceborne clock with frequency deviation

2.2 不同N值确定的相对频率偏差

考虑到不同bin数对脉冲星计时残差的影响较大，计算了当参考钟存在频率偏差，N取不同值时相对频率偏差估计值yc的变化情况，结果如表3所示，同时给出了相对频率偏差的相对误差δyc：δyc=（yc−y0）/y0。由表3可知，N取值不同，频率偏差估计值与实际设定值之间的偏离程度不同。若N取的太大，则脉冲轮廓信噪比太低，会影响脉冲到达时间的测量精度；若N取的太小，则脉冲轮廓会过于平滑，将间接掩盖频率偏差引起的计时残差的系统性趋势。当N取的过大时，随着N的增加，频率偏差估计值与实际设定值之间的相对误差也随之变大。因此，对于钟差漂移的修正，N要取合适的值。也同时给出了脉冲轮廓经高斯平滑后得到的相对频率偏差估计值ys及其与实际设定值的相对误差δys。比较δyc和δys可知，脉冲轮廓经核回归处理后可有效改正脉冲轮廓低信噪比对频率偏差估计精度的影响。为了更加直观地反映相对频率偏差估计值随N值的变化，图6给出了相对频率偏差估计值与实际设定值的差值（即绝对误差）随N的变化趋势。如图6所示，当N>512时，yc误差的绝对值随N增大而增大；而ys基本不随N值的变化而变化，即对N的取值不敏感。因此平滑脉冲轮廓有利于减小结果对N值的依赖性。由表3给出的相对频率偏差估计值与实际设定值之间的相对误差可知，如果不平滑脉冲轮廓，则N最好≤512。

表3 不同子相位间隔数对应的频率偏差估计值及其相对误差Table 3 Estimates of frequency deviations correspond‑ing to different sub-phase intervals and their relative errors

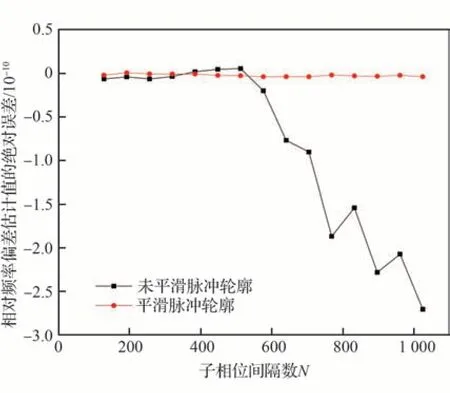
图6 相对频率偏差估计值的绝对误差随N的变化Fig. 6 Variations of absolute error of estimated relative frequency deviation along with values of N

2.3 驾驭不同水平的星载原子钟

基于脉冲星观测估计的星载钟频率偏差的不确定度依赖于脉冲星的TOA测量精度。Crab脉冲星属于正常年轻的脉冲星，TOA测量误差比较大，且其存在周期跃变现象，自转稳定性远低于毫秒脉冲星。遗憾的是XPNAV-1测量不到毫秒脉冲星的周期信号。下面，基于Crab脉冲星的观测，讨论一下其驾驭星载原子钟频率偏差的性能。假设星载钟存在10−10、10−11和10−12这3个不同量级的相对频率偏差，N=256，并利用高斯核回归平滑脉冲轮廓，所得结果如表4所示。由表4可知，随着频率偏差量级的减小，该方法得到的频率偏差估计值与真值的偏离程度变大。这是由于Crab脉冲星TOA测量精度不高，导致频率偏差较小时对其估计精度偏低。在实际应用过程中，可通过观测自转更加稳定的毫秒脉冲星，获得更高精度的星载钟频率偏差值。另一方面，选用的Crab脉冲星的数据长度只有1个月左右，如果数据时间跨度更长，则其检测星载钟相对频率偏差的性能会更高。当然，实际情况中星载钟还可能存在频率漂移，那就需要做二次多项式拟合，并通过拟合的多项式系数改正星载原子钟的钟差、频率偏差及漂移项。由于所用数据比较短，在模拟钟差时只考虑了线性的频率偏差。

表4 相对频率偏差取值不同对应的改正结果Table 4 Correction results corresponding to different values of relative frequency deviation

在得到星载钟相对频率偏差的估计值之后，据此可以驾驭星载钟的频率，改正其频率偏差，使之输出更准确的时间。具体过程是：根据脉冲星拟合前计时残差的拟合斜率，即星载钟频率偏差估计值ys，将星载钟的相对频率偏差反向补偿一个因子(1+ys)；驾驭后星载钟的等效输出频率为f′=f(1+ys)，其中f是未经驾驭的星载钟的输出频率。这样就在一定程度上校准了星载钟的频率偏差，提高了其准确度。图7给出了星载钟无频率偏差时拟合前计时残差和星载钟有频率偏差又被脉冲星驾驭频率修正后的计时残差的比较。这个结果用了N=256时的相对频率偏差估计值2.6858×10−10。从图7可以看出，计时残差不含明显的趋势项，与参考钟没有频率偏差时得到的计时残差相比，二者的变化趋势基本一致。

图7 参考钟经频率偏差修正后的计时残差Fig. 7 Timing residuals after correction of reference clock frequency deviation

3 结 论

针对XPNAV-1卫星公开的数据，分析了利用Crab脉冲星驾驭空间原子钟频率的可行性。通过比较3种核回归方法对脉冲轮廓的平滑能力，发现Gaussian核回归可以更加有效地降低脉冲轮廓中的随机噪声并保留信号的峰值特征，提高了计时精度。基于此，仿真了星载原子钟存在频率偏差时的光子到达时刻数据，研究了钟的频率偏差对TOA及计时残差的影响。结果表明钟的频率偏差会使计时残差产生线性变化趋势，对其线性拟合获得了参考原子钟的相对频率偏差。我们计算了不同bin数的结果，发现脉冲轮廓经过高斯核回归法平滑后，得到的参考钟相对频率偏差拟合值基本与bin数无关，这减小了因N的取值不同带来的不确定性，即提高了脉冲星频率驾驭的稳定性。通过对参考原子钟的频率驾驭，可校准其频率偏差，提高其准确度。通过分别仿真星载钟10−10、10−11和10−12水平的相对频率偏差，一月数据长度的Crab脉冲星校准星载钟频率的相对误差分别为0.3%、42%和113%。

下一步，如果能够利用更长时间跨度的Crab脉冲星计时数据，有利于降低或消除脉冲星本身的噪声或其他具有周期性的影响因素，进而提高相对频率偏差的估计精度。目前星载原子钟频率准确度已达到10−12量级甚至更高，为此必须提高脉冲星检验星载钟频率偏差的水平，这需要观测自转更加稳定、计时精度更高的X射线毫秒脉冲星，预期可以大大提高星载钟的频率校准精度。当然，这需要灵敏度更高的X射线探测器。

通过密集的原子钟频率驾驭，还可以提高其长期稳定度。因此，本文的研究有利于提高空间时间系统的长期自主保持能力。