基于扩维QLEKF的脉冲星/星间定向组合导航

熊凯，魏春岭，李连升，周鹏

北京控制工程研究所 空间智能控制技术重点实验室，北京 100094

卫星星座是为完成特定空间任务而协同工作的多颗卫星。作为卫星星座的典型代表，北斗卫星导航系统承担国家时空基准建立与维持、定位导航授时信息播发等关键任务。在未来相当长的时间内，将作为国家综合定位导航和授时（Positioning， Navigation and Timing，PNT）体系的核心空间基础设施，服务于国民经济发展和国防建设。卫星星座系统除了要求实现很高的定位精度外，还要求具有较强的长期自主运行能力。尽管基于地面测控的导航定位系统具有精度高、技术成熟等优点，但该导航方式主要依赖外部人造信标进行工作，从一定程度上削弱了星座系统的自主性。不依赖地面测控的自主导航技术是新一代星座系统的研究重点之一。

脉冲星是宇宙空间中以稳定的周期高速自转的中子星，被誉为“宇宙中的灯塔”“自然界最精确的天体钟”。X射线脉冲星导航系统基于在航天器上配置的X射线探测器，测量脉冲星辐射的以稳定周期变化的光子信号，提取脉冲到达时间（Time of Arrival，TOA）观测量，经过数字信号处理实现航天器自主PNT［1-4］。X射线脉冲星导航是一项极具发展潜力的技术，其可行性已通过在轨试验得到验证［5-8］。但是，由于到达航天器的脉冲星信号非常微弱，受X射线探测器有效面积等因素的限制，仅依赖脉冲星导航难以满足星座系统对导航精度的要求。通过多源测量信息融合，能够达到比单独X射线脉冲星导航更高的定位精度水平［9-11］。

基于照相观测的星间定向技术是星座自主导航研究的重要成果之一，基本方法是在星座卫星上配置具有跟踪指向功能的照相观测星相机，测量相邻星座卫星的视线方向矢量，进而，利用射频或激光链路，通过双向测距等技术手段获得星间距离信息，从而得到星间相对位置观测量。根据基于相对测量的绝对定轨理论方法，利用星间相对位置观测量，结合航天器轨道动力学，通过设计适当的导航滤波器，能够实现对星座卫星绝对位置和速度的估计［12-14］。将X射线脉冲星导航和星间定向观测技术相结合，构成组合导航系统，能够充分发挥不同方法各自的优势，使组合系统性能优于各子系统，是实现高精度高可靠自主导航的有效途径。

X射线脉冲星/星间定向观测组合导航研究面临的问题之一在于，星座卫星轨道动力学方程是在地心惯性系中建立的，而脉冲星观测模型是在太阳系质心（Solar System Barycenter，SSB）坐标系中建立的。在数据处理过程中，为了利用星座卫星位置矢量的估计值计算脉冲星观测量的预测值，需要用到地球相对于SSB的位置信息。受现阶段测量技术条件的限制，根据星历计算得到的地球位置存在误差。文献［15］分析了星历误差造成的系统偏差对脉冲星导航性能的影响。文献［16-17］研究了通过脉冲星观测量差分技术削弱星历误差影响的方法。考虑到通过不同观测量相减得到的差分脉冲星观测量的噪声相对较大，文献［18］设计了针对星历误差的鲁棒卡尔曼滤波器导航定位方法，通过优化滤波器中增益阵的计算来提升导航性能。

此外，在卡尔曼滤波器设计过程中，要求系统数学模型是准确的，系统噪声和测量噪声为统计特性已知的高斯白噪声。在星座自主导航系统中，通过轨道动力学方程描述星座卫星的运动规律，将轨道动力学方程中的未建模误差项视为系统噪声；将系统噪声作为高斯白噪声进行处理，是对实际情况的一种近似。在系统噪声统计特性存在不确定性的情况下，如何优化选取扩展卡尔曼滤波器（Extended Kalman Filter，EKF）的设计参数，是自主导航研究中的一个共性问题。

针对上述问题，将地球位置矢量扩充为状态，设计了面向X射线脉冲星和星间定向观测量处理的扩维EKF算法，通过计算导航系统的克拉美劳下界（Cramer-Rao Lower Bounds，CRLB），对扩维后系统的可观度进行了分析。进而，针对EKF递推计算公式中的系统噪声方差阵取值影响估计精度的问题，引入Q学习方法实现滤波器参数整定，设计了Q学习扩展卡尔曼滤波器（Q-Learning Extended Kalman Filter，QLEKF）。最后，通过仿真验证星座自主定位精度水平。

1 组合导航系统模型

1.1 脉冲星导航观测方程

X射线脉冲星导航通常以SSB为空间参考点，脉冲星发射的脉冲信号到达SSB的时间可以精确预报，脉冲信号到达卫星的时间可以通过星上X射线探测器测量得到，脉冲信号到达卫星与到达SSB的时间之差反映了卫星相对SSB的位置矢量在脉冲星视线矢量上的投影，如图1所示，图中n(p)为脉冲星视线方向矢量；c为光速，c=299792458 m/s；和分别为脉冲信号到达航天器和太阳系质心的时间；rsm和rE分别为航天器和地球相对于太阳系质心的位置矢量；rm为航天器相对于地心的位置矢量。X射线脉冲星导航的主要优势体现在：以在天球上分布的脉冲星为导航信号源，不依赖近天体的可见性，适用范围广，可用于近地轨道、星际飞行航天器及无稠密大气行星表面巡视器等，并且具有潜在的长期自主守时能力。

图1 脉冲到达时间与卫星位置矢量的关系Fig.1 Relation between pulse time of arrival and posi⁃tion vector of satellite

假定X射线探测器安装在星座卫星的指向机构上，对作为导航信号源的X射线脉冲星进行观测。基于脉冲星时间转换模型建立起来的第p颗脉冲星的观测方程为

式中：上标(p)用于区分不同的脉冲星为对应第p颗脉冲星的观测量为第p颗脉冲星发射的脉冲信号到达SSB的时间，可通过事先建立的脉冲星时间模型预测得到为同一脉冲信号到达星座卫星的时间，可以通过X射线探测器测量得到为测量函数；xk为状态向量，由参与导航的星座卫星的位置矢量和速度矢量构成为均值为0、方差为的测量噪声。将测量函数表述为

式中：rE，k为地心相对于SSB的位置矢量；rm，k为第m颗星座卫星相对于地心的位置矢量。

根据脉冲星导航的观测方程不难看出，脉冲到达时间观测量反映了卫星位置信息。结合卫星轨道动力学模型，通过EKF处理一个时间序列上的观测量，可以获得航天器位置和速度的估计值。值得注意的是，地球相对于SSB的位置根据星历进行预报，存在星历误差的情况下，地球预报位置和真实位置之间存在偏差，参照式（2），这会导致观测方程中出现系统偏差，从而对导航结果产生不利影响，需要优化导航滤波器的设计，以削弱地球星历误差的影响。

1.2 星间定向观测方程

基于照相观测的星间定向是高精度星座自主导航的实现方式之一，基本方法是在部分星座卫星（称为观察卫星）上配置具有跟踪指向功能的星相机，对相邻星座卫星（称为目标卫星）视线（Line of Sight，LOS）方向矢量进行观测，结合星间链路伪距测量得到星间相对位置观测量；结合卫星轨道动力学模型，采用EKF或其改进算法，根据一个时间序列上的观测量，对参与导航的星座卫星的位置和速度矢量进行估计。该导航方式的特色在于：仅依赖星间相对测量信息确定星座卫星的绝对位置，在导航解算过程开始之前，目标卫星和观察卫星的位置均不要求精确已知，二者的概略位置信息满足目标卫星进入星相机视场的跟踪捕获要求即可。

基于照相观测的星座自主导航精度在很大程度上取决于在地心惯性系中目标卫星视线方向的测量精度。利用配置了星相机设备的观察卫星对目标卫星实施照相观测的示意图如图2所示。

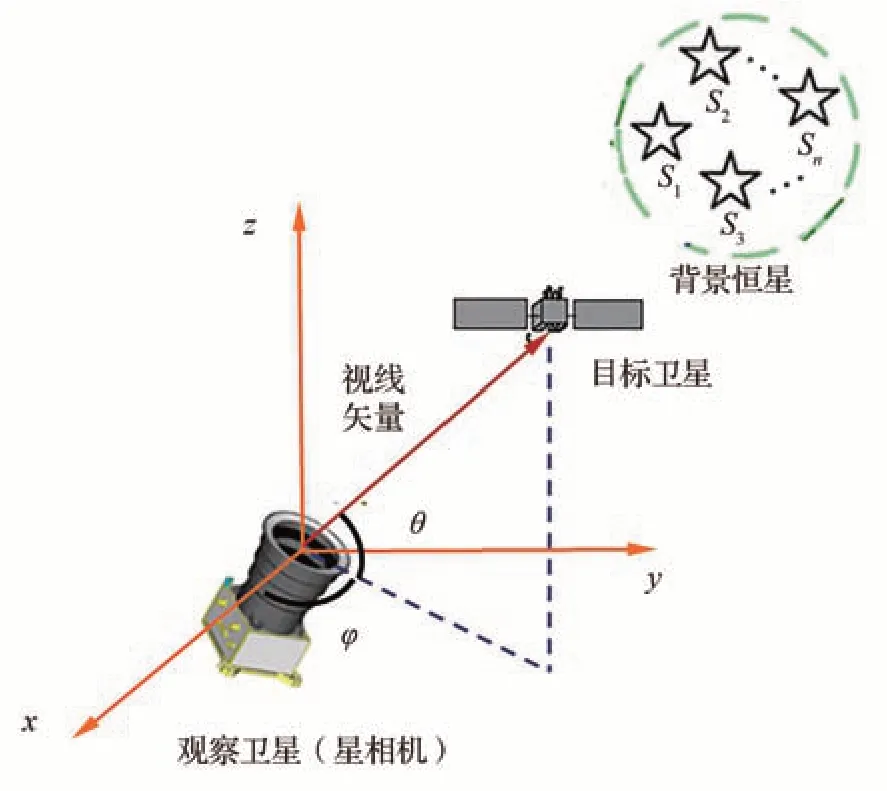
图2 目标卫星和背景恒星的观测Fig. 2 Observation of target satellite and background stars

相对基于近天体和远天体观测的传统天文测角导航方式［19］，星间定向观测的主要优势体现在：通过小视场长焦距星相机测量目标卫星的视线方向，易于通过优化光学系统设计实现较高精度，从而提升导航系统性能，避免大视场敏感器测量近天体中心方向时精度受限的问题。

星相机的探测背景是恒星，考虑到恒星在地心惯性坐标系中的角位置是固定的，并且其视线方向矢量信息可根据恒星星表精确得到，采用星相机照相观测的方式同时对目标卫星和背景恒星成像，根据目标卫星在星相机中的成像相对于背景恒星成像的几何位置关系，通过最小二乘法可以直接计算得到目标卫星在惯性系中的视线方向矢量。采取基于照相观测的目标卫星定向测量方式，不必用到观察卫星平台的姿态确定信息，可以避免目标卫星视线方向测量精度受观察卫星姿态确定精度的影响，有助于减少潜在的误差源，实现目标卫星视线方向的高精度测量。

将用于描述某个星间视线方向矢量的观测方程写为

根据观测方程式（4）不难看出，观测量反映了惯性系中目标卫星相对于观察卫星的位置矢量，结合航天器轨道动力学模型，可用于确定星座卫星的绝对位置矢量rm，k和rn，k。应当说明，对于星间距离较远的情况，应设法补偿观测方程中光子传播时间的影响［20］。

1.3 卫星轨道动力学方程

由3颗地球卫星构成的星座示意图如图3所示。星座卫星主要在地球重力场的作用下在轨运动，在每颗星座卫星上配置X射线探测器和星相机，对X射线脉冲星和目标卫星实施跟踪观测。为了简单起见，以包含3颗卫星的星座为例进行说明，尽管如此，所述方法可以推广用于星座中包含多颗卫星的情况。

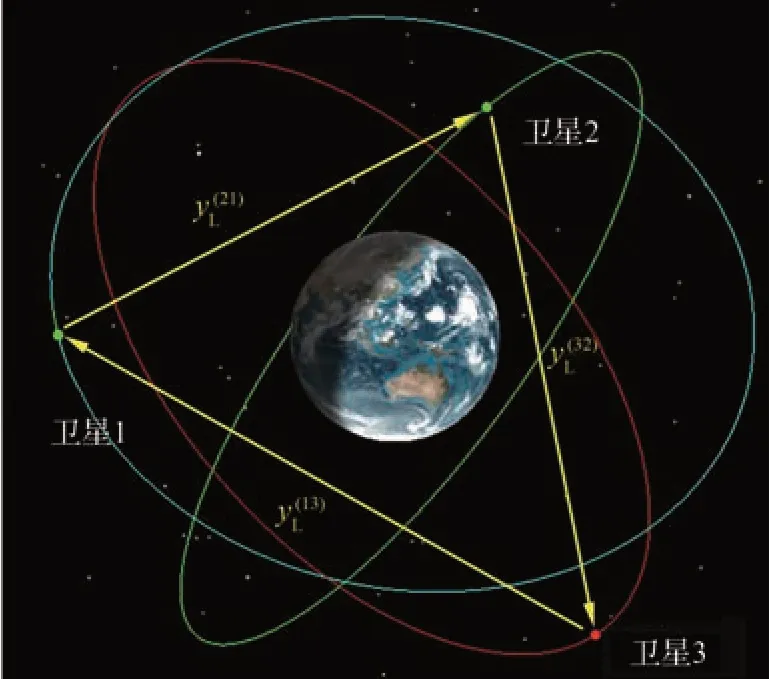
图3 由3颗卫星构成的星座Fig. 3 Constellation consisting of three satellites

星座卫星的运动状态演化情况通过轨道动力学方程来描述，其形式为

式中：vm，k为第m颗星座卫星的速度矢量；μE为地球引力常数；函数p(rm，k)为除地球质心引力以外，星座卫星受到的其他摄动加速度的影响，如对于中高轨卫星通常包括地球非球形引力摄动、太阳光压和日/月引力摄动等；τ为一步状态预测的时间步长。系统噪声wm，k用于描述状态方程与实际系统之间的差异，假设其均值为0、方差阵为Qm，k。

2 扩维扩展卡尔曼滤波器

2.1 状态扩维

对于X射线脉冲星/星间定向观测组合导航，常规的处理方式是根据式（6）建立状态方程，根据式（1）和式（4）建立观测方程，设计EKF算法，对观测量进行处理，获得星座卫星位置矢量和速度矢量的估计值。但是，在脉冲星导航观测方程中，不仅包含随机误差，还包含地球星历误差造成的系统偏差。与随机误差相比，系统偏差对星座卫星导航性能的影响要大得多。原因在于，随机误差的影响可视为高斯白噪声，通过EKF在最大程度上予以削弱；而系统偏差如果不能在模型中有效地体现出来，将呈现为观测方程的不确定性，其影响不能直接通过EKF消除，会导致滤波器的状态估计值偏离真实状态，使得导航系统性能下降。如何减小系统偏差的影响是实现高精度自主导航的关键。

系统偏差在轨校准是提高星座导航精度的重要手段。事实上，通过优化导航滤波器的设计，不仅能够削弱敏感器随机误差的影响，而且能够对部分系统偏差进行校准。为了实现这一目的，需要对系统偏差进行建模，基本原则是要求模型尽可能精确地反映系统偏差的变化规律，典型做法是将系统偏差描述为若干模型参数的函数形式；进而，将模型参数扩充为状态向量，设计扩维EKF，利用敏感器观测量对模型参数进行实时估计，并根据模型参数的估计值实现系统偏差校准，从而削弱系统偏差对导航精度的影响。

在航天器自主导航研究领域，滤波器的状态扩维是处理系统偏差最常用的手段之一。尽管如此，扩维EKF的引入也带来了一些新的问题：首先，将地球的位置和速度矢量扩充为状态进行估计，为了保障扩维EKF的性能，要求扩维后的系统具有较高的可观度；如果扩维后的系统不可观，那么，状态估计结果将是不可信的。对扩维后的系统进行可观度分析，是自主导航系统方案设计的重要环节。为此，通过计算CRLB对受地球星历误差影响的星座自主导航系统的可观度进行分析。其次，在用于描述系统偏差的模型参数被扩充为状态向量后，如何确定扩维后系统的系统噪声方差阵，这是滤波器设计过程中需要解决的问题。对于工程技术人员而言，滤波器参数整定往往是一项耗时费力的工作，且通过地面仿真和试凑得到的滤波器参数不一定适用于在轨应用的情况。对于这一问题的解决策略，将在第3节进行探讨。

扩维EKF的状态向量由参与导航的3颗星座 卫 星 的 位 置r1，k、r2，k、r3，k，速 度 矢 量v1，k、v2，k、v3，k以及地球的位置rE，k和速度矢量vE，k构成：

地球的运动状态演化规律通过相应的轨道动力学方程来描述。为了便于导航滤波器的设计，将扩维后系统的状态方程写为离散时间非线性随机系统模型的形式：

式中：

其中：pE(rE，k)为除太阳引力外，太阳系中木星等其他天体摄动加速度的影响；wk为系统噪声，式（8）中未建模误差项的影响，假设其方差阵为Qk。参照式（1）和式（4），易得到组合导航系统观测方程的标准形式：

式中：yk为X射线脉冲星和星间定向观测量；h(xk)为相应的测量函数；νk为测量噪声，假设其方差阵为Rk。

2.2 CRLB分析方法

针对星座自主导航中扩维系统性能分析问题，说明CRLB的计算方法。CRLB是根据给定的随机系统模型、状态向量先验信息及噪声统计特性计算得到的实际状态估计误差方差阵下界的理论值。该取值反映了一个导航系统的本质属性，可以用于衡量系统可观度的大小。通过计算CRLB，能够针对所研究的导航系统，给出理想情况下的状态估计精度极限，从而为导航方案选择提供参考依据［21-22］。如果状态向量中的某些元素对应的CRLB不收敛，则说明导航系统自身设计存在缺陷，该问题不能通过优化滤波器自身的设计得到解决，而应当考虑改进系统模型、减少状态变量或引入新的测量信息。

相对于传统的系统可观性分析方法［23］而言，基于CRLB的导航系统性能分析方法的优势主要体现在以下几个方面：首先，CRLB计算是针对状态向量中的各个元素进行的，利用CRLB能够辨别出系统中哪些状态能够得到准确估计，哪些状态的估计不收敛；所取得的结论可以用于导航系统模型或敏感器配置的改进。其次，借助CRLB不仅能够对线性系统的性能进行分析，还能方便地对非线性系统的性能进行分析。再次，通过CRLB计算得到的是定量结果，即给出状态估计器的潜在精度水平。

对于如式（8）和式（10）所示的随机系统，根据观测序列{yk，k=1，2，…}对状态向量xk进行估计，得到状态向量估计值，那么状态向量估计误差=−xk的CRLB的简便计算方法为

式中：Jk为信息矩阵。信息矩阵可根据式（12）进行递推计算：

信息矩阵的初始值J0可根据有关估计误差统计特性的先验知识确定，如令J0=P−10，其中，P0为初始估计误差方差阵。在第4节给出了对扩维后系统的状态估计理论精度进行CRLB分析的结果。

2.3 导航解算流程

对于X射线脉冲星/星间定向观测组合导航系统，根据如式（8）所示的状态方程及如式（1）和式（4）所示的观测方程，设计得到的扩维EKF算法流程如图4所示，其中，为状态向量的预测值；Pk为估计误差方差阵；Pk|k−1为预测误差方差阵；为脉冲星测量噪声方差；为脉冲星测量 新息；为星间 定向测量 新 息；KX，k和KL，k分别为X射线探测器和星间定向观测的卡尔曼增益。和为状态方程和观测方程的雅可比矩阵。

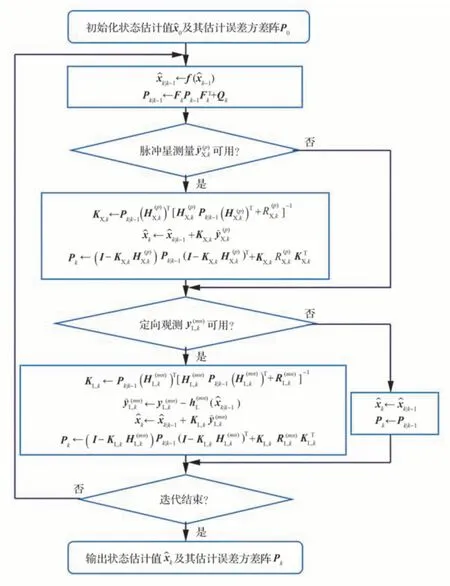
图4 基于扩维EKF的组合导航算法框图Fig. 4 Diagram of integrated navigation algorithm based on augmented EKF

在导航滤波器的一个递推计算周期内，如果X射线探测器或星间定向测量设备的输出信息可用，则利用其对状态向量进行修正；如果二者皆不可用，则仅对状态向量进行预测。预测和更新的过程反复迭代进行，实现对星座卫星运动状态的实时估计。上述处理方式的优势是设计简单、应用方便。

3 Q学习扩展卡尔曼滤波器

3.1 设计思路

如何在有效削弱模型不确定性影响的同时，尽可能控制滤波器的复杂程度，是从事导航系统研究的工程技术人员经常遇到的问题。强化学习理论方法和应用技术的进步，为导航滤波器的优化设计提供了新的解决方案。作为强化学习中得到广泛应用的方法之一，Q学习的基本思路是通过智能体（Agent）在未知环境中通过反复迭代的试错（Trial and Error）过程不断积累经验，逐渐使得累积奖赏（以数表或其他形式的Q函数来表述）最大化，最终掌握一种选择动作的最优策略［24-26］。Q学习方法在环境探索和问题决策等方面具有优势，在随机系统状态估计领域，结合卡尔曼滤波器的估计能力和Q学习方法的决策能力，有助于提升滤波器对不确定模型的适应性［27］。将Q学习用于导航滤波器的设计，使得滤波器可以通过自身与环境的交互，自适应地选取合理的滤波器参数，在实际应用过程中逐渐改善状态估计精度，从而增强导航系统的任务能力。

探讨Q学习方法在导航滤波器设计中的应用，主要考虑系统噪声的统计特性存在不确定性的非线性系统，设计了一种Q学习扩展卡尔曼滤波器，特色是将Q学习方法用于EKF参数整定。为了突出重点，以如式（8）和式（10）所示的系统模型为例进行算法编排。进而，在第4节以基于X射线脉冲星和星间定向观测的星座自主导航系统为例，展示了QLEKF所能产生的有益效果。

为了清楚起见，将QLEKF的主要思路归纳如图5所示，其中，和为基准滤波器的状态估计值及其误差方差阵；为根据Q函数采取ε贪心策略选择的噪声方差阵；和分别为搜索滤波器和基准滤波器的测量新息。

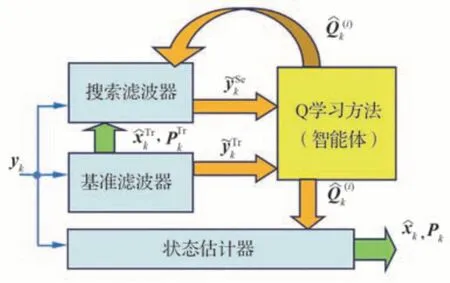
图5 Q学习扩展卡尔曼滤波器结构Fig.5 Structure of Q-learning extended Kalman filter

QLEKF采取基准滤波器、搜索滤波器和状态估计器并行计算的结构形式。基准滤波器、搜索滤波器和状态估计器均采取EKF的滤波方程，在真实系统噪声方差阵Qk未知的情况下，在基准滤波器中，利用系统噪声方差阵标称值Qˉk进行滤波解算；在搜索滤波器中，根据智能体当前获得的累积奖赏（Q函数），通过查表的方式，在根据先验知识建立的模型集中选择作为滤波器的系统噪声方差阵；状态估计器中的系统噪声方差阵也通过Q学习得到。状态估计器与搜索滤波器的不同之处在于：搜索滤波器的状态估计值及其误差方差阵每隔一个固定迭代次数T，以基准滤波器为准进行重置，而在状态估计器中不进行状态估计值及其误差方差阵的重置。在Q学习中，通过搜索滤波器和基准滤波器测量新息的比对构造奖赏。测量新息的幅度可视为滤波器性能优劣程度的征兆。通常滤波器的测量新息较小意味着潜在的状态估计精度较高；相反，滤波器的测量新息较大意味着潜在的状态估计精度较低。随着递推计算过程的进行，智能体将趋向于选择能够带来较大累积奖赏的系统噪声方差阵，根据所设计的奖赏，预期智能体选择的系统噪声方差阵有助于提升状态估计精度。

3.2 算法编排

基于3.1节描述，给出QLEKF的递推计算流程，如图6所示，其中和为搜索滤波器的状态估计值及其误差方差阵；Q(s，a)为智能体的状态s和动作a的Q函数，可写为数表的形式，其中，s对应不同的系统噪声方差阵，a对应在数表中探索的动作；S和A分别为状态集和动作集；R(s，a)为奖赏；函数ε-greedy为选择动作的ε贪心策略，即以ε的概率在动作集A中随机选择动作，以1−ε的概率选择对应Q函数最大的动作，ε∈(0，1)为事先设定的随机动作选择概率；为状态估计器的测量新息。函数EKF表示扩展卡尔曼滤波器的递推计算公式，其形式可参照图4。在Q函数的递推计算公式中，α为学习速率，0≤α<1；γ为折扣因子，0<γ≤1；ε、α和γ均 为 可 调 参 数；maxa′Q(s′，a′)为 在 状 态为s′的情况下，对于任意动作a′∈A，数表中Q函数的最大值；最终的估计结果为状态估计器的输出和{Pk}。

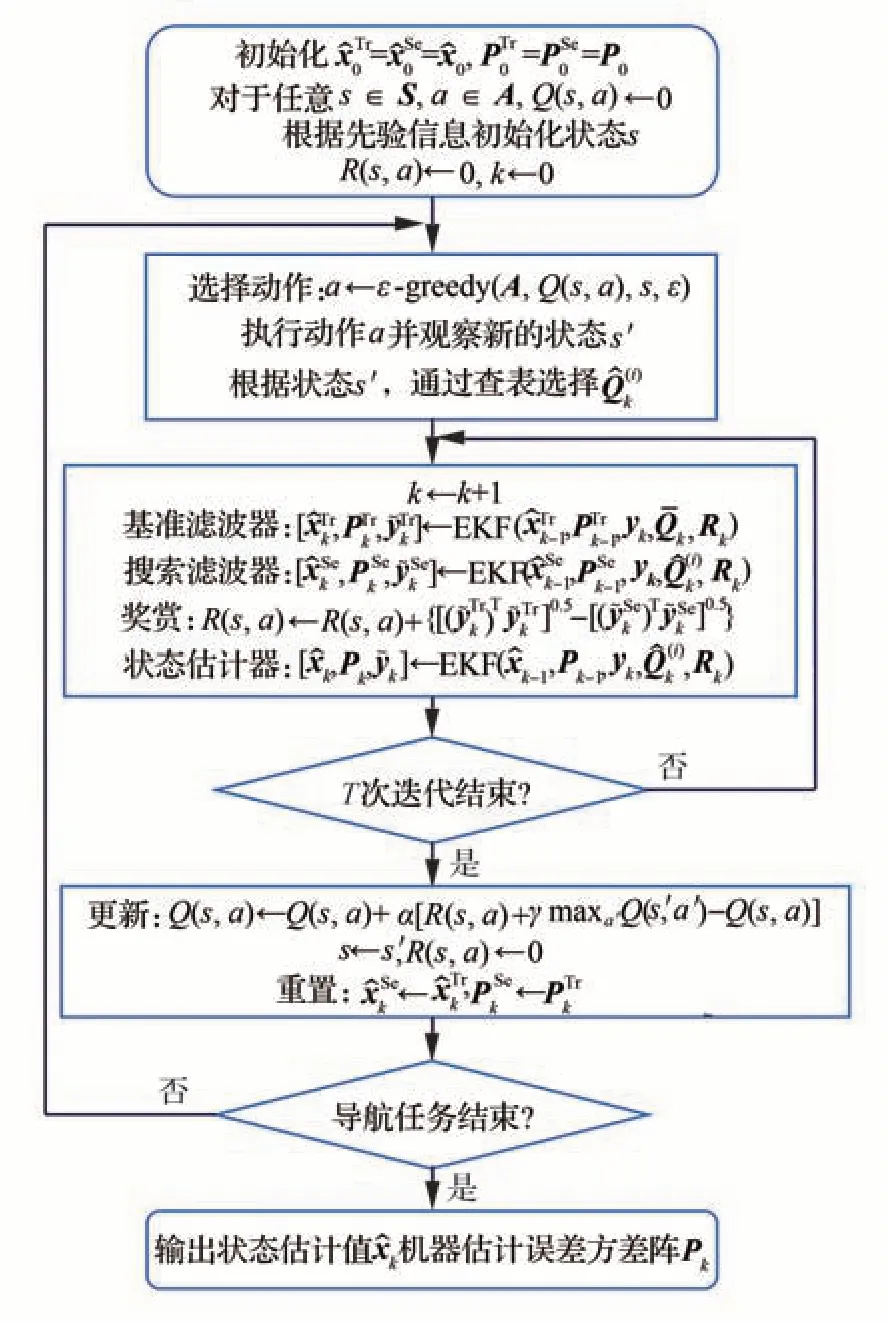
图6 Q学习扩展卡尔曼滤波器算法框图Fig. 6 Diagram of Q-learning extended Kalman filter⁃ing algorithm

4 仿真分析

4.1 仿真条件

针对X射线脉冲星/星间定向观测组合导航系统，通过数学仿真说明所设计的扩维EKF和QLEKF的有效性。在仿真过程中，假设3颗星座卫星的初始轨道参数如表1所示。

表1 星座卫星初始轨道参数Table 1 Initial orbital elements of satellites in constellation

假设在每颗星座卫星上安装1台有效面积为1 m2的X射线探测器，分别对3颗脉冲星B0531+21、B1821-24和B1937+21进行指向观测，观测时间为1000 s。脉冲到达时间观测量的测量噪声标准差根据文献［28］中的经验公式和脉冲星辐射特性计算得到，星间定向观测噪声标准差∈[10 m，500 m]。基本仿真设置如表2所示，表中σr和σv分别为位置矢量和速度矢量的系统噪声标准差；pr和pv分别为位置矢量和速度矢量的初始估计误差标准差。

表2 星座自主导航仿真设置Table 2 Simulation configuration for constellation au‑tonomous navigation

4.2 仿真结果

首先，通过计算CRLB对扩维系统进行可观度分析。对于X射线探测器有效面积A分别为4、1、0.25 m2及星间定向观测噪声标准差σ分别为10、100、500 m的情况，对应地球3轴位置误差的CRLB中各元素的平方根曲线如图7所示，图中rx、ry和rz为位置矢量的3个分量。从图7中易于看出，对于给定的仿真场景，当探测器有效面积和星间定向测量精度在一定范围内变化时，通过CRLB计算得到的理论上的估计误差曲线是收敛的，这说明组合导航方案在扩维系统设计层面是有效的。

图7 地球位置估计误差的CRLBFig.7 CRLB for position estimate error of Earth

其次，分析基于扩维EKF的地球星历误差校准对星座卫星位置估计精度的影响。地球星历误差校准前后，星座中某颗卫星的3轴位置估计误差曲线及其3σ误差界如图8所示。通过仿真结果可以看出，存在地球星历误差的情况下，通过扩维EKF进行校准后，相对于不进行地球星历误差校准的情况，星座卫星位置估计精度显著提升。并且，经过校准，位置估计误差曲线在滤波器估计误差方差阵规定的范围内波动，这体现了导航滤波器设计的合理性。

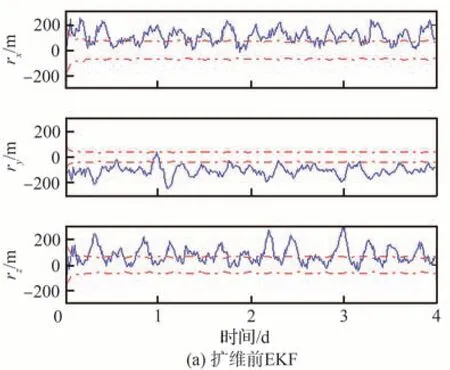
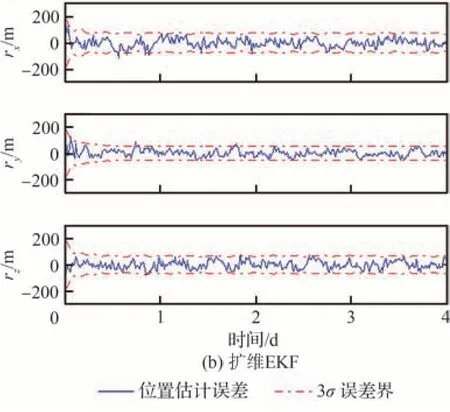
图8 星座卫星位置估计误差曲线 Fig.8 Position estimate error curves of satellite in constellation

为了进一步说明扩维EKF的有效性，通过蒙特卡洛仿真，将其与鲁棒扩展卡尔曼滤波器（REKF）进行了对比研究。利用扩维前EKF、扩维EKF和REKF得到的星座中2颗卫星的位置估计均方根（RMS）误差曲线如图9所示，第3颗卫星的估计结果与之类似。

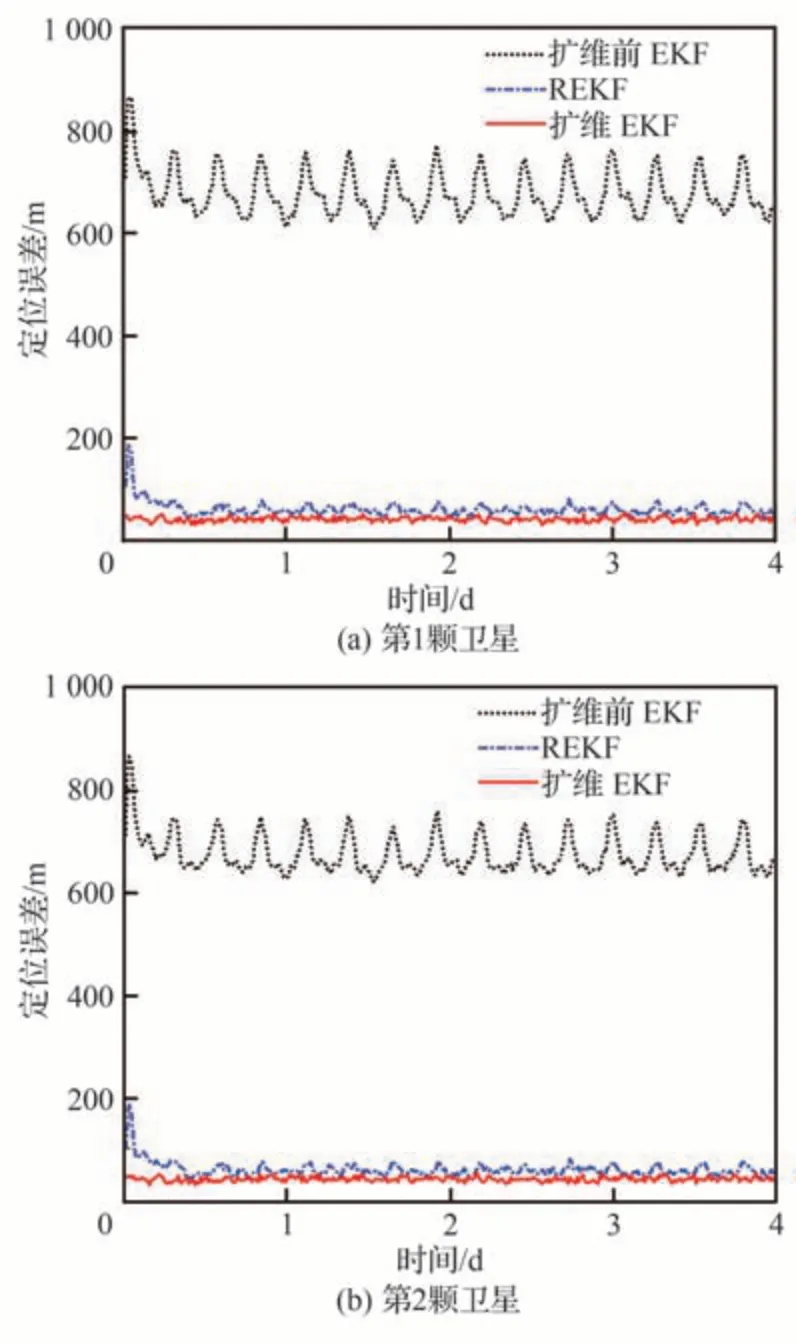
图9 扩维前EKF、REKF和扩维EKF的位置估计均方根误差Fig. 9 Position estimate RMS errors obtained from preaugmented EKF， AEKF and augmented EKF

在扩维系统可观度满足要求的情况下，通过扩维EKF能够实现对模型参数的有效估计，星座卫星位置估计精度优于REKF。通过Q学习方法优化滤波器参数的设计，还能够进一步提升导航系统性能。

为了说明QLEKF的有效性，将其与扩维EKF及常用的自适应扩展卡尔曼滤波器（AEKF）［29］和多模型自适应估计（MMAE）［30］算法进行了对比研究。通过扩维EKF、AEKF、MMAE和QLEKF得到的星座卫星位置估计均方根误差曲线如图10所示。

图10 扩维EKF、AEKF、MMAE和QLEKF的位置估计均方根误差Fig.10 Position estimate RMS errors obtained from augmented EKF， AEKF， MMAE and QLEKF

为了便于对比，将不同滤波算法位置估计均方根误差的平均值归纳如表3所示。仿真结果表明，在X射线脉冲星/星间定向观测组合导航系统中，对于给定的仿真条件，QLEKF能够取得优于扩维前EKF等算法的状态估计精度。值得注意的是，MMAE算法中并行滤波器的数目随模型集中模型数的增加而增长，而设计的QLEKF采取固定3个并行滤波器的结构形式，避免对星上计算机造成较大负担。

表3 星座卫星位置估计精度Table 3 Position estimation accuracy of satellites in constellation

5 结 语

对基于X射线脉冲星和星间定向观测的星座卫星组合导航方法进行了研究。针对地球星历误差影响导航性能的问题，设计了一种基于扩维扩展卡尔曼滤波器的偏差校准和状态估计算法。进而，设计了面向滤波器参数整定的Q学习扩展卡尔曼滤波器，其特色是根据测量新息构造奖赏，在应用环境中逐渐实现滤波器参数优化。仿真研究表明，综合应用所设计的扩维EKF和QLEKF算法有助于提升星座卫星位置估计精度。在下一步工作中，将继续研究Q学习方法中状态集、动作集、奖赏和Q函数的优化设计方法，同时，研究基于自然时空基准的星座原子钟组整体频率漂移校准方法，保障星座系统的长期自主运行能力。