基于GDE混合算法的齿轮系统轻量化设计
2023-03-12国瑞坤高颖贺磊杨先海李元帅李凯
国瑞坤,高颖,贺磊,杨先海,李元帅,李凯
(1.山东理工大学 机械工程学院, 山东 淄博 255049;2.山东理工大学 计算机科学与技术学院, 山东 淄博 255049)
齿轮传动系统是各领域机械的重要组成部分,在国家装备制造业中具有不可替代的作用,其轻量化设计是所属机械减重的重要途径,产生的经济效益十分可观,是实现产品竞争力的有效途径[1]。针对齿轮轻量化,许多学者从结构、材料、齿轮参数优化及优化方法等方面展开了讨论研究。冯顺利[2]通过神经网络算法对权重系数进行调整,利用遗传算法进行了斜齿轮参数优化,解决了优化过程中权重系数分析不合理问题。戴护民[3]运用多目标拓扑优化技术实现了齿轮轻量化设计。车林仙等[4]通过改进差分进化算法得到了更加符合实际的齿轮参数优质解。以上研究涉及改进适应度函数权重、有限元结构设计、算法离散化改进等齿轮轻量化设计方法,都取得了较好的设计结果。本文拟通过遗传算法(genetic algorithm,GA)优化差分进化算法(differential evolution algorithm,DE)的初始种群,提出一种遗传差分进化混合算法(GDE)并进行仿真分析,在验证算法可行性的同时,得到更符合实际工况的轻量化齿轮系统。
1 GDE混合算法的实现
针对GA全局寻优能力强、DE局部寻优能力较差的特点,提出一种GDE混合算法,通过GA进行全局寻优,扩大搜索范围,针对DE容易产生的局部最优解,利用GA较强的全局寻优能力,给DE提供良好的初始值,充分发挥GA与DE的优点,扬长避短,实现算法求解性能的最优化。GDE的具体运行流程如图1所示,运行步骤说明如下:
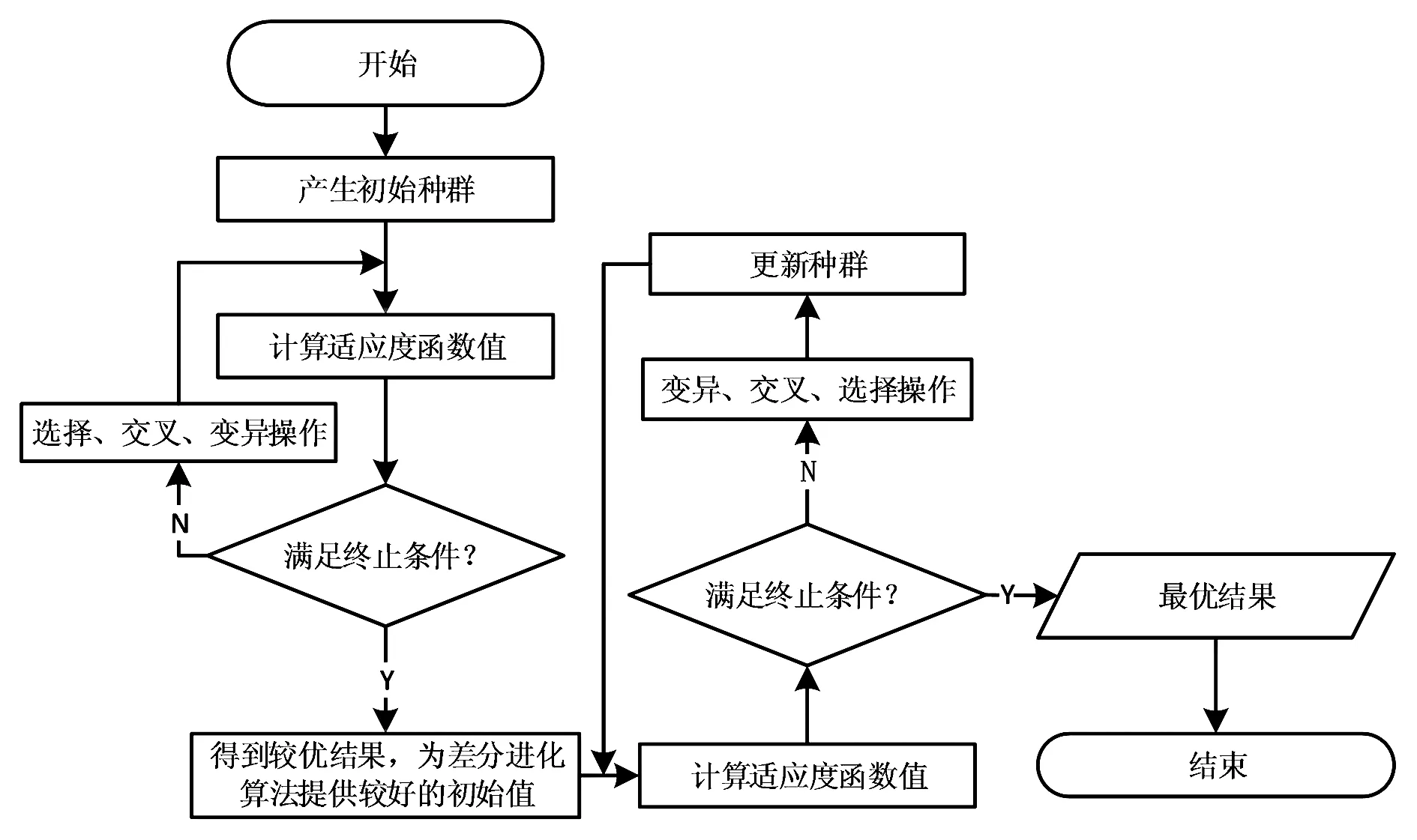
图1 GDE混合算法流程图
步骤1 GA编码并进行约束条件检验,随机产生初始化种群Xn(0)。
步骤2 GA运算适应度函数采用后文介绍的目标函数1,重点考虑中心距最小问题,以获得全局较优的种群。
步骤3 判断是否满足GA种群最大进化代数的终止条件。
步骤4 对种群进行选择、交叉、变异操作,重新计算适应值,保留最优,更新产生新一代种群Xn(i)。
步骤5 得到GA算法寻优的种群Xn(i)作为DE初始值Xm(0)。
步骤6 对齿轮系统的轻量化DE适应度函数2进行定义,重点考虑齿轮系统体积最小问题,获取更符合实际的优质解。
步骤7 判断是否满足DE种群最大进化代数的终止条件。
步骤8 对种群进行变异、交叉、选择操作,重新计算适应值,保留最优,更新产生新一代种群Xm(i)。
2 齿轮系统轻量化参数优化
二级齿轮系统轻量化的主要方式有:新型轻质材料替代、拓扑结构优化、结构参数优化[5]。本文采用结构参数优化,运用上节提出的GDE算法进行轻量化设计,最终得出优化后的齿轮系统参数。二级齿轮结构简图如图2所示,企业二级齿轮参数见表1。
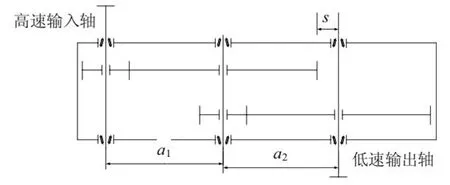
图2 二级齿轮结构简图
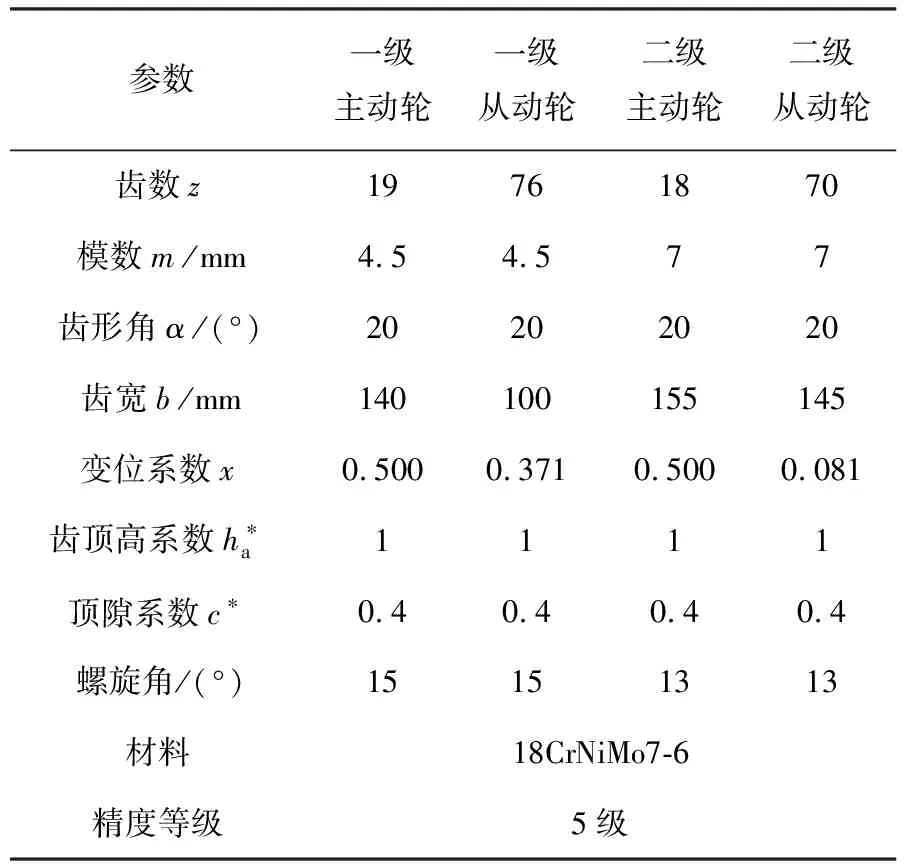
表1 企业二级齿轮系统参数
2.1 确定设计变量
由图2可知,齿轮二级系统轻量化的设计受齿轮基本参数的影响,齿轮系统质量与中心距和体积紧密关联,其轴向中心距尺寸由传动比和齿轮分度圆直径决定,齿轮系统的体积与齿宽系数以及齿根圆、齿顶圆有关。鉴于此,对齿轮相关设计变量的设计见表2。
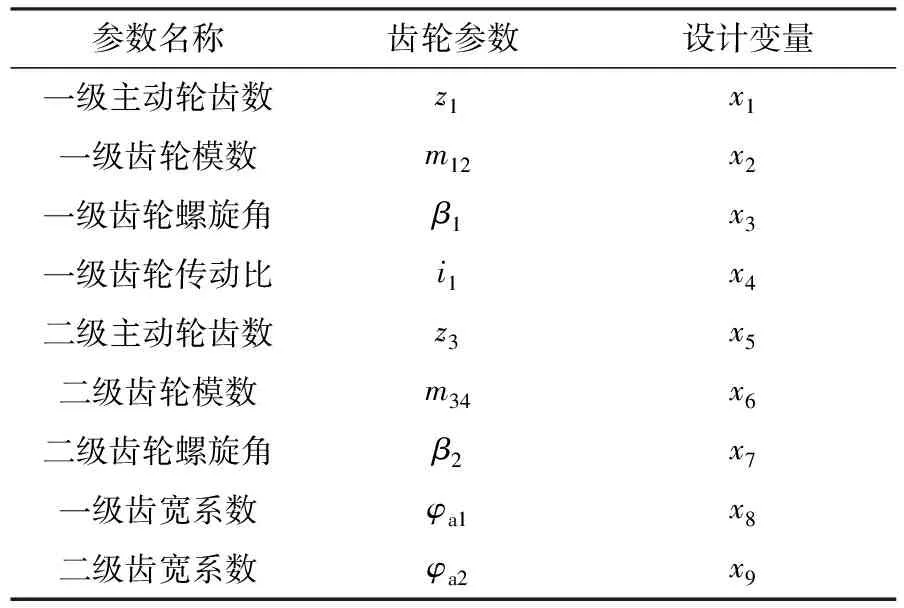
表2 二级齿轮系统轻量化设计变量
2.2 建立目标函数
齿轮二级系统的轻量化问题可以转化为如图2所示的中心距最小问题,即a1与a2和的最小值问题,表达式为
(1)
将目标函数1设置为
(2)
式中:i为齿轮系统总传动比,按照企业齿轮系统参数,可知i=15.4,将目标函数1用于GA中的适应度函数。
对二级齿轮系统的体积进行计算,采用分度圆法体积计算公式[6]为
(3)
式中B为轮齿宽度,且B=φa,φ为齿宽系数,a为中心距。将目标函数2设置为
(4)
2.3 确定约束函数
结合摩擦激励的相关影响因素,考虑齿宽、螺旋角等齿轮参数对齿面摩擦力的影响,在轻量化设计的同时对增大齿面摩擦力、增强摩擦激励的齿轮参数加以限制;同时在轻量化设计过程中还要保持原有齿轮的齿面疲劳强度、齿根弯曲强度、几何限制因素等特性。综上,对轻量化齿轮系统的约束函数设置如下:
1)螺旋角约束
(5)
2)传动比约束
(6)
3)齿宽系数约束
(7)
4)齿面接触疲劳强度约束
(8)
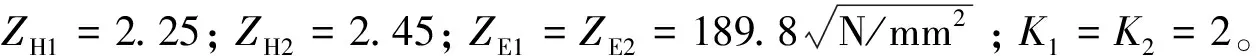
5)齿根弯曲疲劳强度约束
(9)
根据文献[8]可得:[σF1S]=[σF2S]=714 MPa;YFa1=2.76;YFa1′=YFa2′=2.22;YFa2=2.83;Yβ1=0.875;Yβ2=0.89;YSa1=1.56;YSa1′=YSa2′=1.77;YSa2=1.54。
6)不干涉相碰约束
(10)
7)不发生齿轮根切的约束
(11)
式中αn为斜齿轮法向压力角。
8)其他齿轮参数的约束
(12)
3 优化结果分析
对上述目标函数与约束函数进行MATLAB编程,分别运用DE、GA与编写的GDE算法程序进行优化设计和求解运算,圆整后得到的优化结果见表3。
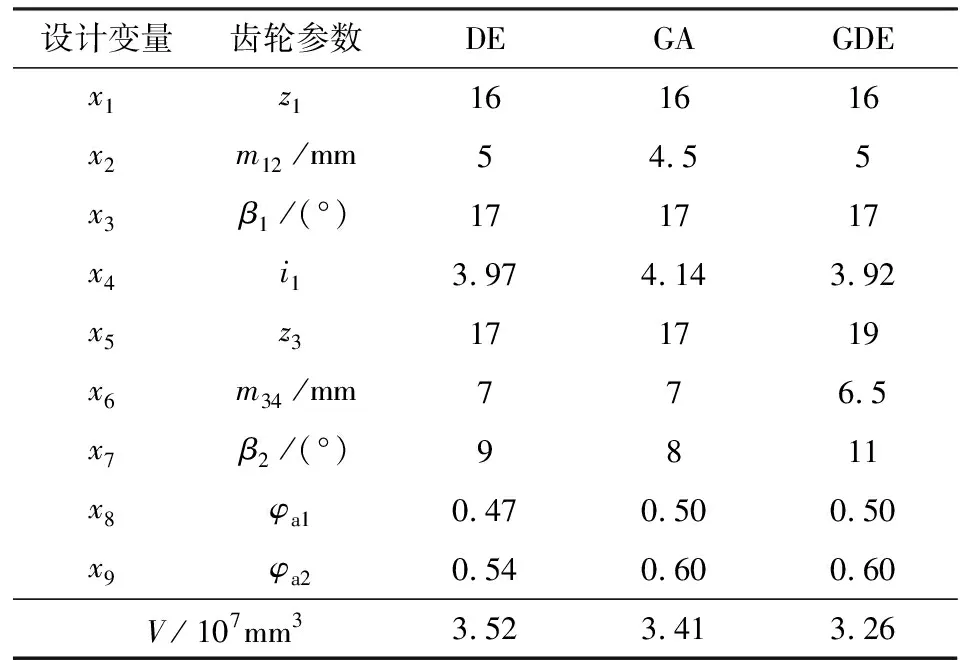
表3 各算法优化结果
3种优化算法的适应度函数、累积分布函数变化曲线如图3、图4所示。由图3可知,GA在约90代时找到了最优解,DE在约40代时找到了最优解,而GDE在约20代时找到了最优解;3种方法相比较,GDE收敛速度最快且运算效率高。由图4可知,GDE适应度函数有80%以上的解可以落到3.3×107mm3的值以内,GA适应度函数有60%以上的解可以落到3.4×107mm3的值以内,DE适应度函数有10%以上的解可以落到3.4×107mm3的值以内,说明DE容易陷入局部最优,而GA全局寻优能力强,GDE结合了两者优势,所得的解更优。
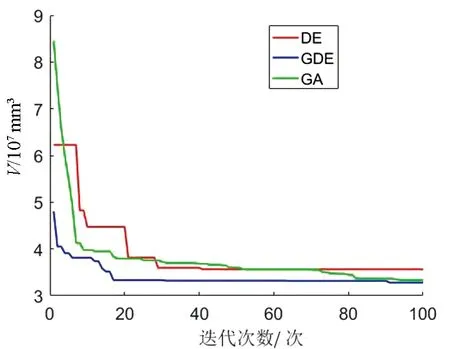
图3 3种优化算法的适应度函数变化曲线
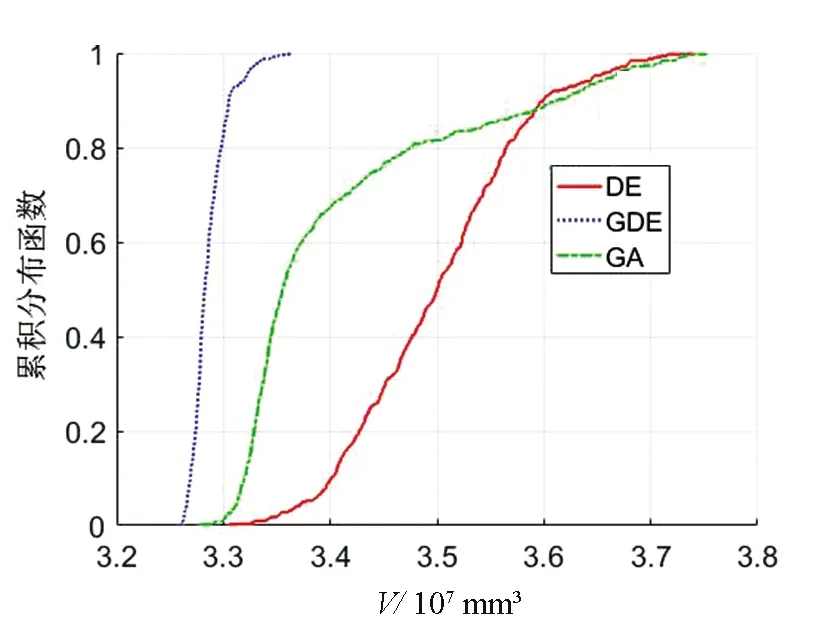
图4 3种优化算法累积分布函数变化曲线
将各优化算法与原齿轮系统体积和重合度进行对比可知,GA优化后齿轮体积减少了6.3%,重合度增加了2.1%;DE优化后齿轮体积减少了3.3%,重合度增加了1.5%;GDE优化后齿轮体积减少了10.5%,重合度增加了5.8%。相比较其他两种算法,GDE优化的结果更合理,效果更好。
4 模态分析
对优化后的齿轮系统进行模态分析,分析优化后固有频率和振型的变化以及轻量化齿轮系统的振动特点和优化效果。将优化后齿轮系统模型进行简化并导入Ansys Workbench软件中,在Modal模块中定义齿轮系统的几何属性、网格控制和圆柱约束[9],考虑该系统的大小和实际硬件设备,设置求解阶数为6阶,完成求解。
模态分析中,一般前6阶模态对系统的影响较大,因此本文主要针对系统前6阶的固有频率和振型进行分析。系统前6阶模态振型如图5所示,模态计算结果见表4。

(a)第1阶 (b)第2阶 (c)第3阶
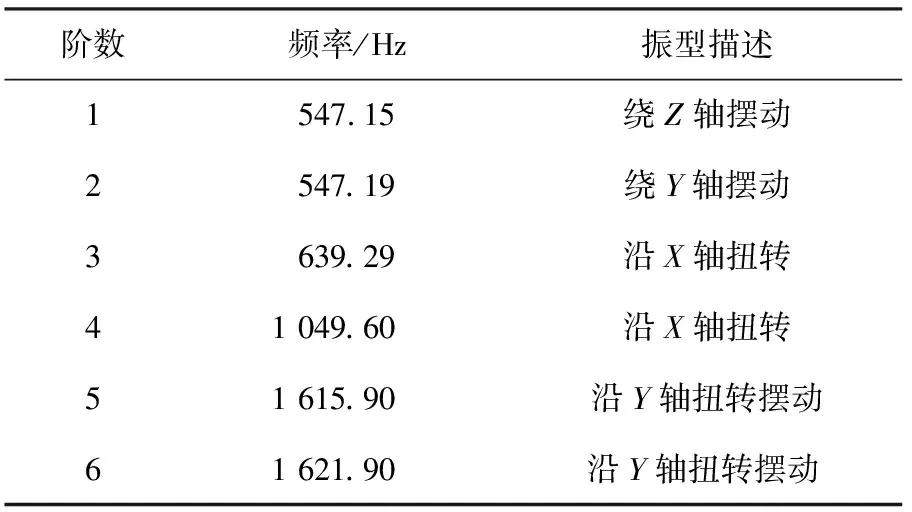
表4 优化齿轮系统前6阶模态计算结果
由表4可知,齿轮系统最大频率为1 621.90 Hz,最小频率为547.15 Hz。由齿轮啮合频率的计算公式可得二级齿轮啮合频率为293.38 Hz,三级齿轮啮合频率为69.49 Hz。对比可知,与箱体振动频率以及齿轮啮合频率均不重叠,不会产生共振,适用于实际工况。
5 结论
1)提出一种GDE混合算法,以两级齿轮系统中心距与体积最小为目标进行轻量化设计,所得结果与两种传统方法结果进行的比较显示,GDE收敛速度快,在20代左右即可找到最优解,GDE适应度函数有80%以上的解可以落到3.3×107mm3的值以内。
2)对GDE算法进行的编程仿真结果表明,GDE优化后齿轮体积减少了10.5%,重合度增加了5.8%。
3)对轻量化后齿轮系统进行建模和模态分析,仿真结果显示轻量化后齿轮不会产生共振,符合实际工况需求。
