基于聚类的半挂牵引车行驶工况构建改进方法

王保林，田瑛，袁俊凯，王黎明，周英超

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

行驶工况描述特定交通环境下车辆行驶特征，用于确定车辆燃油消耗量和污染物排放量，对于新车型的技术开发和评估具有重要意义[1-3]。目前，商用车行驶工况主要分为两大类：一类是立法工况，由政府制定，以实施油耗与排放认证,典型的有美国的NYCC、日本的JC08、世界重型商用车瞬态循环WTVC以及国内的C-WTVC[4]和CHTC行驶工况[5]等；另一类通过收集道路行车数据，结合加速、匀速、减速及怠速行驶状态，构建典型的城市或区域行驶工况。目前我国半挂牵引车主要采用CHTC-TT工况，但因不同地区之间环境气候、交通状况、道路条件的差异，CHTC-TT工况并不适用于所有城市或区域，因此有必要根据当地实际道路的车辆行驶数据，构建具有代表性的典型行驶工况。

近年来，国内外对行驶工况构建方法的研究主要有短行程法、聚类法及马尔可夫法。短行程法将车辆行驶数据划分为若干个运动学片段，提取出具有代表性的运动学片段进行工况构建。王国林等[6]通过短行程法分别构建了镇江市出租车和私家车行驶工况，其缺点在于受限于单个片段的长度，难以精确控制典型工况的时长。聚类方法基于主成分分析对选取的能反映车辆运行特征的部分参数进行分析，解析这些特征参数的主成分，再通过聚类分析，构建不同类型的行驶工况。胡宸等[7]利用主成分分析和K-均值聚类算法构建了哈尔滨城市公交工况，但聚类过程中最优聚类数K值事先确定，同时初始聚类中心随机选择，选择不好易收敛到局部最小值。马尔可夫法的核心思想是把汽车行驶过程中加速、减速、匀速和怠速4种状态看作4种模型，将一个完整的工况看作一个马尔可夫过程。Jiang等[8]利用马尔可夫法构建了城市车辆的驾驶周期，张昕等[9]利用一维马尔可夫链预测构建了混合动力汽车行驶工况。马尔可夫法拥有较高精度，但只能对整体数据进行分析，无法针对不同道路类型的行驶工况分别进行构建。综上所述，本文拟采用聚类法构建行驶工况，针对传统的K-均值聚类易陷入局部最优且最优聚类数K值难以确定的问题，提出一种基于主成分分析的高斯混合模型聚类方法避免局部最优的情况，并通过贝叶斯信息准则保证聚类数K值最优。本文以半挂牵引车为试验车辆，基于车载无线终端采集的行车数据，预处理后以速度为运动学片段划分标准，通过主成分分析和聚类分析对试验数据进行降维分类处理，构建具有代表性的半挂牵引车行驶工况。

1 数据采集与前期处理

1.1 数据采集

为使采集的数据能真实有效地反映丘陵地区道路行驶工况，根据丘陵地区道路多坡道的特点，选取淄博市博山-沂源S231路段作为测试道路，全长56 km，车辆行驶路线如图1所示。常用的数据采集方式有循环路线法、自主驾驶法、车辆跟踪法。由于本文已经规划好试验区域和试验线路，因此选取循环路线法，采集路线为博山-沂源S231路段，数据采集周期为30 d，连续不间断，具体时间段选定为每天7：00-11：30，14：00-18：30，19：00-23：30，包括早晚高峰期和交通空闲期。

图1 试验车辆行驶路线

试验车辆为青岛解放JH6重卡560马力6×4 AMT自动挡牵引车(国六)，数据采集设备采用车载CAN-BUS无线终端，该设备从CAN总线上不断采集试验车辆行驶过程中的数据，例如车速、发动机转速、海拔高度等，同时接收GPS定位，将设备的经纬度位置信息实时记录下来，通过上位机软件读取试验数据。设备共4个接口，分别与车内CAN总线和电源线连接，并安装在试验车辆的仪表盘上，如图2所示。采样频率选择1 Hz，即数据采集间隔为1 s，每秒采集一组数据，如果选取的采样频率小，采样间隔大，单位时间内采集数据少，无法真实反映出汽车行驶过程中速度的实际变化情况。

图2 实车安装图

1.2 数据前期处理

由于数据采集的密集程度、汽车振动等原因会使得试验数据出现信号波动、噪声明显等情况，所以在数据正式处理之前需要对数据进行降噪处理，剔除一些波动幅度较大和干扰性强的数据[10]。目前常用的降噪方法有中值滤波、滑动平均值滤波、限幅滤波和一阶惯性滤波等。本文采用一阶惯性滤波方法，将本次采样数值与上一次经滤波后的输出值相加权，得到有效的滤波值，对周期性干扰和波动频率较高的数据具有较好的抑制和平滑作用。

图3和图4为某段原始数据滤波前后效果。从图3中可以看出，滤波前原始速度数据曲线中存在许多“尖峰”数据，在滤波后，速度曲线变得更加平滑。图4中滤波加速度和原始数据在保持跟随趋势的同时，也能有效覆盖原始加速度数据的峰值，说明滤波效果较为理想。

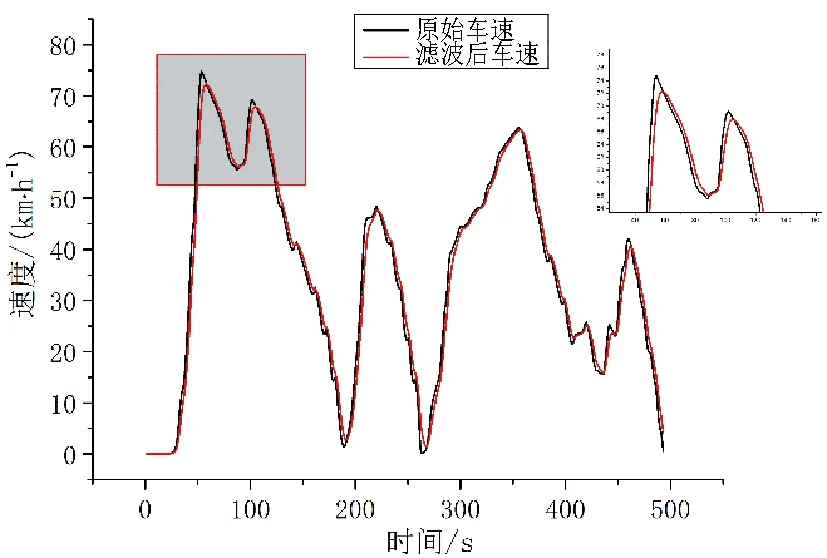
图3 滤波前后速度-时间曲线

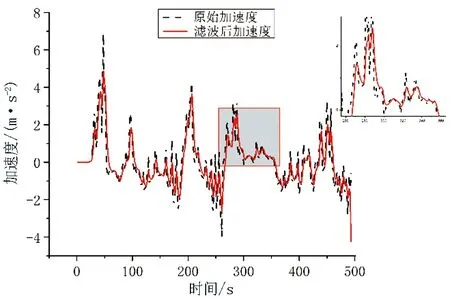
图4 滤波前后加速度-时间曲线

2 数据分析

2.1 运动学片段划分

在构建行驶工况过程中，选取速度作为运动学片段划分标准，将1个怠速开始到下1个怠速开始定义为1个运动学片段[11]，运动学片段示意如图5所示。

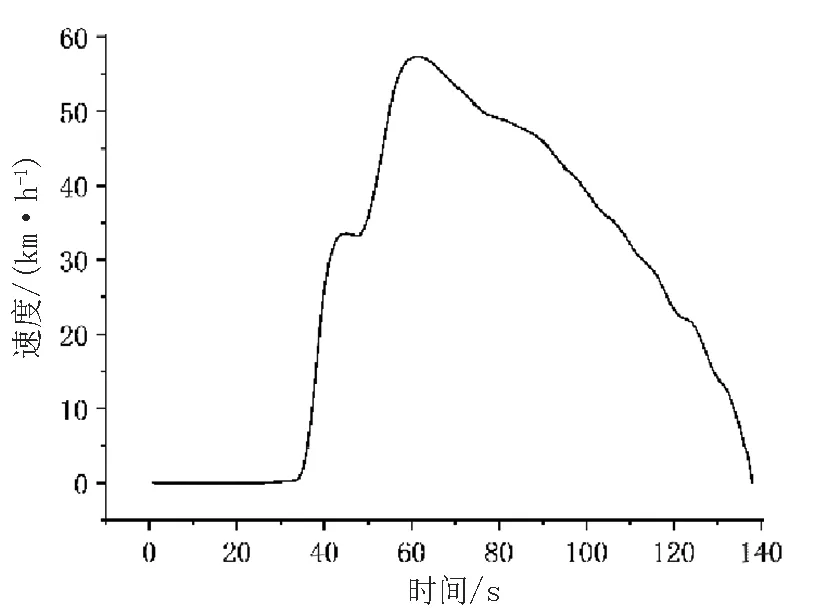
图5 运动学片段示意

汽车行驶过程可以看作多个加速、减速、匀速和怠速片段的组合。为详细反映运动学片段瞬时特征，按照速度v和加速度a将运动学片段状态划分为：加速状态(v>1 km/h且a>0.1 m/s2)、减速状态(v>1 km/h且a<-0.1 m/s2)、匀速状态(v>1 km/h且|a|≤0.1 m/s2)及怠速状态(v≤1 km/h且|a|≤0.1 m/s2)。

通过运动学分析，筛选出22个特征参数，主要参数见表1，其余分别为：加速工况时间比例Pj、减速工况时间比例Pd及匀速工况时间比例Py、怠速工况时间比例Pi、各速度区间所占时间比例P0-10、P10-20、P20-30、P30-40、P40-50、P50-60、P60-70、P≥70。

表1 主要特征参数及其含义

针对收集的历史行车数据，选取一个怠速开始到下一个怠速开始的运动学片段划分方法对行车数据进行划分，同时运动学片段筛选还需符合以下条件：运动学片段的持续时间不少于20 s；车辆加速度在0.1 m/s2≤a≤4 m/s2范围内，减速度在-4 m/s2≤a≤-0.1 m/s2范围内；一个运动学片段中必须包括加速过程与减速过程。

通过MATLAB软件对运动学片段划分，最终筛选了291个运动学片段，并计算其主要的10个特征参数，部分结果见表2。

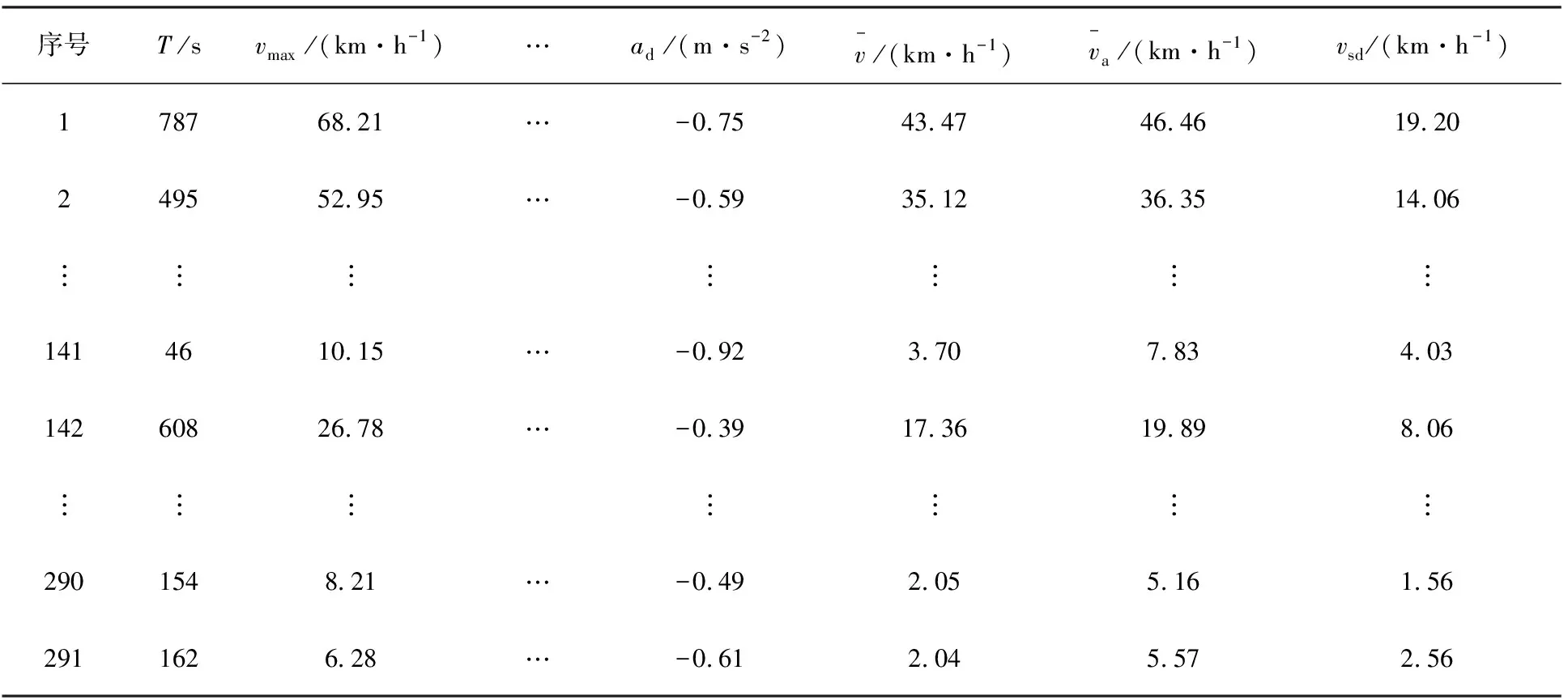
表2 运动学片段主要特征参数值

2.2 主成分分析

主成分分析是数据降维的一种常用方法，其特点是通过变量变换把注意力集中在具有较大变差的那些主成分上，舍弃那些变差小的主成分，将具有一定相关性的众多指标重新组合成几个少量互相无关的综合指标，同时最大程度地保持原有数据的信息。

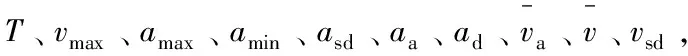
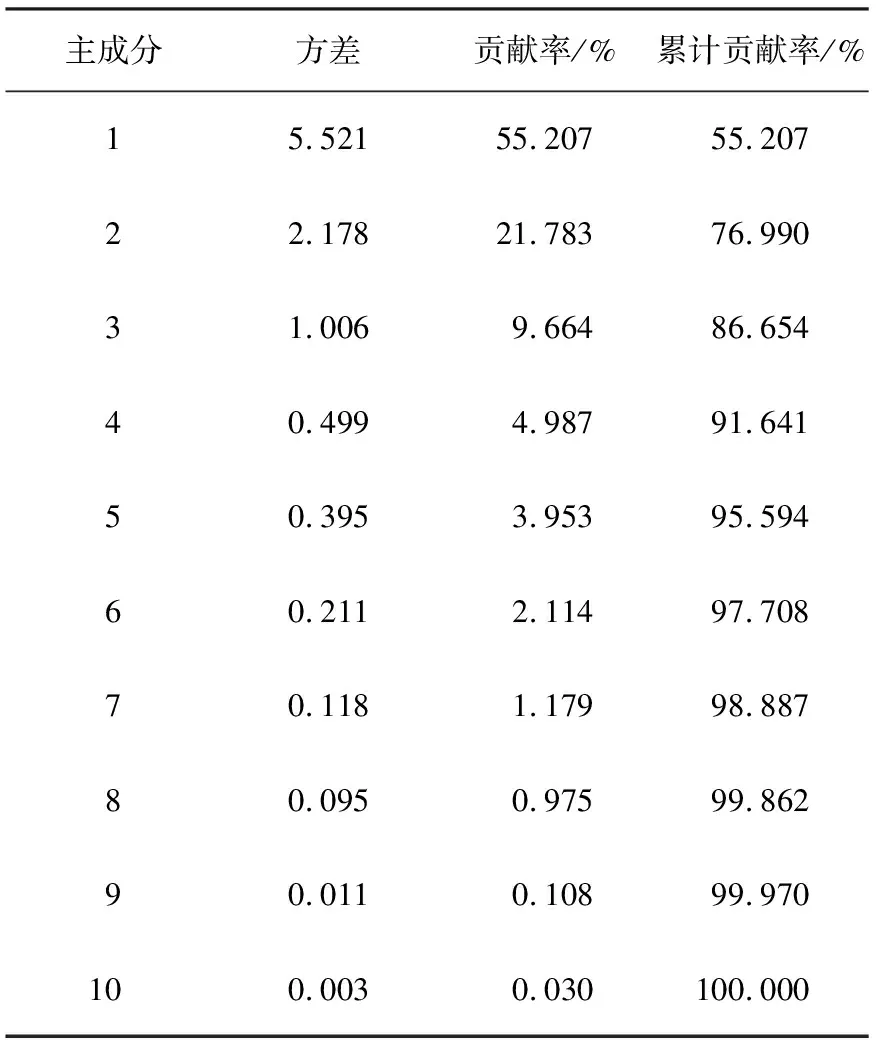
表3 主成分贡献率

表4是部分运动学片段的主成分得分，经过主成分分析后，将原有十维运动学片段特征参数矩阵简化为三维的主成分得分矩阵，在聚类分析中将对所有数据片段的主成分得分进行分类。

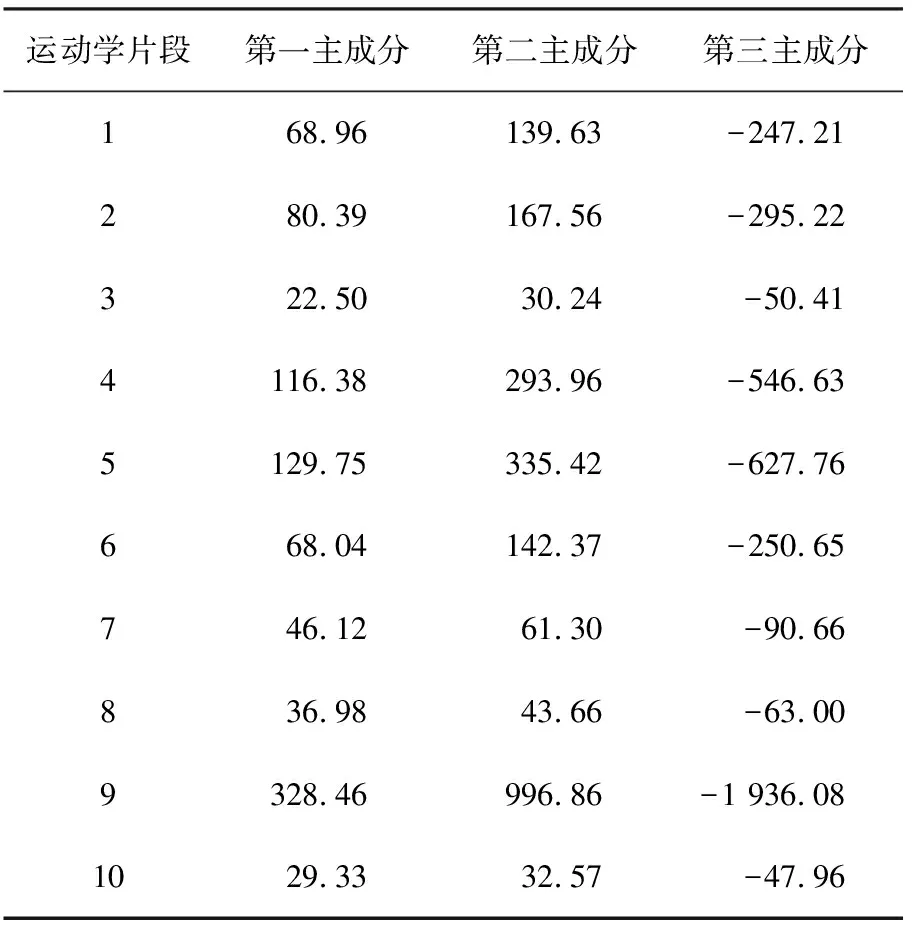
表4 特征值主成分得分

2.3 聚类分析及结果选择

常见的聚类分析有K-均值聚类、层次聚类、模糊聚类和高斯混合模型聚类等[13]。K-均值聚类的初始聚类中心随机选取，且最优聚类数K值难确定，而高斯混合模型聚类依据概率分配聚类成员，具有灵活的类簇形状，同时可以通过贝叶斯信息准则确定最佳聚类数K值。本文选取高斯混合模型聚类对主成分得分进行分类处理，高斯混合模型是多个基于高斯概率密度函数的混合模型，其原理为通过拟合输入数据集构建最合适的混合多维高斯分布模型。

2.3.1 高斯混合模型

假设n维随机变量x=(x1,x2,···,xd)T，包含k个子模型的高斯混合模型为

(1)

M(x|μk,∑k)=

(2)

(3)

式中：M(x|μk,∑k)为高斯概率密度函数；wk、μk、∑k分别为混合模型中第k个子模型的权重、均值、协方差矩阵；p(x)为高斯混合模型的概率密度函数。

2.3.2 似然函数

求出高斯混合模型生成的似然函数，因计算复杂往往对似然函数取对数，具体为

(4)

2.3.3 EM算法

对于高斯混合模型中的参数(wk、μk、∑k)，采用期望最大化算法(EM)进行求解。EM算法的基本思想是通过引入隐含变量，求解模型分布参数的极大似然估计，然后对隐含变量期望公式和模型分布参数重估公式进行反复迭代，直至似然函数值收敛[14]，其计算步骤分为E-step和M-step。

E-step：得到数据xi来自第k个子模型的概率

(5)

M-step：计算新一轮迭代的模型参数

(6)

重复计算E-step和M-step直至收敛。

2.3.4 最佳聚类数确定

本文选用贝叶斯信息准则(Bayesian information criterion，BIC)，即具有最低BIC值的模型对应的K值为高斯混合模型聚类的最佳聚类数，计算公式为

BIC=kln(n)-2ln(L)，

(7)

式中：k为模型参数个数；n为样本数量；L为似然函数。

计算不同聚类数值下的BIC值，结果如图6所示，当聚为3类时，BIC值最小，因此最佳聚类数为3。相较传统的K-均值聚类算法最佳聚类数难以确定的问题，本文采用贝叶斯信息准则确定最优聚类数，提高了行驶工况构建的精度。

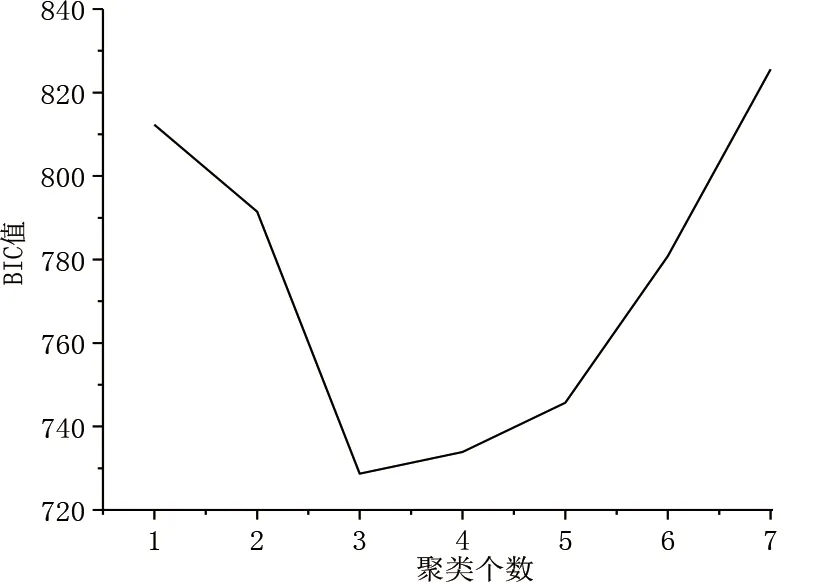
图6 不同聚类个数下的BIC值

运用MATLAB软件对主成分得分进行高斯混合模型聚类，其聚类效果如图7所示，不同聚类的样本采用不同颜色表示。

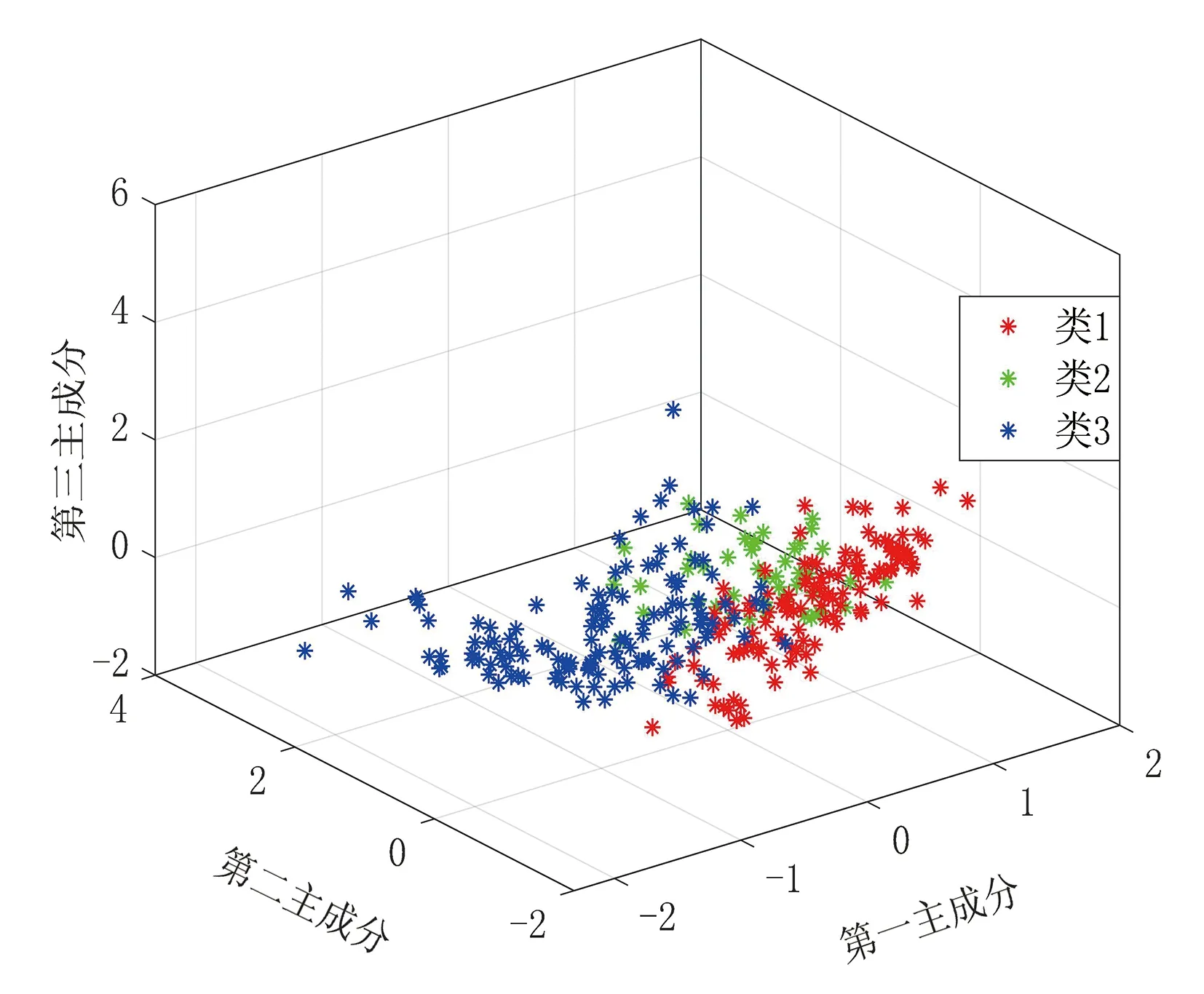
图7 运动片段聚类效果图

对分为3类时各片段类型速度段和行驶状态所占的时间比例进行统计，结果如图8所示。从图8可以看出，聚类结果第1类为低速类，0～10 km/h速度占比为80.52%，怠速比例达到44.85%；第2类为中速类，速度区间主要集中在20～50 km/h，匀速比例达到27.73%；第3段为高速段，60～70 km/h速度占比为47.82%，加速和减速所占比例较高，加减速情况较频繁。

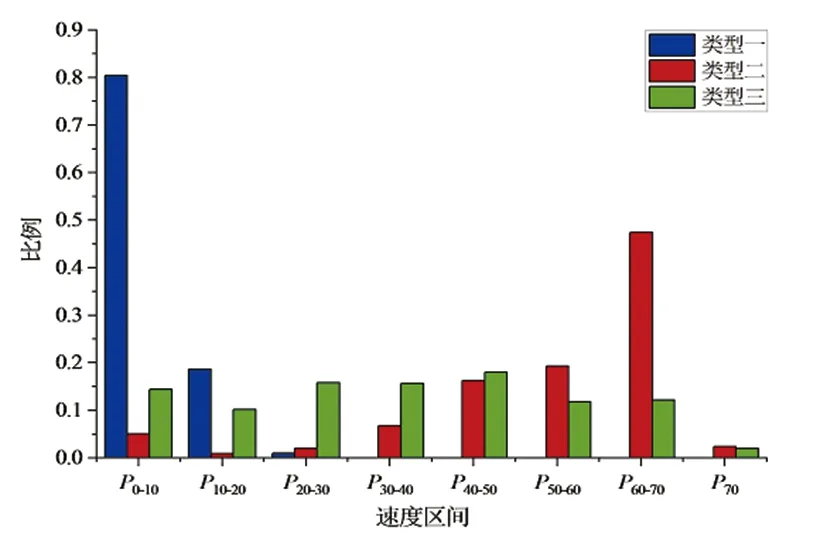
(a)速度段占比

3 行驶工况的构建

3.1 工况合成方法

根据聚类分析结果，得出各分类中所包含的运动学片段与其聚类中心的距离dij大小，当距离越小时，运动学片段的相关系数rij越大，说明该运动学片段越能反映该类中的行驶特点。因此，本文通过聚类分析时运动学片段与其聚类中心的距离dij，从中选取3个各类型中dij最小的片段，即相关系数rij最大的3个运动学片段，按照低速-中速-低速-高速的顺序随机排列组合，合成≥1 200 s的丘陵山区半挂牵引车候选行驶工况。

3.2 行驶工况的确定

对于速度行驶工况，本文将平均速度、速度标准差、加速度标准差、加速工况时间占比、减速工况时间占比、匀速工况时间占比、怠速工况时间占比7项作为主要筛选参数。

为了选择最具代表性的行驶工况，把相对误差(RE)、性能值(PV)和速度-加速度概率分布(SAPD)作为决策标准[15]。首先，计算候选行驶工况的评估参数与真实试验数据之间的RE。如果每个评估参数的RE都小于10%，则可以接受候选的行驶工况。然后计算PV，选择PV最小的候选行驶工况。

(8)

式中:θc为候选驾驶周期的评估参数值；θt为原始试验数据的评估参数值。

(9)

式中：REi为第i个评估参数的RE；n为评价参数的数量。

3.3 速度工况合成结果分析

根据上述工况合成方法和筛选标准，通过MATLAB软件合成如图9所示的具有代表性的丘陵山区半挂牵引车行驶工况，共计1 210 s，所构工况和实际工况的SAPD如图10和图11所示。

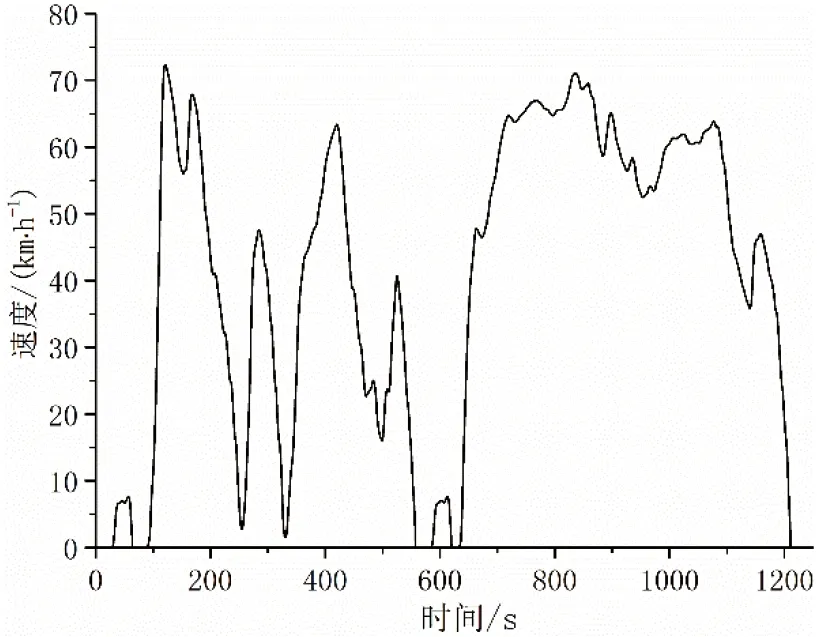
图9 半挂牵引车行驶工况的速度-时间曲线

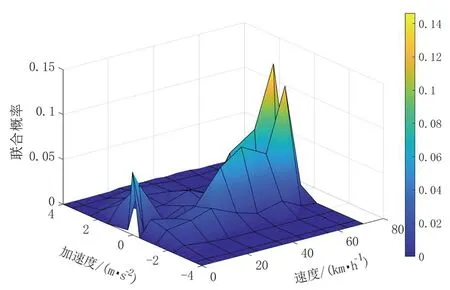
图10 所构行驶工况的SAPD分布图

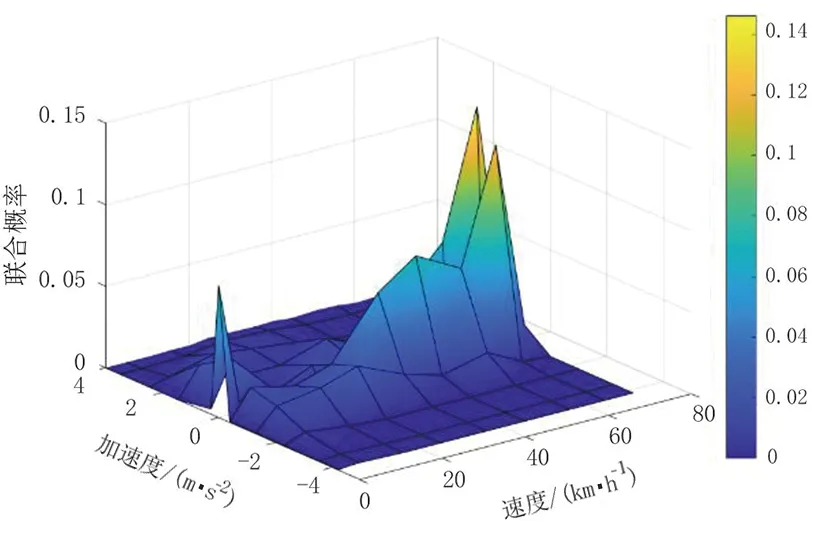
图11 实际工况的SAPD分布图

将基于传统K-均值、高斯混合模型构建的车辆行驶工况同实际工况进行对比，各工况的特征参数见表5。由表5可知，基于高斯混合模型构建的车辆行驶工况与实际工况主要特征参数的相对误差都保持在5%以内，性能值为2.05%；而基于传统K-均值构建的车辆行驶工况与实际工况的匀速时间比例相对误差为9.09%，性能值为4.50%，明显高于基于高斯混合模型构建的车辆行驶工况同实际工况的相对误差。以上分析表明，传统K-均值聚类构建的工况由于初始聚类中心随机选取，导致构建工况陷入局部最优，与实际工况误差较大；而基于高斯混合模型聚类构建的丘陵山区半挂牵引车行驶工况特征参数与实际工况相比误差更小，且车速变化更符合实际情况，更能反映丘陵山区道路线形复杂的特点。

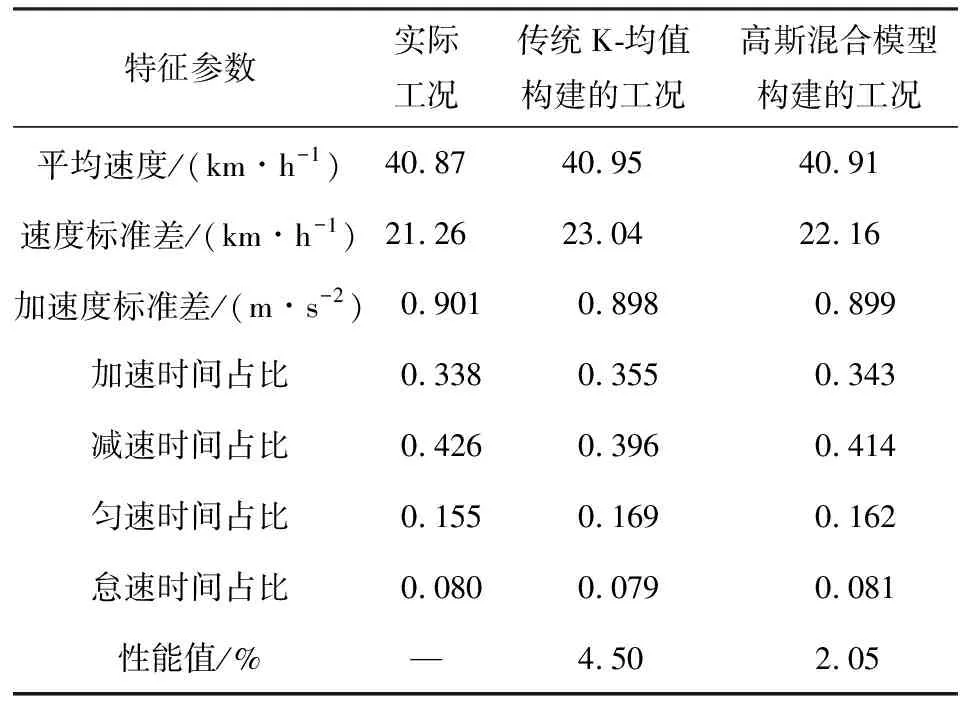
表5 各工况下的评价参数

将本文构建的丘陵山区半挂牵引车行驶工况同中国重型半挂牵引车行驶工况(CHTC-TT)进行比较，结果见表6。与CHTC-TT工况相比，构建的半挂牵引车工况由于丘陵山区道路线形复杂的特点，车辆行驶过程中平均速度、匀速比例分别降低了11.91%、72.20%，加速段平均加速度、减速面平均减速度、加速比例及减速比例分别提高了171.43%、91.67%、96.79%，怠速比例同CHTC-TT工况接近。由此可见，CHTC-TT工况不适用于丘陵山区半挂牵引车行驶特征，表明开发反映丘陵山区行驶特征的半挂牵引车实际行驶工况具有重要意义。

表6 丘陵山区半挂牵引车行驶工况与其他半挂牵引车典型工况对比

4 结论

1)以半挂牵引车为研究对象，划分运动学片段，采用主成分分析和高斯混合模型聚类算法对原始数据进行降维分类处理，构建出了符合丘陵山区半挂牵引车实际行驶特征、时长1 210 s的丘陵山区半挂牵引车行驶工况。

2)与传统的K-均值聚类算法相比，基于高斯混合模型构建的车辆行驶工况的性能值仅为2.05%，精度更高。构建的丘陵山区半挂牵引车行驶工况同CHTC-TT工况进行比较发现，由于丘陵山区道路线形复杂的特点，特征参数存在较大差异，平均速度、匀速比例分别降低了11.91%、72.20%，加速段平均加速度、减速度平均减速度、加速比例及减速比例分别提高了171.43%、91.67%、96.79%，怠速比例同CHTC-TT工况接近。因此，采用CHTC-TT工况进行燃油排放标准并不能真实反映丘陵山区的交通状况，表明开发反映丘陵山区行驶特征的半挂牵引车实际行驶工况具有重要意义。

3)基于实车行驶数据合成的丘陵山区半挂牵引车行驶工况，总结丘陵地区半挂牵引车辆运行特征，可以有效模拟对应车辆历史行驶工况的统计学特性和概率分布特性，为半挂牵引车动力系统匹配及控制策略优化提供一定依据。