联合作战中航空兵作战规划研究

常一哲，李战武，江洋溢，罗振宇，鞠 明，赵刚练

（1.解放军93184 部队，北京 100076；2.空军工程大学航空工程学院，西安 710038；3.解放军93131 部队，北京 100089）

0 引言

联合作战是一个多军种参与、多任务交联、多平台协同的复杂过程，具有要素多、组织难、强度大等特点。航空兵作为联合作战的重要组成部分，担负了侦察搜索、火力打击、夺取制空权等多项任务。在此条件下，作战规划的质量影响到平台出动效率、任务完成效率、指挥协同效率等多项关键因素乃至最终的作战结果，因此，联合作战中航空兵作战规划是一个极具研究意义的问题。

现有研究成果主要分为作战建模思想和具体问题求解两类。作战建模思想类研究以定性描述联合作战的建模方法、体系架构为主，其中刘兆鹏以战役级联合作战方案的推演分析为研究对象［1］，设计了以任务- 指令为核心的联合作战方案概念模型，杜正军构建了基于态势、敌我双方行动、资源约束的序贯博弈模型［2］，樊青云提出了一种基于可扩展标记语言（extensible markup language，XML）的作战计划形式化描述方法［3］，设计了基于XMLSchema的作战计划形式化描述结构图，钱猛基于系统建模语言（system modeling language，SysML）研究了军事任务计划形式化描述与建模方法［4］，该方法考虑了作战行动序列元模型以及作战意图实体，MOFFAT J基于复杂性理论提出了战争复杂性的概念［5］，并建立了基于复杂性、知识与冲突的战争数学模型，CARES J R提出了信息时代作战模型［6］，该模型将作战单元分为传感器（Sensor）、决策者（Decider）、执行者（Influencer）与目标（Target）4 类，采用Perron-Frob-enius 特征值（PFE）度量作战效能；具体问题求解类研究多针对特定作战背景下的兵力规划具体问题展开，其中LEVCHUK G M 针对联合登陆战役中的任务-资源规划问题［7］，提出了多维动态列规划 算 法（multidimensional dynamic list scheduling，MDLS），阳东升对多兵种联合作战战役计划问题进行了数学描述［8］，并提出了多优先级列表动态规划算法（multi-pri list dynamic scheduling，MPLDS），鲁音隆提出了任务—平台双向选择的改进型多维动态列表规划算法［9］，缩短了任务完成时间，提高了资源利用率。包卫东提出了基于MDLS 和遗传算法（genetic algorithm，GA）的作战资源分配算法［10］，提高了任务分配的效率，并更好地实现了全局优化。

在以上研究基础上，本文提出了一种联合作战中航空兵作战规划方法。分析了联合作战中航空兵担负的典型任务及其逻辑时序，并构建了作战任务网络；其次从目标函数、约束条件和达到时间3 个角度建立了作战规划模型；再次基于PSO 研究了规划模型的求解算法，重点改进了个体编码方式和搜索策略；最后采用具体案例，对本文所提方法进行了仿真验证。

1 作战任务网络

刘兆鹏指出，作战任务是联合作战的基本组成单位，各任务依托相互关系形成任务网络，进而构成联合作战流程［1］。RAPOSO A B 给出了以时间序列（区间）为刻度的任务相互关系［11］，具体分为7种，分别是A equals B，A starts B，A finishes B，A meets B，A overlaps B，A during B，A before B，本文将任务A、B 的时间定义为［SA，EA］和［SB，EB］，得到任务相互关系描述如表1 所示。

表1 任务相互关系Table 1 Tasks interrelation

基于任务相互关系，结合航空兵典型使用特点，给出联合作战中航空兵作战任务网络，如图1 所示。

图1 联合作战中航空兵作战任务网络Fig.1 Tasks network regarding air force during joint operations

2 规划模型

图1 联合作战中航空兵作战任务网络描述的任务关系是逻辑时序关系，而非真实时序关系，两个任务的并行关系也指的是逻辑并行。例如在任务网络中反辐射打击和空战是并行关系，只是说在时序关系上可以在某一时间段内同步展开、协同进行，而非在任务开始和结束时刻上保持严格一致。

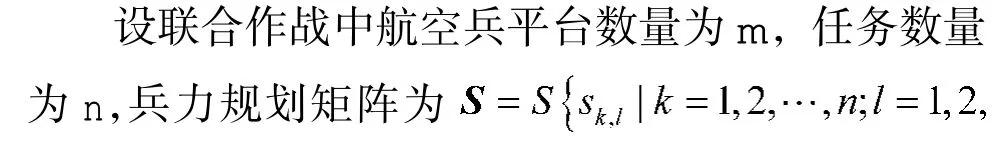
式（1）中，S 的元素值是平台编号，如sk，l是任务k 中第l 个平台的编号，缺省位置零。

2.1 目标函数

对于兵力规划问题，基于总任务时间最小进行考虑，因此，其求解目标属于最小最大化任务时间问题，具体数学模型为：

2.2 约束条件

2.2.1 平台约束

平台约束分为单平台约束和总平台约束，单平台约束是指单平台同一时间最多承担一项任务，总平台约束是指作战进程中所有平台总共承担至少一项任务，如式（5）所示：号；mpi是平台i 的执行任务次数。

任务协同时间约束是保证任务平台在时间上的协同，即多平台在同一时间窗口内协同执行任务，如式（7）所示：

任务关系时间约束是某一具体作战任务中，多子任务在保证任务开始时间协同的基础上，在执行顺序上的时间约束，例如在突防突击任务中，突击编队中的干扰机在随队支援干扰中应全程保证对威胁目标的压制，确保歼轰机完成对预定目标的打击及安全撤离，故干扰机的任务时间应大于歼轰机的任务时间。任务关系时间约束的表达如式（8）所示：

2.3 达到时间

到达时间是从平台i 从本场到任务k 区域单程所需时间，考虑到高度对航程影响较小，因此本文暂且忽略。以本场和任务区域为航路规划起点和终点，平台以巡航速度飞行，给出其模型如式（9）所示：

3 求解算法

航空兵规划作为兵力规划的一类具体应用，属于NP-hard 问题［12］。该问题的求解算法分为精确算法和启发式算法。精确算法在求解时效性方面存在严重缺陷，因此，业内的研究多集中于启发式算法。在启发式算法中，粒子群算法具有原理简单、实现容易、鲁棒性好的优异性能，但其主要用于求解连续空间函数优化问题，而航空兵作战规划问题属于离散空间函数优化范畴，为此必须作出针对性改进。本文重点从编码方式和搜索策略两方面进行研究。

3.1 解个体编码方式

离散空间优化问题解个体的编码方式有直接编码和间接编码两种，直接编码将任务方案作为解个体，间接编码则将平台与任务的分配处理规则作为解个体。考虑到航空兵规划问题的具体特征，其与普通的调度问题并不相同，主要体现在：1）任务组成单一，一个任务通常只有一道程序，不存在多道程序；2）任务分工具体，一个任务根据任务性质确定平台，而非需要所有平台参与；3）任务顺序明确，在完整的联合作战中航空兵的任务顺序是相对固定的，而非随机排列。根据以上特点，本文采用基于任务顺序的直接编码方式。具体思路为：假设联合作战中空中作战平台数量为m，任务数量为n，则解个体由平台按照任务顺序排列而成，其解个体编码的具体描述为：

图2 中个体编码的位数即全部任务的平台数量根据兵力需求矩阵确定，个体编码值则按照对应的平台类型集合排序确定。举例说明，假设参战兵力中有8 架歼击机，任务三的兵力需求中包含4 架歼击机，这4 架歼击机的编码位数为6～9，则其个体编码可以描述为：

图2 个体编码示意图Fig.2 Skematic diagram on individual coding

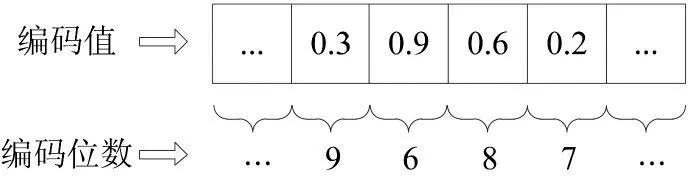
根据编码值进行排列，个体编码变为：

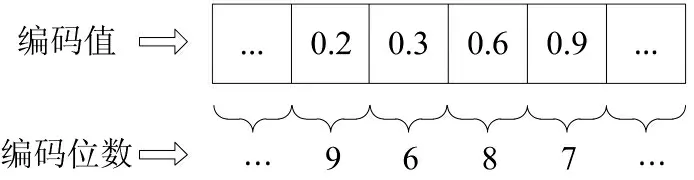
将编码值映射到兵力需求矩阵中，得到个体编码为：

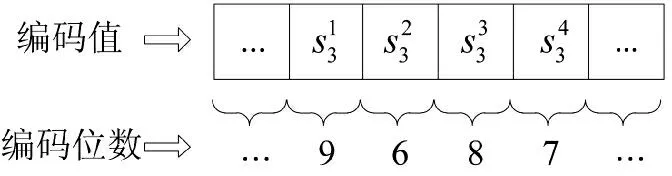
按照编码位数调整，形成最终个体编码：

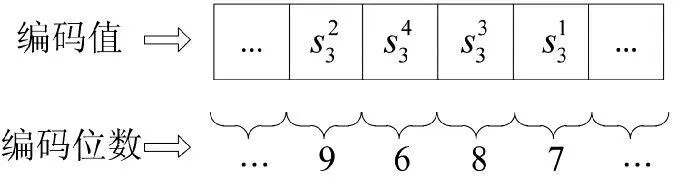
经过以上转换，粒子群个体中的编码值与兵力需求矩阵中的平台编号实现了对应。

3.2 搜索策略改进

3.2.1 淘汰与克隆机制

为防止粒子群趋于同质化引起的种群多样性水平降低，本文在算法中引入淘汰与克隆机制。在每完成一次迭代后，对更新后的粒子个体依据适应度高低进行排序，选择适应度较低的粒子个体进行淘汰，同时选择适应度较高的个体进行克隆，淘汰和克隆的个体数相等，如此保证在确保群体规模不发生变化的同时提升整个群体的适应度水平，具体如图3 所示。

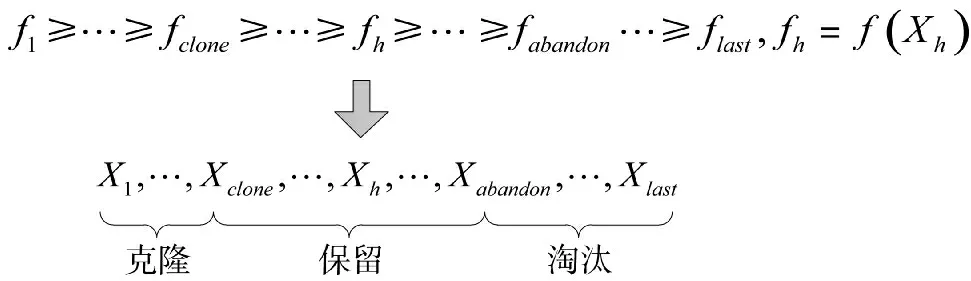
图3 淘汰与克隆机制示意图Fig.3 Schematic diagram on individual eliminating and coloning mechanism

图3 中Xh是粒子群中的个体h；Xclone是粒子群中进行克隆的最后一个个体；Xabandon是粒子群中进行克隆的第一个个体；fh是粒子个体h 的适应度值。

3.2.2 高斯扰动策略

针对PSO 算法易早熟的问题，本文引入高斯扰动策略，通过在速度更新模型中增加高斯局部扰动项，对粒子个体的搜索速度进行干扰，增加跳出局部最优的概率，达到避免早熟的目的。增加高斯局部扰动项的速度更新模型如式（10）所示：

ωu是u 次迭代的惯性权重，其模型为：

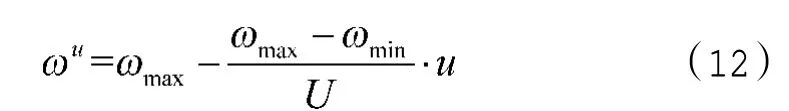
式（12）中，ωmax为惯性权重的最大值；ωmin是惯性权重的最小值；U 代表最大迭代次数。

3.3 求解算法流程

依据上述改进，给出改进PSO 流程，如图4 所示。

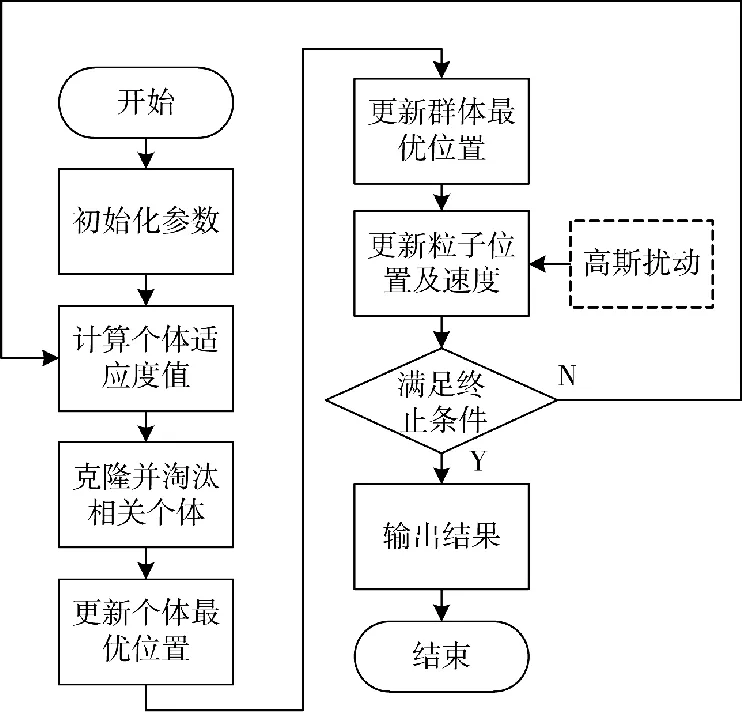
图4 改进PSO 流程Fig.4 Flow chart of improved PSO

4 仿真分析

以联合作战中航空兵使用为例进行研究，假设在作战中航空兵相关信息如表2～表3 所示。

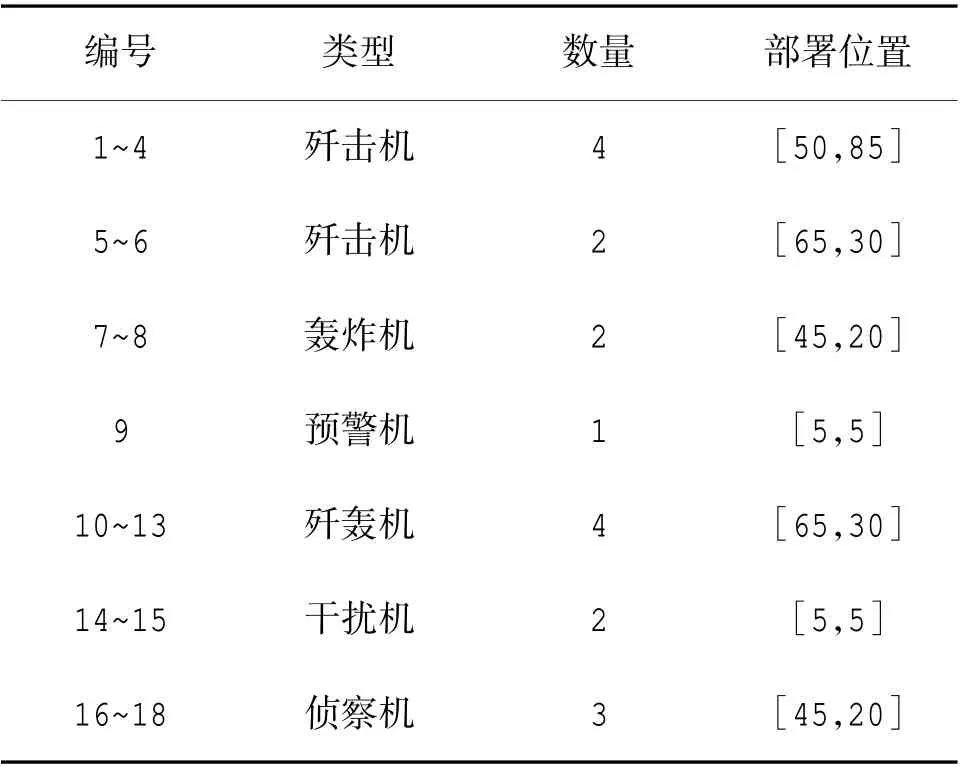
表2 航空兵类型及部署位置Table 2 Types and deployment location

表3 任务区域及平台需求Table 3 Tasks regions and requirements for units

从图5～图6 中可以看出，在两种不同算法得到任务时序图中，基于改进PSO 计算得到的作战任务规划总时间，相比标准PSO 计算得到的结果少用了3 min。从作战规划整体来看，优化结果仅产生了小幅度提升，对其原因进行分析，主要是问题的求解规模相对小且对任务顺序进行了约束，导致解的搜索空间较小，优化效果不明显。尽管如此，优化结果仍证明了本文所提方法的有效性。同时，改进PSO优化得到的任务规划方案满足规划模型中的约束条件，证明了本文所提方法的可行性。为进一步分析求解算法的性能，图7 给出了本文所提出的改进PSO 与标准PSO 的寻优过程。

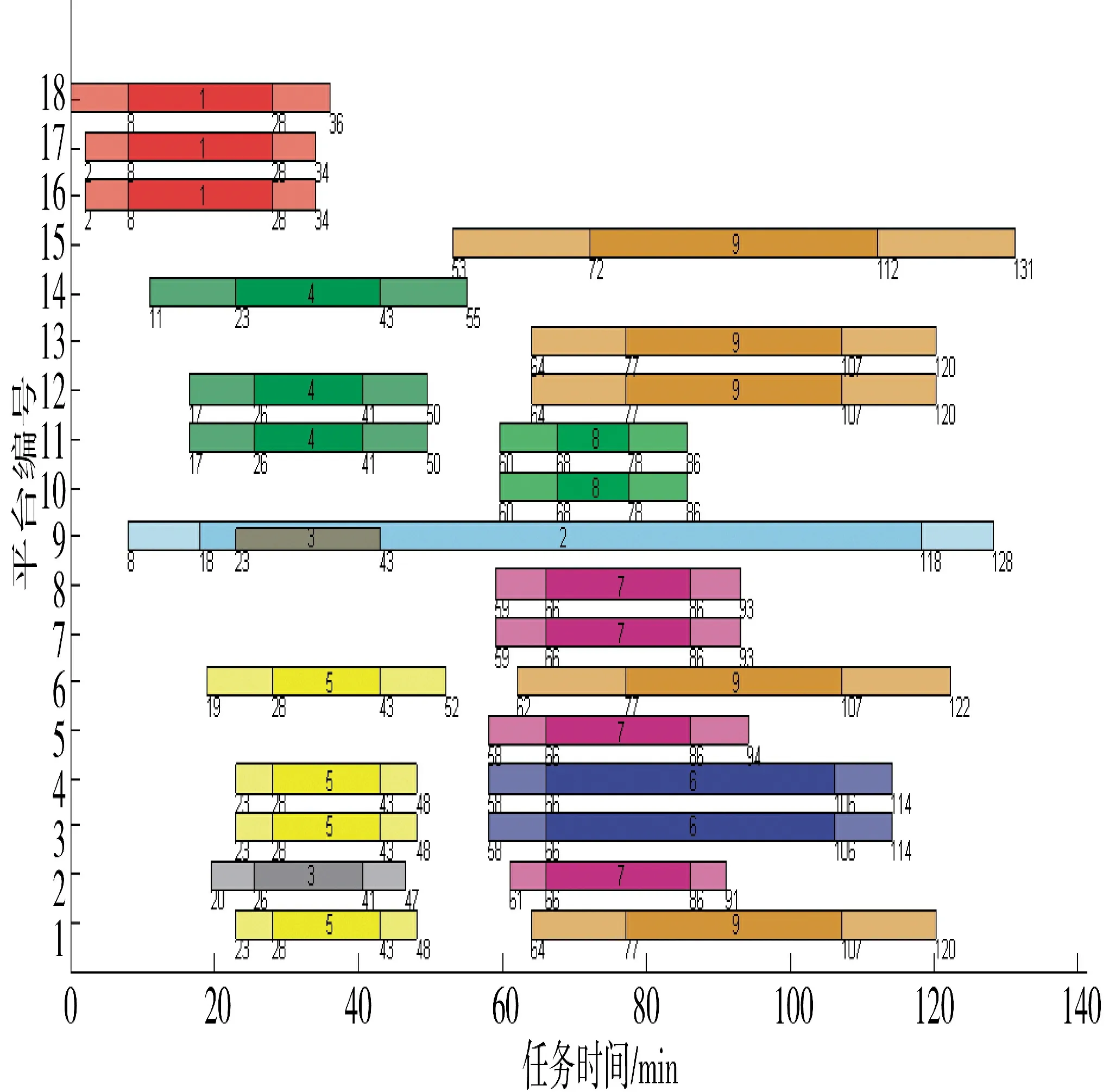
图5 基于标准PSO 算法得到的任务时序图Fig.5 Gantt chart based on standard PSO algorithm

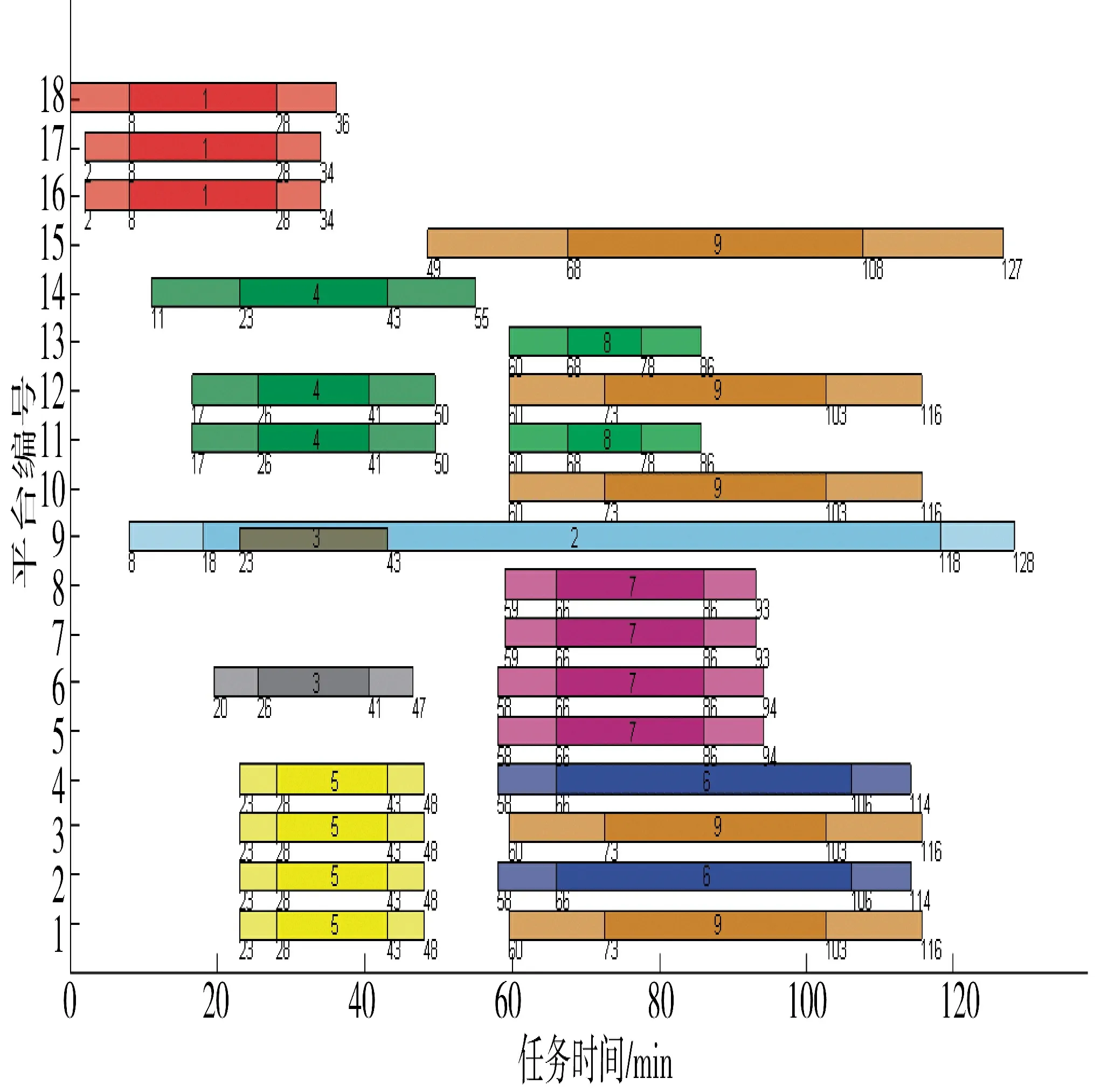
图6 基于改进PSO 算法得到的任务时序图Fig.6 Gantt chart based on improved PSO algorithm

从图7 中可以看出，标准PSO 在搜索过程中收敛速度相对快，然而其所得到的解的质量较差，产生了早熟的现象。作为对比，改进PSO 收敛速度慢，但是解的质量优于标准PSO，证明了本文引入的淘汰克隆机制和高斯扰动策略改进了PSO 的缺陷，有效避免了早熟。最后，根据求解结果，利用二维位置坐标对航空兵作战规划方案进行可视化描述，如图8 所示。

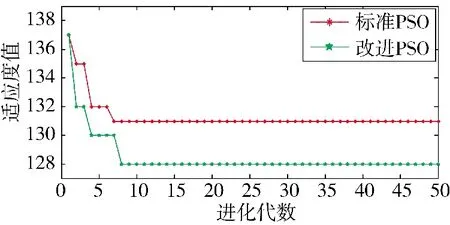
图7 两种算法寻优过程对比Fig.7 Comparison of optimization process of two algorithms

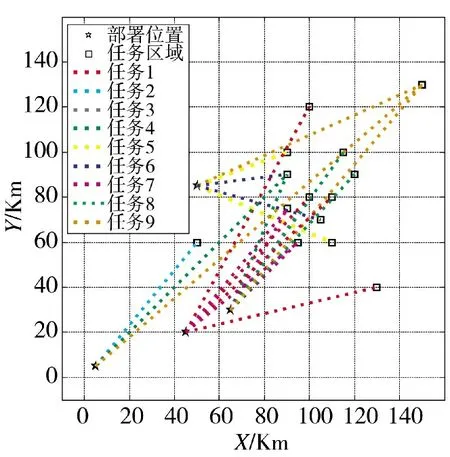
图8 基于二维位置坐标的航空兵作战规划方案Fig.8 Operational plan scheme on two-dimension coordinates of army air

5 结论

本文研究了联合作战中的航空兵作战规划问题并对应提出了一种规划方法。首先研究了联合作战中航空兵的主要作战任务及其逻辑关系与时序，并构建了作战任务网络；其次基于作战任务网络，建立了关于目标函数、约束条件以及到达时间的规划模型；再次以粒子群算法（PSO）为基础，从编码方式、搜索策略等方面进行了改进，并将其应用至规划模型的求解中；最后通过算例仿真的方式进行验证，结果验证了本文所提方法的可行性和有效性。

在后续工作中，将重点关注如将目标毁伤效果引入研究中，从联合作战动态特性的角度入手，更全面、更真实、更深入地对航空兵作战规划问题进行描述和求解。