通航训练机场跑道容量评估模型设计仿真
2023-03-11王汝昕
王汝昕,康 瑞
(1. 中国民用航空飞行学院机场工程与运输管理学院,四川 广汉 618307;2. 中国民用航空飞行学院空中交通管理学院,四川 广汉 618307)
1 引言
近年来,通用航空迎来快速发展阶段。截至2020年,飞行培训小时数占通用航空作业总量超过60%,如何在满足安全训练的条件下提高训练效率,成为民航培训部门关注焦点。跑道容量是衡量训练飞行效率的重要指标,也是制定训练计划的重要依据。国内外学者已在此领域进行了大量研究。Bowen等首次提出只有达到航空器的单跑道容量评估模型[1],随后Blumstein等对此模型进行改进[2];Harris等考虑导航设备和人为因素,建立基于随机因素的跑道容量评估模型[3];lee等考虑通信延迟和天气等因素,提出了机场容量和延迟模型,应用于美国多个机场[4];胡明华等利用概率与数理统计分析方法建立了单跑道容量评估模型,并对虹桥机场容量进行仿真计算[5];孟祥伟等人综合三种模型特征,提出了单跑道容量评估模型并验证不同建模逻辑模对跑道容量的影响[6];王莉莉等在相关平行仪表进近条件下,使用SIMMOD仿真软件对首都机场跑道容量进行仿真评估[7]。
以上模型主要适用于枢纽或干线机场,此类机场跑道和滑行道结构(以下简称跑滑结构)完整,航空器使用跑道滑行时间短且尾流等级和进近类别较高,管制和尾流间隔是限制跑道容量的关键因素。而飞行训练的机场多为通用或支线机场,跑滑结构简单,滑行时间是影响跑道容量的关键因素。康瑞等考虑跑滑结构对跑道占用时间的影响,提出了民航支线机场的容量评估模型[8],但该模型主要针对运输飞行航空器,并未考虑通航训练飞行科目对跑道容量的影响。
本文在满足相关管制安全间隔要求的基础上,充分考虑通用机场跑滑结构和训练飞行跑道运行规则,对起飞、全停和落地连续过程进行抽象,在不同起降比、全停和落地连续比下,计算航空器起飞、全停和落地连续跑道占用时间。采用VC++和Matlab编程实现模型,并进行数值模拟仿真,就相关参数变化对跑道容量影响进行分析,结合训练科目、飞行训练操作、天气和跑道条件等对提高机场跑道容量进行讨论。
2 训练飞行航空器跑道运行规则
训练飞行航空器使用跑道方式一般包括起飞、全停和落地连续。


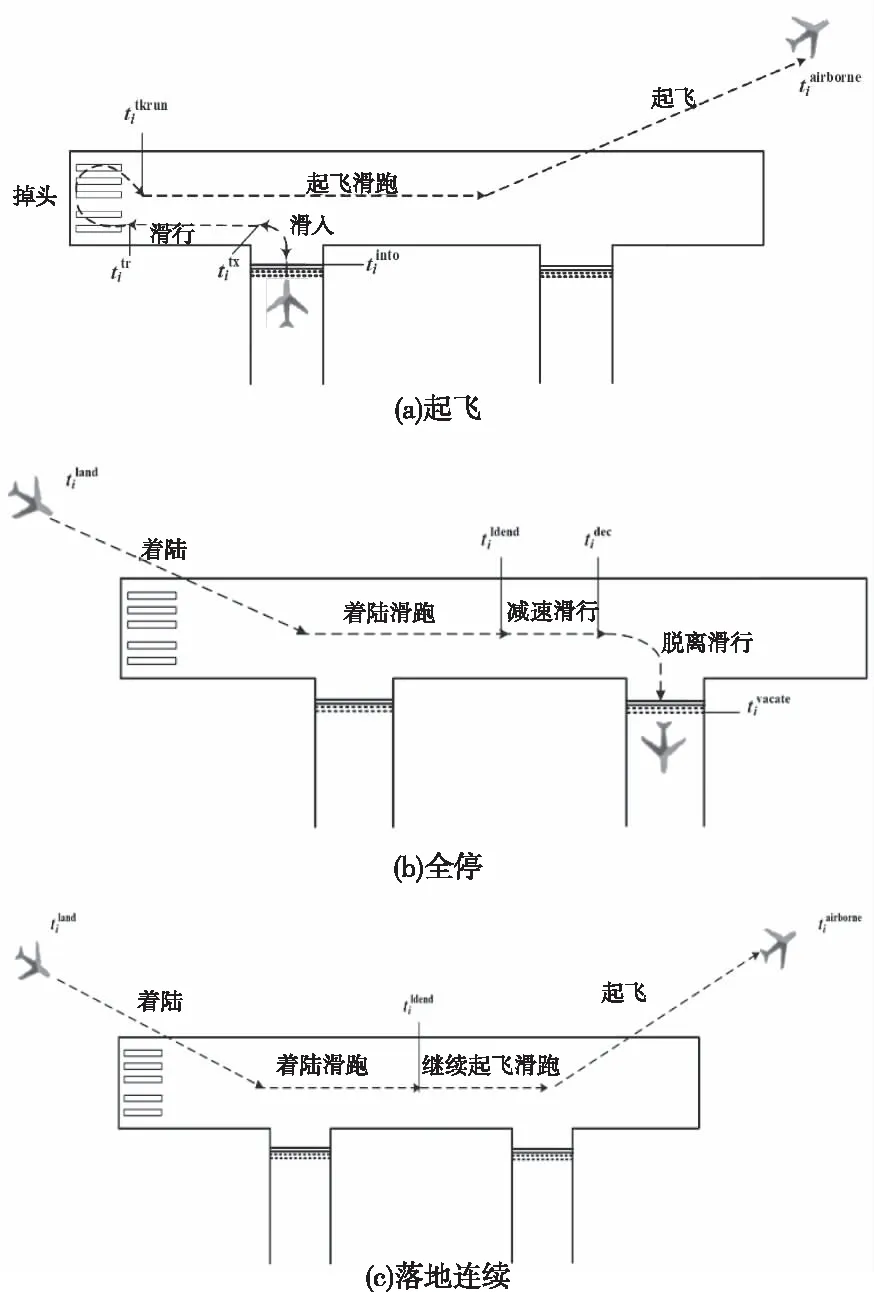
图1 训练航空器运行程序
3 通航机场跑道容量评估模型
3.1 主要参数说明
1)航空器起飞和降落性能参数

2)航空器地面滑行参数
Vtr:航空器转弯速度;Vav:航空器滑行平均速度;a:航空器减速度;R:航空器转弯半径;Lturn:航空器从Vmax减速至Vtr的距离。
3)跑道滑行道结构参数
L:跑道长度;W:跑道宽度;Ls:跑道等待位置距跑道边线的长度;LT:联络道道口距跑道入口的长度;f:跑道道面摩擦系数;
3.2 起飞航空器跑道占用时间
起飞航空器穿越跑道等待位置转弯后开始滑行时刻

(1)
跑道端掉头时刻

(2)
对准跑道开始起飞滑跑时刻

(3)
起飞滑跑距离
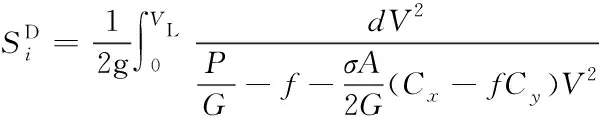
(4)
起飞滑跑和爬升时间:

(5)
起飞航空器飞跃跑道末端时刻

(6)
起飞航空器占用跑道时间

(7)

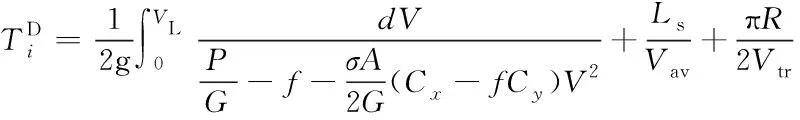
(8)
若LT>R,起飞航空器通过其它联络道做90°转弯后上跑道开始逆向滑行,至跑道起端后做180°转弯并对准跑道中线,θ=180°

(9)
3.3 降落航空器跑道占用时间
1)降落阶段
航空器降落滑跑距离:
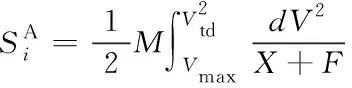
(10)
降落滑跑时间

(11)
其中
VH=(1.2~1.3)Vtd
(12)
航空器降落滑跑至最大滑行速度时刻

(13)
2)全停航空器
全停航空器着陆接地滑跑减速至转弯速度,需从最近的联络道脱离,需满足

(14)
减速距离为

(15)
减速滑行结束时刻

(16)
滑行脱离跑道时刻

(17)
全停航空器占用跑道时间为

(18)
3)落地连续航空器
落地连续航空器继续起飞滑跑距离

(19)
起飞滑跑和爬升时间

(20)
起飞时刻

(21)
落地连续航空器跑道占用时间
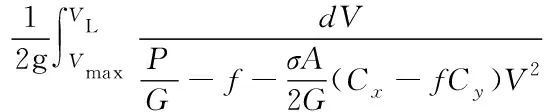
(22)
3.4 模型约束条件
根据《空中交通管理规则》,前后机fi、fj使用同一跑道起飞、降落时,应满足:
1)起飞或落地连续航空器fi已飞跃跑道末端,全停和落地连续航空器fj获得着陆和落地连续许可的时间

(23)
2)起飞或落地连续航空器fi已飞越跑道末端,起飞航空器fj获得进入跑道的许可的时间
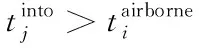
(24)
3)全停航空器fi脱离跑道后,全停和落地连续航空器fj可获得着陆和落地连续许可的时刻须满足

(25)
4)全停航空器为fi应脱离跑道后,起飞航空器fj可进入跑道的时刻须满足

(26)
3.5 跑道容量计算
单跑道容量评估模型可抽象为单位时间T与起飞、全停、落地连续航空器占用跑道时间期望的比值
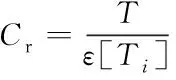
(27)
ε[Ti]为一段时间内起飞、全停、落地连续航空器占用跑道时间的平均时间,若该段时间起飞航空器架次为J,降落航空器架次为F,降落航空器中有m架全停航空器,n架落地连续航空器,则

(28)
由此,单位时间T内跑道容量为

(29)
4 仿真结果和数值分析
广汉机场为中国民用航空飞行学院主要训练机场,利用VC++和MATLAB编程,以该为例进行仿真模拟分析。如图2所示,机场跑道长度L=2200m,宽度W=45m,跑道运行方向为13号时,起飞航空器由距跑道入口为LT1=600m的1号联络道上跑道,全停航空器经由与跑道入口LT2=1100m和LT3=1500米的2号和3号联络道脱离跑道,三条联络道与跑道中线夹角为θ=90°。

图2 广汉机场跑滑结构示意图

通过分析数据可知,当α=0.5,不同方向跑道容量最大值均为80.58架次,13号跑道容量最小值为36.41架次,平均值为52.33架次,分别比31号跑道增加了5.99%和2.02%,标准差为10.33,比31号跑道降低了5.98%。当λ=0.5,不同方向跑道容量最大值均为80.06架次,13号跑道容量最小值为37.63架次,平均值为51.42架次,分别比31号跑道增加了5.81%和2.02%,标准差为7.85,比31号跑道降低了9.15%。
由此可见,不同运行方向跑道容量最大值虽然相同,但13号跑道容量最小值和平均值较大,且当α、λ和ΔS变化时,容量标准差较小,说明13号跑道服务水平较为稳定,随起降比,全停和落地连续比、航空器起落滑跑距离等动态因素变化较小。31号跑道平均容量和最小容量均小于13号跑道,且受动态因素影响较为明显。可见,在进行训练飞行时,广汉机场应尽量使用13号跑道从而获得更高和更稳定的训练效率。
由图2可知,广汉机场13号跑道配备了仪表着陆系统和Ⅰ类精密进近灯光系统,而31号跑道若进行仪表飞行训练时,只能进行非精密进近训练,说明在实际运行时,该机场也主要使用13号跑道。可见,本文模型的容量评估结果与该机场实际训练情况相符。
对比图3、图4可知,13/31号跑道容量随α、λ和ΔS的变化趋势基本一致,这是由于三条联络道基本对称且位于跑道中部,起飞航空器从不同方向进入跑道滑行至跑道端的时间基本相同,而全停航空器从不同方向脱离跑道时间也基本一致。

图3 不同方向跑道容量随ΔS,α的变化趋势(λ=0.5)
分析图3数据可知,由于落地连续航空器占用跑道时间较全停航空器短,因此跑道容量随α增大而增大。ΔS∈[0,130m],全停航空器接地位置随ΔS增大,距离2号联络道越近,脱离跑道效率提高,因此容量基本保持不变。ΔS>130m,全停航空器只能继续滑行至3号联络道脱离,使跑道占用时间增加,造成跑道容量突然减小。ΔS∈[140m,500m],由于全停航空器接地位置离逐渐接近3号联络道,脱离效率再次提升,混合容量又进入平台期。
分析图4数据可知,跑道容量随ΔS,λ变化趋势与图3相似,仍呈阶梯型增减。若λ较小,降落航空器对跑道容量影响更大。受全停航空器着陆滑跑距离和脱离效率的影响,ΔS∈[0,130m],跑道容量与ΔS呈正相关。ΔS∈(130m,140m),由于全停滑跑距离超过1100m,全停航空器经由3号联络道脱离,脱离效率较低,跑道容量大幅度减少,且减小程度与λ呈负相关。当ΔS∈[140m,500m],全停滑跑距离接近1500m,减速和脱离滑行越短,容量值再次增加。同时,随λ增大,单位时间内起飞航空架次增加,由于起飞滑跑时间与ΔS呈正比,因此λ较大时,跑道容量随ΔS逐渐减少。
由以上分析可知,起降比、全停和落地连续比、起落滑跑距离和联络道位置等因素综合影响跑道容量。在保证安全间隔的条件下,增加起飞和落地连续比例,能有效提高训练效率;飞行员可目视判断飞行高度,合理选择触地位置,使降落滑跑结束位置更接近联络道口,从而提升跑道容量;飞行员及时掌握航空器抬前轮时机,能减小起飞滑跑距离,提升起飞效率和安全性;训练飞行时,若满足逆风、干燥道面,上坡起飞和下坡着陆等条件,可有效减小起落滑跑距离,提高跑道容量。
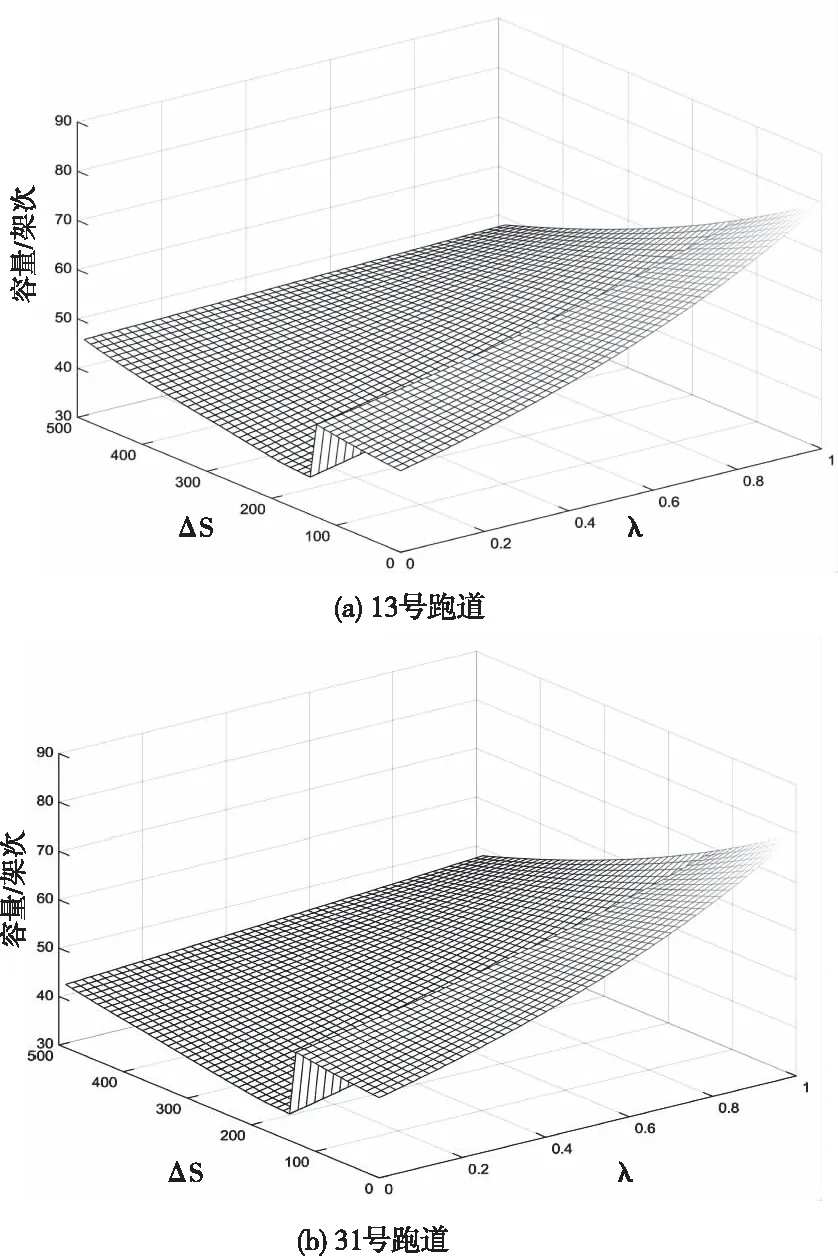
图4 不同方向跑道容量随ΔS,λ的变化趋势(α=0.5)
5 结论
本文通过分析训练飞行航空器使用跑道、滑行道的运行规则,考虑训练科目的差异,量化了航空器起飞、全停、落地连续跑道服务时间,引入管制间隔,建立通航训练飞行跑道容量评估模型,并对模型进行仿真验证。结果表明,本文模型能根据实际机场跑滑结构计算不同起降比、全停和落地连续比的跑道容量,使用该模型进行容量评估的结果与机场实际运行一致,在保证安全的条件下,能对培训机构制定训练飞行计划提供有效的参考依据。
