无资料地区洪水预报参数估计

冯晓乐，王利书，2，龙 岩，康爱卿

（1.河北工程大学水利水电学院，河北 邯郸 056038；2.河北省智慧水利重点试验室，河北 邯郸 056038；3.中国水利水电科学研究院，北京 100038）

1 引言

洪水预报的精准性与研究区域资料的完整度和监测设备的覆盖度密不可分，基于水文站建设数量的局限性，我国无资料地区的流域面积占比较大。2003年7月，国际水文科学协会首次正式提出了无资料流域水文预报计划（Predictionin Ungauged Basins，以下简称PUB），旨在通过有资料地区的参数与无资料地区水文基础资料的参证融合，从而建立适合无资料地区水文预报模拟的新模型，达到有资料地区水文预报的经验做法和数据资料在PUB计划的实施下向无资料或缺资料地区拓展[1]。PUB计划的提出，有效推动了无资料地区径流预报的发展。

随着产汇流理论的进步与计算机技术、GIS技术、遥感技术等发展，水文模型逐渐从集总式向分布式发展[2]，计算误差逐渐降低，参数的敏感性分析与智能优化方法也在持续更新迭代。使用水文模型，需要有效足够的洪水资料率定模型参数进行精准的洪水预报，而对于缺乏资料的地区，模型的限制在于参数估计与参数移植。徐长江等[3]根据已有资料及参数特征值对湘江流域洞庭湖水系中无资料地区进行参数区域化移植，模拟效果良好。杨邦等[4]以流量历时曲线为拟合对象，根据曲线的拟合过程反馈无资料地区参数，从而实现区域化参数估计。施征等[5]基于流域特征值的相关关系，根据Pearson相关系数分析变量相关关系并通过聚类分析确定与目标流域最相似的流域进行参数移植并取得良好效果。姚成等[6]基于地貌单位线相似的流域参数进行无资料地区参数移植，应用效果较好。

本文以广州市内流溪河水库、黄龙带水库等9个水库流域为研究对象，基于三水源新安江模型，以粒子群算法作参数优化进行洪水预报。假设其中的芙蓉嶂水库为无资料地区，运用已有资料流域的流域特征值，比较距离相近法、面积相似法、参数综合法、区域回归法的参数移植模拟结果与实测数据，经分析对于芙蓉嶂水库来说多元回归法参数移植效果较好。

2 研究区概况与研究方法

广州市位于低纬度区，北回归线横穿市区北部，太阳辐射量大，日照时间长，属南亚热带季风气候区。据统计，全年平均气温为21.4～21.8℃，最冷月1月平均气温为13.3℃，最热月7月平均气温为28.4℃，极端最高气温为38.7℃，极端最低气温为0.0℃左右。全年无霜期超过340 d，平均相对湿度79%，属于湿润地区。

根据广州市雨量站1908—1998年资料统计，广州市多年平均年降水量为1675.5 mm，实测最大年降水量为2865 mm（1920年）、最小年降水量为1061 mm（1991年）。根据年降水量差积曲线分析发现，年降水量的丰枯循环期一般20～30 a，这说明广州市降水量的年际变化相对比较稳定。多年平均年水面蒸发量约为1000～1400 mm。

本次研究流域为流溪河流域，经子流域划分后取流溪河水库、黄龙带水库、九湾潭水库、芙蓉嶂水库、福源水库、三坑水库、茂墩水库、和龙水库、天湖水库9个子流域为研究对象。根据已知出库流量与各水库库容曲线进行入库反推，各水库均具有较丰富的水文资料。图1为研究区流域概化图。

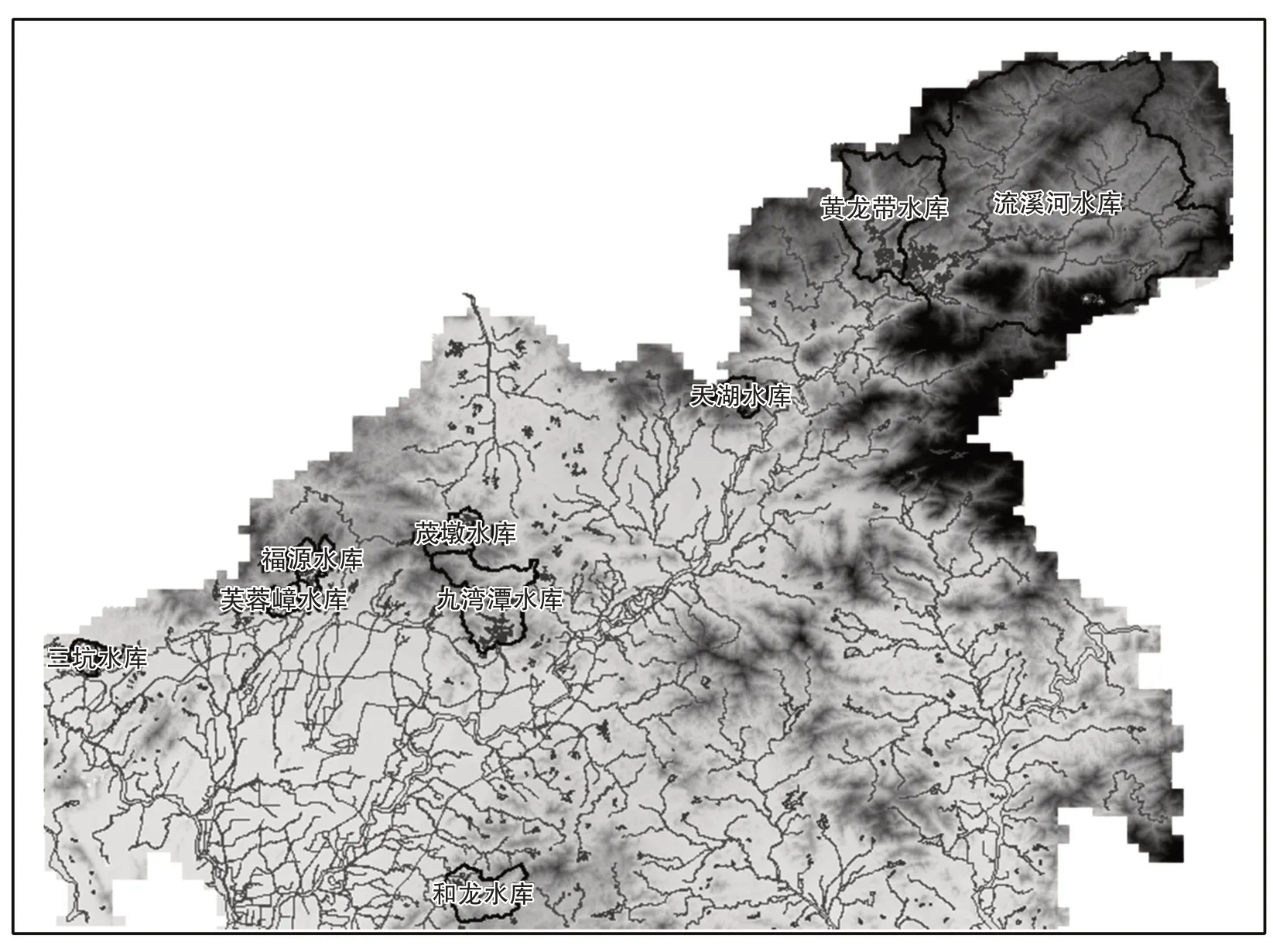
图1 研究区流域概化图

3 模型搭建

3.1 新安江模型介绍

新安江模型[7]是河海大学赵人俊教授在1963年提出的，模型基于蓄满产流原理。新安江模型是一个完整的概念性模型，在我国湿润、半湿润地区得到了广泛的应用。其中，三水源新安江模型[8]应用较为广泛，其主要特点划分单元、分水源、分阶段，计算流程如图2所示。分单元是把流域划分成若干个子流域，有效降低时空降雨分布不均匀及下垫面不同所带来的影响；分水源是指将径流分成地表径流、壤中流、地下径流；分阶段是指将汇流过程分为流域汇流阶段和河网汇流阶段，流域汇流计算采用线性水库法，河道汇流采用马斯京根分段连续演算或滞后演算法。新安江模型参数共17个，其中敏感参数共12个，详见表1。

表1 模型参数含义及其敏感程度

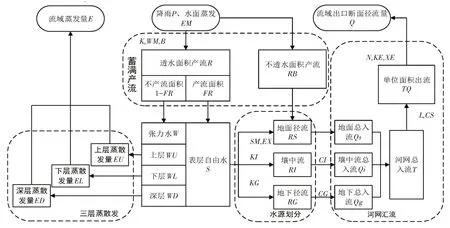
图2 新安江模型计算流程

3.2 粒子群参数优化算法

水文模型的参数分为人工率定法和智能优化算法两类。在参数率定过程中，人工率定法往往依赖于模型工作者丰富的工作经验，率定后的参数集模拟效果较好，但往往并非是参数的全局最优解。智能优化算法是在模型的率定期根据模拟值的误差与参数组建立数学关系寻找全局最优解，目前主要采用的优化算法包括罗森布瑞克法、单纯形法和遗传算法。

本文中参数优化采用粒子群优化算法。粒子群优化算法（Particle Swarm Optimization，以下简称PSO）是1995年由Eberhart和Kennedy提出的一种新兴的集群智能优化算法[9]，它起源于对鸟群和鱼群觅食行为的研究。PSO优化算法和遗传算法（Genetic Algorithm，以下简称GA）在进化技术方面有很多相似之处，2种算法都是多点搜索。应用PSO优化计算时，目标函数的解相当于搜索空间的一只鸟的位置，一般称这些鸟为粒子或者主体，每个粒子都有各自的位置和速度，用于决定优化的方向和距离，还有一个由目标函数决定的适应值，用来衡量粒子的优劣。每个粒子通过更新各自的位置和速度在解空间中搜索当前的最优解，并以此为依据寻找下一个解，直至达到设定的最大迭代次数和适应阈值停止搜索，最后得到全局最优解。近些年来，粒子群优化算法在水文模型参数优选方面得到了广泛应用，效果显著。为消除模型参数初始值设定对模型优化结果的影响，本文选取率定期资料的第一年资料作为水文模型的预热期。

3.3 误差评定

本文中洪水预报精度评定根据《水文情报预报规范》（GB/T 22482-2008）选择洪峰、径流深和峰现时间，洪水预报误差指标采用确定性系数。其计算公式为：

式中：DC为确定性系数（取2位小数）；y0(i)为实测值；y c(i)为预报值；-y0为实测值的均值；n为资料序列长度。

3.4 模拟结果

建立基于粒子群算法的三水源新安江模型，对研究区内9个水库子流域进行模型演算，其结果详见表2。另外，以流溪河水库为例画出了2021年日流量模拟过程，如图3所示。由表2可知，新安江模型普遍适用于流溪河流域内洪水预报。其中，流溪河、黄龙带、芙蓉嶂、福源、三坑、茂墩、和龙水库确定性系数与合格率均在0.7以上，说明模拟效果较好，精度为乙级。九湾潭水库与天湖水库确定性系数与合格率在0.6以上，说明模拟效果一般，精度为丙级。

表2 各子流域新安江模型模拟结果

4 流域特征值与参数移植

4.1 流域特征值分析

流域特征值是指一个流域的坡度、植被、流域面积、地形地貌、流域形状等反映其物理性质的系数，这些系数取决于每个流域独特的地理条件，也影响水文循环的速率。本文取流域平均坡度、多年平均降水量、流域面积、流域形状系数、植被覆盖率这5种流域特征值。

流域平均坡度影响着地表径流的产汇流速率，本文基于DEM栅格数据，在ArcGIS中根据等高线的间距面积及长度计算得来。多年平均降水量是衡量流域气候特征的重要指标，流域面积反映了流域分水线包含的范围，流域面积越大流域内水库库容越大。流域形状系数是流域分水线的实际长度与流域同面积圆的周长的比，越接近1流域面积更接近圆，易产生大洪水，越接近0流域形状越狭长，径流变化越平缓。植被覆盖率是指森林面积在流域内的占比，反映了流域的下垫面条件及模型的下渗蒸发速率。各水库流域特征值，详见表3。

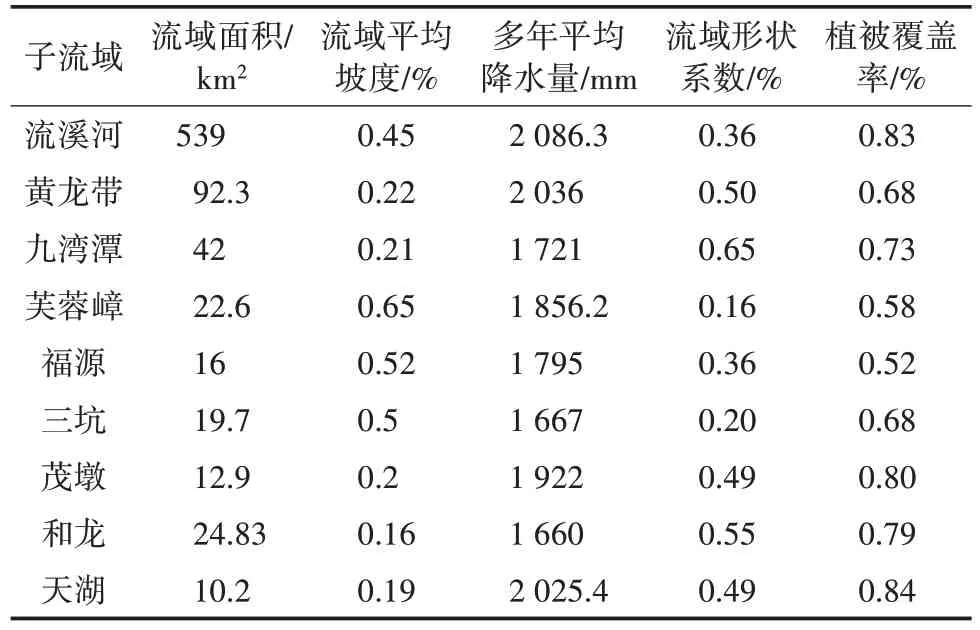
表3 各水库流域特征值

4.2 基于流域特征值的参数移植方案

针对流溪河流域的山洪特性，识别水文要素空间变异性，分析水文要素与典型流域地形地貌等地理要素之间的相应关系，提出具有一定尺度协调性的小流域产流计算方法，寻求产流参数区域规律，实现无资料地区的参数移植。

目前对无资料地区径流预报常用的方法为区域化方法。该方法是在一定范围内，将有资料流域的水文信息比如水文模型参数通过一定的方法移植到无资料流域，从而实现对无资料流域的预报。由于区域化方法能够利用流域下垫面特征值等信息，所以能够有效地降低不确定性影响，从而提高预报精度。常用的区域化方法有多元回归法、空间邻近法、流域物理特性相似法以及全局平均法。

4.2.1 距离相近法

根据参证流域与本流域形心的距离，取距离最近的流域参数进行移植。基于ArcGIS软件中的计算几何功能，可确定流域质心的x，y坐标，各子流域质心坐标统计根据各子流域间的距离确定，按距离大小进行排序，离无资料流域最近的子流域区间即为福源水库，引用其参数用于模型计算。

4.2.2 面积相似法

根据参证流域和本流域面积的差值，取流域面积最相似的参证流域的参数进行参数移植。基于ArcGIS软件中的计算几何功能[10]，计算子流域面积，按面积差值大小进行排序，面积差值最接近的流域为和龙水库，引用其参数用于模型计算。

4.2.3 参数平均法

统计全流域内已有资料的流域，统计各子流域参数的平均值，对无资料流域进行参数移植。

4.2.4 多元回归法

多元回归分析基于流域特征值和已率定敏感参数的相关关系[11]，分析各特征值对敏感性参数的影响因子，建立参数的多元回归方程，根据无资料流域的特征值进行逐个插值。

基于SPSS软件，以新安江模型参数为因变量、以流域下垫面物理特征值为自变量建立多元回归方程，根据多元回归方程和无资料地区的下垫面特征值反推出模型参数值，进而完成参数估计。

4.3 参数移植模拟结果

本文假定芙蓉嶂水库为无资料地区，运用已有资料基于流域特征值进行参数移植，采用距离相近法、面积相似法、参数平均法与多元回归法分别模拟芙蓉嶂水库2020年5月1日—2020年7月15日洪水预报，具体参数详见表4，各方法模拟流量过程线依次如图4—7所示。

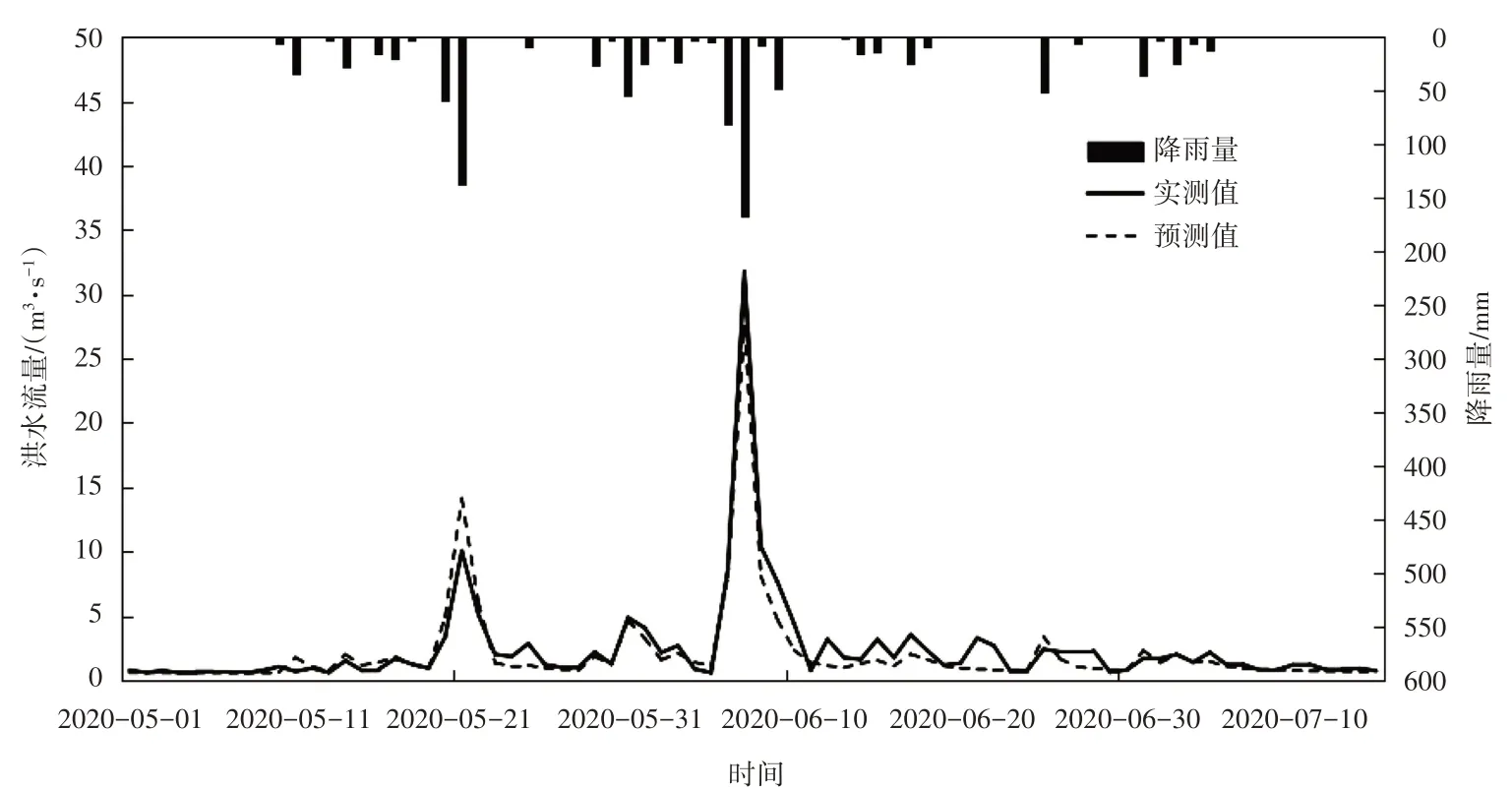
图4 距离相近法参数移植后模拟结果

从表4可知，在本次参数移植中，4种参数移植方案模拟结果均达到乙级预报精度。其中，多元回归法确定性系数最高，模拟入库流量峰值与实测值误差最小，模拟效果较好，其次为距离相近法、面积相似法，最差为参数平均法。

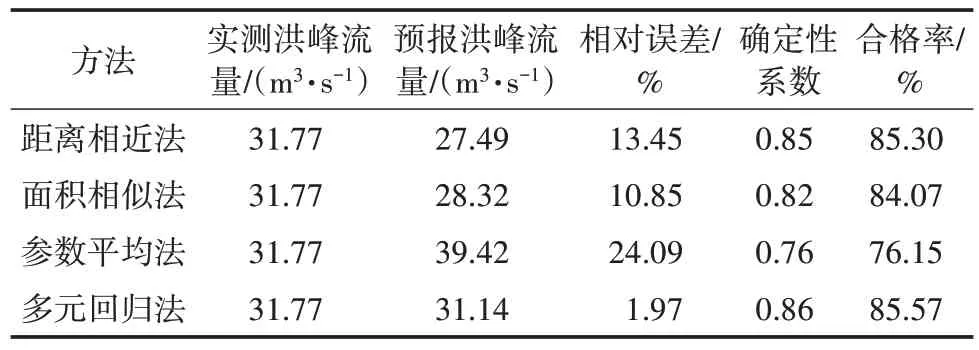
表4 参数移植后芙蓉嶂水库模拟结果

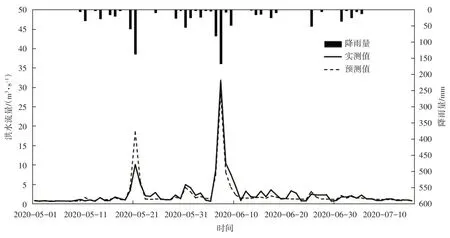
图5 面积相似法参数移植后模拟结果

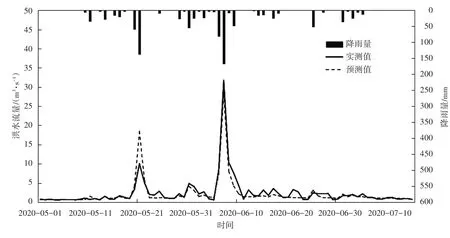
图6 参数平均法参数移植后模拟结果

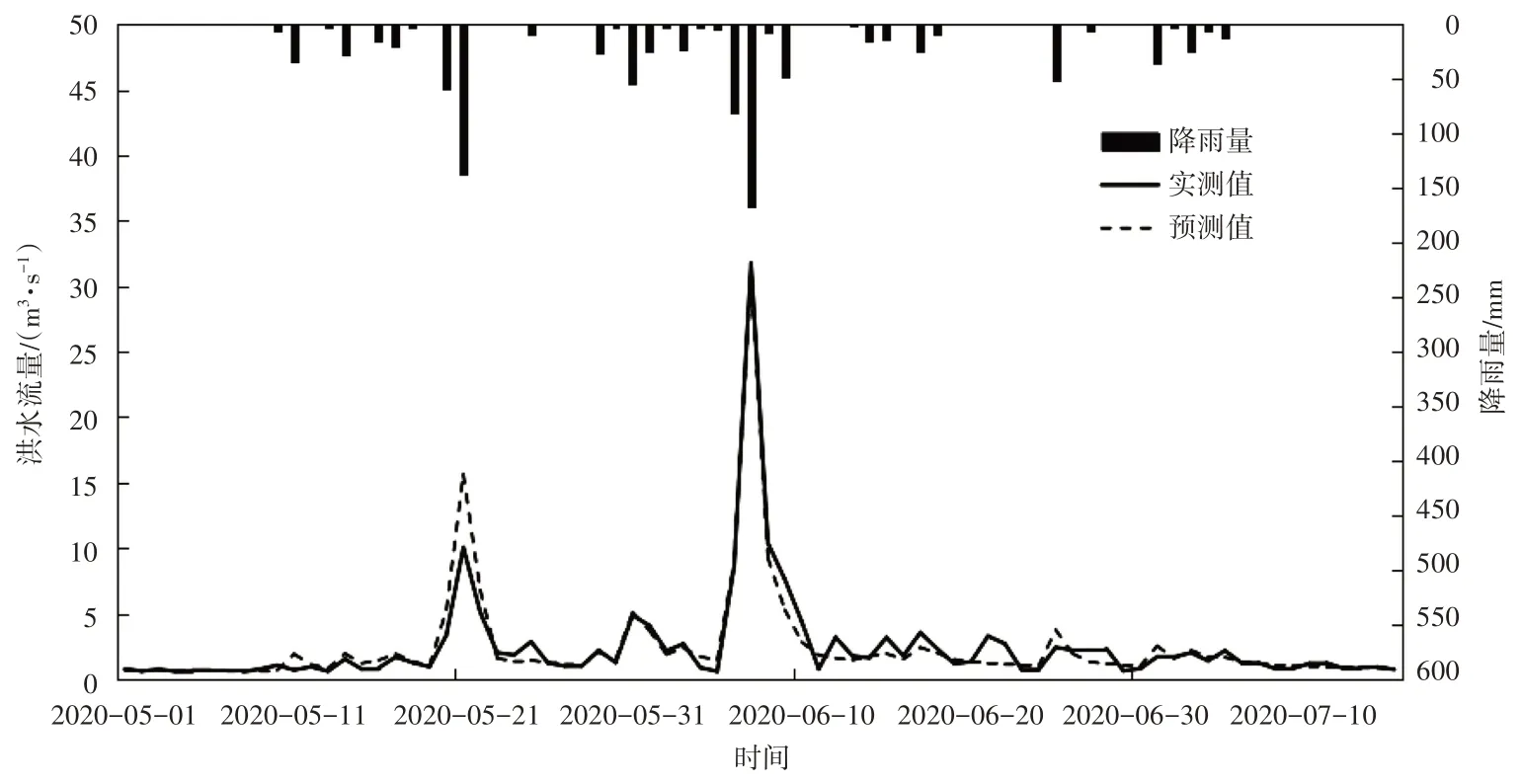
图7 多元回归法参数移植后模拟结果

5 结论

（1）本文采用三水源新安江模型，对广州市内9个水库进行洪水预报，模拟结果显示7个水库预报达到乙级精度标准、2个水库预报达到丙级标准，证明新安江模型对于流溪河水库、黄龙带水库等洪水预报是适用的。

（2）本文提出基于流域特征值和敏感性参数的多元回归法，分析流域特征值与敏感参数的相关关系，为无资料地区参数移植提供了思路。假定芙蓉嶂水库为无资料地区，通过分析流域特征值，选用距离相近法、面积相近法、参数平均法、多元回归法进行参数移植，其中多元回归法参数移植效果最好。

（3）本文在参数移植过程中仍有需改进之处，如水文模型参数存在异参同效现象[12]。芙蓉嶂水库在初始率定参数时确定性系数达0.87，合格率达86.44%；而在参数移植后确定性系数达0.86，合格率达86.57%，误差相似情况下而敏感性参数间仍有较大差距，说明模型的异参同效现象是存在的，也是参数移植问题的关键所在。