基于高斯过程的参数辨识及永磁同步电机模型电流预测控制策略

魏宗恩， 邓永停， 乔延婷， 费 强， 李洪文

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100039； 3.陆军装甲兵学院士官学校，吉林 长春 130000；4.季华实验室， 广东 佛山 528200）

1 引言

永磁同步电机（Permanent Magnet Synchronous Motor， PMSM）因其可靠性高、体积小、控制精度高等优点在光电跟踪设备［1-2］、高精度数控机床、航空航天领域得到广泛应用，同时，永磁同步电机也被广泛应用于新能源汽车领域。因此，对高性能的永磁同步电机控制算法［3-4］的研究具有重要意义。基于有限控制集的模型预测控制［5］（Finite Control Set Model Predictive Control， FCS-MPC）算法利用代价函数，通过预测不同电压对应的电流来选择逆变器的开关状态。该策略的优点是瞬态响应快、实现简单、无需调制。然而，直接使用系统模型来选择最优控制行为，使得系统在建模错误或参数变化的情况下，出现性能变化［6-8］。因此，预测模型误差的影响［9-10］是FCS-MPC的重要问题。针对上述问题，传统的方法是建立更为精确的物理模型，或者设计复杂高阶求解器。这增加了系统的复杂度，造成过高的计算负荷。也有许多其他方案被国内外学者提出，其中，无模型预测控制方案［11-12］和基于参数辨识的预测模型优化控制方案成果显著。

基于参数辨识的预测模型优化控制方案在保证控制性能的前提下进一步提高系统鲁棒性。目前，永磁同步电机参数辨识方法分为离线估计方法［13-14］和在线估计方法［15-17］。此外，模拟解析方法，特别是有限元分析［18］，也被归类为离线参数估计技术，此技术常被用来作为其他辨识方法实验的实际参考。在线估计方法中，基于机器学习的方法备受关注，其通过数据来进行预测，随着有效数据的积累，机器学习的预测能力可以持续的进化，预测精度不断提高，目前，神经网络（Neural Network， NN）［19］、遗传算法（Genetic Algorithm， GA）［20］和粒子群优化（Particle Swarm Optimization， PSO）［21-22］等算法已应用于电机控制的自调试［23-24］和状态监测。

一般机器学习的算法在系统参数辨识的应用过程中需要进行超参数的调试，如神经网络中的学习率、隐藏层的数量，支持向量机中的正则化常量等。目前，应用于参数辨识机器学习的算法中，大都需要基于经验与不断测试对超参数进行优化，以提高学习的性能和效果，此过程增加了辨识算法的实施难度。另外，机器学习回归算法预测精度的评估需要衡量预测值与实际参数值之间的误差，此“实际的参数值”是基于其他辨识方法得到的，在参数辨识过程中，缺乏实时性的性能指标对预测结果进行评估。

高斯过程作为一种“非参数”机器学习技术，其超参数使用极大自然法或蒙特卡洛方法自适应获取，这简化了超参数调试的过程，并增加超参数选取的可解释性。此外，高斯过程是一个具有概率意义的学习机，可对预测输出做出概率解释，其赋予预测结果的置信度指标可用于预测效果的评估。基于上述两点，本文提出基于高斯过程的永磁同步电机参数辨识方法并与有限集电流预测控制相结合，对PMSM进行精确控制。

2 永磁同步电机电流预测模型

在理想状态下，PMSM在d-q轴坐标下的电压方程为：

PMSM磁链方程为：

其中：ψd为d轴总磁链，ψq为q轴总磁链；vd和id分别为d轴电压和电流，vq和iq分别为q轴电压和电流，Rs为定子电阻，Ld和Lq分别为d轴和q轴电感，ψm为定子磁链，ωr为电机的角速度。

通过式（1）和式（2）可得PMSM连续空间状态方程：

上述连续状态空间方程采用欧拉法进行离散化化处理：

其中：Ts为采样周期，i(k)为k时刻（k=1，2，3，…）电流值，i(k+1)为下一采样时刻电流值。因此，PMSM电流预测模型可由式（3）和式（4）得出：

其中：id(k)，iq(k)分别为k时刻的d轴和q轴电流，id(k+1)，iq(k+1)分别为k+1时刻的d轴和q轴电流。

3 PMSM电流预测模型失配影响

将PMSM电流预测模型表达式简化为：

其中：Di=(1-RsTs/Ls)，Dv=Ts/Ls，表贴式永磁同步电机d轴和q轴电感相等，用Ls表示。空间矢量角度分析，式中预测电流矢量i(k+1)由实际电流矢量i(k)与实际电压矢量v(k)加权合成。

以d-q轴电感参数为例分析模型失配对系统控制性能的影响。当系统模型未失配时，预测电流可表示为：

其中：ir(k+1)为无失配预测电流，Lrs为电感真实值。当系统模型失配时，预测电流可表示为：

其中：ip(k+1)为失配预测电流，Lp s为电感标定值。由式（7）和式（8）可得：

对式（9）进行z变换：

由此得到此离散系统极点为：z=-Lrs/Lps+1，令，m=1时，系统零极点如图1（a）所示，系统极点位于原点，冲激响应如图1（b）所示，电流实现无差拍跟踪。系统模型参数正向失配，并考虑实际情况，在0.5＜m＜1的情况下，系统z域零极点分布图如图1（c）所示，系统极点位于正实轴且在单位圆内，冲激响应如图1（d）所示，响应呈指数衰减，m数值与电流响应速度成正相关。

图1 系统性能分析图Fig.1 System Performance Analysis

系统模型参数负向失配即在1＜m＜1.5的情况下，系统z域零极点分布图如图1（e）所示，系统极点位于负实轴，冲激响应如图1（f）所示，电流阶跃响应呈指数衰减，m数值与电流响应速度成负相关。

由上述分析可知，系统模型不同失配程度会对系统性能造成不同影响，对于模型预测电流控制，此影响体现在电流控制效果上，图2展示了在传统FCS-MPC策略下，电感Ls不同失配程度下q轴电流表现。如图所示，在电感参数正向失配的情况下，q轴电流参考值相较于实际q轴电流会产生上偏移现象，而且偏移的程度与电感参数失配程度成正相关。在电感参数负向失配的情况下，q轴电流参考值相较于实际q轴电流会产生下偏移现象，而且偏移的程度与电感参数失配程度成正相关。通过图2（a）与图2（e）、图2（b）与图2（f）、图2（c）与图2（g）三组对比分析，在失配幅度相同的条件下，电感参数负向失配时会造成更严重的偏移现象。这表明电感变化对FCSMPC性能的影响是不对称的，在预测模型高估实际电感值的情况下更具危害性。

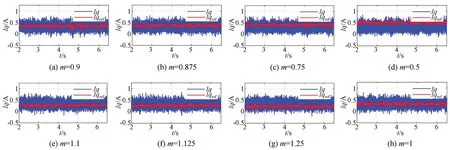
图2 电感不同失配程度下的q轴电流响应Fig.2 Performance of q-axis current with different degrees of inductance mismatch

经上述分析可知，电感参数的失配程度与电流实际表现存在某种关系。将电流表现数据作为输入，电感参数的失配程度数据作为输出，通过高斯过程回归模型的训练，可建立起输入变量到输出变量的映射关系。通过此关系，在电流状态已知的情况下可推得模型失配程度，进而求得实际参数值，实现系统模型的在线优化。

4 基于高斯过程的参数优化方案

4.1 训练数据的获取与预处理

高斯过程作为机器学习的方法，需要量化数据作为支撑。上文描述q轴电流参考值相较于实际q轴电流偏移程度，可量化为电流偏移度P。电流偏移度P描述q轴电流iq对q轴参考电流iqref上偏移程度P_u和下偏移程度P_d的比例关系：

其中：n为单检测周期内数据量，λ为偏移度系数，用作数据标准化处理，初始值设为1。

电感值不同失配程度下的q轴电流偏移度如图3所示，电流表现通过量化数据分析，电感参数的正、负向失配对电流的影响是不对称的，不同失配程度下电流偏移度P的数据作为高斯过程回归模型的训练输入之一。

图3 电感不同失配程度下的q轴电流偏移度PFig.3 Current offset of q-axis under different mismatch

q轴电流表现另一重要量化数据为电流波动度B，其描述q轴电流iq以q轴参考电流iqref为基准的波动程度：

然而这一指标随电感参数失配程度的变化呈现复杂的变化趋势，以此指标作为高斯过程回归模型的另一训练输入，其变化规律通过高斯过程算法学习。图4为实时获取部分训练数据集的三维散点图，随着电流偏移度和电流波动度的变化，电感标称值呈螺旋上升的变化趋势。

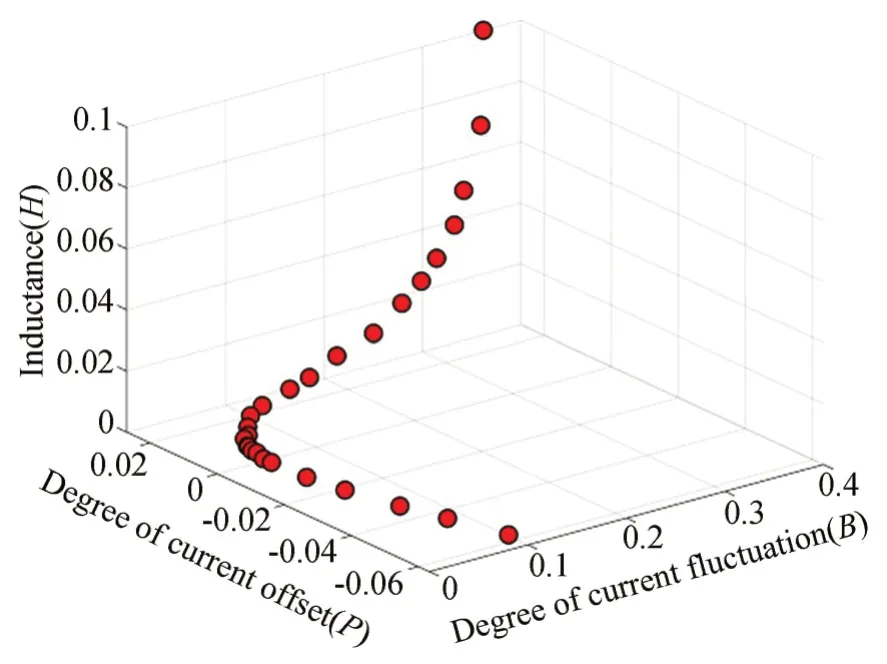
图4 训练数据集的三维散点图Fig.4 Scatter plot of training dataset

4.2 高斯过程回归模型

区别于传统参数优化方法，高斯过程参数优化作为一种机器学习的方法依赖于有效数据的训练。

假设训练数据集有n个样本，则此数据集可表示为{y，α，β，γ}，其中，电流波动度B和电流偏移度P分别用α，β来表示，γ是参数标称值，以上三项作为训练输入数据，y是参数实际值，作为训练输出数据。

测试数据集用{y*，α*，β*，γ*}表示，为表述方便，令多维训练输入数据集{α，β，γ}=x，令多维测试输入数据集{α*，β*，γ*}=x*，测试输出数据表示为y*。

与高斯分布描述数据的分布规律类似，高斯过程（GP）描述的是函数的分布。均值函数m(x)和协方差函数k(x，x′)决定了高斯过程全部的统计特征，因此，定义高斯过程为：

对于实际问题，还需考虑噪声ε对观测值的影响，因此，模型描述为：

其中：进一步假设噪声ε符合均值为0，方差为σ2的高斯分布：ε～N(0，σ2n)，且其独立于f(x)。此时，实际函数值y服从高斯过程：

其中：

训练样本与一个测试点的联合分布为：

其中：K表示协方差矩阵K(x，x)，描述训练数据x内部相关性；KT*表示协方差矩阵K(x，x*)，描述训练数据x与测试点x*协差关系；K*表示协方差矩阵K(x*，x)；K**表示协方差矩阵K(x*，x*)，描述测试点x*内部相关性。上述协方差矩阵K中元素kij是由协方差函数确定的，即kij=k(xi，xj)。

根据贝叶斯公式及式（16）得：

其 中 ，[μ2+K*K-1(y-μ1)] 和 [K**-K*K-1KT*]分别为预测均值y*和预测方差var(y*)。预测均值即为目标参数预测值，预测方差即为得到此预测值的概率评估。

在本文训练数据统计特征下，高斯过程回归模型均值函数选择为零均值函数，核函数选择为Matérn协方差函数：

其中：d=(x-x′)T(x-x′)，{σf，ρ}为超参数θ。

本文用最大似然估计法确定高斯过程核函数中的超参数θ，似然函数为：

取f为高斯过程模型f～GP(0，Σ)，则负对数边际似然为：

超参数θ的最优解通过L偏导获得：

在上述设计的高斯过程算法基础下用训练数据进行在线训练，节省了一般机器学习算法的超参数调试过程，随预测值同时输出的预测方差经预处理后作为预测效果的评估，可实时监测预测状态以及异常数据。

高斯过程回归预测模型精度主要受其核函数影响，为了验证本文中核函数相较于其他常用核函数在此数据类型和规模下具有更高的预测精度，随机选择10组测试数据分别在以平方指数协方差函数、有理二次协方差函数以及本文应用的Matérn协方差函数为核函数的高斯过程模型下进行测试。

平方指数协方差函数表达式为：

有理二次协方差函数表达式为：

系统模型参数真实值与预测值对比图如图5（a）～5（c）所示，实验结果显示，以平方指数协方差函数、有理二次协方差函数为核心的高斯过程回归算法均有较高的预测精度，但是在系统参数失配程度较高的情况下，会产生较大的预测误差，本文采用的Matérn核函数，在各种失配状态下均表现高的预测精度。

图5 系统模型参数真实值与预测值对比图Fig.5 Comparison of actual and predicted values of system model parameters

4.3 基于高斯过程参数辨识的模型预测控制

基于高斯过程的永磁同步电机模型预测控制系统框图如图6所示。系统通过PI控制器进行速度控制，并产生电流参考值。预测电流控制器将对该电流进行跟踪，选择能使代价函数最小化的电压矢量，将其应用于整个采样间隔。在系统运行的过程中进行电流检测，电流检测数据经预处理模块得到电流波动度B和电流偏移度P，此两项作为高斯过程回归参数优化模块的输入进行系统参数的预测，预测结果将更新预测电流控制器中已失配的参数，使系统恢复未失配状态。

图6 基于高斯过程的永磁同步电机模型预测控制系统框图Fig.6 Block diagram of MPC system for PMSM based on GP

系统中高斯过程回归模型是不断更新的，随着训练数据的累积而进化。在不同速度参考值或不同负载条件下，稳定后的q轴电流表现量化值会有所不同，因此在不同实验条件下的实验数据将会训练新的高斯过程回归模型。

高斯过程的训练数据直接由目标算法FCSMPC获取，因此参数辨识过程对FCS-MPC不会造成类似于其他入侵式辨识算法带来的不利影响，同时，训练得到的回归模型将用来优化FCSMPC算法，实现了控制与优化的闭环。

5 实验分析

实验验证FCS-GPMPC控制策略的有效性，搭建了如图7所示的实验平台，DSP-TMS320F2 8335和FPGA-EP3C40F324组成伺服控制器。PMSM参数如表1所示。

图7 实验平台实物图Fig.7 Photograph of experimental platform

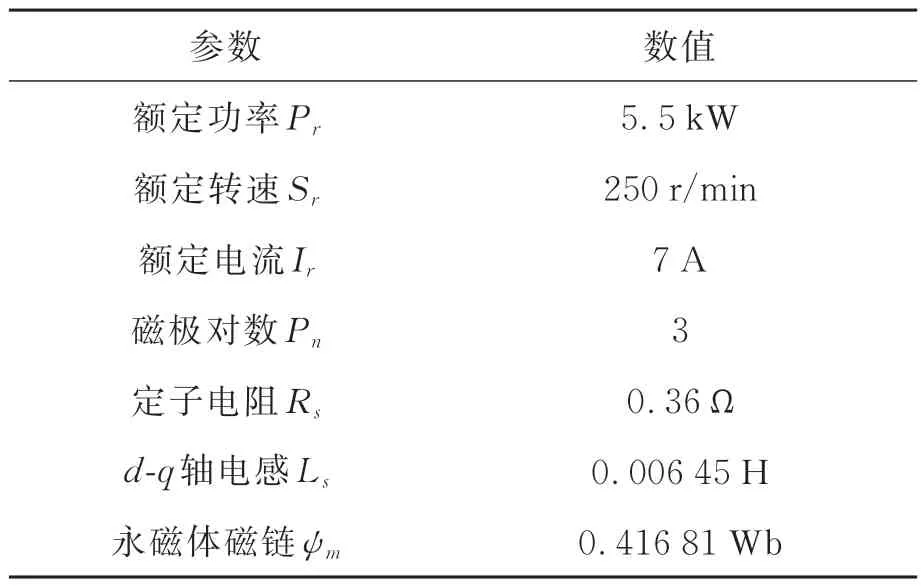
表1 永磁同步电机参数Tab.1 Parameters of PMSM

首先进行高斯过程回归模型的获取，在给定速度50 r/min、零负载条件下，电感参数标称值在以实际参数值为基准-25%～25%的范围波动，利用电流波动度等实时数据进行高斯过程回归模型的训练，得到图8（a）所示拟合曲面，通过电流波动度和电流偏移度即获得电感参数的失配信息。

为验证回归模型在不同速度条件下的自适应性能，在给定速度100 r/min、零负载条件下进行回归模型自适应获取，得到图8（b）所示的拟合曲面。为验证高斯过程回归模型在不同负载条件下的自适应性能，在给定速度100 r/min，2 N·m负载条件下进行回归模型自适应获取，得到图8（c）所示的拟合曲面。实验证明，电机运行条件不同，电流表现和参数失配之间的回归模型会有不同，本文高斯过程方法会在电机不同运行状态下自适应更新回归模型。

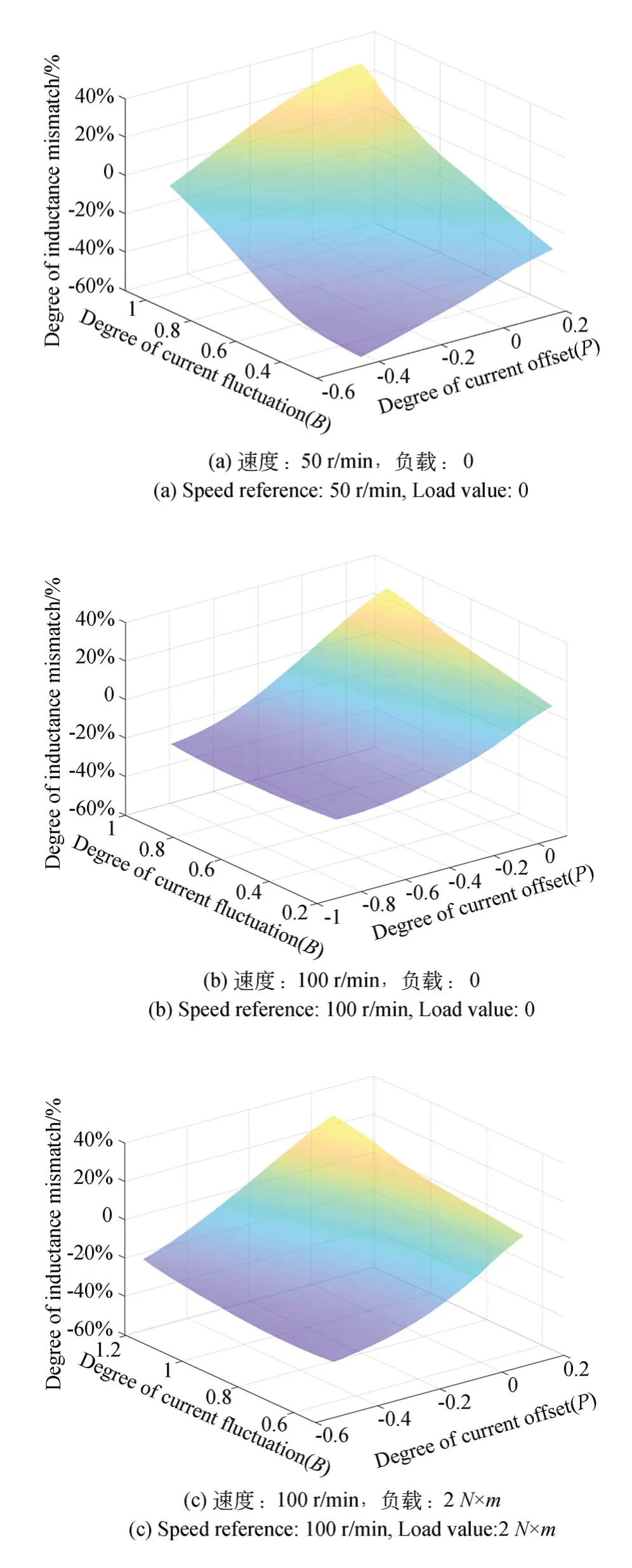
图8 不同运行条件下拟合曲面Fig.8 Fitted surfaces under different operating states

基于本文方法进行参数辨识的实验，如图9所示（彩图见期刊电子版），圆点表示该时刻实际参数值，红色曲线表示预测参数值，图中显示，预测参数曲线准确跟踪实际参数值。测试数据集显示，在本文数据类型和规模下，预测误差均控制在2%以内，均方根误差RMSE为0.002 1，已到达千分位级，R2达到0.99，接近于1。

图9 参数辨识结果Fig.9 Result of parameter identification

高斯过程回归模型在输出预测均值y*的同时会输出预测方差var(y*)，因此置信度为95%的置信区间为：。图9中灰色阴影部分即为预测值的置信区间，可用于预测效果的评估以及异常数据的检测，预测误差与置信区间的波动成正相关。为验证置信区间对异常预测值的检测能力，在系统运行的过程中加入异常值，如图10所示阴影部分即置信区间迅速扩大，这代表此时刻预测方差出现较大波动，即检测到本组数据中出现异常值或者出现较大预测误差。因此，置信区间的大小可用于预测效果的评估。

图10 预测异常检测Fig.10 Predictive anomaly detection

为进一步验证本文控制策略的稳态性能，在2 N·m负载、100 r/min速度参考值条件下，对比本文控制策略与传统FCS-MPC在参数失配情况下相电流和q轴电流状态。图11（a）、图11（b）为传统FCS-MPC策略下a相电流波形及其快速傅里叶分析（Fast Fourier Transform， FFT），图11（c）、图11（d）为本文控制策略下参数优化后a相电流波形及其快速傅里叶分析。相较于传统FCS-MPC，本文控制策略下的相电流总谐波失真（Total Harmonic Distortion， THD）由4.38%降为3.74%。

图11 相电流响应对比Fig.11 Comparison of phase current response

考虑电感参数失配程度的极限情况，参数标称值在以实际参数值为基准-50%～50%的范围随机波动。传统FCS-MPC算法q轴电流响应和基于所提方法参数优化后的q轴电流响应分别如图12（a）、图12（b）所示。相较于传统FCSMPC，所提方法q轴电流波动度降低30.5%，电流平均偏移度降低19.6%。

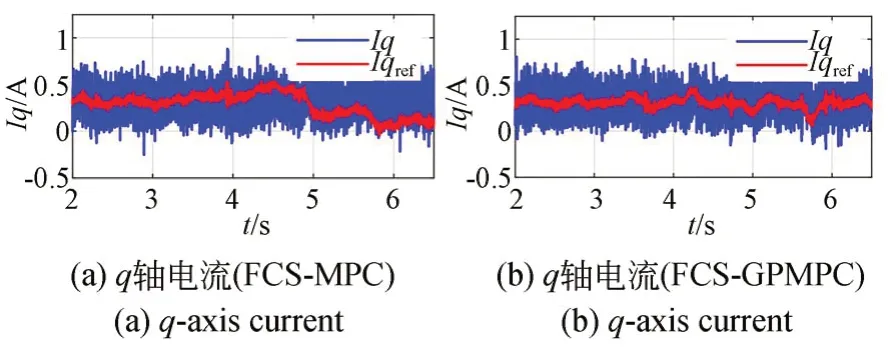
图12 q轴电流响应对比Fig.12 Comparison of q-axis current response

实验验证FCS-GPMPC控制算法对电流阶跃变化的动态跟踪性能，如图13～14所示，q轴参考电流在5 s时由0 A上升到1 A，传统的FCS-MPC算法的响应时间与FCS-GPMPC算法一致，但由于电感参数的不匹配，导致对未来电流的预测不准确，降低了电流跟踪性能。FCS-GPMPC算法及时调整电感参数标称值，因此其对参考电流的阶跃变化有更好的动态响应。

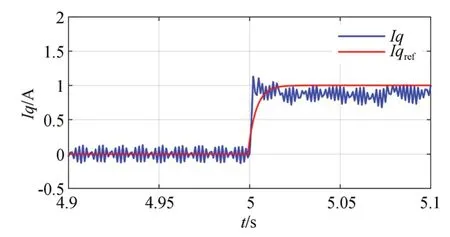
图13 q轴电流阶跃响应（FCS-MPC）Fig.13 Step response of q-axis current

6 结论

本文设计了基于高斯过程参数优化的模型预测控制器，高斯过程参数辩识方法简化了其他机器学习算法超参数的调试过程，其波动参数的精确估计提高了模型预测控制器的控制性能。高斯过程回归算法还实时提供了预测结果的置信区间，通过此置信区间，可在线进行系统算法的监测及优化。基于高斯过程参数优化的模型预测控制可实时优化预测模型，对比于传统的FCS-MPC，所提方法对电流的稳态性能和动态性能均有提升。实验结果表明：基于高斯过程回归的参数辩识方法具有较高的精度，在电感参数失配程度不断变化的情况下，实现参数的精确跟踪，预测误差控制在2%，相较于传统FCS-MPC，本文控制策略下的相电流总谐波失真也有所降低，电感失配程度随机变化下q轴电流波动度降低30.5%，电流平均偏移度降低19.6%，另外，在参数失配情况下，所提算法对q轴参考电流的阶跃变化有更好的动态响应。

图14 q轴电流阶跃响应（FCS-GPMPC）Fig.14 Step response of q-axis current