换向激励式压电振动俘能器

阚君武， 王 凯， 孟凡许*， 费 翔， 张忠华，翟仕杰，祝孟松

（1.浙江师范大学 工学院 精密机械研究所，浙江 金华 321004；2.浙江省城市轨道交通智能运维技术与装备重点实验室，浙江 金华 321004）

1 引 言

为满足便携式/可穿戴电子设备和无线传感器节点的自供电需求，基于压电、电磁及摩擦电原理的俘能器成为研究热点[1-2］。每一类俘能器都有其自身的特点及适用领域，压电俘能器的优势在于能量密度大、结构简单及无电磁干扰等，可用于收集环境中的各种能量，如人体运动能、旋转动能、风能、波浪能及振动能[3-8］。其中，振动能无处不在，且能量密度高、不易受天气等因素的影响，故国内外学者对压电振动俘能器进行了大量研究。

一部分学者通过引入非线性磁力系统来提高俘能器的输出性能，Fan[9］等提出了一种基于磁吸力的单稳态低频压电振动俘能器，通过磁力来降低俘能器的响应刚度，在随机激励下，其平均输出电压是线性压电振动俘能器的2倍左右。Wang等[10］提出了一种基于弹性放大器的双稳态压电振动俘能器，在典型双稳态压电振动俘能器的基础上在底部加装了弹簧，用以放大外部激振力来跃过势阱壁垒。实验结果表明，在激励频率为17.5 Hz的外部激振力下，该俘能器的输出功率为6.76 mW，是线性压电振动俘能器的26倍。Zhou等[11］将用以构造非线性系统的外部固定磁铁的个数由1个改为3个，通过构造四稳态压电振动俘能器来提高弱外部激励下的能量转换效率。结果表明，该四稳态压电振动俘能器较双稳态压电振动俘能器能更轻松地跃过势阱壁垒，从而大幅拓宽俘能器的有效带宽且增大输出电压。Lallart等[12］将用以构造非线性系统的外部固定磁铁的个数由1个改为5个，进一步提高能量转换效率。另一部分学者通过改良悬臂梁的几何结构来提高俘能器输出性能。刘星[13］等利用圆柱形梁替代传统悬臂梁，使其能采集到二维平面内任意方向的振动能量，其最大输出电压和输出功率分别可达11.6 V和13.5 μW。马天兵[14］等提出了一种Z型压电振动能量收集装置，在低频范围内能集中更多模块，拓宽采集频带，其最大开路电压和输出功率分别为14 V和0.18 μW。Chaudhuri等[15］提出了一种穿孔倒梯形悬臂梁压电振动俘能器，通过选择合理的孔位以及尺寸，相较于使用同尺寸矩形压电振子的俘能器，其固有频率降低27.5%，最大输出电压提高97%。Zhang等[16］提出一种拨动拉拽间接激励式压电振动俘能器，将传统的间接激励方式由拨动式改成拨动拉拽式，该结构的有效带宽是同尺寸单悬臂梁振子压电振动俘能器的4.2倍。

上述研究能够有效提高俘能器的输出电压并拓宽工作频带，但是俘能器的可靠性和环境适应性还存在一些不足。首先，它们的压电振子振动方向与环境方向一致，环境振幅过大时，压电振子的振幅会随之增大，最终导致因变形过大而损毁；其次，它们的压电片与悬臂梁直接连接，压电片在工作过程中易受交变的拉压应力而损毁；最后，它们的压电振子工作频率大多较高，而现实环境中的振动通常频率较低、频带较宽，并且可能存在高强度大振幅的振动[17-18］，例如人或动物运动（约1 Hz）、大型工程机械振动（<10 Hz）及车辆振动（<20 Hz）等。

本文提出一种换向激励式压电振动俘能器（Piezoelectric Vibration Harvester with Excitation Direction Conversion， PVHEDC），它由拾振器和换能器组成。其中，拾振器可以拾取环境振动，产生与环境同向的振动，通过磁力换向机构使换能器产生方向与之垂直的振动，从而将响应振幅控制在安全区域。其优势在于可靠性高、环境适应性强，易于通过调节拾振簧片长度（后称拾振簧片）、拾振簧片附加质量（后称拾振质量）、磁铁间距离等参数改变输出特性和工作频带，实现低频、宽带、高强度及大振幅振动能量回收。通过理论和实验研究了俘能器结构参数、外部激励振幅及负载电阻对输出特性的影响，证明其结构原理的可行性，为振动俘能器的实用化及推广应用提供新思路。

2 结构及原理

换向激励式压电振动俘能器结构原理如图1所示，它由拾振器和换能器组成，两者的振动方向相互垂直。拾振器由激励磁铁、拾振质量以及拾振簧片构成，可以接收环境激励并产生同向的振动。换能器由受激磁铁、端部带顶块的压电振子、换能簧片及换能质量构成，其振动方向与激励方向垂直。拾振器和换能器之间的运动转换通过同性相对安装的磁铁实现。压电振子端部的顶块可实现装配预弯，避免压电振子复位时压电陶瓷因承受过大的拉应力而损毁。

图1 换向激励式压电振动俘能器结构示意图Fig.1 Schematic illustration of Piezoelectric Vibration Harvester with Excitation Direction Conversion， （PVHEDC）

工作过程中，拾振器受激产生与外部激励同方向的振动，两磁铁间的相互位置及磁力发生变化，从而迫使换能簧片带动其两侧的压电振子产生单向弯曲变形发电。换能器的振幅与两磁铁在y轴方向上的位置关系有关。随着磁铁距离在y轴上的分量增大，磁力先增大后减小。当拾振器振幅在一定范围内时，换能器所受激振力随拾振器振幅的增加而增大；超过阈值时，换能器所受激振力及振幅增幅较小或基本不变，从而实现响应振幅，更适于高强度、大振幅的振动场合。此外，改变拾振器和换能器的梁长和附加质量均可以调整俘能器的谐振频率和输出电压，且换能器的振动方向与附加质量所受的重力方向垂直，附加质量的影响较小，拾振器可加的附加质量大于传统的压电悬臂梁，故可通过选用低刚度的梁和较大的附加质量大幅度降低固有频率、增大调频范围、拓宽工作频带。

3 理论建模

为便于建模仿真分析，将图1所示的俘能器简化为图2所示的弹簧-质量-阻尼系统。图2中M1/M2，C1/C2及K1/K2分别表示拾振器和换能器的等效质量、等效阻尼及等效刚度，P（t）=Z0M1ω2cosωt，为拾振器系统的惯性力，ω为激振角频率；F（t）为磁耦合力，Fy（t）和Fz（t）分别为F（t）在y方向和z方向上的分力。

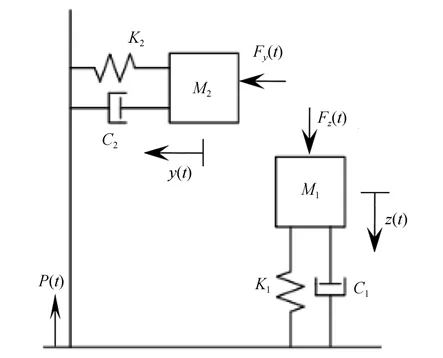
图2 压电振动俘能器的动力学等效模型Fig.2 Dynamic model of piezoelectric vibration harvester

根据振动分析理论，系统的振动微分方程为[19］：

根据刚度计算方法[20］，拾振器的等效刚度为：

式中：E，l1，a1及b1分别为拾振簧片的杨氏模量、长度、宽度及厚度。

根据磁耦合力的计算方法[21］，激励磁铁与受激磁铁间磁力在z方向的最大径向分量Fzm为：

式中：µ0为真空磁导率，M为磁力矩，Lx，Ly，Lz分别为激励磁铁和受激磁铁间距离在x轴，y轴及z轴方向的投影。

由于工作过程中磁耦合力与磁铁间距离以及重叠面积有关，时域上Fz(t)可近似视为正弦函数，即：

根据式（1）~式（4）得拾振器的响应幅值和振幅放大比分别为：

上述公式表明，俘能器的幅频特性由拾振簧片长度l1、拾振质量m1、俘能簧片长度l2、俘能质量m2、磁铁尺寸及间距等参数决定。因拾振器不装配压电振子，其参数可调节性更高，故以它为例，通过仿真研究其质量和刚度/梁长对其幅频特性的影响。为获得拾振器相关结构参数对俘能器输出性能的影响规律，利用Matlab软件进行仿真分析，相关参数如表1所示。

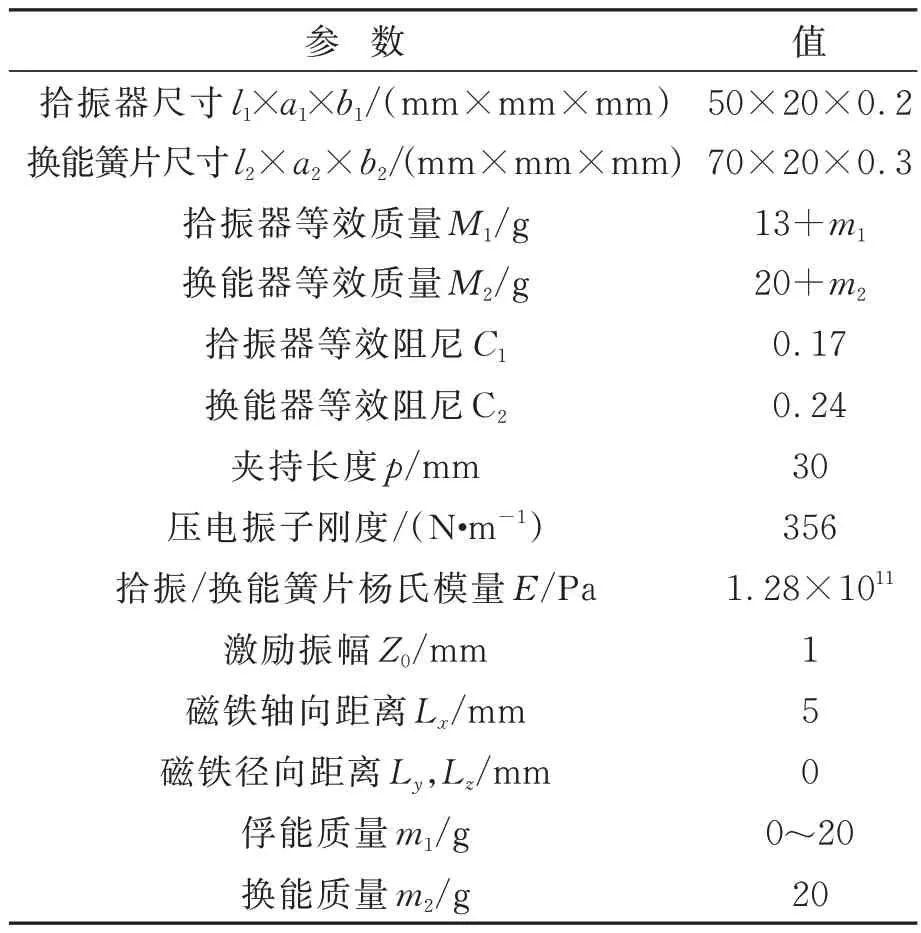
表1 俘能器仿真参数Tab.1 Related parameters for harvester simulation

图3为拾振簧片长度l1不同时俘能器的幅频特性曲线。从图3可以看出：l1不同时均存在两阶谐振频率（fn1和fn2）使得振幅放大比最大（β1和β2）。l1主要影响fn1，随着l1的增大，fn1降低，β1波动较小，fn2基本不变，β2逐渐减小。产生这一现象的原因为：l1增加时拾振器的刚度降低，固有频率降低。由此推断，fn1和fn2分别为拾振器和换能器的固有频率。

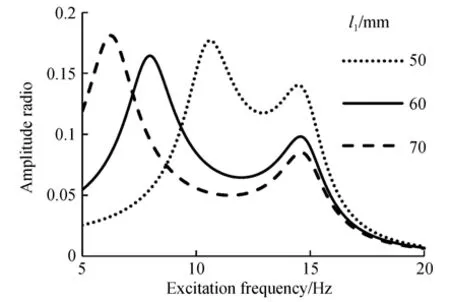
图3 拾振簧片长度不同时俘能器的幅频特性曲线Fig.3 Amplitude ratio of harvester versus excitation fre⁃quency under different elastic beam lengths

图4为拾振质量m1不同时俘能器的幅频特性曲线。由图可知，m1主要影响fn1，随着m1的增加，fn1降低，β1波动不大；fn2基本不变，β2减小。故还可通过调节m1来调节俘能器的工作频带。

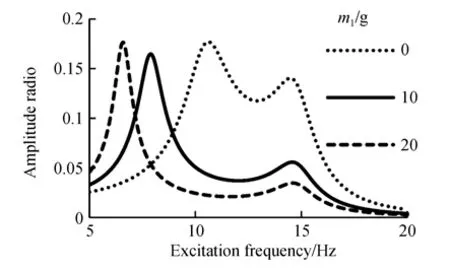
图4 拾振质量不同时俘能器的幅频特性曲线Fig.4 The amplitude ratio versus excitation frequency under different proof mass

综上可知：换向激励式压电振动俘能器为两自由度系统，存在两阶谐振频率使得振幅放大比最大，fn1和fn2分别为拾振器和换能器的固有频率。其中，fn1随l1和m1的增大而降低。fn1和fn2相差越大，俘能器的有效带宽越宽；fn1和fn2越接近，β1和β2越大。故可通过改变拾振器的结构参数使换能器适应低频、宽带的工作环境。

4 实验测试与分析

为验证换向激励式压电振动俘能器原理的可行性及其输出性能与相关参数的关系，设计制作了图5所示的试验样机及测试系统。主要仪器为RC-2000信号控制器、SA-15功率放大器、DC-1000振动台（工作频率为5~2 000 Hz，最大负载为9 800 N，最大位移为±25 mm、最大加速度为12g）、MSO6014A 型混合信号示波器等，激励信号为正弦激励波。拾振器和换能器的参数与仿真（表1）相同，压电振子及磁铁参数如表2所示。实验中所提到的输出电压均为压电振子电学并联后直接测量的开路电压。

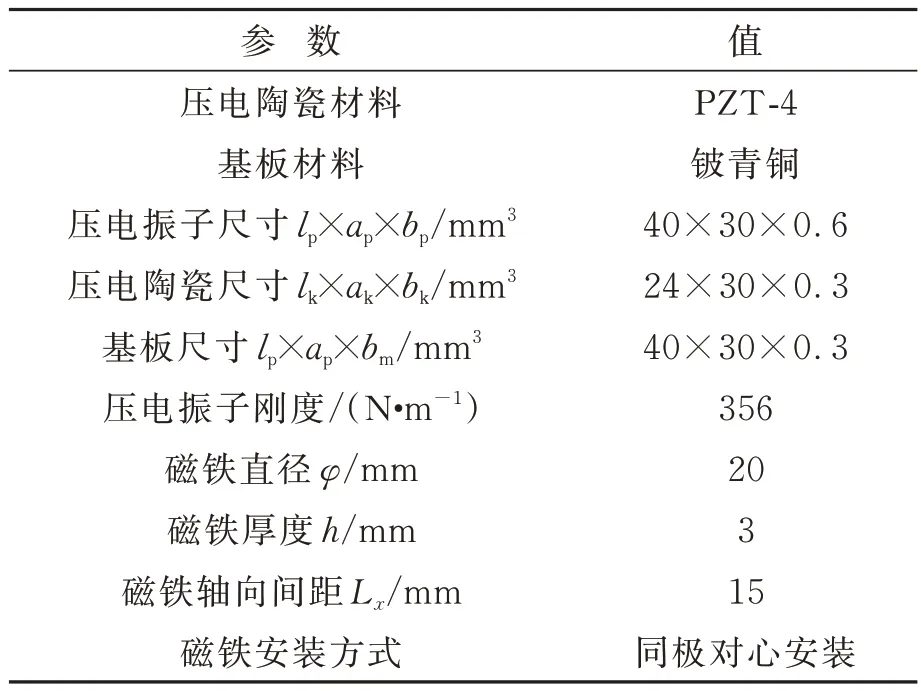
表2 压电振子及磁铁的参数Tab.2 Related parameters for piezoelectric vibrator and magnet

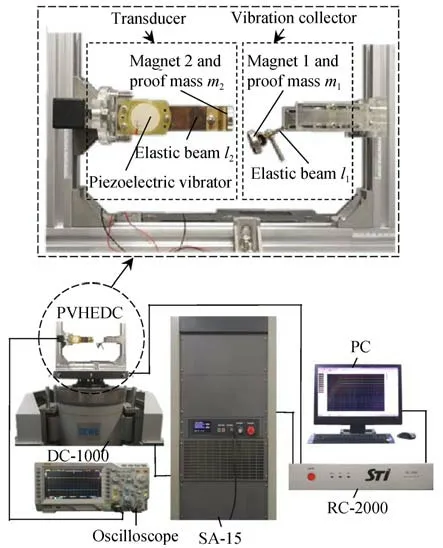
图5 俘能器样机及测试系统Fig.5 Schematic diagram of harvester prototype and ex⁃perimental setup

实验中，为验证俘能器在高强度、大振幅工作环境中的可靠性，测试了外部激励振幅对俘能器输出性能的影响；为验证俘能器低频、宽带工作环境的适应性，测试了拾振长度和拾振质量对俘能器输出特性的影响；为进一步探究俘能器的输出性能，研究了其输出功率特性。

图6给出了外部激励幅值Z0不同时输出电压的幅频特性曲线，图7给出了输出电压与外部激励振幅Z0的关系曲线。由图可知，在不同Z0下均存在两阶谐振频率使输出电压达到峰值。当Z0<3 mm时，随着Z0的增大，两阶谐振频率均小幅减小、输出电压增大；当Z0超过阈值（Z0≥3 mm）时，两阶谐振频率小幅减小、但输出电压增幅较小或基本不变。由压电振子特性可知，其输出特性与变形量相关，故可知当超过阈值时，随着Z0的增大，压电振子的变形量增幅较小或不变。原因在于换能器（压电振子）的变形量与作用在其运动方向上的激振力（磁力）有关。由式（3）可推论出磁力在y方向上的分量随着磁铁间距离的增大先增大后减小，即存在最大值。故换向激励式压电振动俘能器可有效防止压电振子因形变过大而损坏，适于高强度、大振幅的振动环境。

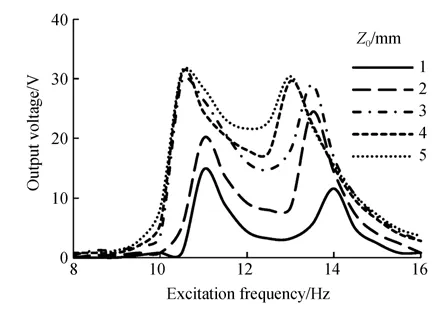
图6 激励振幅不同时输出电压的幅频特性曲线Fig.6 Generator voltage versus excitation frequency un⁃der different excitation amplitudes

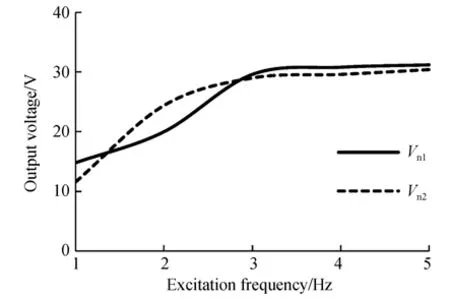
图7 输出电压与外部激励振幅的关系Fig.7 Generator voltage of PVHEDC under different ex⁃citation amplitudes

图8为拾振簧片长度l1不同时输出电压的幅频特性曲线，图9为两阶谐振频率（fn1和fn2）及其所对应的输出电压（Vn1和Vn2）与l1的关系曲线。由图可知，在不同l1下均存在fn1和fn2使俘能器的输出电压出现峰值。当l1为50，55，60，65，70 mm时，fn1和Vn1分 别 为11.5，11，10.5，10，10 Hz和28.8，31.2，25.2，23.2，15.6 V，fn2和Vn2分别为13，13，13，13，13 Hz和34.8，30，21.2，20，14.8 V。由此可知：l1增大时，fn1随之降低，fn2不变，Vn1和Vn2均随之减小。fn1为拾振器的固有频率，fn2为换能器的固有频率。实验结果与仿真分析结果一致，验证了仿真结果的正确性。

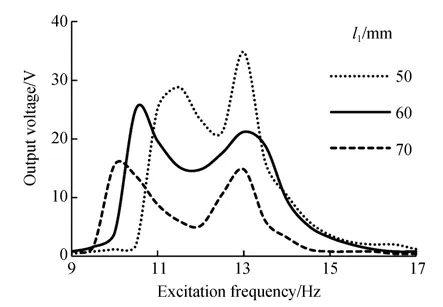
图8 拾振器簧片长度不同时输出电压的幅频特性曲线Fig.8 Generator voltage versus excitation frequency un⁃der different elastic beam lengths

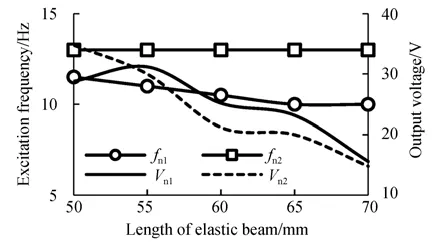
图9 谐振频率及输出电压与拾振簧片长度的关系Fig.9 Resonant frequency versus generator voltage un⁃der different elastic beam lengths

图10给出了拾振质量m1不同时输出电压的幅频特性曲线，图11给出了谐振频率及输出电压与m1的关系曲线。由图可知，在不同m1下均存在fn1和fn2使俘能器的输出电压出现峰值。当m1为0，5，10，15，20 g时，fn1和Vn1分 别 为11.5，10，10，9，8.5 Hz和28.8，28，20.4，26.8，31.6 V，fn2和Vn2分别为13，12.5，13，13，13 Hz和34.8，21.2，19.6，22.4，22.4 V。由此可知：m1增大时，fn1随之减小，fn2基本不变，Vn1和Vn2的波动较小。再一次证明了fn1为拾振器的固有频率，fn2为换能器的固有频率，验证了仿真结果的正确性。

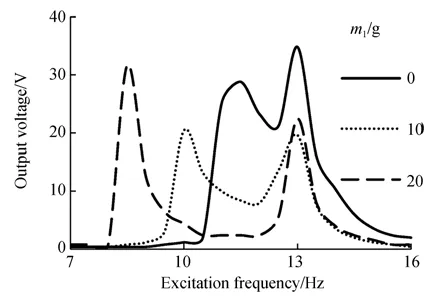
图10 拾振质量不同时输出电压的幅频特性曲线Fig.10 Generator voltage versus excitation frequency un⁃der different proof mass

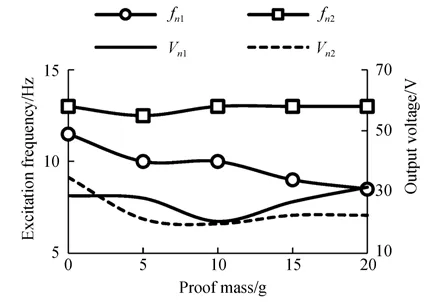
图11 谐振频率及输出电压与拾振质量的关系Fig.11 Generator voltage versus excitation frequency un⁃der different proof mass

图12给出了拾振质量m1不同时输出功率P与负载电阻RL的关系曲线。由图可知：RL不变时，P随m1的增大而减小；m1不变时，P随RL的增大，先增大后减小。当m1=0 g，负载电阻R=540 kΩ时，最大输出功率为0.4 mW。表3比较了几种压电振动俘能器的输出特性，结果表明，PVHEDC不仅能有效控制响应振幅，还拥有理想的输出性能。

图12 拾振质量不同时输出功率与负载电阻的关系Fig.12 Output power of PVHEDC versus load resis⁃tance under different proof wass

表3 现有的部分压电振动俘能器性能Tab.3 Performances of some piezoelectric harvesters

5 结 论

为提高压电振动俘能器对低频、宽带、高强度及大振幅等振动环境的适应性，本文提出了一种PVHEDC，并对其输出性能与相关参数的关系进行了数值仿真与实验研究。结果表明：在一定范围内，俘能器的输出电压随外部激励振幅的增加而增大，当超过阈值时，俘能器的输出电压增幅较小或基本不变。这说明在环境激励振幅过大时，磁力换向结构能有效控制压电振子的变形量（振幅），提高其可靠性，可适应高强度、大振幅的工作环境。该两自由度系统存在两阶谐振频率使俘能器输出电压出现峰值，一阶谐振频率为拾振器的固有频率，二阶谐振频率为换能器的固有频率。两阶谐振频率相差越大，俘能器的有效频带越宽；两阶谐振频率越接近，换能器谐振时的输出电压越高。随着拾振簧片长度和拾振质量的增加，拾振器的谐振频率逐渐减小，换能器的谐振频率基本不变。存在较佳的结构参数使俘能器同时获得较大的输出电压和较宽的频带，因此PVHEDC适应低频、宽带的工作环境。最佳负载电阻RL=540 kΩ时，俘能器的输出功率最大，为0.4 mW。输出功率随拾振质量的增加而减少，随负载电阻的增大先增大后减小。