考虑烧蚀表面形貌影响的气动特性精确预示方法

苏 伟，董 超，薛 普，刘文伶，杨天鹏

考虑烧蚀表面形貌影响的气动特性精确预示方法

苏 伟，董 超，薛 普，刘文伶，杨天鹏

（北京航天长征飞行器研究所，北京，100076）

高速飞行器在飞行过程中防热层烧蚀形成的粗糙表面会影响飞行器的气动特性。针对该问题，对烧蚀表面的近壁流动数值模拟方法进行了研究。采用等效砂粒粗糙度和粗糙函数相结合的方法，对粗糙表面形貌以及对边界层湍流流动的影响进行表征。基于高速粗糙平板风洞试验，开展了3种粗糙壁面湍流模型的数值模拟和验证。最后，以10°尖锥标模外形开展了不同壁面粗糙条件下的流场数值模拟，分析了壁面粗糙对气动特性的影响。研究结果表明，壁面粗糙会对法向力系数、轴向力系数和压心系数产生较大的影响。

烧蚀表面；近壁流动；数值模拟

0 引 言

高速飞行器具有强机动、超远程、强突防等特点，是当前世界航空航天强国研究的重点方向[1]。高速飞行器在大气层内飞行时，气动热环境严酷，防热材料表面受气动加热作用会发生烧蚀，使表面变得粗糙。这种粗糙表面会影响边界层的流动特性，产生气动特性预示偏差。对于长时间大气层内巡航飞行的飞行器，气动预示偏差中轴向力预示偏差的时间积分效应更加显著，易导致航程预示散差大的问题，严重制约飞行器性能的提升，因此须对烧蚀粗糙表面流动特征进行研究，发展高效的数值模拟方法，提高飞行器气动预示精度。

Cebeci等[2]通过修正内层的混合长度值引入粗糙壁面影响。Wilcox等[3]在-量方程模型的基础上修改了涡耗散方程的边界条件；Spalart等[4]在原始S-A模型的基础上进行修正，提出Boeing和ONERA两种湍流模型粗糙修正方法，与试验结果对比吻合较好；Hellsten和Laine[5]对-SST湍流模型的限制器进行了修改，取得了较好的模拟效果；Knopp等[6]在-SST模型的基础上也进行了粗糙修正方法研究；刘通[7]研究了粗糙度对表面摩阻系数、斯坦顿数和升力系数的影响。

目前关于粗糙壁面流动的研究主要针对的是低速不可压缩流动和高速可压缩边界层转捩问题，对于高速可压缩流动湍流问题研究较少。因此本文将对高速粗糙表面流动模拟方法进行研究，并分析壁面粗糙对气动特性的影响。

1 烧蚀表面形貌表征方法

1.1 等效砂粒粗糙高度

高速飞行器多采用非金属热防护材料，烧蚀形成粗糙的典型烧蚀形貌如图1所示。为了便于描述，本文采用Nikuradse[8]提出的等效砂粒粗糙度方法。该方法建立了等效砂粒粗糙高度s与粗糙单元形状参数的关系式，并作为不同粗糙度的统一度量，适用于大面积的粗糙表面流动模拟。

图1 阿波罗11号返回舱防热层烧蚀形貌[9]

Fig.1 Ablation Morphology of the Thermal Protective Layer of Apollo 11 Re-entry Capsule[9]

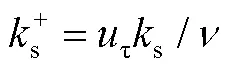
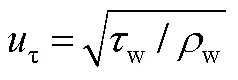
1.2 粗糙函数

图2 湍流速度亏损

无量纲公式为

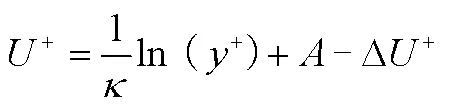
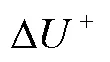
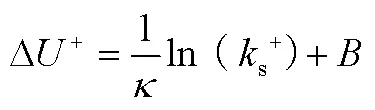
基于式（1）和式（2）可以得到粗糙壁面的壁面律为

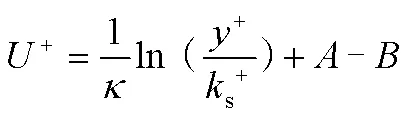
通常认为粗糙壁面形貌给定后，粗糙函数为常数。Nikuradse给出的粗糙函数公式为

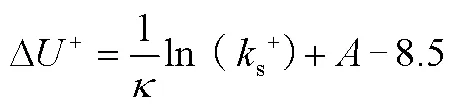
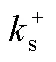
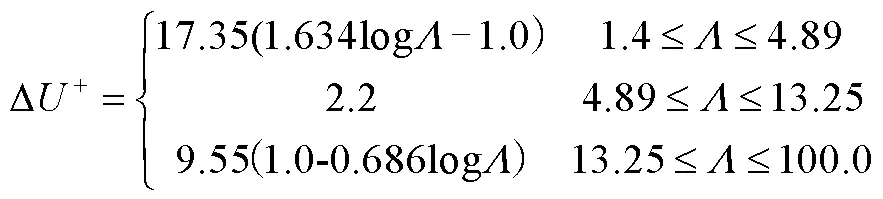
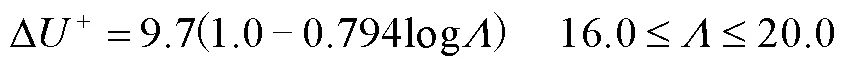
其中式（6）和式（7）分别适用于2D和3D粗糙元情况，3D粗糙元对波阻的影响小于2D粗糙元，因此曲线相对2D粗糙元下移，且

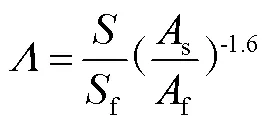
式中为光滑壁面（无粗糙元）的面积；f为表面所有粗糙单元迎风面的总面积；f为单个粗糙元的迎风投影面积；s为单个粗糙元的迎风浸润面积。在该式中，/f为粗糙度密度参数，f/s为粗糙度形状参数。

2 粗糙壁面湍流模型

2.1 B-L零方程湍流模型

B-L模型由内外两层组成，内层遵循Prandtl-Van Driest模型，外层遵循Clauser模型：

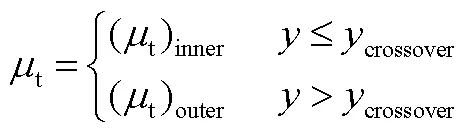
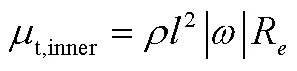
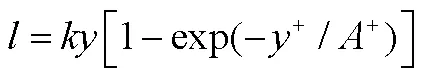
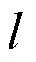
2.2 S-A一方程湍流模型

S-A一方程湍流模型公式为

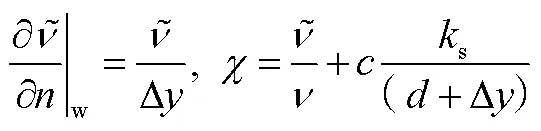
式中 Δ=0.03s。

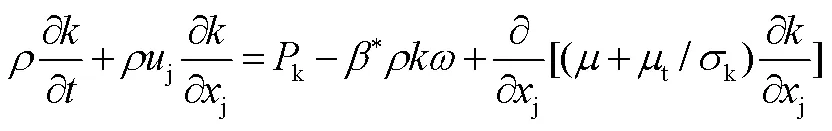
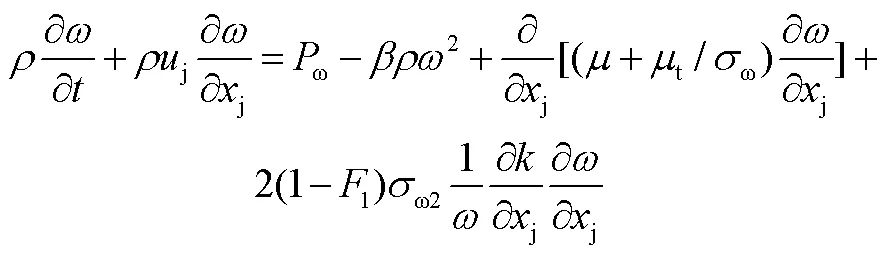
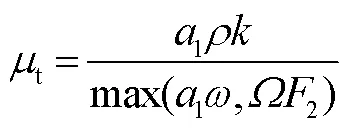
对于光滑壁面，湍流能量方程采用狄里克莱边界条件，湍流扩散速率方程采用Menter[12]提出的边界条件：

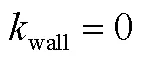
式中 下标1表示靠近壁面第1层网格格心处的值。

对于粗糙壁面，湍流能量方程边界采用与光滑壁面相同的狄里克莱边界条件，Wilcox[3]湍流扩散速率方程中对涡耗散率进行了修正以提高近壁面的涡粘系数：

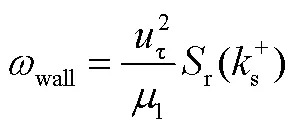
r的值根据Schlichting试验数据得到：

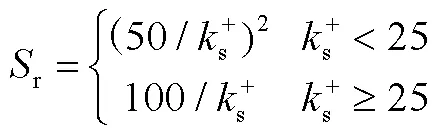
为了防止公式中的限制器在接近壁面时被启用，Hellsten等[5]在以上公式基础上增加混合函数3进行了如下修正：

3 计算结果与分析

3.1 控制方程

数值模拟控制方程是三维Navier-Stokes方程。在直角坐标系下，无量纲化积分形式的Navier-Stokes方程为

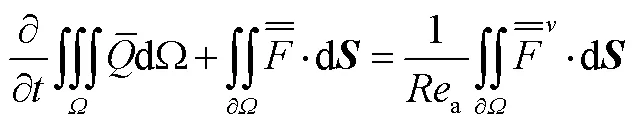
3.2 高速平板

采用Ekoto等[13]高速平板风洞试验对粗糙壁面湍流模型的计算精度进行验证。该试验在德州农工大学高速风洞完成，自由来流马赫数为2.86，总压和总温分别为690 kPa和313 K，壁温w=292 K。模型由有机玻璃加工而成。粗糙壁面模型粗糙元为立方体，通过加工0.79 mm深的沟槽产生。图3给出了风洞试验模型粗糙元示意图。试验在沿流向=159 mm，298 mm和413 mm 3个站位处进行了测量。

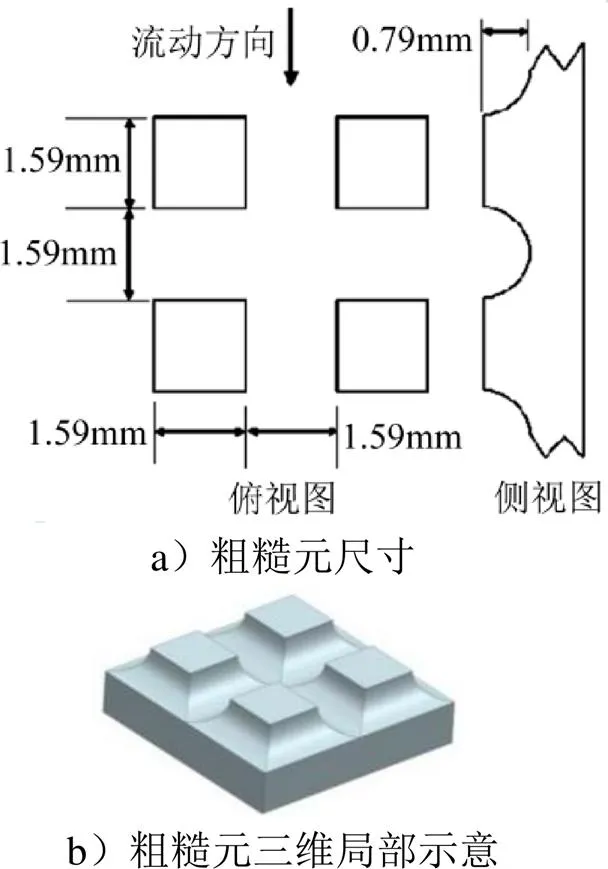
图3 风洞试验模型[13]

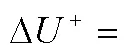
根据Morkovin假设，通过Van Driest变化，可压缩流动速度剖面将与不可压缩流动速度剖面相似。基于密度的Van Driest变换公式如下：

图4至图6给出了不同x站位处的速度剖面对比曲线。可以看出，不同湍流模型数值计算的结果偏差较小，且与风洞试验结果吻合较好。在对数率区域，粗糙平面的剖面曲线相对光滑平面下移，下移值在12.4左右。

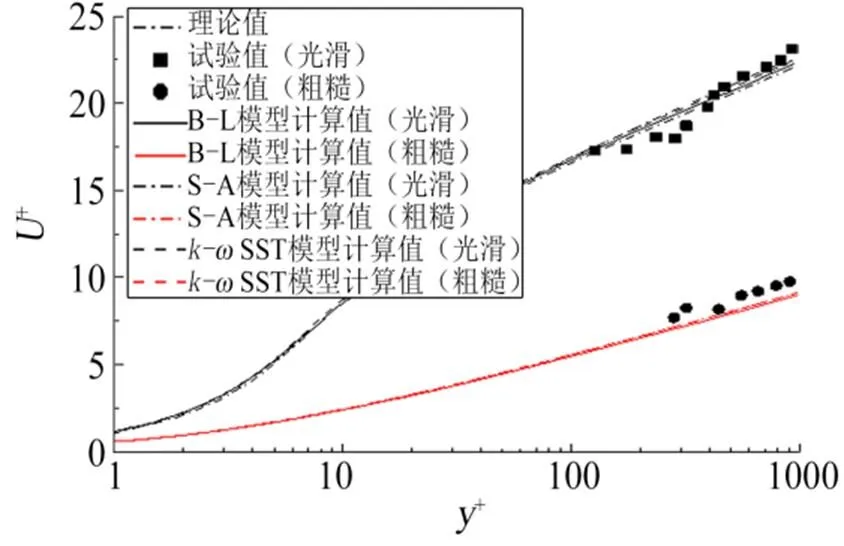
图5 速度剖面（x=298mm）

图6 速度剖面（x=413mm）

图7、图8给分别给出了光滑壁面和粗糙壁面不同站位的速度剖面。从图中可以看出，经过变换后，不同站位的速度剖面相差很小。

图7 光滑壁面不同站位速度剖面

图8 粗糙壁面不同站位速度剖面

3.3 10°尖锥标模

图9 计算网格

图10至图12给出了不同壁面粗糙条件下的轴向力系数、法向力系数和压心系数cp曲线。

图10 轴向力系数CA曲线

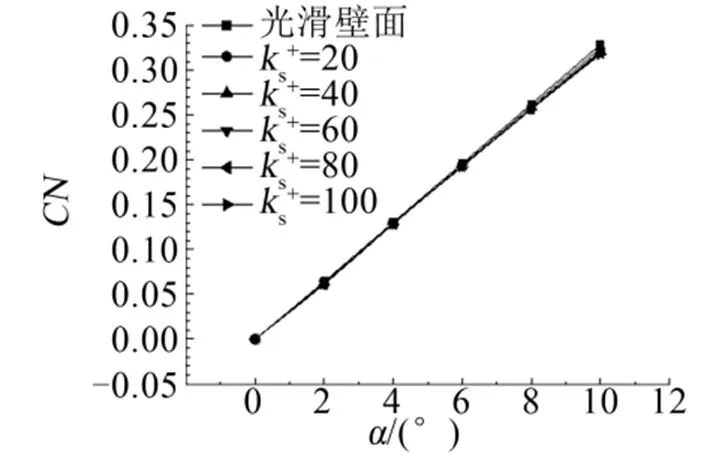
图11 法向力系数CN曲线

图12 压心系数Xcp曲线

从图10至图12中可以看出，在不同攻角下，随着表面粗糙度增加：

a）轴向力系数增大，但是增大幅度会随着s的增大而逐步变小。当s+=100时，攻角0°条件下，轴向力系数比光滑壁面增大了约8.6%，攻角10°条件下，轴向力系数增大了约15%；

b）法向力系数会变小，当s+=100时，攻角0°条件下，法向力系数比光滑壁面减小了约3.3%。法向力系数曲线随攻角变化的斜率也会变小；

4 结 论

本文针对飞行器烧蚀粗糙表面流动数值模拟方法进行了研究。基于粗糙平板风洞试验，对比分析了考虑粗糙表面影响的3种湍流模型的计算精度。基于10°尖锥外形，进行了不同等效砂粒粗糙度条件下的气动特性计算，分析了表面粗糙对气动特性的影响。研究结论如下：

a）3种湍流模型计算的速度剖面与风洞试验结果基本一致。

b）表面粗糙度增加对法向力系数、轴向力系数和压心系数均产生较大影响。

c）表面粗糙度增加会使轴向力系数增大，法向力系数减小，同时使得压心位置前移。

[1] 安复兴, 等. 高超声速飞行器气动设计中的若干关键问题[J]. 中国科学, 2021, 51(10): 104702-1-104702-20.

An Fuxing, et al. Key issues in hypersonic vehicle aerodynamic design[J]. Chinese Science, 2021, 51(10): 104702-1-104702-20.

[2] Tuncer Cebeci, Chang K C. Calculation of incompressible rough-wall boundary-layer flows[J]. AIAA Journal, 1978, 16(7): 730-735.

[3] Wilcox D C. Reassesment of the scale-determing equation for advanced turbulence models[J]. AIAA Journal, 1988(26): 1299-1310.

[4] Aupoix B, Spalart P R. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness[J]. International Journal of Heat & Fluid Flow, 2003, 24(4): 454-462.

[5] Hellsten A, Laine S. Extension of the k-omega-SST turbulence model for flows over rough surfaces[C]. New Orleans, LA: AIAA -97-3577, 22nd Atmospheric Flight Mechanics Conference. August 1997.

[6] Tobias Knopp, Bernhard Eisfeld, Javier Bartolome Calvo. A new extension forturbulence models to account for wall roughness[J]. International Journal of Heat and Fluid Flow, 2009(30): 54–65.

[7] 刘通, 蔡晋生, 屈崑. 壁面粗糙度湍流扩展模型及流动数值模拟[J]. 航空动力学报, 2018, 33(8): 1981-1989.

Liu Tong, Cai Jinsheng, Qu Kun. Roughness for wall turbulence extension model and flow numerical simulation[J]. Journal of Aerodynamics, 2018, 33(8): 1981-1989.

[8] Nikuradse J. Laws of flows in rough pipes[R]. NACA-TM1292, 1950.

[9] Olaf Marxen, Gianluca Iaccarino. Transitional and turbulent high-speed boundary-layers on surfaces with distributed roughness[C]. Orlando, FL: 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, 2009.

[10] Dvorak F A . Calculation of turbulent boundary layers on rough surfaces in pressure gradient[J]. American Institute of Aeronautics & Astronautics, 1969, 7(9): 1752-1759.

[11] Sigal A, Danberg J E. New correlation of roughness density effect on the turbulent boundary layer[J]. AIAA Journal, 1990, 28(3): 554-556.

[12] Menter F R. Two-equation Eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[13] Ekoto I W, et al. Supersonic boundary layers with periodic surface roughness[J]. AIAA Journal, 2015, 46(2): 486-497.

Study on Numerical Simulation Method of Near Wall Flow onAblated Rough Surface

Su Wei, Dong Chao, Xue Pu, Liu Wen-ling, Yang Tian-peng

(Beijing Institute of Space Long March Vehicle, Beijing, 100076)

During the flight of high-speed flight vehicle, the ablation of the heat shield will form rough surface, which will affect the aerodynamic characteristics of the vehicle. The numerical simulation method of near wall flow on ablated surface topography and boundary layer flow is characterized by the combination of equivalent sand roughness and roughness function. Based on the supersonic rough plate wind tunnel experiment, three numerical simulation methods of rough wall turbulence model are used to simulate flow field and be verified. Finally, taking the 10 degree conical standard model as the research object, the flow field simulation under different rough wall conditions is carried out, and the influence of wall roughness on aerodynamic characteristic parameters is analyzed. The results show that the wall roughness has a great impact on the normal force coefficient, the axial force coefficient and the pressure center coefficient.

ablated rough surface; near wall flow; numerical simulation

2097-1974(2023)01-0021-05

10.7654/j.issn.2097-1974.20230105

V211.3

A

2022-09-06；

2022-09-14

苏 伟（1979-），男，博士，研究员，主要研究方向为空气动力学设计。

董 超（1984-），男，博士，研究员，主要研究方向为飞行器总体设计。

薛 普（1990-），男，博士，高级工程师，主要研究方向为飞行器设计。

刘文伶（1963-），女，研究员，主要研究方向为空气动力学设计。

杨天鹏（1993-），男，博士，工程师，主要研究方向为空气动力学设计。