沿驻点线化学非平衡程度评估方法

杨天鹏，严东升，于江鹏，郭 阳，刘文伶

沿驻点线化学非平衡程度评估方法

杨天鹏，严东升，于江鹏，郭 阳，刘文伶

（北京航天长征飞行器研究所，北京，100076）

为了研究高温真实气体效应中的化学非平衡的程度，针对球头的沿驻点线流动，通过高温高压气体的化学反应历程估算化学反应特征时间，使用正激波流动关系来估算流动特征时间，建立了化学非平衡评估模型，给出了化学非平衡程度随马赫数和高度的变化关系。计算结果表明，马赫数越大、高度越低，化学反应特征时间比流动特征时间越小，定义的化学反应特征时间与流动特征时间量级相当时为化学非平衡流动，时间比大于10则接近化学冻结流，时间比小于0.1则接近化学平衡流。在设定的球头模型下，化学反应平衡流在高度0km、10km、20km、30km、40km分别需要马赫数大于8.0、9.5、10.8、12.7、20.0，化学反应冻结流在高度30km、40km、50km、60km分别需要马赫数小于8.4、10.2、12.9、17.5，中间来流状态对应化学反应非平衡状态。

数值模拟；高温真实气体效应；化学非平衡

0 引 言

飞行器在大气中高速运动时，其前缘附近产生的强激波会使得激波层内的空气处于高温高压状态，此时空气会发生一系列复杂的化学反应和能量变化，这种现象被称为高温真实气体效应。对于高温真实气体绕流，一般可将流动分为3种情况[1]：第1种是冻结流，此时流场中的化学反应速率为零，气体组元的组成不随空间和时间变化，但粘性流动会使得气体组元由于扩散而改变；第2种是平衡流，此时流场中的气体处于热力学平衡状态，且流体处于化学平衡状态，此时流场中的化学反应速率为无穷大；第3种是非平衡流，流场中气体的热力学性质和化学反应状态随时间空间发生变化，此时化学反应或能量变化的特征时间与流动特征时间处于相近量级。

对于高温真实气体效应中涉及到的化学平衡态问题，在多个文献中都给出了大致的参考[2,3]，但是这些文献并没有对平衡态问题进行定量分析。文献[4]认为可以通过达姆科勒数am，用于描述同一系统中化学反应相比其他现象的相对时间尺度，使用粒子碰撞特征时间与流场特征时间尺度之比来定义流动的化学状态。但是该定义是一种宽泛的定性认识，一般认为特征时间之比高于4个量级后才能被划分到另一流态，不便于工程应用。由于化学反应与组元构成、能量输运、化学反应机理等等密切相关，并且流动中还需要关注湍流、边界层、壁面催化、烧蚀等一系列与化学反应相耦合的问题，其表现出强烈的非线性，建模难度非常高，难以给出明确的公式对其进行计算。

为了给出高温真实气体效应中对化学非平衡程度的评估，本文从化学反应的宏观表现出发，使用高温高压空气的化学反应历程时间与流动特征时间作为比较，建立化学非平衡评估模型，给出化学非平衡程度随高度和马赫数的变化规律，为流场化学反应模型选取、非平衡流场计算结果不确定度等研究提供参考，提升高速飞行器气动特性预示能力。

1 沿驻点线化学反应流动特征分析

为了定量地建立空气化学反应非平衡程度评估模型，需要首先对相应流场的物理特征进行分析。本文选取化学非平衡程度最为严重的驻点线区域作为评估对象，使用数值模拟方法对化学反应效应和流动特征进行分析。

本文使用多组元可压缩雷诺平均Navier-Stokes方程作为控制方程，其积分形式[5]为

计算模型选用半径50 mm的球头，网格量为100×100，计算网格如图1所示。边界设置上来流为远场边界，物面使用无滑移、绝热壁和非催化壁边界条件，排除物面模型对流动非平衡程度的影响。来流组元为空气，使用Gupta给出的5组元六反应模型及其化学反应速率系数[6]，化学反应模型如表1所示。

图1 计算网格

表1 化学反应方程

Tab.1 Chemical Reaction Equation

序号化学反应方程式 1O2+M=2O+M 2N2+M=2N+M 3NO+M=N+O+M 4N2+O=NO+N 5NO+O=O2+N 6N2+N=2N+N

下面给出高度30 km条件下，分别为10、15、20的3种情况下沿驻点线化学反应能量释放情况。这里定义反应的化学反应功率密度E为

式中 fi为化学反应i的净反应速率；ΔHi为化学反应i的焓变。通过该表达式可以得知在空间中某化学反应所造成的产热功率，其反映了某化学反应对流场内能的影响程度，正值为吸热，负值为放热。从图2中可以看出，不同来流马赫数下，化学反应流场表现出不同的能量释放模式，在Ma=10的情况下，化学反应吸热主要以O2分解为主；在Ma=15的情况下，开始出现NO分解；在Ma=20的情况下，NO分解与O2分解并重，且N2分解反应也表现出较高的吸热量。这说明在评估化学非平衡时，需要同时将O2、N2和NO 3个组元选为评估指标。

续图2

图3给出了=15情况下沿驻点线压强、温度和速度分布。可以看到，沿驻点线的压强在激波后略有升高，基本上保持不变。激波后温度由于激波层较窄，首先呈现出化学冻结的高温，之后由于空气分解吸热导致温度逐渐降低，最后形成一个变化较小的温度平台。而激波后的速度则呈现出接近直线的分布。激波后流动参数分布的规律性使得后文中建立的化学反应非平衡评估模型更加接近于物理实际情况。

图3 Ma=15算例沿驻点线流动参数分布

续图3

2 化学反应特征时间评估

根据上文分析得到的沿驻点线流动特征，本文使用密闭容器中的化学反应进程来评估化学反应特征时间。容器内的起始温度和压强取来流总温和总压，随着反应进程的进行，容器内的温度逐渐降低，该模型与图3给出的沿驻点线上流动参数变化过程较为接近。

图4给出了取=15、高度30 km条件下的组元变化历程，给出了以O2、N2和NO为参考，组元浓度分别达到80%、90%和99%平衡状态情况下的时刻位置。可以看到将化学反应特征时间定义为容器中的氧气和氮气达到80%平衡状态时的反应时间较为合适，之后化学反应处于反应缓慢的平台区，化学反应导致的组元变化和能量变化主要集中于前80%部分，若选择更高的非平衡标准会使得化学反应特征时间成倍增加，化学非平衡评估模型的敏感性降低。

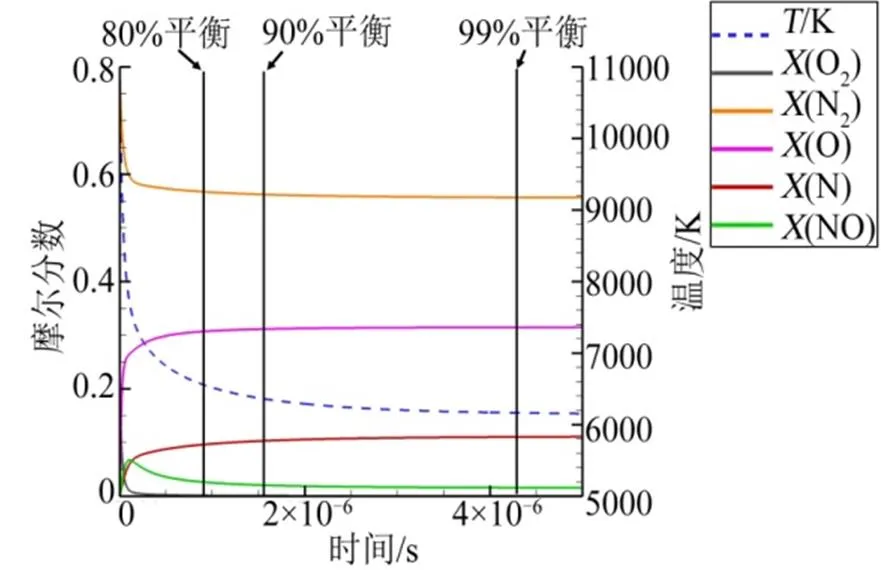
图4 Ma=15算例沿驻点线组元变化历程

图5给出了化学反应特征时间随马赫数和高度的变化关系，可以看到，马赫数越大、高度越低，化学反应特征时间越小，这主要是由于压强和温度增加有助于分子碰撞，从而有利于化学反应进行。但是压强增加并不总有利于空气化学反应进行，可以看到=12附近的曲线会出现转折，在转折两侧的曲线斜率发生了明显变化。这是由于压强增加会增大空气化学反应中各组元的浓度，使得分解反应难以进行，出现局部温度压强增大并不促进化学反应发生的现象。

图5 化学反应特征时间

3 流动特征时间评估

本文以流体微团沿驻点线从正激波后运动到物面的时间为流动特征时间。首先对激波脱体距离进行估算，球头激波脱体距离近似公式[7]如下：

图6给出了不同高度下流动特征时间随马赫数变化情况，由图6可知，在本文所使用的模型中，马赫数对流动特征时间起主导作用，不同高度的流动特征时间变化不大，其整体上表现出随着马赫数增大而减小的趋势。

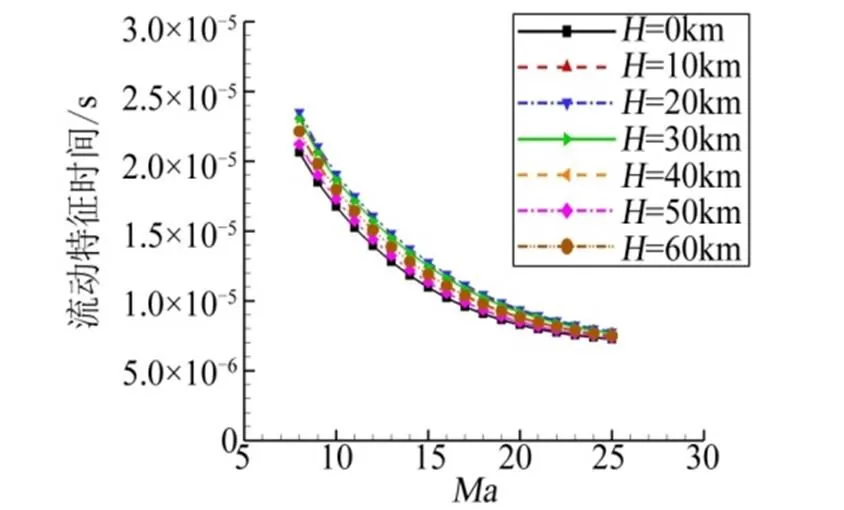
图6 流动特征时间

4 化学非平衡程度模型

本文将化学非平衡定义为化学反应特征时间与流动特征时间处于相近量级，图7给出了化学反应特征时间与流动特征时间之比随马赫数的变化。可以看到，由于不同高度下的流动特征时间较为接近，因此化学非平衡程度整体变化情况与化学特征时间模型基本一致。对于不同高度，高度越高，流动越接近于化学冻结流，这是由于低压使得化学反应更难发生，化学反应时间更长；而对于低高度，流动越接近于化学平衡流，这是由于高压促进分子碰撞，使得化学反应时间更短。

图7 化学反应特征时间与流动特征时间之比

下面进一步对比实际情况与建模之间的不同。为方便起见，选择高度40 km、马赫数为10、13、20的来流参数进行计算，其化学反应特征时间与流动特征时间之比分别为12.3、1.13和0.094。图8给出了沿驻点线不同组元摩尔分数分布的对比，其中0D代表化学反应特征时间的评估结果，其零时间对应于激波面，右侧终点为达到80%平衡的时间。从图8中可以看到，对于=10的情况，流动接近于化学冻结流，组元整体变化程度较小；对于=13的情况，流动处于明显的化学平衡态，且在接近物面处组元的分布恰好接近于平衡态，可以认为此时化学反应时间与流动时间基本相当；对于=20的情况，可以看到沿驻点线组元很快达到了平衡态，流动接近于化学平衡流。由于本文采用了正激波模型，因此数值模拟得到的结果相比于建模结果，其激波后温度较低，化学反应速率较低。

图8 沿驻点线组元变化历程与非平衡建模结果对比

续图8

以上3个算例对比说明本文所建立的化学非平衡程度评估模型是可行的，可以用于指导化学非平衡数值模拟。对于流动中化学非平衡的判据则需要根据数值模拟的需要进行，从结果来看，化学反应特征时间比流动特征时间的值取为0.1～10之间可以认为是化学非平衡，大于10则接近化学平衡流，小于0.1则接近化学冻结流。需要注意的是，在低马赫数下化学非平衡程度呈现出向化学平衡流移动的趋势，但是此时流场中的温度不够高，高温真实气体效应不明显，即使是化学非平衡流也可使用化学冻结流模型进行计算。

由于前缘半径与激波脱体距离近似成正比关系，前缘半径越大沿驻点线的流动特征时间越长，但化学反应特征时间是不具有几何相似性的，因此前缘半径越大，化学反应特征时间比流动特征时间越小。实际飞行器前缘半径的取值与本文所选数值不会有量级上的差异，相比于化学反应特征时间约3～4个量级的跨度，前缘半径改变带来的时间变化相对较小。

5 结 论

本文针对球头绕流中的驻点线流动，通过高温高压气体的化学反应历程给出了化学反应特征时间，使用正激波流动关系来估算流动特征时间，建立了化学非平衡评估模型，通过化学反应特征时间与流动特征时间之比给出了流场中的化学非平衡程度随马赫数和高度的变化结果，并通过数值模拟结果验证了非平衡评估结果的正确性。可用于指导高速流动中的化学反应模型选取。

计算结果表明，化学反应特征时间随马赫数增大而减小，随高度增加而增加；流动特征时间随高度变化不大，随马赫数增大而减小；化学反应特征时间与流动特征时间之比与化学反应特征时间规律相近，其随马赫数增大而减小，随高度增加而增加。与数值模拟结果对比表明，时间比处于0.1～10之间可以认为是化学非平衡，大于10则接近化学冻结流，小于0.1则接近化学平衡流。在本文设定的球头模型下，化学反应平衡流在高度0 km、10 km、20 km、30 km、40 km分别需要马赫数大于8、9.5、10.8、12.7、20.0，化学反应冻结流在高度30 km、40 km、50 km、60 km分别需要马赫数小于8.4、10.2、12.9、17.5，中间来流状态对应化学反应非平衡状态。

[1] 欧阳水吾, 谢中强. 高温非平衡空气绕流[M]. 北京: 国防工业出版社, 2001.

Ouyang Shuiwu, Xie Zhongqiang. High temperature non-equilibrium flow[M]. Beijing: National Defence Industry Press, 2001.

[2] Miller J H. Computational aerothermodynamic datasets for hypersonic heat transfer on reentry vehicles[C]. San Francisco: AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2005.

[3] Tauber M E, Meneses G P. Aerothermodynamics of transatmospheric vehicles[C]. Boston: 4th Thermophysics and Heat Transfer Conference, 1986.

[4] 中国科学院. 中国学科发展战略新型飞行器中的关键力学问题[M]. 北京: 科学出版社, 2018.

Chinese Academy of Sciences. Chinese discipline development strategy key mechanical problems in new aircraft[M]. Beijing: Science Press, 2018.

[5] 王江峰, 等. 高超声速复杂气动问题数值方法研究进展[J]. 航空学报, 2015, 36(1): 159-175.

Wang Jiangfeng, et al. Progress in numerical simulation techniques of hypersonic aerodynamic problems[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 159-175.

[6] Gupta R N, et al. A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000K[R]. NASA-RP-1232, 1989.

[7] Anderson J D. 高超声速和高温气体动力学（第2版）[M]. 北京: 航空工业出版社, 2013.

Anderson J D. Hypersonic and high-temperature gas dynamics(Second Edition)[M]. Beijing: Aviation Industry Press, 2013.

Evaluation Method of Chemical Non-equilibrium along Stagnation Line

Yang Tian-peng, Yan Dong-sheng, Yu Jiang-peng, Guo Yang, Liu Wen-ling

(Beijng Institute of Space Long March Vehicle, Beijing, 100076)

In order to study the degree of chemical non-equilibrium in high-temperature real gas effect, this paper begins with the flow of the ball head along the stagnation line to establish a chemical non-equilibrium evaluation model. In this model, the chemical reaction characteristic time is calculated by using the chemical reaction process, and the flow characteristic time is evaluated by using the relationship before and after the normal shock wave. The degree of chemical non-equilibrium variation law with Mach number and height is given. Calculation results show that the larger the Mach number and the lower the height makes the ratio of chemical reaction characteristic time and flow characteristic time smaller. The flow is chemical non-equilibrium when the chemical reaction characteristic time and flow characteristic time is in the near order of magnitude. If the time ratio is greater than 10, the flow is close to the chemical equilibrium flow, and if the time ratio is less than 0.1, the flow is close to the chemical frozen flow. Under this ball head model, the chemical equilibrium flow requires Mach numbers greater than 8.0, 9.5, 10.8, 12.7, and 20.0 at heights of 0 km, 10 km, 20 km, 30 km, and 40 km respectively. The chemical frozen flow requires Mach numbers less than 8.4, 10.2, 12.9, and 17.5 at heights of 30 km, 40 km, 50 km, and 60 km respectively. The intermediate inflow state is chemical non-equilibrium flow.

numerical simulation; high-temperature real gas effect; chemical non-equilibrium

2097-1974(2023)01-0122-05

10.7654/j.issn.2097-1974.20230124

V211.3

A

2022-11-09；

2022-12-04

杨天鹏（1993-），男，博士，工程师，主要研究方向为飞行器气动设计。

严东升（1963-），男，研究员，主要研究方向为飞行力学设计。

于江鹏（1995-），男，博士，工程师，主要研究方向为飞行器气动设计。

郭 阳（1991-），男，博士，工程师，主要研究方向为飞行器气动设计。

刘文伶（1963-），女，研究员，主要研究方向为飞行器总体设计。