泵喷宽带非定常激振力预报与参数分析*

武星宇，王 东，魏应三，靳栓宝，祝 昊，胡鹏飞，孙方旭

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

水下泵喷推进器噪声一直以来被国内外许多学者关注和研究[1]，其噪声分为空化噪声和无空化噪声。空化噪声是水面舰船泵喷推进器的主要特性，而对于强调隐声性能的潜艇而言要避免其产生空化噪声，因此，无空化噪声是潜艇推进器主要噪声[2]。从噪声源上分析，泵喷推进器无空化噪声源在频域上一般分为两部分:离散激振力源分量和宽频激振力源分量。船尾伴流与泵喷推进器互作用产生离散激振力源，入流湍流与泵喷推进器互作用产生宽带激振力源[3]。随着离散激振力源被抑制，宽频激振力源成为泵喷推进器主要噪声源[4-5]。为降低泵喷推进器激振力产生的宽带辐射噪声，深入研究湍流场中泵喷推进器非定常宽频激振力源是很有必要的。

Howe[6]提出一种可计算平板非定常响应的经验模型，但是该模型依赖于实验测量的数据。为预报平板与湍流互作用产生的激振力，Chase[7]通过风洞实验拟合给出一种壁面压力谱经验模型，Ciappi等[8]采用Chase模型预报船体表面的宽频加速度响应谱，并通过拖曳水池实验验证了该模型，然而该经验模型依旧依赖于计算流体力学(computational fluid dynamics, CFD)或实验提供边界层厚度、剪力等参数。Karman等[9]针对二维薄翼模型，考虑薄翼尾流涡的影响，指出尾流涡会诱导薄翼表面产生非定常脉动压力。由此Sears[10]假设薄翼弦长相对波长忽略不计，推导得到著名的Sears传递函数，该函数建立了湍流波与薄翼表面非定常升力之间的关系。在此基础上，Blake[11]应用谱方法推导出螺旋桨宽频噪声计算公式，但由于模型对流场过度简化导致计算误差较大。因此，Sevik[12]提出相关性法计算螺旋桨宽频激振力，并通过水洞实验验证，结果显示计算值与实验值趋势一致，但计算值未能准确地描述宽带噪声在叶频处的峰值。Jiang等[13]将螺旋桨旋转带来的影响考虑在内，分别采用频谱法[11]和相关性法计算螺旋桨非定常激振力，两种方法都能准确地预报螺旋桨非定常激振力在叶频处的峰值，频谱法和相关性法没有本质的区别。蒲汲君等[14]、蒋靖伟等[15]在Jiang的研究基础上分析了螺旋桨和流场参数对宽带非定常激振力的影响。

但与螺旋桨不同的是，泵喷推进器一般采用定转子布置形式[16]，在计算转子宽频辐射声功率时，必须考虑前导叶对预报结果的影响。Nallasamy等[17]针对轴流风扇出口导叶辐射噪声问题，采用Gauss尾流模型模拟转子尾流，建立了转子尾流湍流波数谱模型，结合线性的N-S方程得到风扇出口导叶宽频非定常激振力，通过声类比方程得到出口导叶的辐射声功率，并通过实验进行了验证。Posson等[18]结合Nallasamy建立的转子尾流模型和叶栅响应函数[19]，推导得到风扇出口导叶宽频辐射声功率计算公式，并通过美国国家航天局(national aeronautics and space administration, NASA)实验模型进行了验证。

泵喷推进器定转子布置形式与空气中的轴流风扇相似，均具有定转子结构。为此，本文将从Sears函数出发，结合叶片尾流模型，推导得到泵喷推进器转子宽频非定常激振力，并与数值结果进行对比验证。最后，进一步分析流场参数对泵喷推进器宽频非定常激振力的影响。

1 公式推导与验证

1.1 宽频激振力计算表达式

忽略叶片厚度影响，采用条带法将前导叶和转子沿径向等分为若干条带并在半径R处展开，顺着展向可得到如图1所示的二维模型，图中c为转子叶片弦长，s为转子叶片间距，αs为转子安放角，Ω为转子角速度，α为前导叶安放角，(xs,ys)为固定在转子上的坐标系。

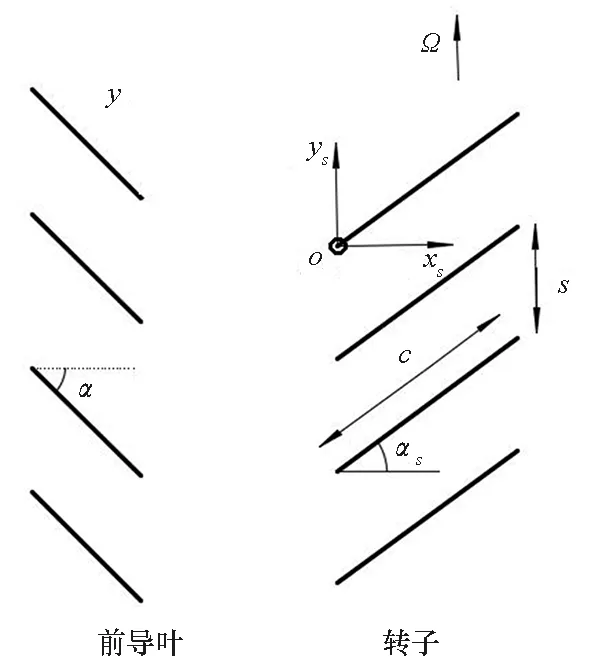
图1 2D前导叶-转子模型Fig.1 2D model of the inlet guide vane and the rotor

当上述图中转子入流为简谐湍流波时，

W·n=W0e-iωt+ikxxs+ikyys+ikzzs

(1)

式中，W为流场中湍流向量，n为叶栅叶片法向向量，W0为简谐湍流波幅值，ω为湍流波角频率，t为时间，kx、ky分别为湍流波在xs、ys方向上的波数，i为虚数单位。Sears[10]针对图1所示的模型，建立了叶片非定常响应与湍流之间的关系，在简谐湍流波条件下，转子叶片表面的非定常激振力为：

P=ρπcW0USe(kxc/2)

(2)

式中，ρ为流体密度，U为平均入流速度，Se为Sears函数，则

(3)

式中，H0和H1分别表示第0阶和第1阶Hankel函数，式(2)表示第二类Hankel函数。

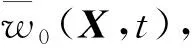
(4)

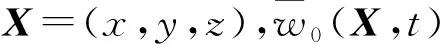
(5)

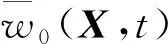
(6)

式中：h0(X-tUxux)为归一化后湍流脉动随时间的变化量，ux为速度向量；g0(X)为湍流脉动随空间的变化量。进一步可得

(7)

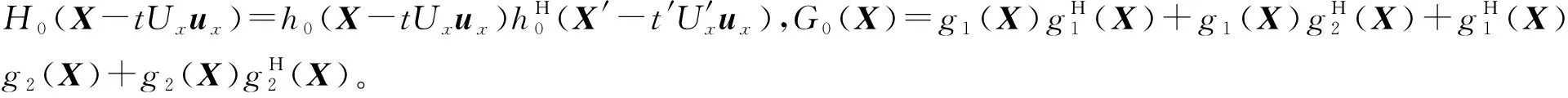
当背景湍流为充分发展的湍流时，有

g1(X)=u1

(8)

式中，u1为背景流湍流平均脉动速度。忽略转子叶片厚度，采用Park-Gauss尾流模型模拟转子叶片尾流， 则：

(9)

式中，u2为转子尾流湍流脉动速度，L为转子叶栅尾流尾迹宽度，sR为转子叶栅叶片间隙。以sRcos(αR)为周期，通过傅里叶级数展开，将式(19)化为如下形式：

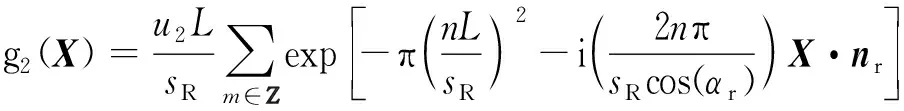
(10)

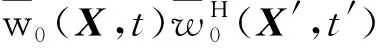
(11)

其中

式中，φ′(K)为单位湍流脉动幅值下的湍流波数谱。 从而可得到考虑前导叶的转子叶栅宽频辐射声功率计算表达式为：

(12)

不考虑旋转泵喷推进器的侧斜和纵倾，其湍流波角频率ω与测试角频率ω0的关系为：

(13)

式中，σ=kxd+kyh为相邻叶片湍流入流相位差，k为整数，Ω为转子角速度，ωRk为由于旋转导致的角频率变化量。 将式(13)代入式(12)可得：

(14)

令kyh=k′yh+2πk可得：

(15)

将叶栅横坐标系转换到柱坐标系，考虑转子的旋转，从而将式(15)化为：

(16)

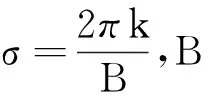
(17)

式中，λ为叶片在半径r处的螺距角。

1.2 湍流谱模型

为计算湍流与叶片互作用产生的非定常激振力，需要对叶片的湍流进行量化。然而螺旋桨或泵喷推进器进流参数的实验测量困难，且目前没有准确的数学模型来描述湍流场。为此Liepmann湍流波数谱、Kerschen湍流波数谱等湍流近似模型被提出[19]。

假设泵喷推进器入流湍流为各向同性均匀，经实验验证Liepmann模型鲁棒性较好且受参数变化的影响较小，此时式(15)中的Φ0为：

(18)

式中，Λ为湍流积分尺度，u为平均脉动速度。

然而实际的泵喷推进器入流湍流涡在泵喷推进器的拉伸作用下会发生轴向畸变，如图2所示。为考虑泵喷推进器的拉伸作用，Kerschen建立了一种轴对称湍流谱模型，其一般形式为：

图2 湍流涡拉伸Fig.2 Diagram of the turbulent vortex tension

(19)

对于无侧斜和纵倾的泵喷推进器有Q21=-sinα，则

(20)

式中，ux、uy分别为泵喷推进器进流湍流在x和y方向上的湍流脉动幅值，Λx、Λy分别为x和y方向上的湍流积分尺度。

2 公式验证

2.1 与螺旋桨实验模型对比

Sevik[12]通过水洞实验对螺旋桨与湍流互作用宽带非定常激振力进行了研究，图3为实验螺旋桨结构示意图。实验螺旋桨叶片数为10，叶片无纵倾和侧斜，螺旋桨叶片弦长恒定为25.42 mm，叶稍半径为101.60 mm，叶根半径为25.00 mm，螺旋桨进速系数为1.22。与本文公式计算相关的螺旋桨工况与入流参数如表1所示。

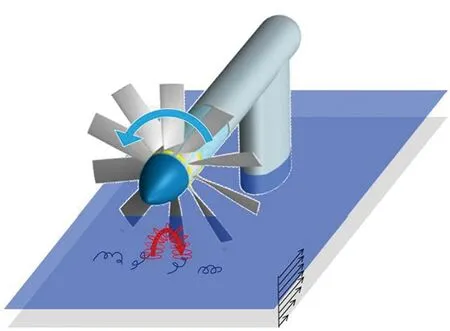
图3 Sevik实验模型Fig.3 Sevik test model

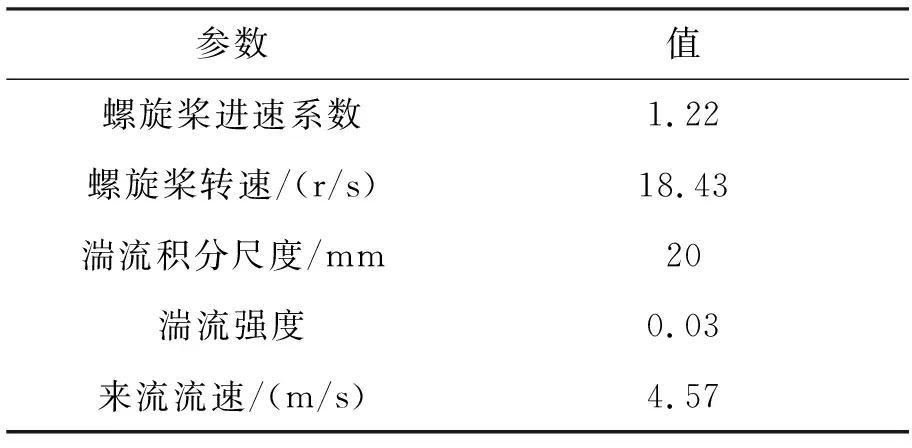
表1 Sevik实验模型静子入流参数Tab.1 Inflow parameters of the Sevik test model

图4为采用本文计算方法得到的非定常激振力和实验值对比。本文方法结算结果包括采用Liepmann湍流波数谱计算结果和采用Kerschen湍流波数谱计算结果。由于缺乏翔实的实验数据，在采用Kerschen湍流波数谱预报螺旋桨非定常激振力时假设ux=uy，对比Λx=0.5Λ和Λy=2Λ工况。

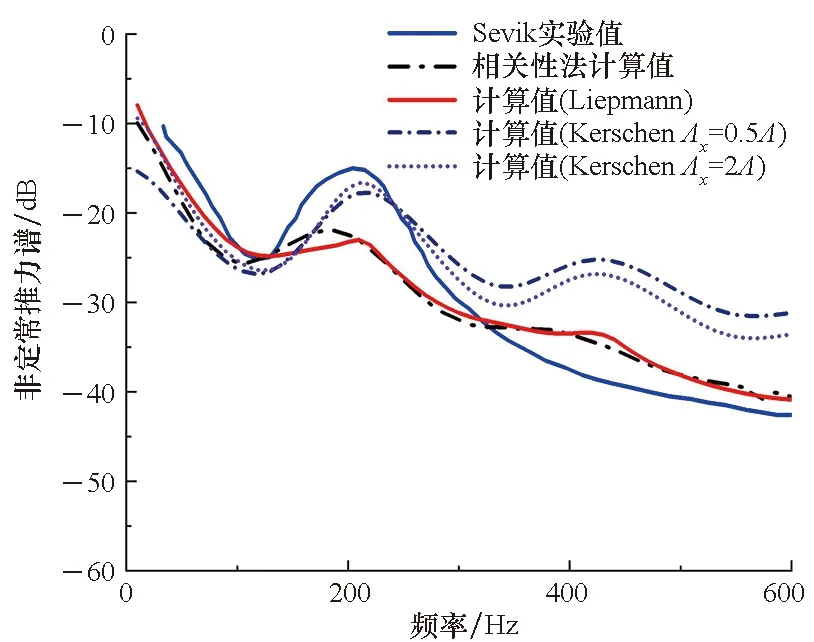
图4 实验值与计算值对比Fig.4 Comparing between test value and calculated value

通过对比可得，在300 Hz以下频率范围，采用Kerschen湍流波数谱模型得到的非定常宽频推力谱与实验值一致，较准确地预报了推力谱在叶频处出现的波峰；在300～600 Hz频率范围，采用Kerschen湍流波数谱模型计算得到的结果与实验值差别较大，这是由于Kerschen湍流波数谱模型依赖于准确的湍流涡参数，通过经验确定的湍流涡参数误差较大。图4中，Liepmann湍流波数谱模型得到非定常激振力谱与相关性法计算得到的结果一致，较准确地预报了推力谱在叶频处出现的波峰。整体而言，在缺乏准确的湍流参数时，在600 Hz以下频率范围，采用鲁棒性较好的Liepmann模型预报得到的螺旋桨非定常宽频推力与实验值误差更小。在2.2节中，将采用Liepmann模型进一步研究具有前导叶的泵喷推进器转子非定常激振力。

2.2 与泵喷推进器数值模型对比

泵喷推进器结构如图5所示，该推进器具有前导叶和转子，其中U为转子平均入流速度，前导叶叶片数为11，转子叶片数为9，转子转速为350 r/min。与本文公式计算相关的推进器参数如表2所示，其中与长度相关的参数通过导管半径进行了无因次处理。

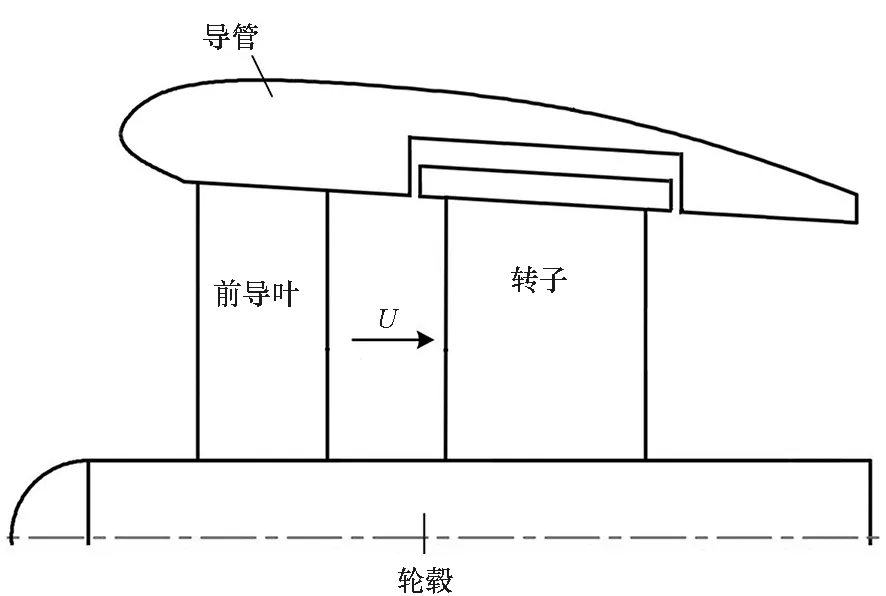
图5 泵喷推进器结构示意图Fig.5 Schematic of pump-jet propeller structure

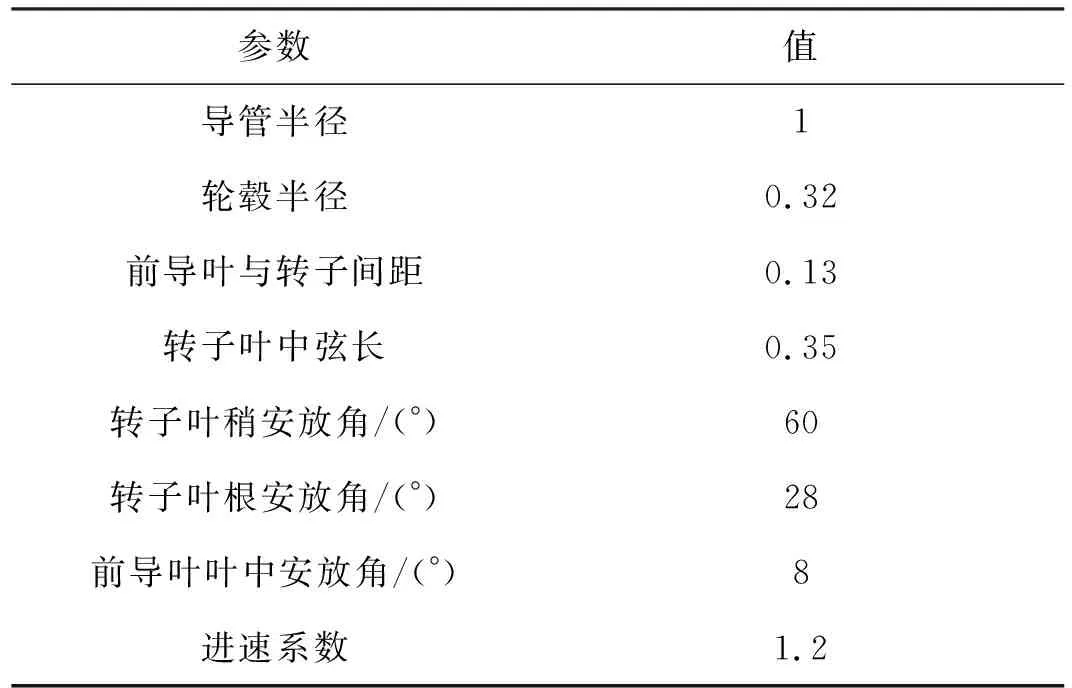
表2 泵喷推进器主要参数Tab.2 Main parameters of the pump-jet propeller

与螺旋桨不同的是，该型泵喷推进器转子工作在前导叶尾流中，在计算时需要考虑前导叶对转子非定常激振力的影响。图6对比了泵喷推进器转子宽频非定常激振力CFD计算结果与本文公式计算结果，由于推进器转速相对图4螺旋桨模型较低，所以泵喷推进器宽带谱的波峰效应不明显。本文公式计算结果包括不考虑前导叶结果和考虑前导叶结果，在采用公式计算时，背景流和前导叶尾流的湍流强度为0.03，湍流积分尺度为Λ/RT=0.03，前导叶尾流的半尾迹宽度通过经验公式确定[20]。通过图6可得，在600 Hz以下频率范围，公式计算得到的泵喷推进器转子非定常激振力与数值计算结果趋势一致，是否考虑前导叶的影响对非定常激振力谱的发展趋势影响不大，但考虑前导叶计算得到的结果在幅值上大于不考虑前导叶的计算结果，这是因为前导叶的影响使得转子进流流场的不均匀度增加，且在上述工况下考虑前导叶的结果与数值计算结果相近。

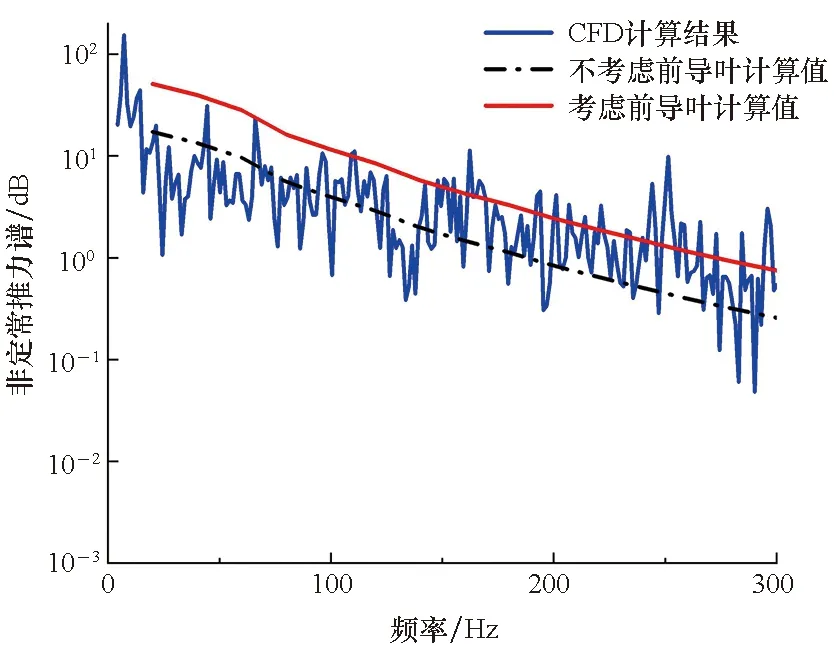
图6 数值计算值与计算值对比Fig.6 Comparing between numerical value and calculated value

为分析湍流参数对泵喷推进器转子非定常宽频激振力预报结果的影响，图7给出了不同湍流强度和湍流积分尺度下的转子非定常激振力谱对比曲线。图7(a)对比了湍流强度I分别为0.01、0.02、0.03、0.04、0.05时泵喷推进器转子的非定常激振力谱。由图7(a)可得，当频率低于600 Hz时，湍流强度越大，转子的非定常激振力也就越大。但是随着湍流强度的增加，非定常激振力的增加幅度逐渐减小。

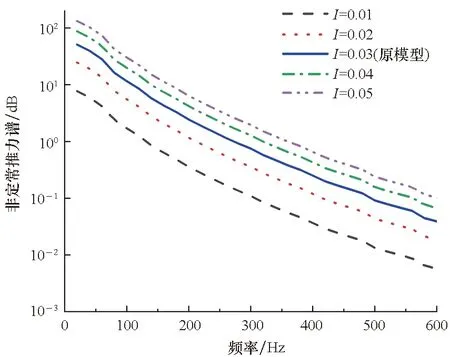
(a) 湍流强度(a) Turbulence intensity

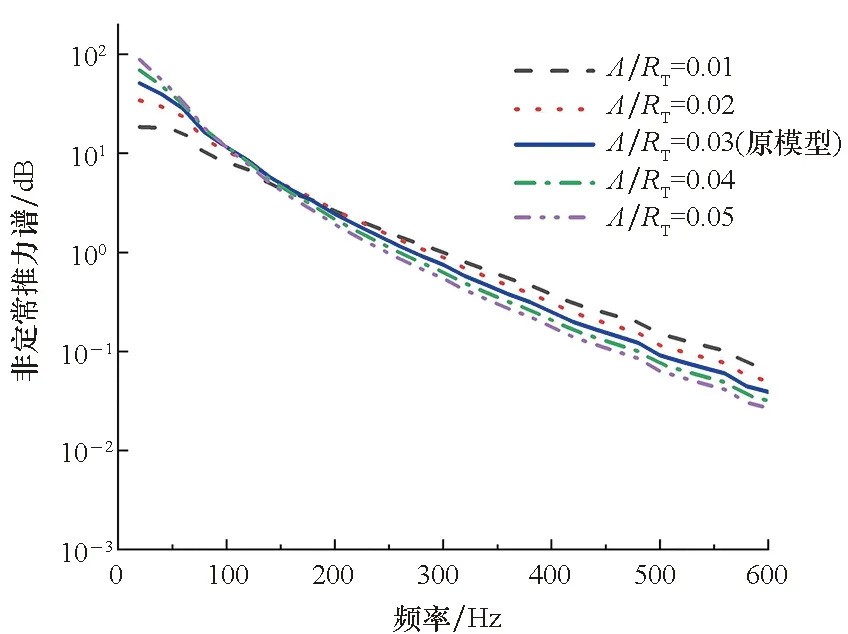
(b) 湍流积分尺度(b) Turbulence integral scale图7 湍流参数对泵喷推进器转子非定常宽频激振力的影响Fig. 7 Influence of turbulence parameters on unsteady broadband unsteady force of pump-jet propeller rotor

图7(b)对比了湍流积分尺度Λ分别为0.01RT、0.02RT、0.03RT、0.04RT、0.05RT时的转子非定常激振力谱，RT为转子叶稍半径。由图7(b)可得，在0～600 kHz频率范围，湍流积分尺度的变化对转子非定常宽频激振力谱随频率的发展趋势有一定的影响，具体表现为：在150 Hz以下频率，湍流积分尺度越大，非定常激振力越小；在150 Hz以上频率，湍流积分尺度越小，非定常激振力越小。但总体来看，湍流积分尺度的变化对泵喷推进器转子的非定常激振力谱的幅值影响较小。

通过图7可得，湍流参数的变化对泵喷推进器转子的非定常激振力有一定的影响，特别是湍流强度对其幅值有很大的影响，这是因为湍流强度越大，转子进流场的脉动速度越大，湍流与叶片的相互作用越强。相对于湍流强度，湍流积分尺度对转子非定常激振力谱的影响较小。

3 分析和讨论

针对2.2节的泵喷推进器模型，采用考虑前导叶尾流作用的转子宽频非定常激振力计算公式分析叶片参数对转子宽频非定常激振力的影响。忽略叶片参数变化对转子入流流场的影响，图8 (a)～(b)分别给出了不同弦长和安放角下泵喷推进器转子的非定常激振力谱。

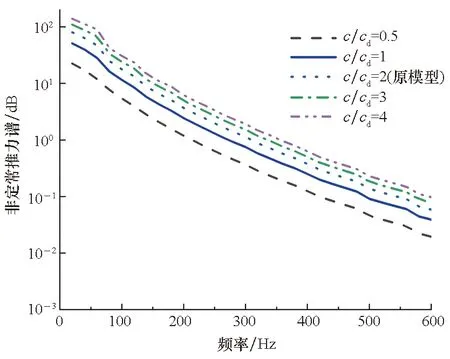
(a) 弦长(a) Chord length

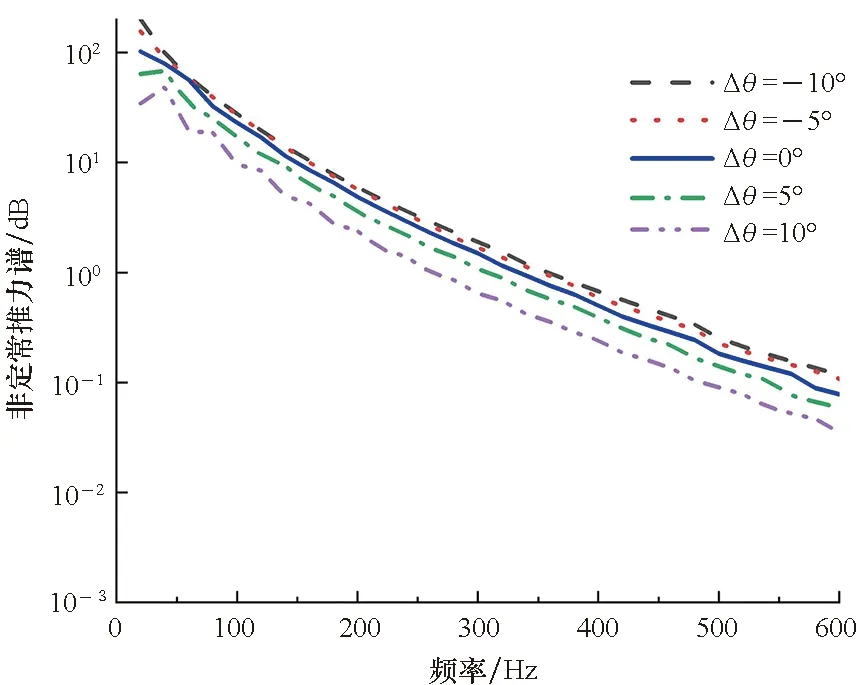
(b) 安放角(b) Stagger angle图8 叶片参数对泵喷推进器转子非定常宽频激振力的影响Fig.8 Influence of blade parameters on unsteady broadband unsteady force of pump-jet propeller rotor

图8(a)对比了弦长c分别为0.5cd、1cd、2cd、3cd、4cd时的转子非定常激振力，cd为原推进器弦长。由图8(a)可得，当频率低于600 Hz时，弦长越长，转子的非定常激振力也就越大。但是随着弦长的增加，非定常激振力的增加幅度逐渐减小，弦长c=0.5cd与c=1cd时的非定常激振力幅值相差最大。

图8(b)对比了安放角变化对转子非定常宽频激振力谱的影响，表示的是转子叶片不同半径处的安放角变化均为Δθ，考虑角度变化对转子入流流速的变化，此时的转子入流流速UΔθ=Ucos(Δθ)。由图8(b)可得，减小5°和10°转子安放角使得转子非定常激振力谱略微增加，但增加幅度较小。增加转子安放角会使得非定常激振力幅值降低，增大10°转子安放角使得非定常激振力幅值减小幅值较大。

4 结论

本文在Sears函数的基础上考虑随机湍流涡与泵喷推进器的相互作用，推导得到螺旋桨宽频非定常激振力频域计算公式，通过与Sevik水洞实验模型对比验证了本文公式，与时域的相关性法比较，两者并不存在本质上的区别。但是，相对于时域的相关性法，频域的计算方法通过结合湍流波数谱模型，能够考虑泵喷推进器转子前导叶对其宽频非定常激振力的影响。通过与泵喷推进器数值模型计算结果对比，验证了本文公式，并通过参数分析得到如下结论：

1)本文公式能够较准确地预报泵喷推进器转子的非定常宽频激振力，但是其预报结果依赖于湍流参数，特别是湍流强度对预报结果影响较大，主要影响其幅值。

2)忽略叶片参数的变化对转子湍流入流的影响，降低转子弦长和增加转子安放角能够在一定程度上减小泵喷推进器转子的非定常激振力。

综上所述，本文解析公式可预报工作在前导叶尾流中转子的非定常宽频激振力。相对于时域的相关性法，从频域的角度能够考虑前导叶的影响，适用于泵喷推进器转子的非定常性能预报与定性的参数研究，为下一步研究泵喷推进器辐射噪声打下基础。但是，本文公式也存在一定的缺陷，由于比较依赖湍流参数，如果需要定量的研究还需通过实验法或数值计算方法提供转子入流参数。