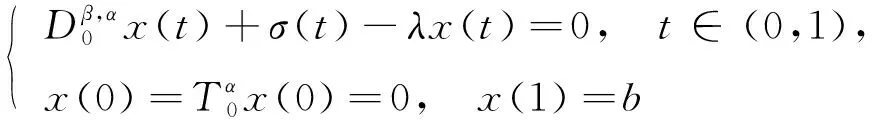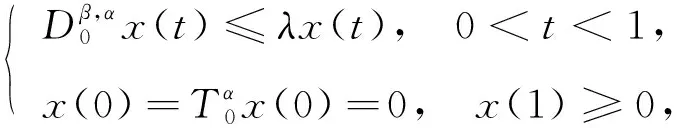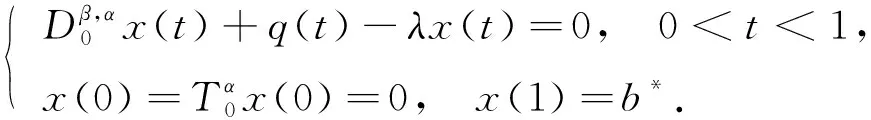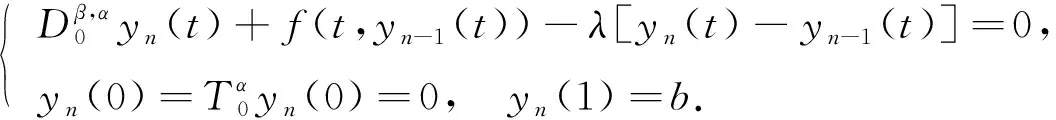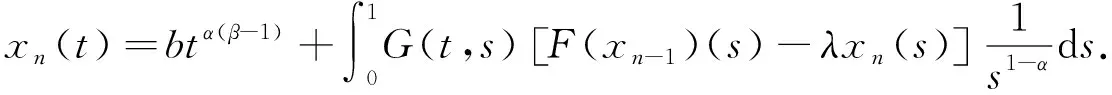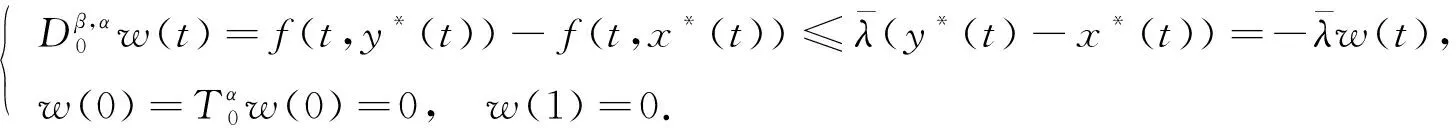一类非线性Riemann-Liouville适型分数阶微分方程正解的存在性
2023-03-09彭钟琪毕国健薛益民
彭钟琪, 李 媛, 毕国健, 薛益民
(1.沈阳工业大学 理学院, 沈阳 110870;2.徐州工程学院 数学与统计学院, 江苏 徐州 221018)
0 引 言
分数阶微分方程在热力学系统、材料与机械系统、控制系统等[1]工程领域应用广泛, 关于分数阶微分方程解的存在性研究目前已取得了许多成果[2-6].单调迭代技巧是研究整数阶和分数阶微分方程初值问题和边值问题的有效工具[7-11].文献[10]研究了如下非线性标准Riemann-Liouville型分数阶微分方程边值问题:
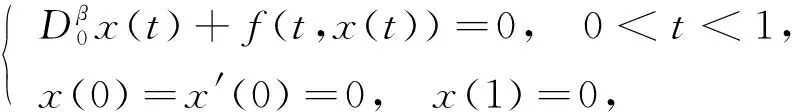
(1)
f(t,y(t))-f(t,x(t))≥-λ[y(t)-x(t)],
其中x0(t)≤x(t)≤y(t)≤y0(t),x0(t),y0(t)分别是问题(1)的下解和上解,λ是一个常数且满足严格的限制条件.
由于分数阶微分算子定义的多样性, 如Riemann-Liouville,Caputo,Hadamard,Caputo-Hadamard型[12-14]等, 因此可选择最合适的算子描述实际应用中的复杂问题[15-20].Jarad等[15]建立了Riemann-Liouville适型分数阶导数和Caputo适型分数阶导数; 文献[17]用Krasnosel’skii’s不动点定理及Leray-Schauder非线性抉择理论等方法研究了一类非线性Caputo适型分数阶微分方程四点边值问题解的存在性和唯一性; 文献[18-19]用单调迭代技巧和上下解法分别研究了一类Caputo适型和Riemann-Liouville适型分数阶微分方程极值解的存在性.
受上述研究工作的启发, 本文考虑如下非线性Riemann-Liouville适型分数阶微分方程边值问题:
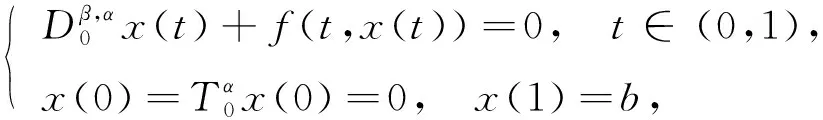
(2)

1 预备知识
定义1[21]函数f: [a,∞)→的α阶左适型导数定义为
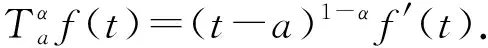
定义2[15]函数f: (a,+∞)→的β阶左Riemann-Liouville适型积分定义为
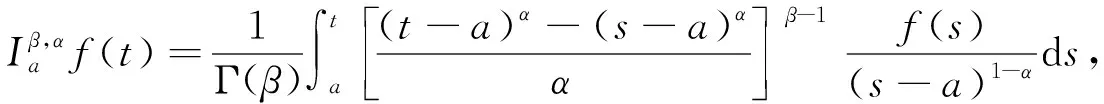
(3)
其中β>0,α∈(0,1].当α=1时, 分数阶积分(3)转化为标准Riemann-Liouville型分数阶积分.
定义3[15]函数f: (a,+∞)→的β阶左Riemann-Liouville适型导数定义为
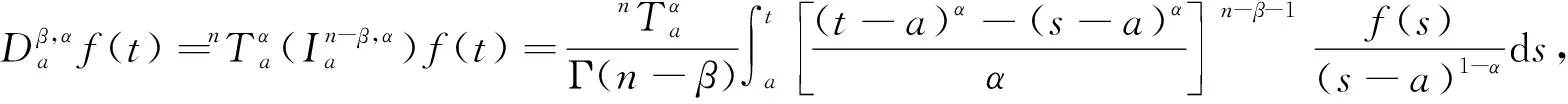
(4)
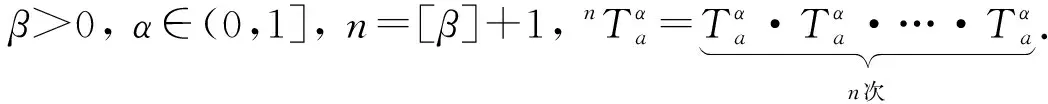
定义4如果函数x0(t)∈C[0,1]满足如下关系:
则x0(t)称为方程(2)的下解.如果函数y0(t)∈C[0,1]满足如下关系:
则y0(t)称为方程(2)的上解.
引理1[15]若β,γ>0,α∈(0,1], 0 引理2[15]若β>0,α∈(0,1], 则 其中ci∈,i=1,2,3,…,n,n=[β]+1. 引理3设h(t)∈C[0,1],α∈(0,1],β∈(2,3], 则边值问题 等价于积分方程 其中 证明: 由引理2知, 方程(5)可化为 由式(6)可得 所以问题(5)-(6)等价于 引理4函数G(t,s)有如下性质: 1)G(t,s)∈C([0,1]×[0,1]); 2) ∀t,s∈(0,1), 有G(t,s)>0; 证明: 性质1)显然成立.下证性质2)~4).当0 所以∀t,s∈(0,1),G(t,s)>0.即性质2)成立. 由性质1)有 所以 即性质3)成立.下证性质4). 当0≤s≤t≤1时, 有 令γ(s)=sα(1-sα)β-1, 证毕. (7) 1) ∀x∈V∩∂Ω1, ‖Ax‖≤‖x‖, 且∀x∈V∩∂Ω2, ‖Ax‖≥‖x‖; 2) ∀x∈V∩∂Ω1, ‖Ax‖≥‖x‖, 且∀x∈V∩∂Ω2, ‖Ax‖≤‖x‖. 引理6设f∈C([0,1]×[0,∞),[0,∞)), 定义算子T:P→E为 青岛市非物质文化遗产与文化创意产业互动发展研究…………………………………………………邢崇,韩凌雯(2,81) 则算子T:P→P是全连续的. 因此T(Ω)一致有界.对任意的x∈Ω, 0≤t1 当t2→t1时, ‖Tx(t2)-Tx(t1)‖→0, 所以T(Ω)是等度连续的.根据Arzela-Ascoli定理, 算子T:P→P是全连续的. 为方便, 记 定理1设b=0,f∈C([0,1]×[0,∞),[0,∞)).若存在常数c≥1,r2>r1>1, 满足下列条件: 1)f0+=0; 2) ∀(t,x)∈[0,1]×[0,r2],f(t,x)≤Mr2; 3) ∀(t,x)∈[0,1]×[0,r1],f(t,x)≥Nr1. 证明: 由于b=0, 故可定义算子A:P→P为 由引理6知算子A:P→P是全连续的, 且算子A的不动点即为问题(2)的解. 由条件1)知, 可选取充分小的η满足 0<η≤M, (8) 从而存在L>0, 满足 f(t,x)≤ηxc,t∈[0,1],x∈[0,L]. (9) 令Ωr3={x∈P: ‖x‖ r3 (10) 由式(8)~(10)和引理4知, ∀x∈P∩∂Ωr3,t∈[0,1], 有 即 ‖Ax‖≤‖x‖, ∀x∈P∩∂Ωr3,t∈[0,1]. (11) 令Ωr2={x∈P: ‖x‖ 即 ‖Ax‖≤‖x‖, ∀x∈P∩∂Ωr2,t∈[0,1]. (12) 令Ωr1={x∈P: ‖x‖ 即 ‖Ax‖≥‖x‖, ∀x∈P∩∂Ωr1,t∈[a1/α,(1-a)1/α]. (13) 下面用单调迭代技巧和上下解方法证明问题(2)极值解的存在性和唯一性.首先给出如下假设. 假设: (H1) 存在常数λ<0, 满足0<-λ (H2) ∀t∈[0,1],x0(t),y0(t)∈P分别是问题(2)的下解和上解, 且x0(t)≤y0(t); (H3) 常数λ满足 f(t,y(t))-f(t,x(t))≥-λ[y(t)-x(t)], 其中x0(t)≤x(t)≤y(t)≤y0(t),t∈[0,1]. 引理7若假设条件(H1)成立, 则∀x(t),σ(t)∈E, 边值问题 (14) 有唯一解. 证明: 由引理3知, 问题(14)等价于积分方程 定义算子S:E→E为 ∀x(t),y(t)∈E, 由引理4可得 即 ‖Sy-Sx‖≤-λM-1‖y-x‖. 由假设条件(H1)和Banach不动点定理可知, 问题(14)有唯一解. 引理8若假设条件(H1)成立, ∀x(t)∈E,x(t)满足如下关系: (15) 则∀t∈[0,1],x(t)≥0. (16) 由式(16)、引理3和引理4可得 令t=t*, 得-λM-1≥1, 与假设条件(H1)矛盾, 因此x(t)≥0. 定理2若假设条件(H1)~(H3)成立, 则问题(2)在区间 [x0,y0]={x(t)∈P:x0(t)≤x(t)≤y0(t)} 上有极值解x*(t),y*(t), 且 0≤x0(t)≤x*(t)≤y*(t)≤y0(t). 证明: ∀t∈[0,1],n=1,2,3…, 定义 (17) (18) 由引理7知x1,y1有唯一解, 下面分三步证明问题(2)有极值解. 1) 证明{xn},{yn}是单调序列.令u(t)=x1(t)-x0(t), 则由式(17)和假设条件(H2)有 由引理8得u(t)≥0, 即x0(t)≤x1(t).类似可得y1(t)≤y0(t).令r(t)=y1(t)-x1(t), 由式(17),(18)和假设条件(H3)有 由引理8得r(t)≥0, 即x1(t)≤y1(t).综上可得x0(t)≤x1(t)≤y1(t)≤y0(t).下面证明x1(t)为问题(2)的下解,y1(t)为问题(2)的上解.由式(17)可得 根据下解的定义知x1(t)为问题(2)的下解, 同理y1(t)为问题(2)的上解.由数学归纳法可得 x0(t)≤x1(t)≤…≤xn(t)≤…≤yn(t)≤…≤y1(t)≤y0(t). 2) 证明xn,yn满足如下关系: (19) (20) 令F(xn)(t)=f(t,xn(t))+λxn(t), 由假设条件(H3)易知函数F连续且单调非增.根据引理3, 式(17)可化为 (21) 由P是正规锥可知{xn}一致有界.根据F,G的连续性, 易知{xn}是等度连续的.由Arzela-Ascoli定理知{xn}满足式(19), 同理{yn}满足式(20).由式(19),(21)和Lebesgue控制收敛定理得 即x*是问题(2)的一个解, 同理y*也是问题(2)的一个解. 3) 证明x*(t),y*(t)是问题(2)的极小解和极大解.假设x(t)∈[x0,y0]是问题(2)的任意一个解, 且满足xn(t)≤x(t)≤yn(t).令l(t)=x(t)-xn+1(t), 由式(16)和假设条件(H3)有 由引理8得l(t)≥0, 即xn+1(t)≤x(t).类似可得x(t)≤yn+1(t).所以xn+1(t)≤x(t)≤yn+1(t).令n→∞, 有0≤x*(t)≤x(t)≤y*(t).证毕. 注2文献[10]利用单调迭代技巧证明了问题(1)存在极值解, 并假设常数λ>0满足如下条件: 3) [Kλ+β2(1-β)2]λ(β-1)2<Γ(β)β2(1-β)2. 而本文只需假设常数λ<0满足 与文献[10]相比, 本文极大简化了λ所需满足的限制条件. 假设: 其中x0(t)≤x(t)≤y(t)≤y0(t),t∈[0,1]. 定理3若假设条件(H1)~(H4)成立, 则问题(2)存在唯一解. 证明: 由定理2知, 问题(2)在区间[x0,y0]存在极值解x*(t),y*(t), 且x*(t)≤y*(t).因此只需证x*(t)≥y*(t)即可. 令w(t)=x*(t)-y*(t).由假设条件(H4)得 (22)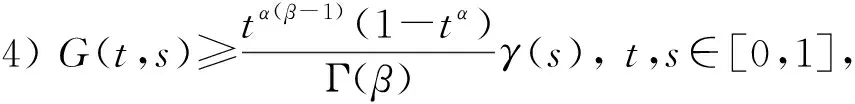
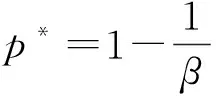
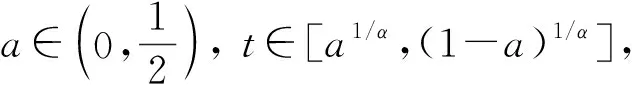



2 正解的存在性
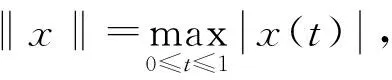
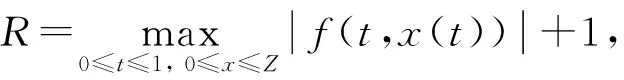
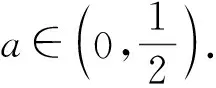
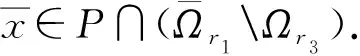
3 极值解的存在性和唯一性