Straight-Path Following and Formation Control of USVs Using Distributed Deep Reinforcement Learning and Adaptive Neural Network

Zhengqing Han,Yintao Wang,and Qi Sun

Dear Editor,

This letter presents a distributed deep reinforcement learning(DRL) based approach to deal with the path following and formation control problems for underactuated unmanned surface vehicles(USVs).By constructing two independent actor-critic architectures,the deep deterministic policy gradient (DDPG) method is proposed to determine the desired heading and speed command for each USV.We consider the realistic dynamical model and the input saturation problem.The radial basis function neural networks (RBF NNs) are employed to approximate the hydrodynamics and unknown external disturbances of USVs.Simulation results show that our proposed method can achieve high-level tracking control accuracy while keeping a desired stable formation.

Employing multiple USVs as a formation fleet is essential for future USV operations [1].To achieve formation,the vehicles can be driven to the individual paths first,then the formation is obtained by synchronizing the motion of the vehicles along the paths.Therefore,the path following and formation control problems are simultaneously studied in this letter.For the path following (PF) task,a USV is assumed to follow a path without temporal constraints [2].Since the route is typically specified by way points,following the straight path between way points is a fundamental task to USVs.It is a challenging issue considering the highly nonlinear systems with time-varying hydrodynamic coefficients,external disturbances and under actuated characteristic.Extensive research has been undertaken to address above problems,such as back stepping control [3],sliding mode control [4],NN-based control [5] and model predictive control [6].Among these methods,RBF NNs [5] have been proven to be a powerful solution for handling model uncertainties and disturbances.

Recently,researchers have shown an increased interest in artificial intelligence (AI) methods,e.g.,DDPG method is used to solve the PF problem.DDPG plays a role of both guidance law and low-level controller in [7],or only acts as a low-level controller in [8].However,these approaches are vulnerable to dynamic environment and cannot realize satisfactory tracking control accuracy.To overcome above problems,a DDPG-based guidance law is presented with an adaptive sliding mode controller in [9],which proves the benefit of DRL strategies in guidance.Therefore,a promising idea is taking advantage of DRL methods to obtain efficient guidance law,then using RBF NNs to achieve high-level control accuracy,while giving the DRL-based approach the ability to deal with model uncertainties and disturbances.That is the first motivation of our work.

Several attempts have been made to the formation control of USVs.In [10],all vehicles are coordinated by consensus tracking control law,but a fixed communication topology is required.To reduce the information exchanges among vehicles,an event-based approach is presented in [11] such that the periodic transmission is avoided.In [12],each robot follows its leader by visual servoing,where some information only needs to be exchanged by an acoustic sensor at the beginning.The study in [13] provides new insights into USV formations by proposing a distributed DRL algorithm,where the adaptive formation is achieved by observing the relative angle and distance between follower and leader,and the plug-and-play capability is obtained by applying a trained agent onto any newly added USVs.However,it does not consider the problems of model uncertainties,unknown disturbances and input saturation.Hence,the second motivation of our work is using a distributed DRL method to achieve adaptive and extend able formation control,while reducing the communication frequency.Similarly,by combining DRL method with RBF NNs,the high-level control accuracy can be achieved.

Based upon the discussions above,our main contributions are: 1) A DDPG-based guidance law is employed to make USVs converge to the desired path,where transfer learning (TL) is utilized to increase the tracking performance;2) The desired formation position of each vehicle is achieved by using a distributed DRL method,and a potential function is presented to realize smooth control;3) RBF NNs are proposed to design the low-level controller for under actuated USVs that subject to the unknown external disturbances,and an adaptive compensating approach is presented to address the input saturation problem.In this letter,the DRL-based approach is utilized to determine the desired yaw rate commandrdand speed commandud,and the NN-based controller is expected to produce the control input forces and torques for tracking the reference signals.The algorithm architecture is depicted in Fig.1.It is shown through numerical examples that our proposed method can achieve satisfactory performance for both path following and formation tasks.

Fig.1.The architecture of the proposed algorithm.

Preliminaries:1) The dynamic model concerned in this work is motivated by [5].The vector η=[x,y,ψ]Tdenotes the position (x,y)and the yaw angleψin the earth-fixed frame.The vector ν=[u,υ,r]Tdescribes the linear velocities (u,υ) and the yaw raterin the body fixed frame.We consider a group of USVs with the same structure.Then,the three-degree-of-freedom model of each vehicle can be described as

Controller design:The system matricesM,CandDare divided into nominal part and bias part,i.e.,M=M∗+∆M,C=C∗+∆CandD=D∗+∆D,where (·)∗denotes the nominal value obtained from the experiment,and ∆(·) denotes the unknown bias part.Thus,the model in (1)can be rewritten aswhereThen,the model can be further rewritten as

Theorem1: Consider the under actuated USV model (2) in the presence of model uncertainties,unknown environmental disturbances and input saturation,together with the controller in (3),and the weight update lawin (4),if the appropriate design parameters are chosen,the surge speed tracking error and the yaw rate tracking error converge to a small neighborhood of the origin,the signals in the closed loop system are uniformly ultimately bounded.

Proof: The proof is omitted due to page limitation.

Path following and formation tasks:As shown in Fig.2,a startpointp k=[xk,yk]Tand an endpointp k+1=[xk+1,yk+1]Tare chosen to construct a straight path in the earth frame.γp=atan2(yk+1−yk,xk+1−xk) is the angle of the path.xe=(x−xk+1)cos γp+(y−yk+1)sin γpis the along-tracking error,andye=−(x−xk+1)sin γp+(y−yk+1)cos γpis the cross-tracking error.Then,for the PF task,the control objective is to makeyeconverge to zero,i.e.,limt→∞ye(t)=0.For the for mation task,the leader-follower strategy is selected,and the speed of leader is assumed to be constant.The desired angle is defined as αpd= αd+γp,where αdis decided by the formation shape.The relative angle tracking error is defined as αe= αp− αpdfor followers on the left,and as αe= αpd− αpfor followers on the right.Then,the control objective of the formation task is to make αeconverge to zero,i.e.,l i mt→∞αe(t)=0.

Fig.2.Geometry of the path following and formation tasks.

For each task,both actor and critic have two hidden layers with 400 and 300 units,respectively.The activation functions for all of the hidden layers are rectified linear units (ReLU).The output layer of the actor has a hyperbolic tangent activation function,and the output layer of the critic has a linear activation function.During training,each episode has 600 training steps,with a time step of 0.05 s.The training of the PFACN and the FACN are run with 3000 episodes and 2000 episodes,respectively.The learning rate is set to 10−4for the actor and to 10−3for the critic.Batches of 128 transitions are drawn randomly from a buffer of size 106,with the discount factor γ=0.99 and the soft target update rate τ=0.001.

Results and discussions:The model uncertainty of USVs can be supposed as ∆( η, ν)=[0.8,0.2r2,0.2u2+sin(v)+0.1vr]T.The disturbances in the earth frame can be defined asω(t)=[0.6sin(0.7t)+1.8cos(0.05t)−2,1.5sin(0.06t)+0.4cos(0.6t)−3,0]T.For controller design,eachSl(Z) has 11 NN nodes.The gain matrices are defined as Γl=4I11×11,and the initial weightsWlare zero,wherel=1,3.The input vector of the RBF NNs is designed asZ=[u,v,r]T.The control gains are chosen asK1=2 ,K3=10,κ1=0.003,κ3=0.5, α1=5, α3=5,µu=20,µr=20,β1(0)=0,β3(0)=0.

For training the PFACN,random constant speed is chosen for each episode to learn from different dynamic scenarios.We train a model on the source task with the reward parameters λx=1,λy=1,first,then we adjust the reward parameters to λx=0.5,λy=1.5,=0.02,and other conditions remain the same.We transfer the whole network parameters and continue training model.For comparison,we choose a standard line-of-sight (LOS) guidance law [2] with look-ahead distance δ=5,and a pure pursuit and LOS guidance law(PLOS) [15] withk1=0.9,k2=0.18.Fig.3(a) shows the DDPG approach achieves less overshoot and reaches steady-state faster.After 25 s,the root mean squared error (RMSE) values of cross tracking are shown in Table 1,which indicates that DDPG also performs better in RMSE.Another illustration is in Fig.3(b).Due to the rewardDDPG quickly moves towards the endpoint,which is similar to PLOS.The low scores of LOS inalso lead to the low reward value in Table 1.Note that tuning control parameters may affect the results of LOS guidance,these tasks still validate the performance of the DRL-based approach.From Fig.3(c),the heading error of DDPG converges to a small neighborhood of the origin.The norms of NN weights are bounded as shown in Fig.3(d).

Table 1.RMSE and Reward

By equipping with the learned PFACN,the leader and Follower1 are chosen to train the FACN.Fig.4(a) shows the desired relative angle is achieved,then in this case no communication is needed.However,the action in Fig.4(b) is very aggressive even with the penalty term inrF.Instead of tuning the reward function,we propose a potential function ζu(motivated by [16]) to smooth the action

Fig.3.Tracking performance of the straight path following task.

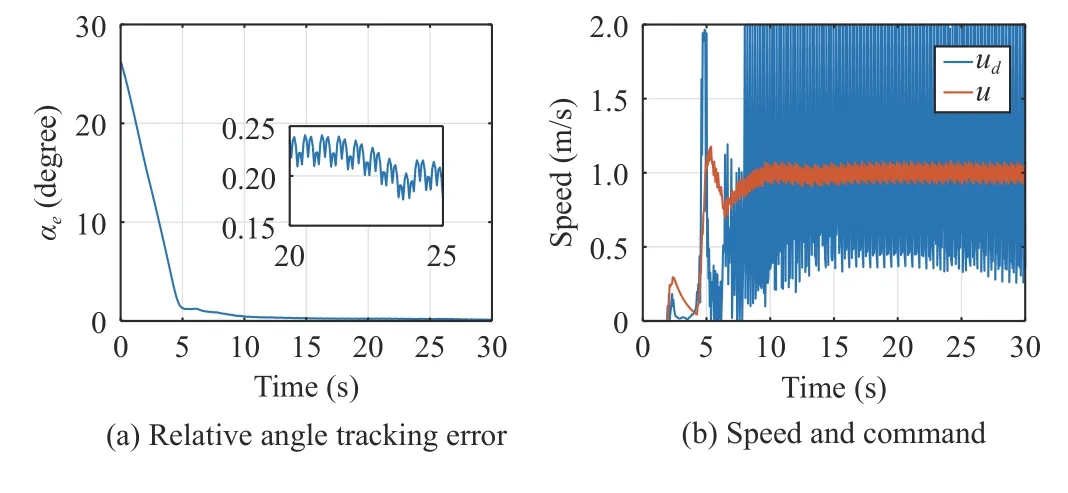
Fig.4.Evaluation of the FACN performance.

Fig.5.Evaluation of PFACN and FACN with the potential function.

Conclusion:This letter has investigated the problems of USV path following and formation control.Based on a distributed DRL method,a PFACN and a FACN have been formulated to achieve accurate guidance and adaptive formation control.The input saturation problem,the unknown disturbances and model uncertainties are addressed by an NN-based controller.Finally,numerical examples have been carried out to demonstrate the effectiveness of the proposed method.

Acknowledgments:This work was supported by the National Natural Science Foundation of China (U2141238).