Prescribed-Time Stabilization of Singularly Perturbed Systems

Yan Lei,Yan-Wu Wang,Xiao-Kang Liu,and Wu Yang

Dear Editor,

This letter investigates the prescribed-time stabilization of linear singularly perturbed systems.Due to the numerical issues caused by the small perturbation parameter,the off-the-shelf control design techniques for the prescribed-time stabilization of regular linear systems are typically not suitable here.To solve the problem,the decoupling transformation techniques for time-varying singularly perturbed systems are combined with linear time-varying high gain feedback design techniques.A composite linear time-varying state feedback controller is designed,and the existence of the time-varying Chang transformation matrix for decoupling the slow and fast dynamics is guaranteed.As a result,the prescribed-time stability is ensured.Finally,a numerical example is provided to illustrate the effectiveness of the results.

Recently,the finite-time stabilization problem has attracted a lot of attention in control community due to its wide applications [1]–[3],such as spacecrafts,mobile robots and underwater vehicles.Noted that,by finite-time stabilization,the settling-time would grow to infinity when initial state grows to infinity.Thus,the fixed-time stabilization problem was further studied,where the settling time is uniformly bounded and independent of the initial condition.Many mature effective tools such as homogeneous approach [4] and [5],implicit Lyapunov function approach [6] and [7] and Lyapunov based approach [8] and [9],have been developed for analysing the finite-time and fixed-time stability.Furthermore,considering the problem that the true settling time is predefined exactly,the prescribed-time stabilization problem was investigated,where the time varying high-gain feedback approaches have been developed as an effective tool for achieving the prescribed-time stabilization of linear systems [10] and nonlinear systems [11] and [12].However,all these works on prescribed-time control design focus on single-time-scale systems.

In practical,dynamic systems exhibiting two-time-scale feature appear in many applications [13]–[15],e.g.,electrical circuits,power systems and robot systems,and can commonly be modeled as singularly perturbed systems,where the small positive parameter multiplying the derivative of the fast state can be used to describe the timescale separation between slow and fast dynamics.Many valuable results on the asymptotic or exponential stability of singularly perturbed systems have emerged [16]–[18].However,as far as we know,the results on the finite-time stability of singularly perturbed systems are still limited.In [19],the fixed-time stabilization is achieved for linear singularly perturbed systems with assuming that the control matrix is of full row rank.It is worth noting that,although the expected settling time can be adjusted by suitably choosing the control parameters in [19],the true settling time can not be predefined exactly due to the conservatism of the theory.

In this letter,the prescribed-time stabilization of linear singularly perturbed systems is investigated by linear time-varying feedback.Due to the numerical issue caused by the small positive parameter,the techniques for the prescribed-time stabilization of single time scale systems are not applicable here.To handle the above problem,the decoupling transformation techniques for time-varying singularly perturbed system are combined with linear time-varying feedback design techniques.It is noted that,to ensure the prescribed-time stability,the time-varying control gain would commonly go to infinity in finite time,which would bring the difficulty of decoupling the singularly perturbed systems into slow and fast dynamics.Especially,the standard model reduction techniques cannot be directly resorted here.To handle it,a time-varying Chang transformation matrix is introduced,where the existence of such matrix is guaranteed.Correspondingly,a composite linear time-varying state feedback controller is design and the prescribed-time stability is ensured.The main contributions of this letter is twofold.

1) The prescribed-time stabilization problem is handled for singularly perturbed systems.Compared with [19],a more general linear singularly perturbed system is considered where the control matrix is not required to be full row rank,and the true convergence time can be predefined exactly regardless of the initial condition.

2) The time-varying Chang transformation is introduced to separate the linear singularly perturbed systems with linear time-varying high gain feedback controller into slow and fast dynamics.Moreover,the existence of such transformation matrix is guaranteed.

Problem formulation:Consider the following singularly perturbed system:

The objective is to design a linear time-varying controller

such that the origin of the closed-loop system(1) and (2) isT-global finite-time stable whereT>0 is user-defined,as formalized next.

Problem1: GivenT>0,design a bounded controller (2),so that the origin of system(1) and (2) isT-global prescribed-time stable.

Noted that,the true settling time can be arbitrarily and exactly predefined regardless of the initial condition here,which is different from finite/fixed-time stability.To solve Problem1,the next standards assumptions and one lemma are introduced.

Assumption 1: The matrixA22is invertible.

Assumption 1 and 2 are standard and commonly used in the singularly perturbed literature [13] and [14].

Lemma 1 [10]: Suppose Assumption 2 holds.Consider the parametric Lyapunov equations (PLEs)

1) The PLEs (3) and (4) both have unique solutions if and only if

2) Suppose (5) is satisfied and denote πs( γ)=2tr(A0)+nxγ,πf( γ)=2tr(A22)+nfγ .Then,there exist constants δsand δf,which are independent ofγ,such that

Main results:In this section,the prescribed-time control of system(1) is studied.

Block-diagonal model: Firstly,we introduce the time-varying Chang transformation to separate the slow dynamics from the fast ones,which is given by

where Λij(t)=Ai j+BiK j(t),i,j=1,2.It is noted that the existence of the matricesL(t) andH(t) satisfying (10) will be ensured,and the details can be seen in the proof of Theorem1.

Remark 1: Noted that the decoupling transformation technique for linear time-varying systems in [13] is only applied when the system matrix is continuously differentiable and bounded.However,to achieve the prescribed-time stability,the control gain would commonly go to infinity in finite time.The existence of such matricesLandHshould be re-discussed,which is one of the challenges here.

With state transformation (9),It has

Thus,the origin of system(1) and (2) isT-global finite-time stable.Similarly,it has∥limt→T∥u∥=0.The control signal will not go to infinity with bounded initial states.

Remark 2: From Theorem1,the matricesH(t) andL(t) are not bounded fort∈[0,T).The prescribed-time stabilization of system(11) can not be directly equivalent to solving problem1.Thus,(19) is further proved to guarantee the prescribed-time stability property.

Remark 3: Different from [19],the prescribed-time stabilization problem is considered,where the true settling time can be predefined exactly regardless of the initial condition.Beside,benefiting from linear time-varying feedback design,the additional assumptions that the control matrix is full row rank can be removed.It is also worth noting that numerical problem caused by γ(t) has been discussed in Remark 1 of [12] and an effective method has been established to overcome it,thus corresponding discussion is omitted here.

Illustrative example:Consider the singularly perturbed system(1)with ε=0.1 and

The simulation results with different initial conditions are presented in Figs.1 and 2,which show that the origin of the system isTglobal prescribed-time stable,and the control signal is bounded,regardless of the initial condition.

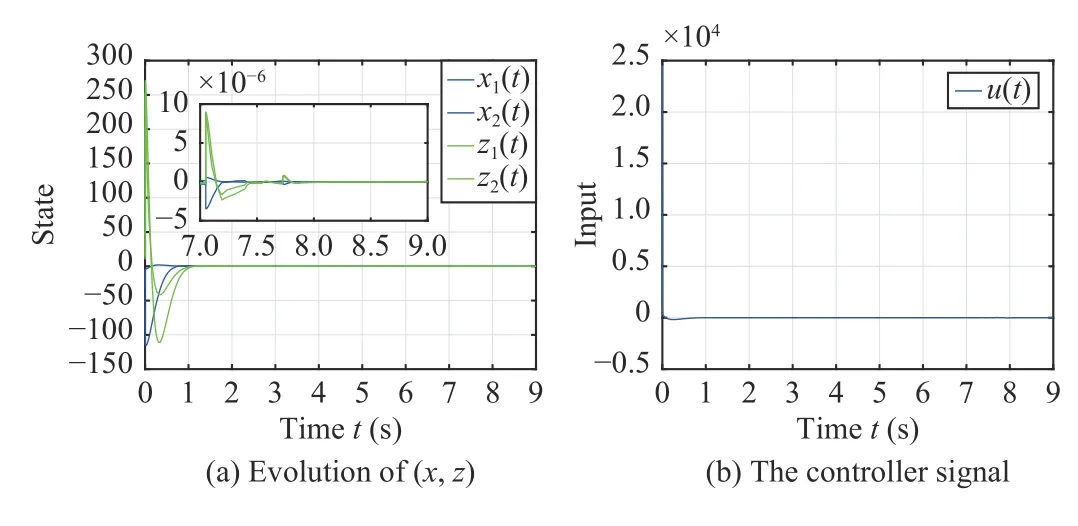
Fig.1.The simulation results with small initial state value.

Fig.2.The simulation results with large initial value.

Conclusion:In this letter,the prescribed-time stabilization problem is investigated for linear singularly perturbed systems.By combining the decoupling transformation techniques and linear time varying high gain feed back design techniques,a composite linear time-varying state feedback controller is designed,so that the prescribed-time stability is ensured.It would be interesting to further consider output feedback control and address cyber attacks.

Acknowledgments:This work was supported by the National Natural Science Foundation of China (62173152,62103156,62233006),the Natural Science Foundation of Hubei Province of China(2021CFB052),and the China Postdoctoral Science Foundation(2022M 721249).