单通道涡流无损检测信号盲源分离算法
2023-03-08杨智伟南新元
杨智伟, 南新元
(新疆大学 电气工程学院,新疆 乌鲁木齐 830047)
新疆油气资源丰富,随着“西气东输”工程的推进,疆内已铺设完成压力管道超8 200 km。面对现场的复杂工况、恶劣天气以及管道中液滴冲击等不可抗因素,管壁局部缺陷时有发生。为保障压力管道安全可靠地运行,避免事故发生,定期对管道进行无损检测尤为重要。
由于压力管道管壁较厚,传统的涡流无损检测被趋肤效应影响,检测深度受限。脉冲涡流无损检测(pulsed eddy current testing,PECT)相较于传统的涡流无损检测,具有丰富的频谱信息且可检测深度较大,因此被广泛应用于压力管道无损检测中[1-2]。
由于铺设场地工况复杂,PECT隶属于电子系统,除去噪声还存在一定的高频干扰等[3],可将缺陷信号从干扰源和缺陷信号混叠中分离的过程视作盲信号分离问题[4]。针对此问题,文献[5]提出了一种解决盲信号分离问题的独立分量分析(independent component analysis,ICA)算法,较好地完成了分离工作;文献[6]在此基础上改进了迭代公式,并提出了FastICA算法,极大地提高了收敛速度。传统的ICA算法要求观察信号通道不低于源信号数,才能获得更好的分离效果[7]。然而PECT常采用单一检测线圈探测混叠场电压信号或是单一霍尔传感器对磁通密度进行检测,采集到的检测信号是单通道的混合信号。在此前提下,需要将单通道混合检测信号拓展为若干个虚拟观测信号。传统的小波变换可以对单通道信号做分解,但分解层数与小波基的选取会影响分离效果[8]。文献[9]针对非线性复杂信号的分解,提出了经验模态分解(empirical mode decomposition,EMD)算法,可将混合信号按频率分解为固有模态函数(intrinsic mode function, IMF)分量。基于上述论述,本文提出了一种EMD-FastICA算法的PECT,将原始混合信号分解为各模态分量,经判定选取模态分量及模拟检测信号组合继续通过ICA解混去噪,由先验条件可判定提取初始信号。
1 理论基础及算法原理
1.1 PECT基本原理
PECT原理示意图如图1所示,在激励线圈中通入一定占空比的脉冲激励电流。
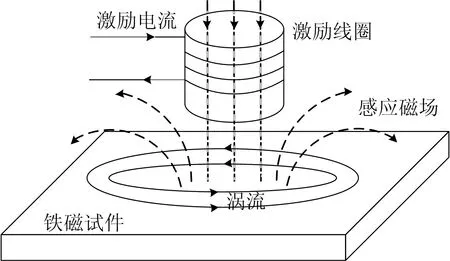
图1 PECT原理示意图
依据电磁感应定律在激励线圈靠近金属试件时,产生的激励磁场会在试件中感应出同频涡流,涡流衰减产生感应磁场叠加激励磁场形成一个复合场。而此叠加场受到试件缺陷处电磁特征不连续性的影响会产生变化,通过对此信号分析可以判断试件的缺陷特征[10]。
1.2 FastICA算法
盲信号分离原理如图2所示,设s(t)=[s1(t)s2(t) …sN(t)]T为N个相互独立的源信号,经未知M×N维矩阵A线性混合得到x(t)=[x1(t)x2(t) …xM(t)]T。

图2 盲信号分离原理
盲信号分离是通过优化算法寻求一个分离矩阵W,再利用分离矩阵W对观测信号x(t)解混得到信源s(t)的估计y(t)。
由于多个相互独立的随机变量之和趋于高斯分布,当分离信号的非高斯性最大时,可以判定分离完成。基于此原理采用FastICA算法,用最大熵原理近似负熵的方法度量随机变量的非高斯性[11],其近似公式可表达为:
J(Y)=[E(G(Y))-E(G(YGauss))]2
(1)
由FastICA原理和前提条件可将迭代式转化为:
(2)
其中,z为白化处理后的数据。
FastICA算法实现流程如下:
(1)为去除矩阵的相关性,计算白化矩阵H,使得z=Hx白化。
(2)对于当前提取的第i个信号,任取ui(0),使其满足‖ui(0)‖=1。根据迭代(2)式计算ui(k+1)。
(3)正交并归一化ui(k+1),继续判断ui(k+1)收敛性,若未收敛,则返回步骤(2)。
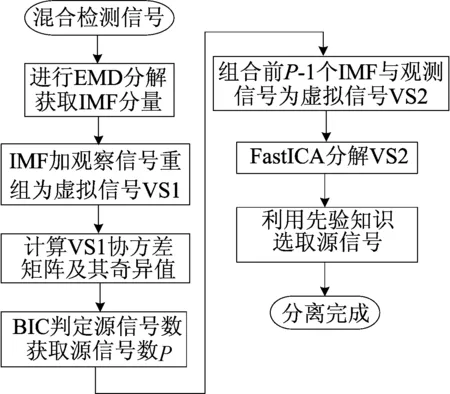
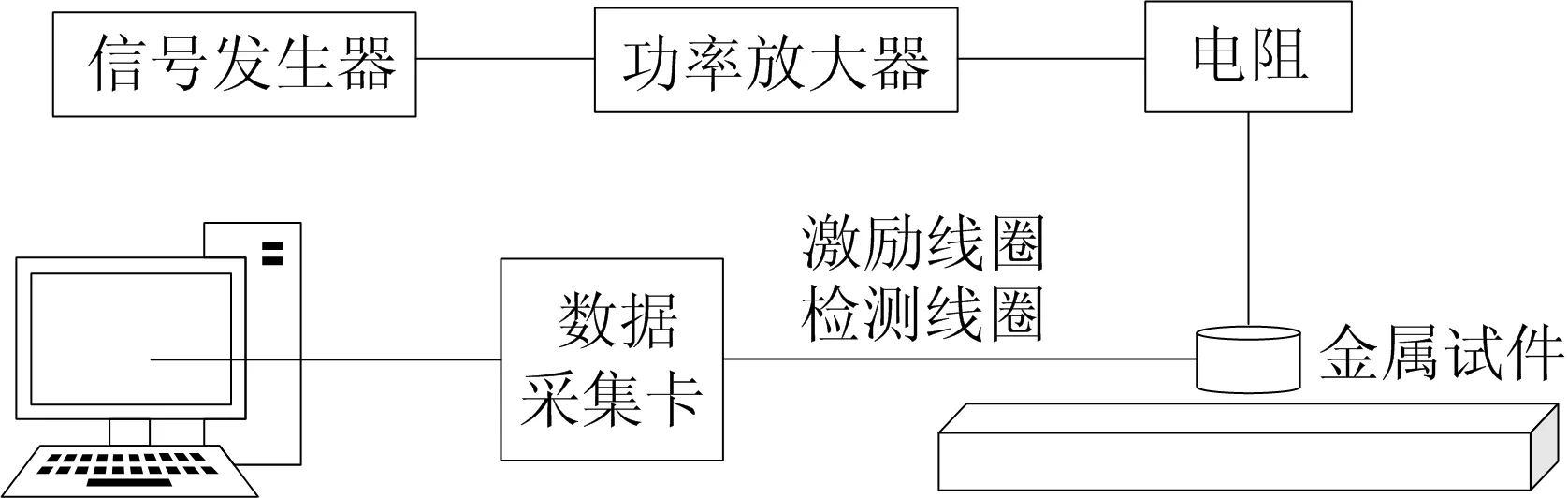
(4)设源信号数目为m个,i=i+1,若i EMD算法依据信号自身时频特征进行分解,相比傅里叶或小波分解,不需要预设基函数,在处理非平稳非线性的涡流检测信号时具有明显优势。EMD算法可以自适应地将信号由多频率的混合信号分解为若干个单一频率,并且从小到大排列IMF分量和一个残余信号。 (3) 其中:c为包含源信号自身频率特征的本征模函数以及包含噪声的本征模函数;r为残余信号。经由EMD分解,可以将单通道的检测信号拓展为多通道虚拟信号。具体步骤[12]如下。 (1)将混合检测信号通过三次条样函数对混叠信号极大值与极小值分别拟合,组成上下包络线e1(t)和e2(t),求取包络均值得: (4) (2)将混合观测信号x(t)减去包络均值m1(t)得到差值g1(t),进一步将g1(t)视作待处理信号重复步骤(1)多次,得到: gi(t)=gi-1(t)-mi(t) (5) (3)直到gi(t)符合本征模函数的特征,其中i≥1,记: f1(t)=g1(t) (6) (4)将混合检测信号减去上述第1个本征模函数,得出x1(t);将其看作初始信号继续重复步骤(1)~步骤(2)。一次提取出m-1个模态函数f(t),同时将不包含任何模态信息的单调信号视作残余函数,即rn-xm-1(t)。 在实际运算中,本征模态函数作为判断条件需要满足极大点和极小点构成的上下包络均值为0和极大点、极小点差值最多为1的条件。 检测信号经由EMD 分解后得到若干组囊括源信号全部信息的IMF分量,然后利用FastICA算法即可对源信号分离还原,但源信号的维数通常不可知,此时需要通过算法对源数目进行估计。文献[13]提出了一种基于奇异值分解(singular value decomposition,SVD)的贝叶斯信息准则(Bayesian information criterion,BIC)(SVD-BIC)源数估计法,首先通过计算IMF分量的协方差矩阵,然后结合BIC,计算判定。 (7) 对于求取检测信号中源信号数目的估计,BIC的方法寻找一个使BIC(k)取最大时k值的序号。 为实现在强干扰及噪声下对原始采集信号的提取,结合上述经验模态分解以及独立成分分析2种算法优势,提出了一种经由EMD和FastICA联合的特征提取算法[14]。综合本文提出的算法,具体实现步骤如下。 (1)将混合检测信号经由EMD分解得到若干组IMF分量。 (2)将检测信号和得到的IMF分量组合为虚拟信号VS1,并计算协方差矩阵,按照降序的排列获取其奇异值向量τ。 (3)计算BIC(k),当其值最大时记k值序号为P,得到源信号估计数目为P。 (4)取前P-1组分量和检测信号构成P维虚拟信号VS2。 (5)把上述虚拟信号VS2通过FastICA继续分解得到P维分离信号,对P个分离信号做频域分析。 (6)由激励线圈频率的先验知识,分析经ICA处理获得的分离信号可判别实际检测信号。 算法流程如图3所示。 图3 算法流程 COMSOL是一款有限元仿真软件,该软件可以实现多物理场的耦合计算。本文主要调用其中磁场和电路2个接口,通过对压力管道、激励线圈、检测线圈以及空气域等模型的构建,给定激励信号计算出复合场施加在检测线圈两端的电压等数据。 基于屈服强度为485~605 MPa的X70管道的结构参数,设定仿真模型为内径550 mm、外径650 mm的压力管道,同时在管壁内侧中央位置设置一矩形缺陷,宽度为2 mm,长度为10 mm,深度为7 mm。线圈放置于管壁外侧正对缺陷位置,其直径为20 mm,提离距离为5 mm,匝数为298匝。由于仅研究干扰对脉冲涡流检测信号的影响,将模型简化为二维模型以提升计算效率。建立的二维模型如图4所示。 在实际脉冲涡流无损检测系统中,通过信号发生器外加功放获得足够强度的电流去驱动探头,在COMSOL软件中可以通过外加电路物理场来激励线圈输入电流。 PECT系统原理图如图5所示。从图5可以看出,该脉冲涡流无损检测系统中利用检测探头探测缺陷信号,通过检测线圈接入数据采集卡并连接上位机可获取检测电信号[15]。 图5 PECT系统 在本文仿真模型中,模拟实际检测系统于激励线圈正下方处放置一检测线圈,设置其匝数为300匝,在电路端外接电压表采集电压数据,设置方波脉冲的频率为10 Hz、占空比为50%、工作电压10 V的激励信号。采集此激励下的检测信号如图6所示。 图6 理想条件下检测线圈的电压信号 为模拟强干扰信号对检测信号带来的影响,给定幅值、频率和相位均不相等的正、余弦信号各一个混入检测信号,且作为强干扰幅值大于原始信号。同时在混合信号中加入随机噪声模拟实际情况下的检测信号。给定信号为s1、s2: s1=15sin(2π×50t) (8) s2=17cos(2π×27t+π/3) (9) 检测信号视为s3,记S=[s1s2s3]T,然后将上述信号通过一组3×3维的随机矩阵A进行混合,用以模拟原始信号和干扰信号在未知信道线性混合的过程。 上述信号经混叠后得到3个混合信号,随机选取混合信号中的一组信号作为单通道检测信号,其时频图如图7所示。 图7 检测信号时频图 从图7可以看出,原始信号几乎淹没在干扰中,频域信息已不明显。 对检测信号进行EMD分解,IMF分量如图8所示。 图8 模拟观察信号经EMD分解结果 从图8可以看出已经分解得到的IMF分量信息大多集中在前3组。运用SVD-BIC算法,将分解所得IMF模态分量与模拟检测信号重新组合得到虚拟信号VS1,通过求取协方差矩阵以及对应奇异值求出VS1对应的k个BIC值,绘制点线图如图9所示。 图9 虚拟信号对应的BIC值 由图9可知,当k=3时BIC值最大,因此可知源信号数为3,这与观察和预设一致,说明经过此方法估计源信号数目具有可行性。进一步将前2组IMF分量与检测信号组合为另一组虚拟信号VS2。将虚拟信号通过FastICA再次处理可以得出经由混合的3组源信号。同时将分离经由FastICA分离出来的3组信号做小波软阈值去噪,分离所得3组信号时频图如图10所示。 图10 FastICA分离时频域图 由于输入激励信号频率为10 Hz,检测信号为激励信号感生而来,因而得出的检测信号频率应当也为10 Hz左右。观察分离得出3组信号的频谱图,分离得出的第3组信号频率约为10 Hz,这与先验条件相符,且观察时域波形图也符合在脉冲涡流激励信号作用下的检测信号。可以判定第3组分离信号为实际缺陷检测信号。 由于经过FastICA计算后3组原始信号的幅值会发生变化,可以用相似系数[16]来分析对源信号的提取效果。相似系数εi定义为: (10) 其中:s(n)为理想条件下得到的检测信号;x(n)为分离信号。代入计算结果见表1所列。 表1 算法性能对比 通常认为相似系数越接近于1的2个信号越相似,反映出的分离性能越好。依据表1计算结果可知,本文算法较好地提取出微弱检测信号,并完成对混叠信号的解混去噪。由于文献[17]在选择小波包节点时,依据节点的能量系数比为: (11) 其中:En为小波包分解得到的第n个节点能量值;E为总能量值。 对于幅值相对较小的检测信号,其占比较小致使分离效果不佳。因此,针对较强干扰下的检测信号,其盲分离效果优于文献[17]提出的算法。 本文针对在较强未知干扰和噪声条件下的压力管道脉冲涡流无损检测源信号提取困难的问题,提出了一种基于EMD-FastICA的信号分解重构提取算法。通过仿真模型模拟检测信号的构建与对源信号的提取验证,表明本文提出的算法能有效地分离出较强干扰下的微弱脉冲涡流检测信号,结果较好地反映了源信号的时频特征,可以满足工程实际要求。1.3 EMD算法
1.4 复合算法流程
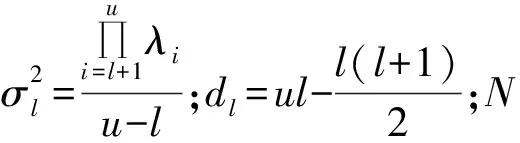
2 有限元仿真模型的建立
3 信号的获取与处理
3.1 仿真信号的获取
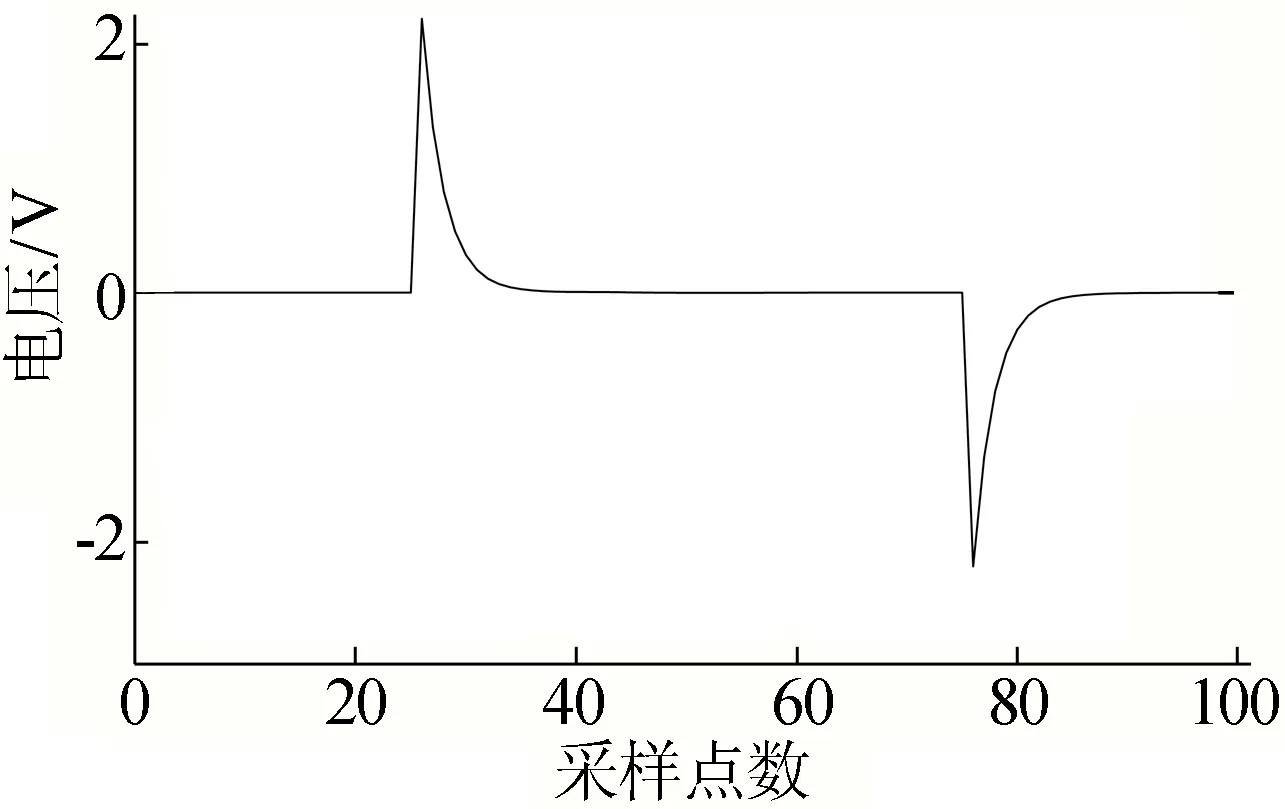
3.2 模拟观测信号的获取


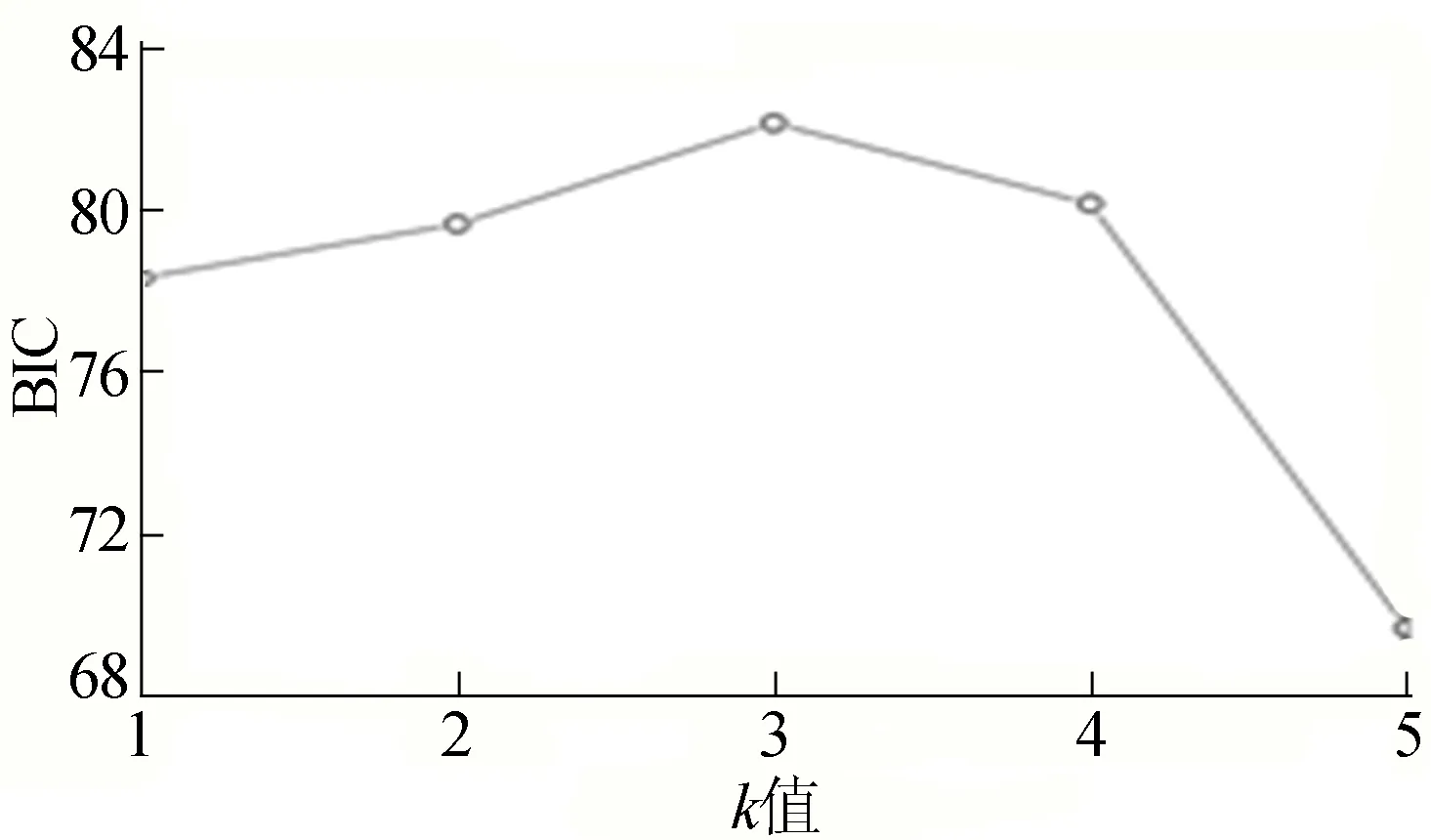
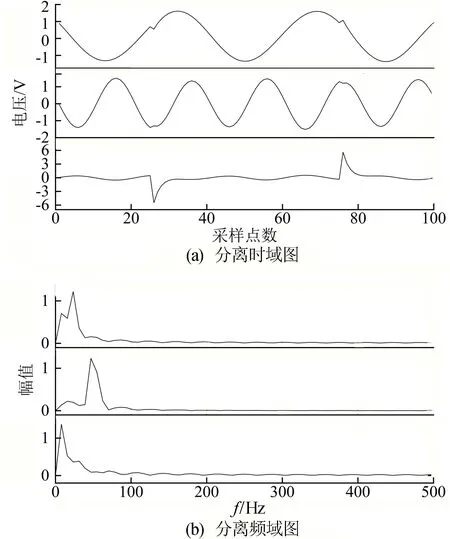
3.3 算法分离结果及分析

4 结 论
