考虑风载作用的绝缘穿刺线夹多物理场耦合研究

2023-03-08吴少雷汪张宝何文信

合肥工业大学学报（自然科学版） 2023年2期

冯玉, 吴少雷, 吴凯, 汪张宝, 何文信, 王伟

(1.国网安徽省电力有限公司电力科学研究院,安徽合肥 230601; 2.合肥工业大学机械工程学院,安徽合肥 230009)

0 引言

随着经济的快速发展,用电需求的不断增加给电力传输带来严峻的挑战。高压架空线路是电力传输的核心,需要大量使用接续金具实现电能分流,为城市、农村和企业等提供电能。接续金具因具有操作便捷、对导线的损伤小、可以带电作业等优势,在导线接续工作中得到广泛应用。然而,在实际服役中,大量分布的接续金具会出现性能退化,导致供电线路故障甚至引发严重的火灾[1]。相关研究表明,在多场耦合工况下,接续金具的接触电阻增大或大载流等会产生显著温升,进一步恶化金具的服役性能,最终导致架空线路故障[2-3]。因此,有必要对接续金具的多场耦合特性展开相关的研究。

有限元法(finite element method,FEM)是接续金具多场耦合分析常用的方法。但众多的分析是基于电接触的静态理想工况建立相应的耦合模型,文献[4-5]采用有限元仿真分析电连接器在室温、静态下的温度分布特性,并结合温度场结果分析了电连接器的结构特性;文献[6]在绝热环境下考虑接触表面状态对接触电阻和生热的影响,并进行了温度场与结构场的耦合演变分析;文献[7]研究了绝热工况下电源连接器的热行为,对热结构耦合失效机理进行深层次的分析。研究表明电接触会产生明显的生热现象,使得电连接器承受较大的热负荷,而生热量取决于多方面的影响因素;文献[8]建立了多尺度粗糙表面的多场耦合电接触模型,并结合该模型分析接触材料属性、表面粗糙度等对电连接器的生热影响,进一步分析某温度下电接触性能与可靠性;文献[9]建立大电流电接触的热电耦合模型,研究了电流脉冲和短路工况下触点的瞬态温升,并分析了瞬态热效应对接触电阻的影响。因此,材料属性、表面接触状况及通电电流等对温升具有较大的影响,导致电连接器在不同的服役条件下温升也有较大的差别,尤其是在大电流及静态理想条件下,连接器温升更加显著。

众多研究表明电连接器的失效主要与温度有关。文献[10-11]针对GIS梅花接头的过早失效展开研究,建立该接头的多场耦合模型,研究发现接头插入深度不足时接头过热,发生过热性故障,并进行接头的温升实验,验证该计算模型的有效性;文献[12]基于ANSYS分析导线直径对汽车电连接器电接触性能的影响,研究结果表明适合的导线直径能够降低连接器的温升,高温使得连接器发生粘接而失效;文献[13]建立了AgNi10触头的热电力耦合模型,并考虑温度对材料特性的影响,发现电流密度在接触区域呈环形分布,形成环形热源,造成接触区域热应力集中,易于形成裂纹源,最后断裂失效。综上所述,多场耦合下电连接器的电接触性能及寿命受到多方面因素的影响,其中温度是重要的影响因素,温度过高会进一步恶化电接触性能,最终导致连接器烧蚀或断裂失效。风载作用可以缓解连接器相对高温带来的不利影响,但也会让连接器承受较大的循环应力,尤其是穿刺线夹的风载作用更加剧烈。

为研究风载作用时穿刺线夹的温度分布及结构应力,本文建立穿刺线夹电热力多场耦合模型,并完成穿刺线夹在不同安装扭矩下接触电阻的测量实验,将通电下的接触电阻热换算成生热量施加到有限元模型中,考虑风载作用对穿刺线夹散热及结构应力波动的影响,定义合理的热对流边界条件和循环振动载荷,得到线夹在不同安装扭矩下的温度场及结构场特性,分析安装扭矩对线夹温升、应力分布等的影响,为线夹更好的服役提供理论依据。

1 分析基础理论

1.1 接触电阻理论

金属材料的加工表面并非理论上的光滑表面,而是存在无数个微小粗糙峰,同时存在氧化膜及其他污染膜。当2个金属表面在一定的压力作用下相互接触时,微观粗糙峰会刺破接触表面的绝缘膜层,从而形成无数微小的接触斑点(称为α斑点),这些斑点是电流导通的唯一路径[14]。当电流通过接触表面时,由于α斑点的离散分布,电流线会产生收缩,形成收缩电阻,与膜层电阻共同构成接触电阻,穿刺线夹-导线的接触电阻示意图如图1所示。

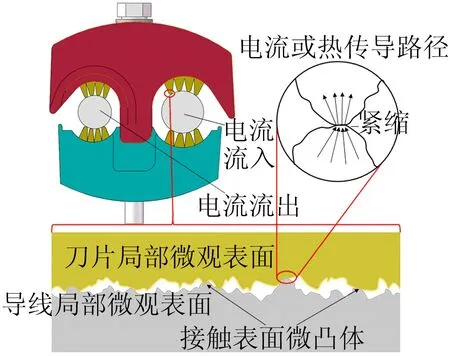
图1 穿刺线夹-导线接触电阻示意图

1.2 穿刺线夹受力分析

绝缘穿刺线夹(以下简称线夹)通过线夹上的2个定扭矩螺栓安装在导线上，螺栓拧紧过程中，由于螺栓与被连接件表面粗糙不平，各部件之间会存在摩擦作用。螺栓安装示意图如图2所示。

图2 螺栓安装示意图

安装时扭矩需要克服螺纹接触面间摩擦力矩Mk以及螺母与被连接件间的摩擦力矩Mg，余下扭矩Mr转化为螺栓的预紧力。相关计算表明，螺栓拧紧过程中大约50%的扭矩用于克服有关部件之间的摩擦力，大约40%的扭矩用于克服螺纹副之间的摩擦力，真正转化为螺栓预紧力的部分大约为10%。

拧紧过程中所需的安装扭矩计算公式为:

M=Mr+Mk+Mg=

(1)

其中:F0为螺栓预紧力;P为螺距;μk、μg分别为螺纹连接面间和螺母压面处摩擦系数;d2为螺纹中径;Dkm为中心直径。

本文研究的线夹型号为JJC 10-240/150,采用M8紧固螺栓,该螺栓相关参数见表1所列。

表1 螺栓相关参数

考虑到线夹在安装过程中会对导线产生较大的接触压力,该穿刺线夹允许施加的最大安装扭矩为32 N·m,于是取14～32 N·m的范围,并以2 N·m作为梯度选取数据进行计算,螺栓在每一级安装扭矩下对应的预紧力见表2所列。

表2 线夹螺栓预紧力

1.3 接触电阻等效处理

接触电阻是线夹工作时热量的主要来源,对接触电阻进行准确的等效处理是线夹多场耦合分析的关键。因为接触电阻是接触表面的粗糙不平造成的,接触电阻产生的热量也集中在两导体接触表面处,所以在电-热耦合仿真的过程中可以通过接触面的产热量来进行模拟[15]。

对于线夹-导线模型来说,因为接触电阻只存在于穿刺刀片与导线的接触部位,所以接触电阻造成的功率损耗仅存在于穿刺刀片两端的接触面上,因此穿刺刀片金属触头处接触电阻的生热率q计算公式为:

(2)

其中:i为电流;Rc为总的接触电阻;S为所有触头的接触面积总和。

接触电阻数值与安装扭矩的关系如图3所示。通过实验测量线夹-导线在不同安装扭矩及激励电流下的接触电阻,结合(2)式计算载流量为290 A时不同安装扭矩下接触电阻的生热率，即可得到表2中的数据。

图3 接触电阻与安装扭矩的关系

2 仿真模型建立

2.1 模型简化与前处理

在建立线夹的有限元模型时,为减少模型规模,节约计算资源,避免复杂结构造成网格质量差使得计算结果难收敛的问题，本文对穿刺线夹模型进行如下简化。

(1)舍去线夹两绝缘外壳之间的配合凹槽、表面凹凸结构及细小的过度圆角等。

(2)去除螺栓上方定扭矩断裂部分,对线夹的螺栓、螺母上的螺纹进行简化。

(3)简化电缆导线,将与线夹配合的输电线简化为单一线径的圆柱导线。

将简化后的线夹3D模型导入ANSYS Workbench中,简化后的模型如图4所示。

图4 简化模型示意图

2.2 定义材料属性及网格划分

线夹结构中有多种材料类型,需要在模型中定义合理的材料属性参数。在电-热耦合分析中,需要使用的材料属性参数见表3所列。表3中,绝缘外壳及导线绝缘层的电阻率理论上无穷大,可以设置为9 999。热-结构耦合分析中所采用的材料属性参数见表4所列。

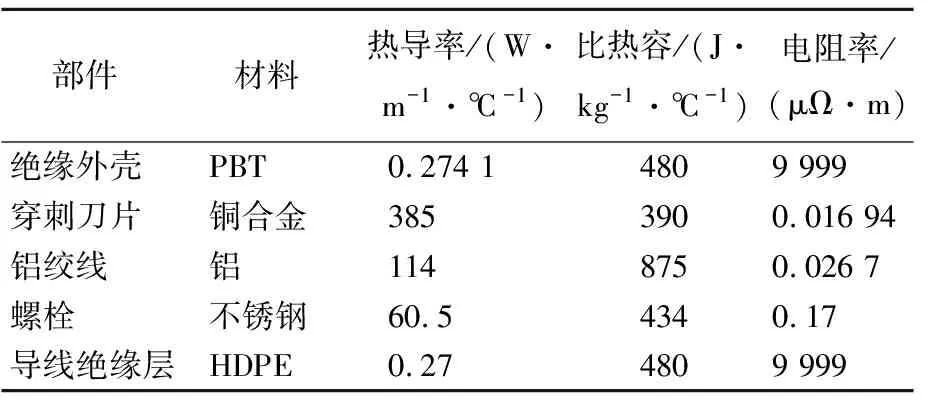
表3 线夹电-热耦合分析材料属性

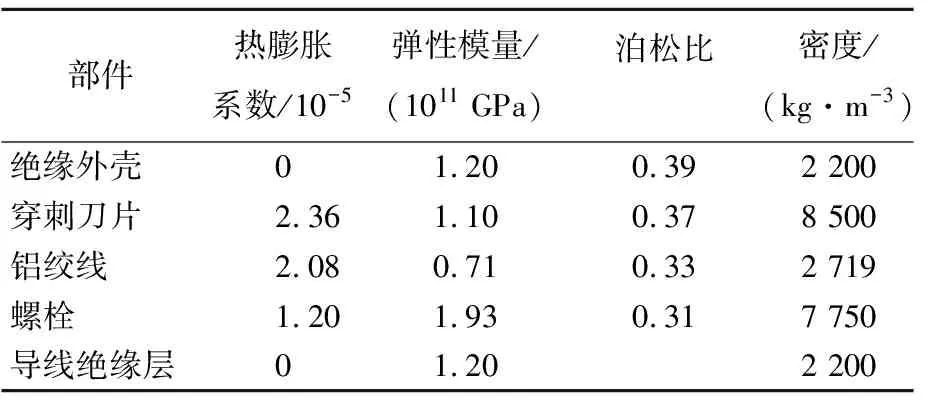
表4 线夹热-结构耦合分析材料属性

为保证仿真高精度的同时降低计算周期,对线夹-导线接触部位进行局部网格加密处理,采用六面体单元,整体网格尺寸设置为1.0 mm,其余没有接触部分的整体网格尺寸设置为3.0 mm,绝缘外壳设置为4.0 mm。导线外部的绝缘层根据其厚度,主导线绝缘层与支导线绝缘层网格大小分别设置为1.5、1.0 mm。网格划分后整个有限元模型中包含575 591个节点、184 285个单元,平均网格质量为0.804 39。

2.3 线夹边界条件

线夹多场耦合分析时,先进行电-热耦合稳态分析,再进行热-结构耦合瞬态分析。在电-热分析中,假设环境温度为30 ℃,考虑空气流速为5 m/s,对应工况下的线夹表面对流换热系数为5.78 W/(m2·℃),在主导线的端面施加290 A的稳定电流,在副导线的另一端面设置0的电压以模仿电流的导通。最后在穿刺触头表面以热通量的形式施加接触电阻生热率,以模仿接触电阻生热现象。

线夹-导线的电-热耦合稳态分析边界条件如图5所示。

图5 电-热耦合稳态分析边界条件

在电-热耦合稳态分析的基础上,将温度场仿真结果导入热-结构耦合瞬态分析中,作为初始载荷条件。此外,线夹还承受其他外载荷,如螺栓预紧力、自重、架空导线张拉力、风载荷等。根据文献[16]可知，该导线张拉力约为6 935.8 N,导线的风载作用根据卡门涡街及输电导线的风载理论振幅计算得到,并以循环位移载荷的形式施加在导线的一侧。基于瞬态动力学仿真分析法可以设置2个载荷步,设定第1个载荷步模拟穿刺线夹的安装过程,即对螺栓施加24 N·m的预紧力,为第2个载荷步分析提供预接触。其总时长约占总分析时长的1/10,初始分析子步数为10、最小子步数为1、最大子步数为20;第2个载荷步总时长设置为20倍导线单次振动的周期,子步数为100。热-结构耦合瞬态分析边界条件如图6所示。

图6 热-结构耦合瞬态分析边界条件

3 仿真结果分析

3.1 温度场结果分析

线夹电-热耦合稳态分析的最终温度分布如图7所示。

图7 线夹温度分布云图

从图7可以看出,线夹整体温度分布呈现不均匀的状态。刀片的温度是整个线夹温度最高的区域,高达55.44 ℃,最低温度则出现在绝缘外壳两端及两绝缘外壳相互接触的部位,最低温度为35.14 ℃,温差为20.33 ℃。

从图7还可以看出,穿刺刀片的整体温度较为均匀,这是由于线夹内部处于封闭的状态,仅与绝缘外壳产生热交换,而绝缘外壳是由于低热传导率材料及刀片较高的热传导性能使得刀片维持在较高的温度；同时看出绝缘外壳与穿刺刀片接触的部分温度较高而绝缘外壳整体的温度较低,造成这种现象的原因在于绝缘外壳与空气存在对流热交换,并且绝缘外壳的导热性能较差,造成了内外的温差现象。这种内部温度集中现象不利于线夹的长期温度运行,会造成部件材料的受力不均易于老化失效。因此,绝缘外壳材料在保证高绝缘性、高强度的同时需要具备良好的导热性能。

线夹在不同安装扭矩作用下的最高温度、平均温度、最低温度变化如图8所示。

从图8可以看出,随着安装扭矩的增大,温度均呈现下降趋势,随后趋于平稳,这与接触电阻值随安装扭矩的变化趋势基本一致。在同样290 A载流量工况下,14、32 N·m安装扭矩下线夹的最高温度分别为49.03、86.42 ℃,温差达到37.39 ℃,可见安装扭矩对线夹温升特性具有重要的影响。文献[16]的研究表明，线夹在长期工作时允许的最高温度不应超过75 ℃,结合仿真结果可知,在额定载流量范围内,安装扭矩应大于18 N·m。

图8 不同安装扭矩作用下线夹温度曲线

3.2 结构场结果分析

由线夹热-结构耦合瞬态分析结果表明,可以得到在0.023 s时线夹-导线的应力分布云图，如图9所示。

由图9可知，线夹的最大应力位于穿刺刀片上,除去刀尖等应力集中区域,应力大小基本维持在350 MPa以内。

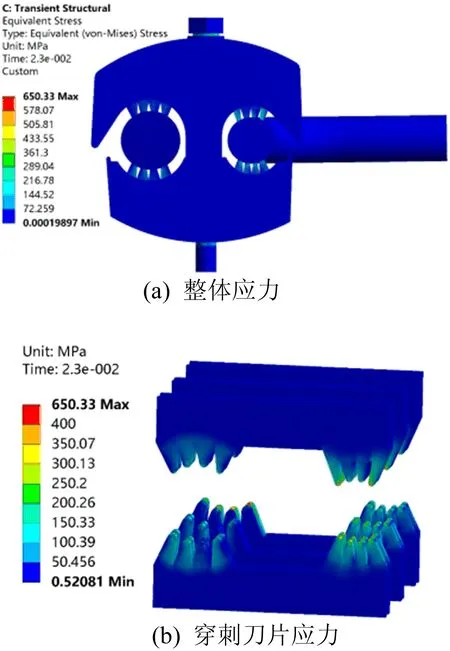
图9 线夹-导线的应力分布云图

线夹不同安装扭矩下的最大应力随时间的动态变化如图10所示。

由图10可知,线夹安装完毕后,大约0.03 s时线夹的最大应力达到最大,且随安装扭矩的增加而增大,在32 N·m安装扭矩时最大应力达到900 MPa,而后加入温度与风载振动载荷,线夹-导线的最大应力开始波动。当安装扭矩在24 N·m以下时,由于原始最大应力的差异使得最大应力围绕某一水平进行波动,但不同安装扭矩下的最大应力波动趋势基本一致;当安装扭矩在28 N·m以上时,各应力波动曲线大致在同一水平,仅有波动幅度的差异,安装扭矩越大总体上应力波动幅度越小,据此推测在大安装扭矩工况下,风载振动对线夹的最大应力波动影响越小。

图10 安装扭矩对线夹最大应力的影响

针对风载振动对线夹应力分布的影响,线夹风载振动导致最大应力波动幅度和最大应力增长量与安装扭矩的关系如图11所示。图11中,波动幅度为最大应力波动曲线峰值与谷值间的差,稳态均值为稳定波动时间段内通过曲线数据计算的平均值。

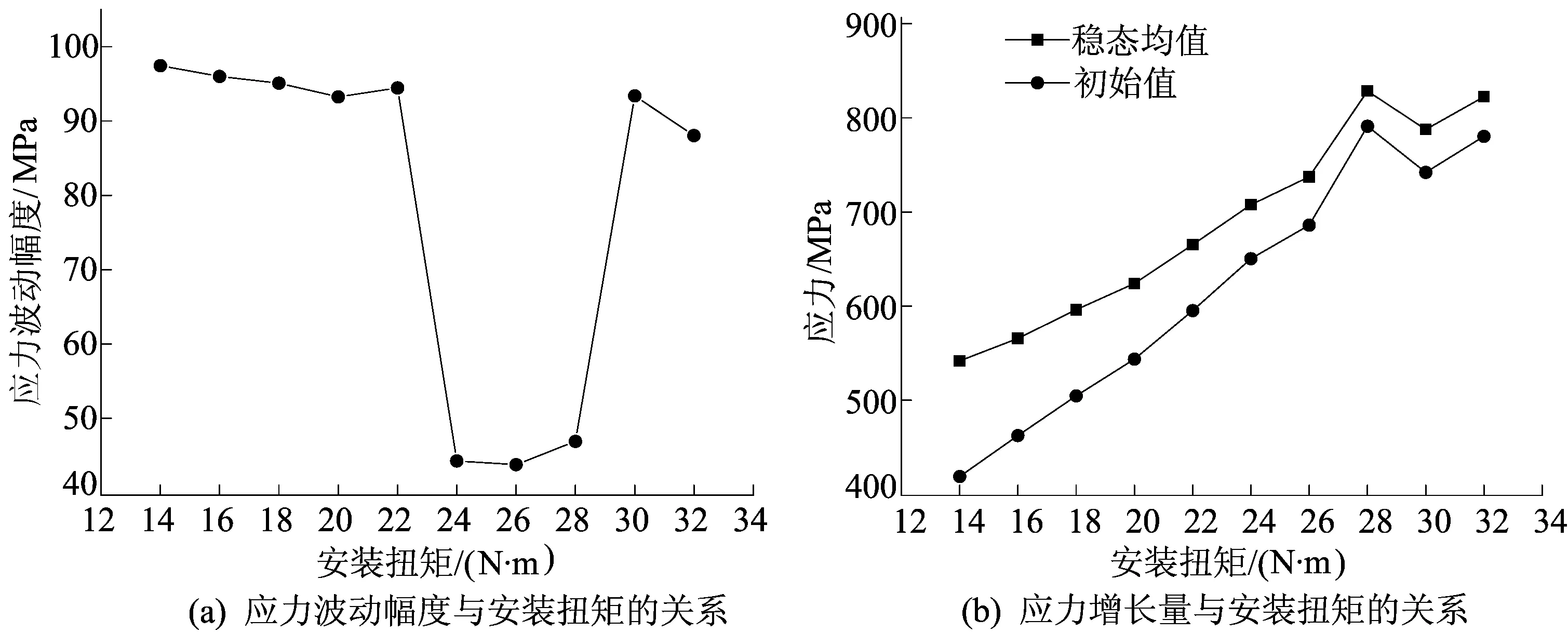
图11 安装扭矩对线夹最大应力波动特性影响

由图11a可知,随着安装扭矩的增加,线夹的最大应力波动幅度总体上变小,但局部存在明显的突变,造成这种现象的原因可能是由于改变安装扭矩导致接触电阻改变,使得多场耦合间的相互作用发生变化。当安装扭矩为24～28 N·m时,线夹的最大应力波动幅度明显降低,分别为44.25、43.75、46.89 MPa,可以认为在该安装扭矩范围内线夹的应力波动幅度受风载振动的影响较小。由图11b可知,随着安装扭矩的增加,稳态均值基本呈增长趋势,增长量也各不相同。当安装扭矩从26 N·m增加到28 N·m时,稳态均值增量最大,约为91.1 MPa,但较大的安装扭矩会大幅度地减小应力波动幅度,较小的应力波动幅度有利于延长线夹的疲劳寿命。综上所述,电-热耦合分析结果表明线夹适宜的安装扭矩范围为24～28 N·m。