基于电子齿轮箱非圆齿轮齿距误差补偿研究
2023-03-08郭振,夏链,韩江
郭 振, 夏 链, 韩 江
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.安徽省智能数控技术及装备工程实验室,安徽 合肥 230009)
非圆齿轮结合了一般齿轮和凸轮的优点,能够实现非匀速比传动,广泛应用于轻工业及仪器仪表行业[1]。齿轮在产生过程中,对多轴之间的联动有严格的要求[2]。传统齿轮加工依靠机械式的齿轮箱来保持各轴之间的传动比关系,因此齿轮的加工精度受到传动齿轮加工精度和安装精度的影响。
文献[3]根据滚齿机滚齿加工过程的理论模型,提出一种新的软件定义的滚齿机电子齿轮箱代替机械式齿轮箱;文献[4]以滚刀节线和非圆齿轮节曲线保持纯滚动为依据,推导出非圆齿轮滚齿加工联动数学模型,并通过仿真进行了验证;文献[5]根据非圆齿轮滚齿加工模型,推导了工件转角误差和滚刀转角误差对非圆齿轮齿距影响的误差公式,但其计算过程过于复杂。因为齿轮加工涉及到多轴联动,所以存在多轴同步控制的问题[6]。文献[7]提出了一种简单的圆柱斜齿轮节距误差和螺旋线轮廓误差的估计方法,并结合这种估计方法提出一种电子齿轮箱交叉耦合控制器体系结构。
本文根据非圆齿轮滚齿加工数学模型,构建非圆齿轮滚齿加工电子齿轮箱运动控制模型,并从几何角度分析推导电子齿轮箱展成控制误差所引起的非圆齿轮齿距误差;建立电子齿轮箱非圆齿轮齿距误差补偿控制器,并把齿距误差补偿控制器添加到电子齿轮箱运动控制模型中,通过仿真实验分析对比补偿前、后的控制效果。
1 非圆齿轮运动控制模型
1.1 非圆齿轮滚齿加工数学模型
沿滚刀轴线做剖切面,滚刀加工非圆齿轮可以看作齿条刀具加工非圆齿轮,如图1所示。

图1 非圆齿轮滚齿加工端面图
图1中:点P为齿条中线与非圆齿轮节曲线相切点;r为对应极径;μ为极切角;ωB为滚刀转速;ωC为齿坯转速。
由几何关系可知,非圆齿轮节曲线与刀具齿条切点处的速度在X方向和Y方向的分量为:
vX=rωBcosμ
(1)
vY=rωCsinμ
(2)
滚刀的回转除形成切削速度外,还可形成投影工具齿条在法面内的移动速度,此速度由滚刀回转实现,即
(3)
其中:k为滚刀头数;m为非圆齿轮端面模数;β为非圆齿坯螺旋角。
由(2)式和(3)式得非圆齿坯展成速度为:
(4)
为了形成工具斜齿条,刀具齿条和工件在法平面内要有相对速度Δvn。当滚刀以速度vZ沿齿坯轴向运动时,由啮合点处滚刀与齿坯的法向速度相等可得:
Δvn=vZsinβ
(5)
为补偿Δvn,令工件的附加转速为ΔωC,有:
Δvn=rΔωCsinμcosβ
(6)
由(5)式和(6)式得到工件的附加转速为:
(7)
由(4)式和(7)式得到的工件最终转速为:
(8)
由(1)式和(4)式可得滚刀与齿坯之间的径向进给速度为:
(9)
综上所述,非圆齿轮滚齿加工运动模型为:
vZ=kZ
(10)
其中:kZ为常数;当β=0时,表示加工非圆直齿轮;滚刀螺旋升角与工件齿轮螺旋角的旋向相同时取“+”,旋向相反时取“-”。
1.2 非圆齿轮电子齿轮箱运动控制模型
电子齿轮箱按结构可以分为主从式结构和平行式结构。主从式电子齿轮箱是从动轴对主动轴的跟随控制,主动轴转速经编码器检测后传递到电子齿轮箱模块,作为从动轴的控制信号。平行式电子齿轮箱是对每个运动轴进行独立控制,但如果其中一个轴受到干扰,就不能很好地与其他轴保持同步运动。而主从式结构在主动轴受到干扰的情况下,从动轴能够跟踪主动轴的变化[8],因此本文采用主从式的电子齿轮箱结构。
对于非圆齿轮滚齿加工,在加工过程中参与运动的轴有4个,分别为滚刀轴B轴、齿坯旋转轴C轴、相对齿坯径向往复运动的径向进给轴X轴和为滚切出全齿宽的轴向运动轴Z轴。在切削加工时,一般滚刀轴B轴给予恒定转速,当伺服电机编码器采集到B轴转速后作为基准信号传递给处理器,经过电子齿轮箱模块转换为从动轴X轴的控制信号,从动轴C轴的控制信号由B轴和Z轴的控制信号共同经过电子齿轮箱模块转化得到。
建立主从式非圆齿轮滚齿加工电子齿轮箱结构,如图2所示。
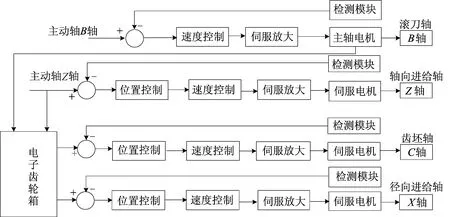
图2 非圆齿轮滚齿加工电子齿轮箱结构图
2 非圆齿轮齿距误差数学模型
非圆齿轮误差是类比圆柱齿轮的误差项来定义[9]的,分为齿距误差、齿廓误差、齿向误差等。本文主要研究在非圆齿轮加工中,电子齿轮箱展成控制误差导致的非圆齿轮齿距误差。齿距误差为在非圆齿轮节曲线上实际齿距与理论齿距之差,其反映的是一齿内的转角误差,主要对齿轮工作时的准确性产生影响。
对于非圆齿轮滚齿加工,首先考虑从动轴径向进给轴X轴运动误差对齿距的影响,具体如图3所示。

图3 X轴运动误差对齿距的影响
图3b中,EX为径向进给轴X轴的位置跟踪误差,其对非圆齿轮齿距的影响为在节曲线切线上的分量EX′。由几何关系可得:
EX′=EXtanβ
(11)
其中,β=μ-90°,μ为极切角。
其次考虑齿坯轴C轴转角误差对最终加工的非圆齿轮齿距的影响,如图4所示。

图4 C轴的跟踪误差对非圆齿轮齿距的影响
图4b中,EC为非圆齿坯轴C轴的位置跟踪误差,其对非圆齿轮齿距的影响为在节曲线上的弧长EC′。由几何关系可得:
EC′=rEC
(12)
其中,r为非圆齿轮啮合点处的极径。
根据(11)式和(12)式可得滚刀径向进给轴X轴的跟踪误差和齿坯轴C轴跟踪误差对非圆齿轮齿距的影响Fp,即
Fp=EX′+EC′=EXtanβ+rEC
(13)
3 非圆齿轮齿距误差补偿仿真模型
3.1 非圆齿轮齿距误差补偿控制数学模型
根据推导的非圆齿轮加工中齿距误差公式,构建非圆齿轮齿距误差补偿控制数学模型。
将齿距误差数学模型重写如下:
Fp=EX′+EC′=EXtanβ+rEC
(14)
其中:EX为X轴位置跟踪误差;EC为C轴位置跟踪误差;r为非圆齿坯节曲线极径。
为了减小或者消除X轴和C轴运动误差导致的齿距误差,一种方法是对齿坯轴C轴补偿相应的量ΔEC,即令:
Fp=EXtanβ+r(EC+ΔEC)=0
(15)
有
(16)
简化为:
ΔEC=kXEX+kCEC
(17)
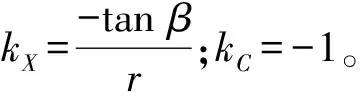
另一种方法是对X轴引入补偿量ΔEX,使齿距误差为0,即
Fp=(EX+ΔEX)tanβ+rEC=0
(18)
同理可得:
ΔEX=kCEC+kXEX
(19)
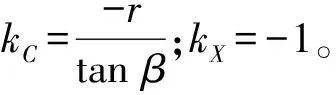
由(19)式可知,因为正切函数位于分母位置,导致补偿量ΔEX变动特别大,会引起X轴的位置波动较大,所以本文只针对C轴进行补偿控制。
3.2 电子齿轮箱控制误差补偿仿真模型
根据文献[10]建立伺服控制系统模型,如图5所示。

图5 伺服控制系统模型
图5中:Ka为电流环增益;Kt为电机转矩系数;J、B分别为电机轴等效转动惯量和等效摩擦黏性系数;u为输入电压信号;Tm为驱动转矩;Tf为干扰转矩;ω为电机转速。
以非圆直齿轮滚齿加工电子齿轮箱仿真为例,建立滚刀轴B轴、齿坯轴C轴和径向进给轴X轴三轴联动模型,以B轴为主动轴,C轴和X轴为从动轴。根据构建的非圆齿轮滚齿加工电子齿轮箱结构图以及非圆齿轮齿距误差补偿控制数学模型,在MATLAB/Simulink环境中建立非圆齿轮滚齿加工电子齿轮箱齿距误差补偿控制仿真模型,如图6所示。
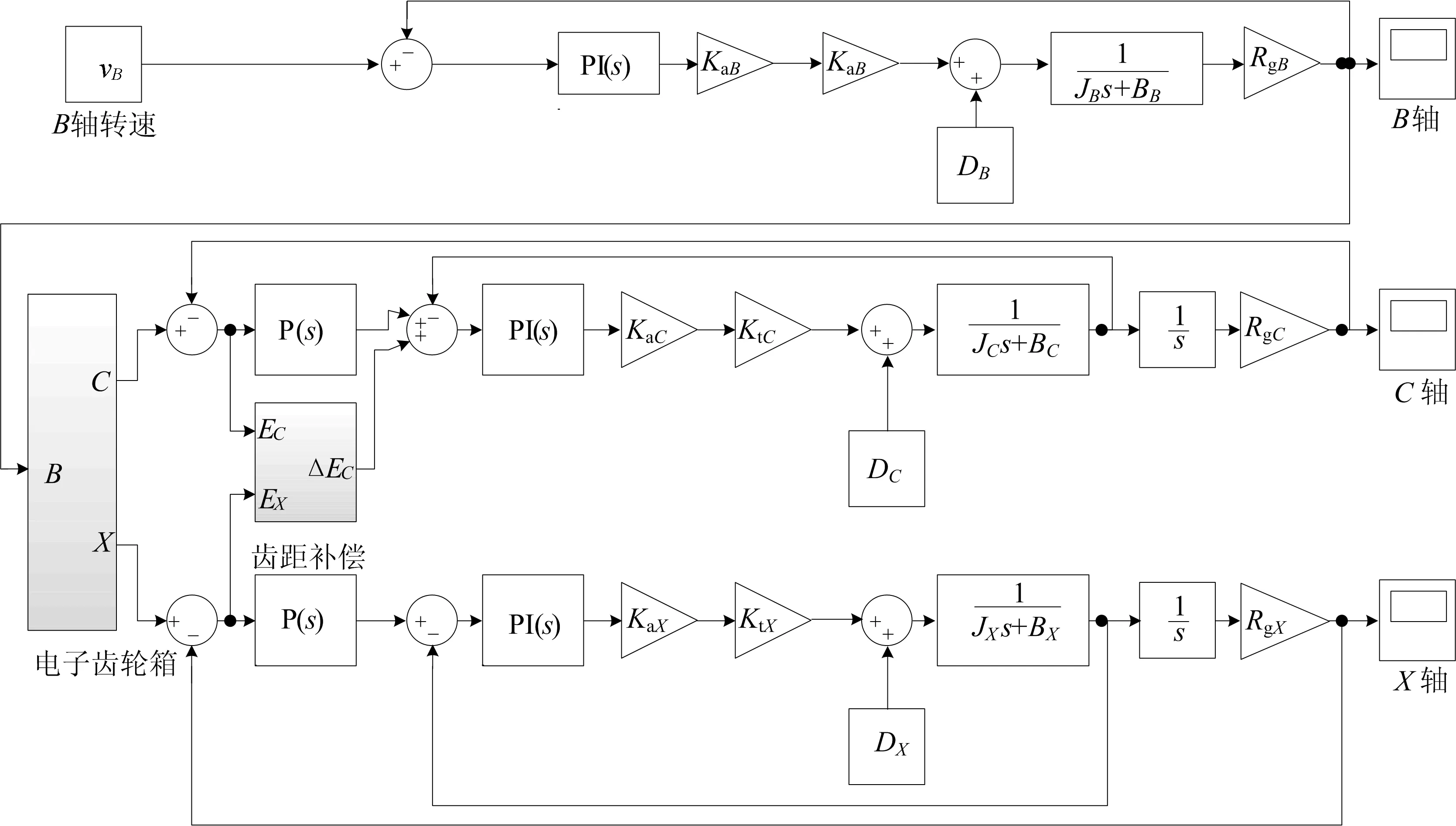
图6 非圆齿轮滚齿加工电子齿轮箱齿距误差补偿控制仿真模型
图6中:KaB、KaC、KaX为各轴电流环增益;KtB、KtC、KtX为各轴电机转矩常数;JB、JC、JX为各轴等效惯量;BB、BC、BX为各轴等效黏性阻尼系数;DB、DC、DX为各轴干扰信号;RgB、RgC、RgX为各轴速度或位移转换系数。
本文中,B轴采用速度控制方式,C轴和X轴分别采用位置环和速度环双环控制方式,速度环采用比例积分PI控制器,位置环采用比例P控制器。
以滚切二阶椭圆齿轮为例,其节曲线方程可为:
(20)
其中:a为长半轴,取26.48 mm;e为偏心率,取0.2;n为阶数,取2。
选取各轴相关电机参数[11],见表1所列。

表1 电子齿轮箱运动轴仿真参数
根据图6建立的仿真模型及表1设定好的相应参数,考虑到实际加工非圆齿轮滚刀转速较低,令主轴B转速为100 r/min,在Simulink环境下进行仿真实验,并设定运行采样周期为1 ms,分别得到补偿前、后位置跟踪误差和齿距误差,如图7、图8所示。
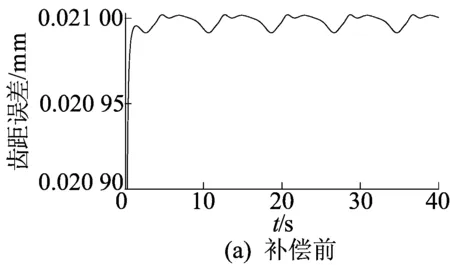
图8 补偿前、后齿距误差的对比
补偿前、后电子齿轮箱控制性能对比见表2所列。

表2 补偿前、后电子齿轮箱控制性能对比
从图7可以看出,补偿后的C轴跟踪误差明显减小,而补偿后的X轴位置跟踪误差没有变化。这是因为仿真实验只是对C轴进行补偿来降低齿距误差,所以对X轴的控制性能没有造成影响。
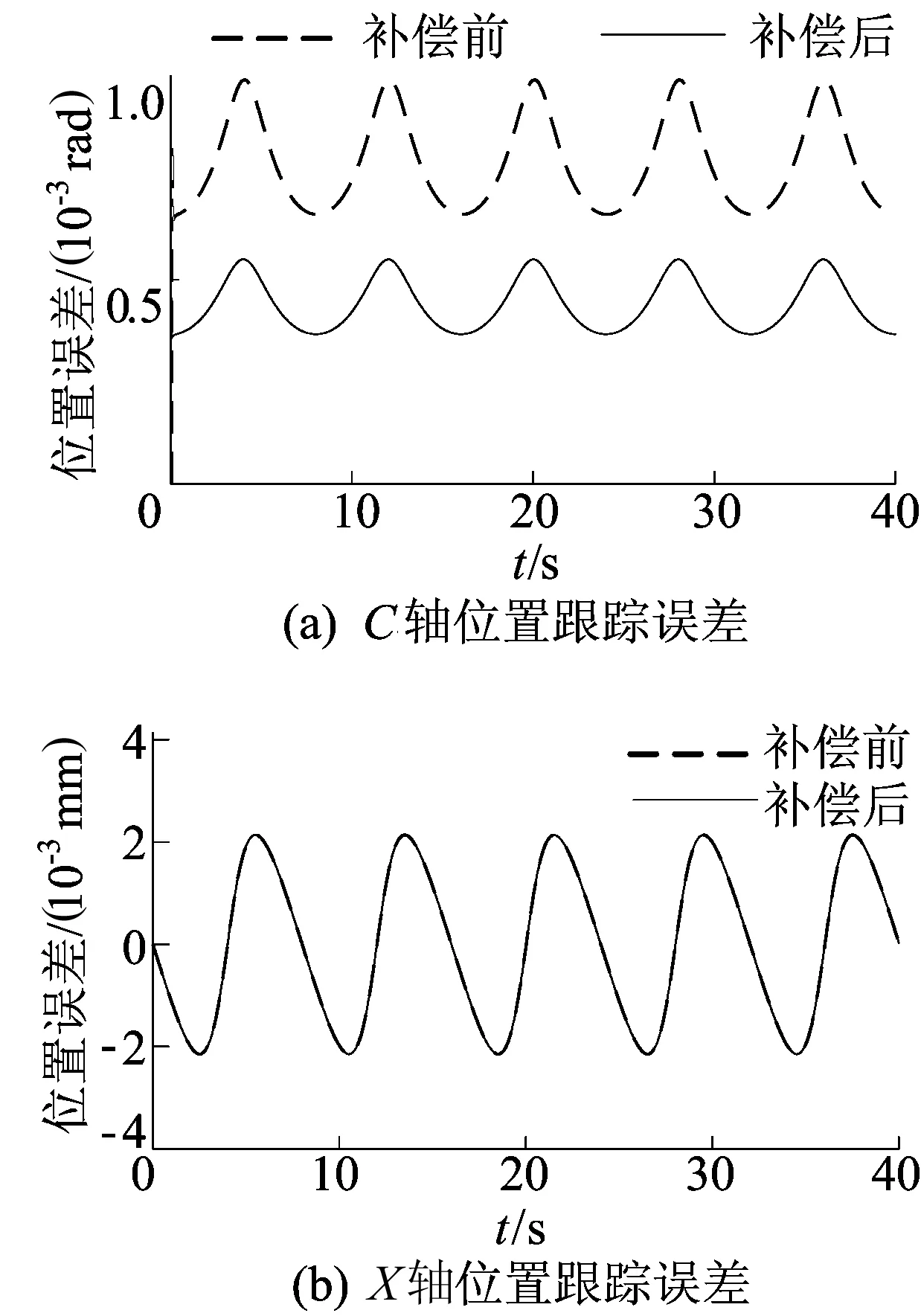
图7 补偿前、后C轴和X轴位置跟踪误差的对比
从表2可以看出,补偿后齿距误差的最大值由0.026 57 mm降到0.016 03 mm,平均值由0.020 99 mm降到0.011 66 mm。
4 结 论
(1)本文根据非圆齿轮滚齿加工数学模型,构建了非圆齿轮滚齿加工电子齿轮箱运动控制模型,并从几何角度分析推导了电子齿轮箱展成控制误差所引起的非圆齿轮齿距误差。
(2)根据构建的非圆齿轮齿距误差关系式,建立电子齿轮箱非圆齿轮齿距误差补偿控制器,并将其添加到电子齿轮箱运动控制模型中,构建出非圆齿轮滚齿加工电子齿轮箱齿距误差补偿控制仿真模型。
(3)研究结果表明,补偿后的非圆齿轮的齿距误差降为补偿前的60.33%,补偿后的非圆齿轮的齿距误差平均值降为补偿前的55.56%。同时也提升了从动轴C轴的跟踪精度,由于只对C轴进行补偿来降低齿距误差,对X轴的控制性能没有造成影响。
